Hilbert空間上兩個冪等算子組合的Drazin逆

周建新， 汪金漢，陳敬華

(湖北師范學院 數學與統計學院， 湖北 黃石 435002)

Hilbert空間上兩個冪等算子組合的Drazin逆

周建新， 汪金漢，陳敬華

(湖北師范學院 數學與統計學院， 湖北 黃石 435002)

討論了Hilbert空間上的兩個不同的冪等算子P、Q的組合aP+bQ-cPQ的Drazin可逆性問題，利用冪等算子的性質和空間分解的技巧證明了aP+bQ-cPQ的Drazin逆在條件PQP=0 下是存在的，并且給出了其逆的計算公式，其中a,b,c∈,ab≠0 .

冪等算子；Drazin逆；冪等算子的組合

0 引言

設H是一個復數域上的Hilbert空間，Γ(H)表示H上的所有有界線性算子構成的集合. 若P∈Γ(H)且滿足P2=P，則稱P是一個冪等算子. 若P∈Γ(H) 且滿足P2=P=P*，則稱P是一個正交冪等算子，其中P*是P的共軛元. 用P(H)表示Γ(H)中所有冪等算子構成的集合，則P(H)在相似變換下保持不變，即若P∈P(H)，則對任意的可逆算子S∈Γ(H)，都有S-1PS∈P(H) .

若對于A∈Γ(H) ，存在B∈Γ(H) 使得

BAB=B,AB=BA,Ak+1B=Ak

(1)

都成立，其中k是非負整數，則稱B是A的一個Drazin逆. 若A∈Γ(H) 存在Drazin逆，則其Drazin逆一定是唯一的，記為AD，并且稱使得(1)成立的最小的非負整數k為A的指數，記為 ind(A). 容易證明：當 ind(A)=0時，A為通常的可逆算子，此時AD=A-1；當 ind(A)≤1，A是群逆存在的[1]. 關于算子廣義逆的基礎知識可參考文獻[1～2]. 文獻[2]證明了A的Drazin逆存在的充要條件是ind(A)<∞，此時0是預解算子Rλ=(λI-I)-1的有限階極點. 另外，Γ(H)中算子的Drazin逆也具有相似不變性，即如果A是Drazin可逆，S∈Γ(H) 是任意的可逆算子，則S-1AS仍Drazin可逆，并且(S-1AS)D=S-1ADS.

Drazin逆的概念最早由Drazin于1958年在他的一篇論文中提出[3]，隨后發現在許多其它的應用數學分支中有重要的應用，可見文獻[1，2，4～8] 在文獻[3]中，Drazin首先考慮了當P和Q是兩個冪等算子時，(P+Q)D的存在性問題，他證明了：若PQ=QP=0，則(P+Q)D存在，且(P+Q)D=PD+QD. 在不添加其它的條件下探討(P+Q)D的存在性并且將其表示成P，Q，PD，QD的函數是一個非常困難的問題，而且至今仍是一個公開問題[9].

文獻[4]分別在三個條件：(i)PQP=0；(ii)PQP=P；(iii)PQP=PQ下探討了P+Q的Drazin逆的存在性及其計算公式.

文獻[10]考慮了復數域上一個特殊的組合aP+bQ-cPQ，其中P,Q是復數域上的非零冪等矩陣，a,b,c是復數且a,b≠0，則

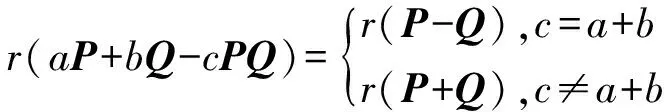
其中r(A) 表示矩陣A的秩.隨后，文獻[11]發現：只要ab≠0 且a+b+c≠0，aP+bQ+cPQ的Fredholm性、零度、指數與系數a,b,c的選取無關.

文獻[13]在上述的三個條件下討論了Banach空間上兩個冪等元的線性組合的Drazin逆的存在性、Drazin逆的表達式及指數.

設P，Q是Hilbert空間上兩個不同的冪等算子，受到上述工作的啟發，我們利用冪等算子的性質和空間分解的技巧證明了aP+bQ-cPQ的Drazin逆在條件PQP=0 下是存在的，并且給出了其逆的計算公式，其中a,b,c∈,ab≠0 .

1 預備引理

為了證明本文的主要結果，我們需要以下引理：

引理1[8]設A，B,C∈Γ(H),若A,B是Drazin可逆的， 則

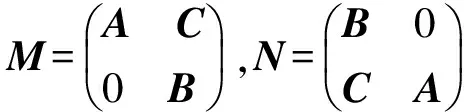
也是Drazin可逆的并且

當引理1中的A是可逆的且B是冪零的，則M的Drazin逆有如下結論：

引理2[8]設A,B,C∈Γ(H)，若A,B是Drazin可逆的， 若A是可逆的且存在正整數k使得Bk=0，則

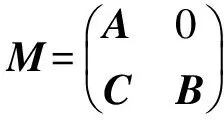
是Drazin可逆的并且

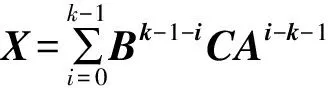
對于算子A∈Γ(H) ，用R(A) 表示A的值域，N(A) 表示A的核空間，則Γ(H) 上的任意兩個算子值域的包含關系與它們的運算之間有如下結果：

引理 3[11]設A,B∈Γ(H)，則以下兩條等價

(i)R(B)?R(A)；

(ii)存在D∈Γ(H)，使得B=AD.

2 主要結果及證明

設P，Q是Hilbert空間上兩個不同的冪等算子，本節將利用冪等算子的性質和空間分解的技巧證明aP+bQ-cPQ的Drazin逆在條件PQP=0 下是存在的，并且給出了其逆的計算公式，其中a,b,c∈,ab≠0.

定理1 設P，Q∈P(H)，a,b,c∈且ab≠0. 若PQP=0，則aP+bQ-cPQ的Drazin逆是存在的，且

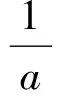
證 設P,Q∈P(H)，則組合aP+bQ-cPQ是Drazin可逆的當且僅當

aS-1PS+bS-1QS-c(S-1PS)(S-1QS)

是Drazin可逆的，其中S∈Γ(H) 是任意的可逆算子. 因此不失一般性，可以設P是正交冪等算子.

由引理 3 及條件PQP=0 可知R(QP)?N(P) 和R(QP)?R(Q) 成立. 注意到

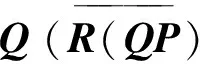
則有如下的空間分解

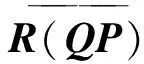
另外，因為Q是冪等算子，所以由Q2=Q可得

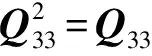
則，H可進一步分解為

在上述空間分解下，算子P,Q的矩陣形式進一步可以表成

由Q2=Q可知

對于a,b,c∈，且ab≠0，算子P,Q的組合aP+bQ+cPQ有如下的矩陣形式

注意到ab≠0 意味著上述矩陣的子矩陣

另外，

由引理2中令B=0，則

這樣就證明了aP+bQ+cPQ在條件PQP=0下的Drazin逆是存在的. 下面將其表成P，Q，PQ，QP，QPQ的組合(由于PQP=0，aP+bQ+cPQ只能由這些算子線性表出).

經過計算可得

從而通過求解方程組，可求出表出系數，得到aP+bQ+cPQ的Drazin逆為

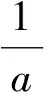
由定理1， 令a=1,b=1,c=0 與a=1,b=-1,c=0 則可以得到兩個冪等算子P，Q和與差的Drazin逆在條件PQP=0下是存在的，且其表達式也可以給出.

推論1[13]設P,Q∈P(H)，則以下兩條成立：

1)(P+Q)D=P+Q-2(PQ+QP)+3QPQ.

2)(P-Q)D=P-Q-QPQ.

由于條件PQ=0 或者QP=0 能夠推出PQP=0，于是可得如下結論：

推論2 設P,Q∈P(H) ，則以下兩條成立：

1)若QP=0，則對于任意的a,b∈，a,b≠0有 (aP+bQ)D=P+Q-(+)PQ.

2)若PQ=0，則對于任意的a,b∈，a,b≠0有 (aP+bQ)D=P+Q-(+)QP.

[1]Wang Guorong, Wei Yiming, QIAO S. Generalized inverse: theory and computations[M]. Graduates Series in Mathematics, Beijing: Science Press, 2004.

[2]Campbell S L, Meyer C D. Generalized inverse of linear transformations[M]. London: Pitman Press, 1979.

[3]Drazin M P. Pseudo inverse in associative rings and semigroups[J]. American Mathematical Monthly, 1958,65:506～514.

[4]Djordjrvic D S, Stanimirovic P S. On the generalized Drazin inverse and generalized resolvent[J]. Czechoslovak Mathematical Journal, 2001, 126:617～634.

[5]Douglas R G. On majorization factorization and range inclusion of operators in Hilbert space[J]. Proceedings of the American Mathematical Society, 1966, 17: 413～416.

[6]Hartwig R E, Levine J. Applications of the Drazin inverse to the Hill cryptographic system[J]. Crytologia, 1981, 5:67～77.

[7]Meyer C D. The condition number of a finite Markov chains and perturbation bounds for the limiting probabilities[J]. SIMA Journal on Algebraic Discrete Methods, 1980, 1:273～283.

[8]Simeon B, Fuhrer C, Rentrop P. The Drazin inverse in multibody system dynamics[J]. Numerische Mathematik, 1993, 64:521～536.

[9]Hartwig R E, Wang Guorong, Wei Yiming. Some additive results on the Drazin inverse[J]. Linear Algebra and its Applications, 2001, 322:207～217.

[10]Zuo Kezheng. Nonsingularity of the difference and the sum of two idempotent matrices[J]. Linear Algebra and its Applications, 2010, 433:476～482.

[11]Xie Tao, Zuo Kezheng. Fredholmness of combinations of two idempotents[J]. European Journal of Pure and Applied Mathematics, 2010, 3(4):678～685.

[12]Liu Xiaoji, Wu Lingling, Yu Yaoming.The group inverse of the combinations of two idempotent matrices[J], Linear and Multilinear Algebra, 2011:59:101～115.

[13]Deng Chunyuan. The Drazin inverses of sum and difference of idempotents[J]. Linear Algebra and its Applications, 2009, 430:1282～1291.

TheDrazininvertibilityofcombinationsoftwoidempotentoperatorsoveraHilbertspace

ZHOU Jian-xin, WANG Jin-han, CHEN Jing-hua

(College of Mathematical and Stastical, Hubei Normal University, Huangshi 435002, China)

Discussed the problem of Drazin invertibility of combinations of two idempotent operatorsP、Qon a Hilbert space. By using the properties of idempotent operators and the techniques of space decomposition, prove the existance of Drazin invertibility of the combinationsaP+bQ-cPQand its expression is also obtained, wherea,b,c∈,ab≠0.

Idempotent operator; Drazin invertibility; combinations of idempotent operators

2014-02-22；

湖北省教育廳重點項目(D20122202)，湖北省教育廳青年項目(B20122203)

周建新(1955— )，男，湖北黃石人，研究方向為數學教育.

O177.2

A

1009-2714(2014)02- 0023- 05

10.3969/j.issn.1009-2714.2014.02.006