雙粗糙面滑動摩擦熱力耦合有限元分析

駱華榮，高誠輝

(福州大學 機械工程及自動化學院，福建 福州 350108)

0 前言

工程表面微觀上是凹凸不平的，在摩擦副的運動過程中，實際接觸只發生在少數較高微凸體上。這些實際接觸的微凸體承受了很大的載荷而產生變形，并產生摩擦熱而引起較大溫升，造成局部膨脹，使接觸壓力不均勻分布，進一步加劇微凸體的變形[1]。這些局部受力和受熱微凸體的出現導致工程表面產生磨損，甚至破壞，嚴重影響了摩擦副的正常運轉。因此，實時分析摩擦副滑動過程中溫度場、應力場及磨損的變化規律對于研究摩擦與磨損的物理本質、摩擦副表面性質的變化、摩擦磨損的微觀熱動力學行為和磨損破壞機制是十分必要和有效的。而摩擦磨損發生在相互運動的摩擦副粗糙表面間，難以進行動態觀察和檢測。隨著計算機技術的發展，為了深入分析摩擦副滑動摩擦接觸熱動力學分布狀況及特點，常采用有限元法進行仿真研究。

Jaeger[2]很早就對在半空間體上的移動熱源產生的溫升提出了一個最完整解。Bhushan[3,4]針對多點微凸體接觸，提出了一套詳細的熱傳導方法來計算微凸體接觸過程中的溫升，并分析了多個微凸體的累積效應。而Johansson和Klarbring[5]較早使用有限元法對熱接觸問題進行了系統研究，并給出了熱接觸問題模型的數學描述。Gao J-Q等[6]則提出了一種計算粗糙表面瞬時閃溫的模型，使用快速傅里葉變換技術，計算了粗糙表面接觸瞬時閃溫，并得到了接觸壓力分布。Liu S-B和Liu G等[7-9]為了計算方便，將三維接觸問題簡化為一個具有等效材料特性的粗糙半空間和一個球體的接觸，使用快速傅里葉變換和共軛梯度法，通過有限元方法，計算了在穩態熱傳遞情況下微凸體上由接觸壓力、切向摩擦力、摩擦熱引起的位移。而對熱力耦合模型的計算，Cho和Komvopoulos[10]提出了用于計算亞表層裂紋擴展的熱力耦合有限元模型。Gong和Komvopoulos[11,12]則在考慮熱力完全耦合的情況下，建立了彈塑性平面與球體之間的有限元分析模型以及彈性半無限體與剛性粗糙實體間相對滑動的計算模型。文獻[13,14]基于G-W(Greenwood-Williamson)接觸模型和W-M(Weierstrass-Mandelbrot)分形函數分別建立了三維熱力耦合有限元模型，將雙粗糙表面簡化為一粗糙表面與一理想平面，分析得到了粗糙表面溫度、應力等的分布規律。以上模型均為單粗糙表面與理想平面或球體接觸，未見摩擦副表面為雙粗糙面且考慮磨損的三維滑動摩擦接觸研究的報道。

本文在前期工作[15]的基礎上，采用熱力耦合有限元分析方法，著重考慮了滑動摩擦過程中熱傳遞及粘著磨損，基于W-M分形函數生成的粗糙表面，建立了彈塑性雙粗糙面滑動摩擦熱力耦合有限元模型，以Ti-6Al-4V合金的滑動摩擦為例，使用ABAQUS軟件，分析模擬了雙粗糙面滑動摩擦過程中的溫度場、應力場及磨損情況。

1 熱力耦合計算模型的建立

1.1 接觸模型的建立

采用W-M分形函數生成粗糙表面，選擇具有代表性的分形粗糙表面局部，建立雙粗糙面接觸模型。如圖1所示，A、B分別表示摩擦副上、下粗糙實體。其中A1、B1分別表示摩擦副工作表面，A2、B2、A3、B3、A4、B4、A5、B5、A6、B6分別表示摩擦副非工作表面(圖中括號里的面為可見面的正對面)，hA、hB分別表示粗糙實體A、B的厚度，lA、lB分別表示粗糙實體A、B的寬度，LA、LB分別表示粗糙實體A、B的長度。

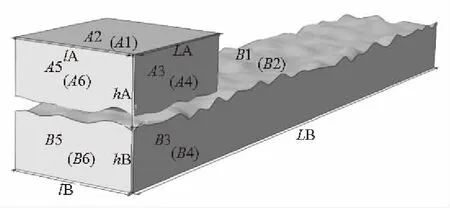
圖1 接觸分形幾何模型

1.2 熱分析模型的建立

在滑動摩擦過程中，摩擦副工作表面A1、B1產生摩擦熱，并以熱流的形式存在和輸入到摩擦副中。為了方便問題的分析及計算，作如下假設：

1) 摩擦副材料是各向同性的，且材料的密度、泊松比不隨溫度發生變化；

2) 只考慮粘著磨損的影響，且認為摩擦能量的絕大部分轉化為熱能；

3) 摩擦界面間的接觸熱阻極小，則接觸區域為理想熱傳導；

4) 摩擦熱流分配按摩擦副各自物理性質自動分配。

1.2.1 摩擦熱流密度的計算

在滑動過程中，大部分能量被直接轉化為摩擦熱，部分消耗于彈塑性變形能，則由摩擦熱引起的熱流密度q(x,y,t)為：

q(x,y,t)=η×μ×p(x,y,t)×ν(x,y,t)

(1)

式中：μ——摩擦系數；p(x,y,t)——摩擦界面上的比壓；v(x,y,t)——摩擦副間的相對滑動速度；η——摩擦能量轉化為熱流密度的比例系數，假設有90%能量轉化為熱能，即取η=0.9。

1.2.2 熱傳導方程

根據Fourier傳熱定律和能量守恒定律，基于材料的各向同性，粗糙實體A、B的熱傳導控制方程為：

(2)

式中：ρA、ρB——粗糙實體A、B的材料密度；cA，cB——粗糙實體A，B的材料比熱容；kA，kB——粗糙實體A，B的材料導熱系數；TA，TB——粗糙實體A，B的溫度；t——滑動時間。

1.2.3 熱邊界分析

摩擦副工作表面A1、B1在相互接觸的摩擦區域有摩擦熱流的輸入及摩擦界面之間的熱傳導；粘著磨損產生新表面、形成磨屑所消耗的能量；在非接觸區域存在與空氣的對流換熱和熱輻射。

文中的接觸模型是從宏觀物體上截取的微觀粗糙實體，摩擦副的非接觸表面是與各自的其余部分材料相連在一起的，存在著材料本身的熱傳導，但由于微區間相對宏觀表面來說較小，滑動的時間又極短，溫度變化較小，故假設摩擦副的非工作表面為絕熱表面。

1.3 熱力耦合計算分析

滑動過程中產生的摩擦熱會導致摩擦界面的接觸狀態發生改變，即接觸面上的壓力會隨時間變化，而壓力的變化會反過來影響界面上的摩擦熱流分布。因此，滑動摩擦過程是一個典型的熱力耦合問題，溫度場和壓力場之間的關系可由式(1)得到。本文采用熱結構順序耦合方法進行計算分析，如圖2為熱力耦合過程框圖。具體步驟如下：

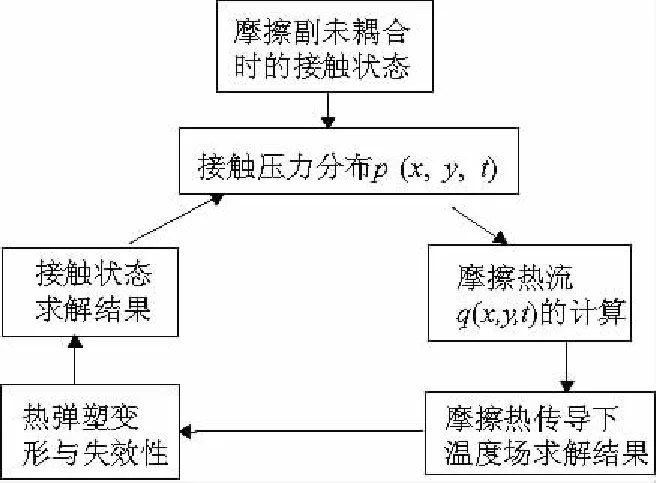
圖2 熱力耦合框圖

1) 根據初始條件設定一接觸狀態，獲取界面壓力分布p(x,y,t)；

2) 由接觸壓力計算界面上的摩擦熱流密度q(x,y,t)；

3) 將摩擦熱流輸入摩擦副求解溫度場{T}；

4) 求解由溫度場引起的應變增量；

5) 求解摩擦副的溫度載荷增量，并與機械載荷疊加得到綜合載荷，求解熱彈塑性變形與材料失效產生的粘著磨損；

6) 判斷接觸狀態是否與設定狀態一致，若不一致，則將所求得的接觸狀態作為下一輪計算的設定接觸狀態，重復(2～5)步驟；若一致，則求得的接觸狀態正確，進行下一增量步的計算；依此類推，直至滑動過程結束。

1.4 失效準則分析

雙粗糙面上的微凸體相嵌接觸，要實現摩擦副的連續滑動，就必須考慮材料的損傷失效，文中采用Johnson-Cook Damage準則[16]來定義材料的動態失效。該準則是基于單元積分點處等效塑性應變的值，當損傷參數D的值超過1時，則假定磨損發生，即認為該單元失效，在隨后的滑動摩擦中該單元被刪除，不再具有材料屬性及參與后續計算。損傷參數定義如下：

(3)

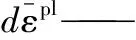
(4)

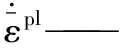
1.5 位移邊界條件的確定

假定粗糙實體A在受到法向均布載荷P的作用下沿x方向以速度v相對滑動，約束y方向位移；粗糙實體B固定不動，約束x，y，z方向位移。具體位移邊界條件如下：

摩擦副A：

摩擦副B：

2 實際算例

2.1 模型幾何參數

截取具有代表性的微粗糙實體，建立滑動摩擦接觸模型，選取模型幾何參數為：

LA=200μm，lA=185.66μm，hA=80μm；

LB=1020μm，lB=185.66μm，hB=84μm。

2.2 材料屬性

配副材料選用具有強度高、質量輕、耐熱性強、耐腐蝕性好等特點的Ti-6Al-4V合金，它常用于航空航天、軍事、生物醫學和汽車等領域。具體性能參數如表1所示[17]。

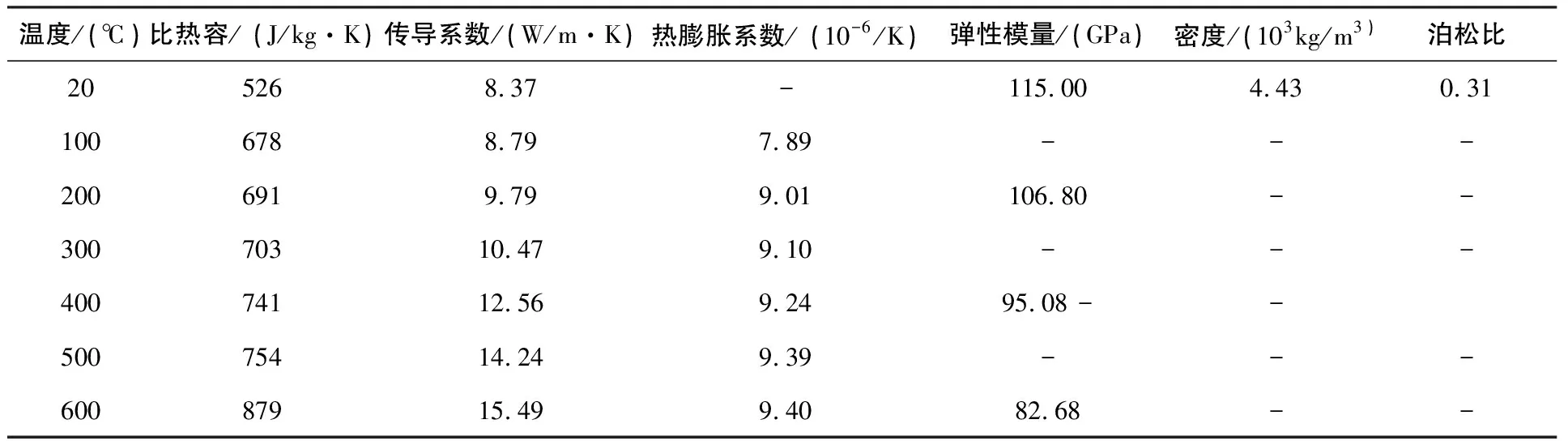
表1 Ti-6Al-4V的材料性能

采用DCS-200型微機控制電子萬能實驗機對Ti-6Al-4V合金進行試驗，經適當簡化后得到圖3所示的具有累積損傷的應力-應變曲線。

3 計算結果及分析

3.1 摩擦界面的最高接觸溫度

摩擦熱產生的溫升會導致材料的力學性能及摩擦條件退化，從而對其摩擦學行為產生重要影響，其中最高接觸溫度是其重要表征。圖4為摩擦界面最高接觸溫度隨(t=0～2.5μs)，由于摩擦副為彈塑時間的變化曲線。模型在未滑動的法向接觸階段性材料，少數微凸體對發生塑性變形，塑性變形能轉化為熱能而使摩擦界面溫度略有升高。

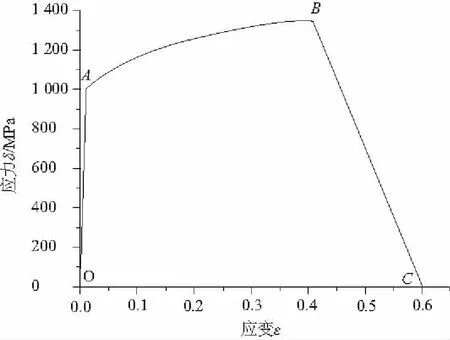
圖3 Ti-6Al-4V合金具有累積損傷的應力-應變曲線

圖4 界面最高溫度隨時間的變化曲線

在滑動的初始階段(t=2.5～7.5μs)，隨著相對滑動速度的迅速增大，輸入界面微小接觸區域的摩擦熱流相應增多，摩擦界面接觸溫度急劇上升，且由于微凸體的相互作用，導致在摩擦界面出現溫度很高的閃溫，并在滑動過程中隨時都在變化，最高可達近900℃；同時滑動過程中材料磨損形成的磨屑消耗了部分熱能，以及摩擦界面存在熱傳導、與空氣的熱對流和熱輻射效應，使界面最高接觸溫度在此階段具有較大波動。在隨后的勻速滑動階段(t=7.5～25.5μs)，由于磨損量不斷增加，消耗了摩擦界面大量熱能，加上熱傳遞效應的散熱作用，使界面最高接觸溫度大幅下降并出現波動。

滑動過程中出現閃溫的主要原因是摩擦副表面微凸體高低不平，實際接觸只發生在少數微凸體上，其中幾個較高的微凸體在外載荷的作用下發生較大的擠壓變形，產生較高的接觸壓力，滑動所產生的摩擦熱在這些微凸體接觸點上體現，并由于熱傳遞的滯后性，使表面局部產生很高的接觸溫度；而在勻速滑動階段后期，由于較高微凸體被磨損，表面被逐漸磨平，受較高微凸體的影響逐漸減小，摩擦界面未出現很高的接觸閃溫

3.2 摩擦副的應力分析

滑動摩擦過程中，摩擦副接觸區域的應力場分布對摩擦副的摩擦磨損有很大的影響，尤其是與相對滑動速度平行的應力分量σxx的大小和分布對摩擦副的磨損起著決定性的作用。

圖5為不同時刻的粗糙實體A工作表面Von Mises等效應力場分布圖。由圖可知，由于摩擦副表面是凹凸不平的，加載初始法向均布載荷較小，實際接觸只發生在少數幾個不連續的較高微凸體上，Von Mises等效應力場分布主要在其周圍(圖5a)。而后隨法向均布載荷的增加，應力不斷增大，法向均布載荷達到最大時(t=2.5μs)，Von Mises等效應力場分布區域明顯增大，Von Mises等效應力超過材料的屈服強度，發生塑性變形，參與接觸的微凸體數逐漸增多(圖5b)。在隨后的初始滑動階段，由于法向壓力、切向滑動及溫升造成的熱應力的綜合作用，使摩擦副接觸區域Von Mises等效應力達到材料損傷時的應力而產生磨損，參與接觸的較高微凸體被磨損，接觸應力區域中心發生轉移，且數量也明顯增多，此時Von Mises等效應力場分布較為復雜(圖5c)。在后續勻速滑動階段，由于摩擦副的磨損及熱膨脹作用，表面接觸區域面積顯著增大，而外載荷保持不變，使得表面Von Mises等效應力略有下降(圖5d)。

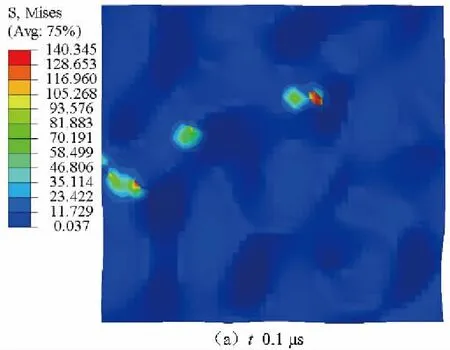
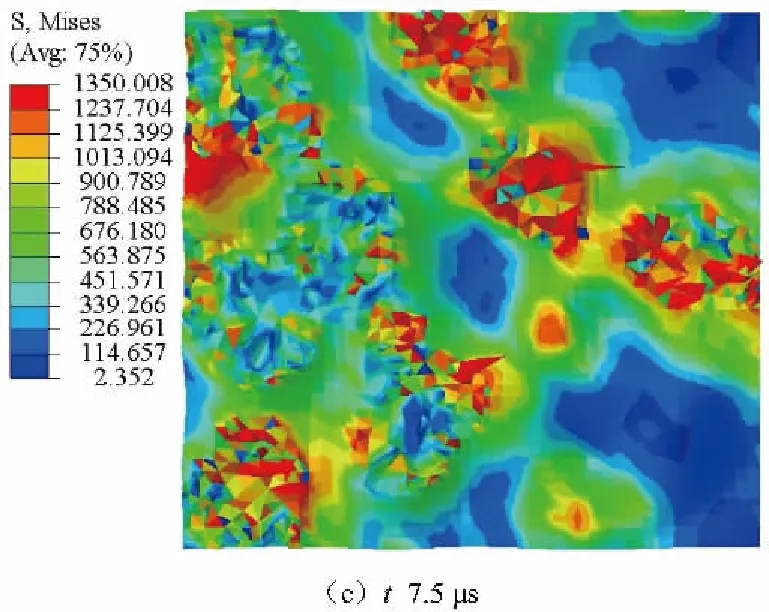
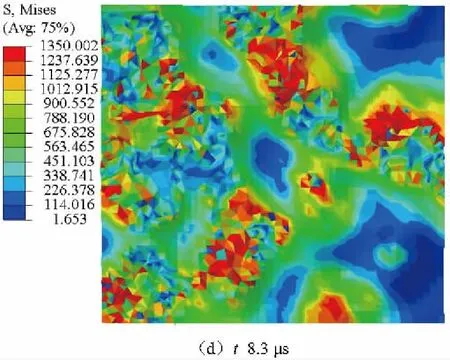
圖5 不同時刻摩擦表面Von Mises等效應力

圖6為在粗糙實體A的一較高接觸凸點(節點2504)下方4.15μm處節點8882所處剖面，其應力分量σxx在不同時刻沿深度方向的變化曲線。圖6中t=2.5μs,t=5μs,t=6.5μs分別表示摩擦副加載后滑動前，滑動后溫度上升，材料產生磨損的不同時刻。

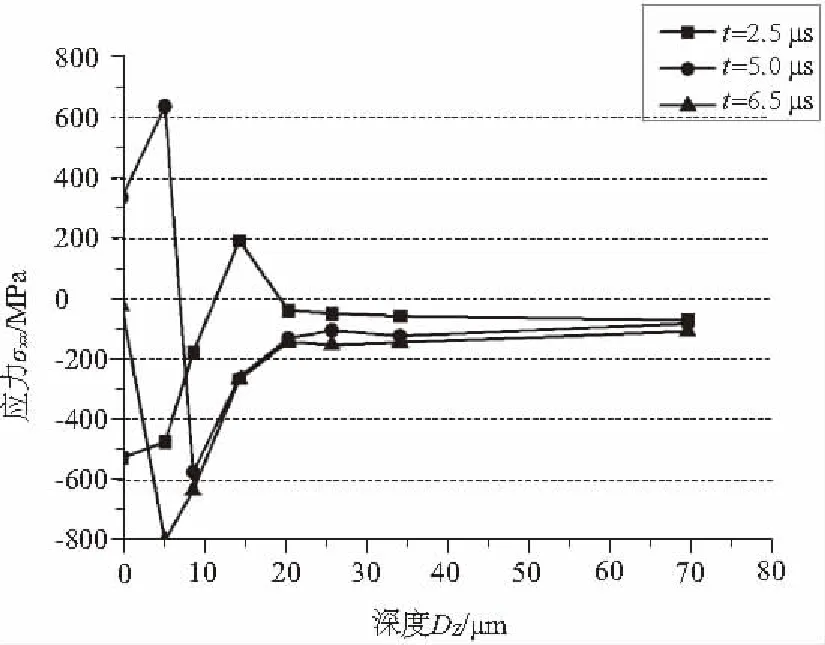
圖6 不同時刻應力σxx隨深度的變化曲線

從圖6中可以看出，在加載后滑動前(t=2.5μs)，接觸凸點下方大部分的σxx表現為壓應力，最大壓應力在表面上，隨深度增加逐漸減小以致改變應力方向變為拉應力，距表面15μm左右的深處拉應力最大。這是由于在外載荷的作用下，較高微凸體受壓發生彈塑性變形向外膨脹而表現為壓應力；而隨材料深度的不同，彈塑性變形程度也不同，故在接觸凸點下后方存在一拉應力區。

滑動后(t=5μs)隨著表面接觸溫度的急劇上升，在機械作用和熱應力的綜合作用下，摩擦副表層(0～5μm處)σxx由剛接觸時的壓應力區轉變為拉應力區，在隨后的滑動中，表面淺層材料在拉、壓應力的相互作用下逐漸形成裂紋，并在較大拉應力的作用下沿與相對滑動平行的方向延伸，從而導致材料脫落。摩擦副材料磨損后(t=6.5μs)被刪除，不再受應力作用，故被磨損的材料σxx值為零；而磨損后裸露出來的材料表面直接受到外載荷和熱應力的作用，使接觸區域材料σxx由t=5μs時的拉應力轉變為一較大的壓應力，后續沿材料深度方向上σxx在t=6.5μs與t=5μs時的分布幾乎相同，均表現為壓應力，但摩擦副除受機械作用外，還受熱應力作用的影響，因此，對應的壓應力數值比滑動前t=2.5μs時大。這一結果也表明，摩擦副滑動過程中，在表面下方一定深度處，將相繼受到壓縮-拉伸的循環應力作用[18]，從而形成裂紋并不斷擴展，產生磨損。

3.3 摩擦副磨損規律

本文采用磨損率對摩擦副的磨損情況進行分析。圖7為滑動過程中，摩擦副磨損率隨滑動距離的變化曲線。在滑動初始階段，開始滑動時的速度較低，外力對摩擦界面的切向作用力很小，剪切產生在摩擦界面，在一定的微小滑動距離內，未產生磨損，因而滑動初始磨損率為零；隨后由于滑動速度的增加，切向作用力增大，且此時摩擦界面溫度急劇升高，摩擦副表面受到重復性的機械和熱應力的綜合作用，剪切發生在離界面不遠處的材料內部，產生劇烈的磨損，從而使磨損率急劇增加。這一過程也說明摩擦磨損是同時受到正應力和切應力的作用，使接觸表面處于復雜的應力狀態而產生的。

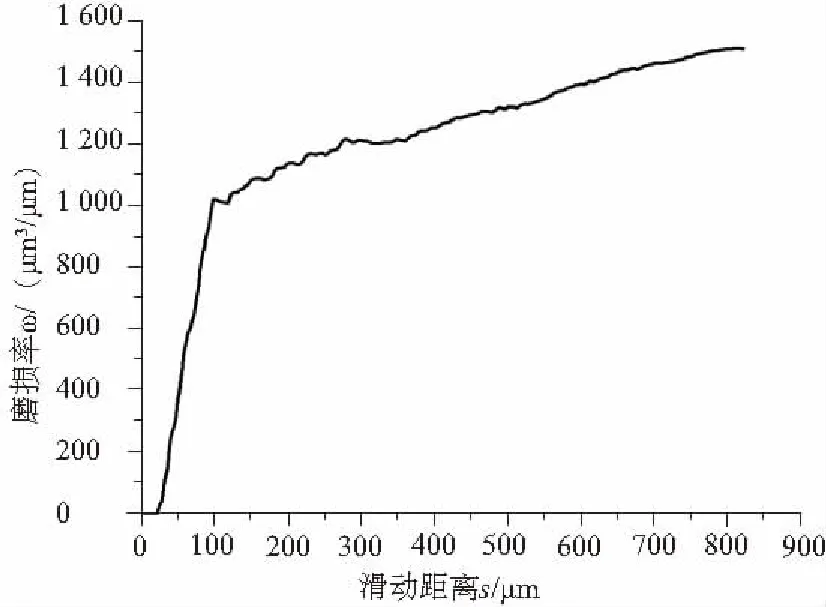
圖7 摩擦副磨損率隨滑動距離的變化曲線

當滑動距離超過100μm后，摩擦副進入勻速滑動階段，磨損率的增大比滑動初期大幅減緩，這是由于滑動速度不再增大，外載荷作用趨于穩定，單位滑動距離內的磨損體積增長速率反而減少；但在勻速滑動初期，仍存在較高接觸微凸體間的機械作用和熱應力作用，影響摩擦副的磨損，使磨損率會有微小波動，后隨著接觸峰點的磨損，表面形貌逐漸得到改善，磨損率趨于平緩。

4 結論

1) 加載階段，摩擦副材料發生塑性變形，界面溫度略有升高；滑動初始階段，滑動速度迅速增加，界面溫度急劇上升，最高可達900℃。由于磨損及熱傳遞效應的存在，溫升過程中有較大波動；勻速滑動階段，磨損消耗了大量熱能，加上傳熱及散熱的影響，界面最高接觸溫度大幅下降并存在波動；而在較高微凸體間的相互作用下，導致界面出現溫度很高的閃溫。

2) 滑動過程中隨著表面接觸區域面積的增大，Von Mises等效應力略有下降；而應力分量σxx在不同時刻隨深度的不同表現為壓應力和拉應力，且在摩擦副表層拉、壓應力之間相互轉變，材料的磨損正是受到壓縮-拉伸循環應力的作用而產生的。

3) 滑動初始階段，滑動速度低，切向作用力很小，未產生磨損，隨滑動速度的增大，剪切將發生在離界面不遠處的材料內部，磨損率急劇增加；勻速滑動階段，外載荷作用趨于穩定，但仍存在微凸體間的相互作用，磨損率略有波動，后隨接觸峰點的磨損，磨損率平緩增大。

[1] 戴雄杰.摩擦學基礎[M].上海：上海科學技術出版社, 1984.

[2] Jaeger J C.Moving Sources of Heat and the Temperature at Sliding Contacts [J].Proc.Roy.Soc., NSW, 1942, 76(3): 203-224.

[3] Bhushan B.Temperature and Friction of Sliding Surfaces [D].MIT, Cambridge, Massachusetts.1971.

[4] Bhushan B.Magnetic Head-Media Interface Temperatures: Part 1-Analysis [J].ASME Journal of Tribology, 1987, 109(2):243-251.

[5] Johansson L, Klarbring A.Thermo-elastic Frictional Contact Problems-Modeling, Finite-Element Approximation and Numerical Realization [J].Computer Methods in Applied Mechanics and Engineering, 1993, 105(2): 181-210.

[6] Gao Jianqun, Lee Si C, Ai Xiaolan, et al.An FFT-based Transient Flash Temperature Model for General Three-dimensional Rough Surface Contacts [J].ASME Journal of Tribology, 2000, 122(3): 519-523.

[7] Liu Shuangbiao, Wang Qian.A Three-dimensional Thermo-mechanical Model of Contact between Non-conforming Rough Surfaces [J].ASME Journal of Tribology, 2001, 123(1):17-26.

[8] Liu Geng, Wang Qian, Liu Shuangbiao.A Three-dimensional Thermo-elastic Asperity Contact Model for Two Nominally Flat Surfaces in Contact [J].ASME Journal of Tribology, 2001.123(3):595-602.

[9] Liu Geng, Wang Qian, Ao Y.Convenient Formulas for Modeling Three Dimensional Thermo-mechanical Asperity Contacts[J].Tribology International, 2002, 35(7):411-424..

[10] Cho S-S, Komvopoulos K.Thermo-elastic Finite Element Analysis of Subsurface Cracking Due to Sliding Surface Traction [J].ASME J.Eng.Mater.Technol., 1997, 119(1):71-85.

[11] Gong Z-Q, Komvopoulos K.Mechanical and Thermo-mechanical Elastic-plastic Contact Analysis of Layered Media with Patterned Surfaces [J].ASME Journal of Tribology, 2004, 126(1):9-17.

[12] Gong Z-Q, Komvopoulos K.Thermo-mechanical Analysis of Semi-infinite Solid in Sliding Contact with a Fractal Surface [J].ASME Journal of Tribology, 2005, 127(2):331-342.

[13] 黃鍵萌, 高誠輝, 李友遐.粗糙表面基于G-W接觸的三維瞬態熱結構耦合[J].機械強度,2008, 30(4):72-75.

[14] 黃鍵萌, 高誠輝.彈塑性粗糙體/剛體平面滑動摩擦過程熱力耦合分析[J].機械工程學報, 2011, 47(11): 87-92.

[15] 賴聯鋒, 高誠輝, 黃鍵萌.雙粗糙面滑動摩擦過程應力與應變分析[J].農業機械學報, 2012, 43(12):278-282.

[16] Mulvihill D M, Kartal M E, Nowell D, et al.An Elastic-plastic Asperity Interaction Model for Sliding Friction [J].Tribology International, 2011, 44(12): 1679-1694.

[17] Zhao Qite, Wu Guoqing, Sha Wei.Deformation of Titanium Alloy Ti-6Al-4V under Dynamic Compression [J].Computational Materials Science, 2010, 50(2):516-526.

[18] 李建明.磨損金屬學[M].北京:冶金工業出版社, 1990.