談彈塑性分析在ANSYS WORKBENCH中的數值模擬

卞宏偉 高 潮

(大連海洋大學海洋與土木工程學院，遼寧 大連 116023)

談彈塑性分析在ANSYS WORKBENCH中的數值模擬

卞宏偉 高 潮

(大連海洋大學海洋與土木工程學院，遼寧 大連 116023)

總結了彈塑性力學分析邊值問題，運用ANSYS WORKBENCH有限元分析計算軟件，采用有限元方法對結構在外荷載作用下進行三維結構的靜力分析，得出了結構的應力、位移等變化形式，體現了彈塑性分析在工程數值模擬中的應用與價值。

彈塑性分析，ANSYS WORKBENCH，結構

0 引言

一般情況下，彈塑性問題會涉及到復雜的非線性本構方程而難以得到解析解答。但在一些問題中，材料在一些簡單的應力狀態且其主應力大小次序明確，如果再假定材料是理想的彈塑性或線性硬化的，則它們就成為可簡單求解的問題，例如一些梁的橫向彎曲、厚壁圓筒承受壓力、柱體扭轉等問題。在這些問題的求解中，首先從彈性區與塑性區的分解，最后來研究結構全斷面進入塑性的極限狀態，從而得到塑性極限荷載。彈塑性問題與彈性問題的根本區別在于本構方程的不同。塑性階段的本構方程有增量和全量兩種形式，相應的，彈塑性力學邊值問題的提法也有兩種不同的形式[3]。

1 彈塑性力學邊值問題

1.1 全量分析

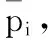
1.2 增量分析

當物體進入塑性階段且加載條件復雜時，如果只在邊界上給定荷載和位移的最后數值，不能確定物體內的應力場。只有在給定從自然狀態開始的全部邊界條件變化過程的情況下，才可能跟蹤給定的加載歷史，確定物體內應力和位移的變化過程。此時，彈塑性力學問題應該按增量或速率的形式提出。

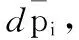
1.3 方程求解

解的唯一性。在線性彈性力學問題中，解的唯一性定理是成立的。而在彈塑性力學問題中，本構方程為非線性，且應力與應變不存在單值對應關系，因而問題就比較復雜。如果結構是簡單加載并全量理論求解，則解是唯一的。在必須采用增量理論求解的問題中，對于硬化材料，當dσij值，不能唯一的確定dεij，即dεij的解可以不唯一[4]。

彈塑性力學問題的基本求解方法仍然是位移法和應力法。由于涉及到復雜的非線性本構方程，通常情況下解析解是無法得到的，只能采用數值方法求近似解。如果材料是理想彈塑性的或線性硬化彈塑性的，則對于某些簡單彈塑性問題，可以得到解析解。

2 ANSYS WORKBENCH結構非線性靜力分析

2.1 使用線性求解非線性問題

工程中的很多問題都會涉及到諸如結構大變形、大應變、接觸狀態改變等非線性問題，早在16世紀，胡克發現了簡單的力F和位移u之間的線性關系，稱之為胡克定律：

F=Ku

(1)

非線性分析中，無法使用一組線性方程預測非線性響應，因此使用具有修正的線性近似迭代算法分析非線性問題。

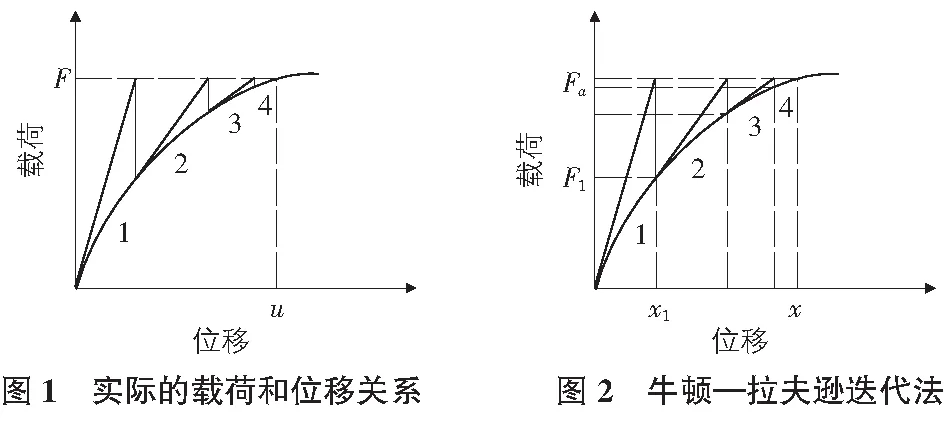
ANSYS采用牛頓—拉夫遜迭代法，每個迭代稱為平衡迭代，圖1，圖2顯示了一個完整的牛頓—拉夫遜迭代法處理一個載荷增量過程，經過4次迭代達到收斂。實際的載荷和位移關系為圖1，事先并不知道，采用線性近似迭代如圖2所示，第一次迭代中，施加總載荷Fa，對應的結果為x1，根據位移x1，計算力F1，如果F1與Fa不相等，則系統不平衡，因此根據當前的條件修正剛度矩陣，即斜率，Fa-F1的偏差，即外力與內力的偏差稱為殘差力，殘差力需要足夠小以獲得收斂解，該過程不斷重復，求得Fa=Fi。

2.2 超彈材料厚壁圓筒受內壓

本例對超彈材料厚圓柱體受內壓進行分析，參考“J.T.Oden，Finite Elements of Nonlinear Continua，McGraw-Hill Book Co.,New York,NY,1972,pp.325-331”。

無限長圓筒具有Mooney-Rivlin超彈材料，內部施加壓力P，需確定內半徑處的徑向位移和半徑為R=8.16in處的徑向應力，常數C10=80 psi；C01=20 psi，不可壓縮參數D1=0；內半徑r1=7 in；外徑r2=18.625 in；壓力P=90 psi～150 psi。

由超彈材料的屬性看圖3的三條應力—應變曲線，最上面的是雙軸應力狀態下的應力—應變曲線；中間的為剪切應力狀態下的應力—應變曲線；最下邊的為單軸應力狀態下的應力—應變曲線。數值模擬及結果分析。內孔徑向變形過程見圖4，正應力變化過程見圖5。應力應變分析結果見表1。

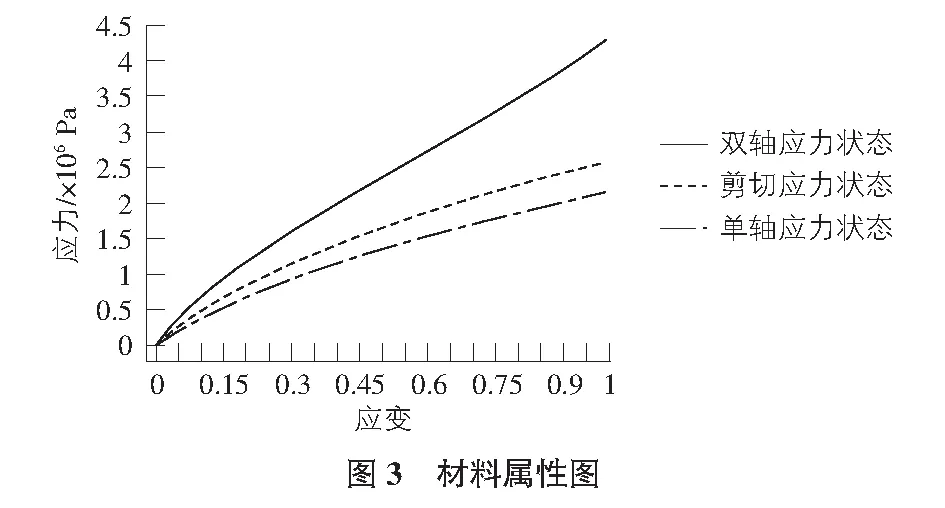
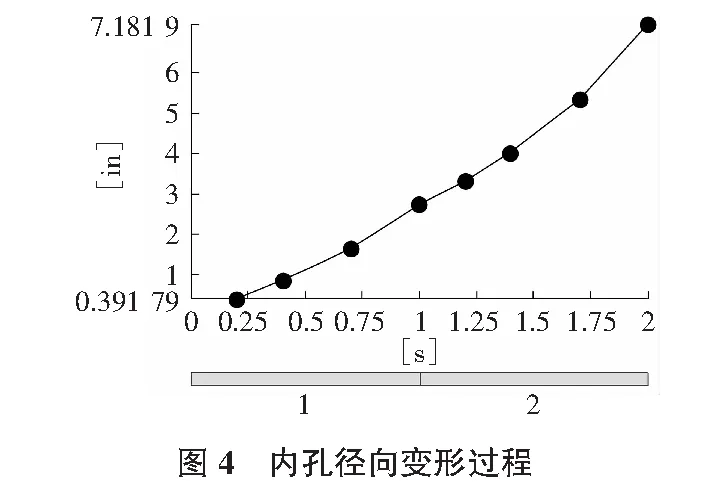
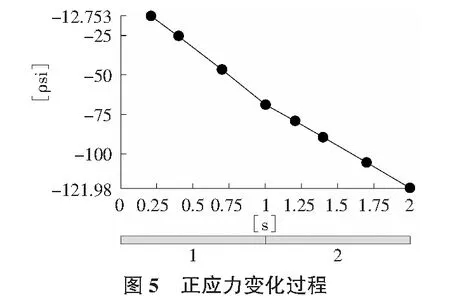
表1 應力應變分析結果

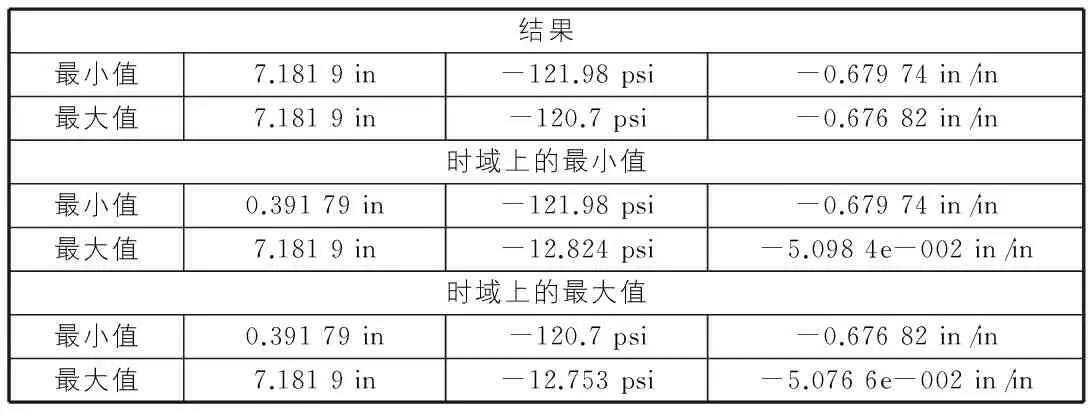
結果最小值7.1819in-121.98psi-0.67974in/in最大值7.1819in-120.7psi-0.67682in/in時域上的最小值最小值0.39179in-121.98psi-0.67974in/in最大值7.1819in-12.824psi-5.0984e-002in/in時域上的最大值最小值0.39179in-120.7psi-0.67682in/in最大值7.1819in-12.753psi-5.0766e-002in/in

ANSYS WORKBENCH數值模擬與理論解對比如表2所示。

表2 數值模擬與理論解對比

3 結語

文中首先介紹了彈塑性分析力學邊值問題的提法的不用形式，并通過ANSYS WORKBENCH對超彈材料厚壁圓筒受內壓模型進行的三維有限元結構非線性靜力分析，分別得出內徑處徑向變形和半徑為8.16處的徑向正應力分布特征，提取重要數據，并與應用理論方法得出的理論解進行對比。結果表明，在一般情況下，彈塑性問題涉及到復雜的非線性本構方程而難以得到的解析解答，可以在誤差允許的范圍內通過ANSYS WORKBENCH進行靜力分析，并能對結構的變形的受力情況作出合理的評價，而且在理論方法不能方便快捷的得出解析解時，能簡單、快速、方便、直觀的得出結論，相對于ANSYS的模型導入和環境集成更加便捷。

[1] 蔣友諒.非線性有限元法[M].北京：科學出版社，1988.

[2] Wilkinson S.Simplified procedure for seismic analysis of asymmetric Buildings[J].Computers and Structures,2001,79(32):36.

[3] 徐秉業，劉信聲.結構塑性極限分析[M].北京：中國建筑工業出版社，1985.

[4] 楊桂通.彈塑性力學[M].北京：人民教育出版社，1998.

[5] J.T.Oden.Finite Elements of Nonlinear Continua[M].McGraw-Hill Book Co.,New York,NY,1972：325-331.

Introduction to numerical simulation of elastic plastic analysis on ANSYS WORKBENCH

BIAN Hong-wei GAO Chao

(Ocean and Civil Engineering Institute, Dalian Ocean University, Dalian 116023, China)

Summarizes elastic plastic mechanics analysis the boundary value problems, using the finite element analysis software ANSYS WORKBENCH, using the finite element method on structure in the external load, make 3D structure static analysis, get stress displacement and other changes of structure. To reflect elastic plastic analysis application and value in engineering numerical simulation.

elastic plastic analysis， ANSYS WORKBENCH， structure

1009-6825(2014)18-0032-03

2014-04-12

卞宏偉(1990- )，男，在讀碩士； 高 潮(1958- )，女，教授

TU313

A