基于模型開發方法的電動汽車永磁同步電機矢量控制算法研究與應用*

黃智宇， 鮮知良， 李景俊， 尤云功

(1. 重慶郵電大學 自動化學院，重慶 400065； 2. 重慶高校汽車電子與嵌入式 系統工程研究中心，重慶 400065)

0 引 言

當今世界，環境和能源問題越來越受到國際社會的重視，電動汽車以其清潔、高效和安全成為世界各國的研究熱點。電動汽車的主要技術分為： 底盤和車身技術、能源技術以及驅動技術，其中以驅動技術尤為復雜[1]。電動汽車要求驅動電機具有能夠頻繁起動/停車、加速/減速，過載能力強，調速范圍大，既要能運行在恒轉矩區，又要能運行在恒功率區。永磁同步電機(Permanent Magnet Synchronous Motor, PMSM)因其具有功率密度高、效率高等一系列優點，多被各整車廠商選作驅動電機[2，3]。

永磁同步電機控制技術主要分為矢量控制(Field Orientation Control, FOC)技術和直接轉矩控制(Direct Torque Control, DTC)技術[4-6]。DTC雖然具有瞬態響應良好、受電機參數變化影響小等優點，但其起動和低速性能差，電流和轉矩有很大的脈動。FOC具有良好的中、低速性能，雖然其轉速及扭矩的瞬態響應較慢，但其目標轉速和扭矩的響應時間可以通過算法改進，在文獻[7-11]中有詳細研究。本文采用FOC作為永磁同步電機的控制算法。

隨著汽車電子軟件的日益增多，其開發過程也變得更復雜，很難形成統一的開發流程，對驅動電機控制軟件的開發亦是如此，這導致電機控制軟件的開發周期長、開發效率低。為了提高電機控制軟件的開發效率，把對電機軟件的開發集中在控制算法上。本文采用基于模型的開發方法[12]，結合模型的實時開發環境，實現FOC算法設計、模型搭建、代碼生成和硬件調試的快速一體式開發。

1 PMSM數學模型及FOC算法

1.1 PMSM的數學模型

由于PMSM是一個多變量、強耦合的復雜系統，為了更好地分析和簡化研究，在討論PMSM的多變量數學模型時，常作以下假設[13]：

(1) 忽略空間諧波和漏磁通的影響；

(2) 忽略磁路飽和，各繞組的自感和互感都是線性的；

(3) 忽略鐵心損耗和飽和，默認永磁材料電導率為零；

(4) 不考慮頻率和溫度變化對繞組電阻的影響，定子各相繞組參數一致；

(5) 永磁體轉子磁鏈幅值恒定，氣隙在空間磁場呈正弦分布。

在dq坐標系下，PMSM的數學模型為[14]

(1)

式中：ud、uq——定子的d、q軸電壓；

id、iq——定子的d、q軸電流；

Ld、Lq——d、q軸電感；

Rs——定子電阻；

ω——轉子角速度；

ψf——磁鏈；

np——磁極對數；

TL——負載扭矩；

B——粘滯系數；

J——轉動慣量。

永磁同步電機的電磁轉矩方程為

Te=3np[Ψfiq+(Ld-Lq)idiq]/2

(2)

本文試驗中的電動汽車驅動電機為表面式永磁同步電機，其d軸和q軸電感相等，故得到簡化的電磁轉矩方程為

Te=3npΨfiq/2

(3)

由式(3)可知，通過控制iq電流即可控制永磁同步電機的電磁轉矩，能夠實現如同直流電機的控制，具有很好的解耦特性。

1.2 FOC算法

通過坐標變換，FOC算法將PMSM的定子電流分解到轉子同步旋轉坐標系中，把定子電流分為勵磁電流分量id(直軸電流分量)和轉矩電流分量iq(交軸電流分量)，對兩個分量分別加以控制，從而獲得很好的解耦特性。PMSM的FOC框圖如圖1所示。

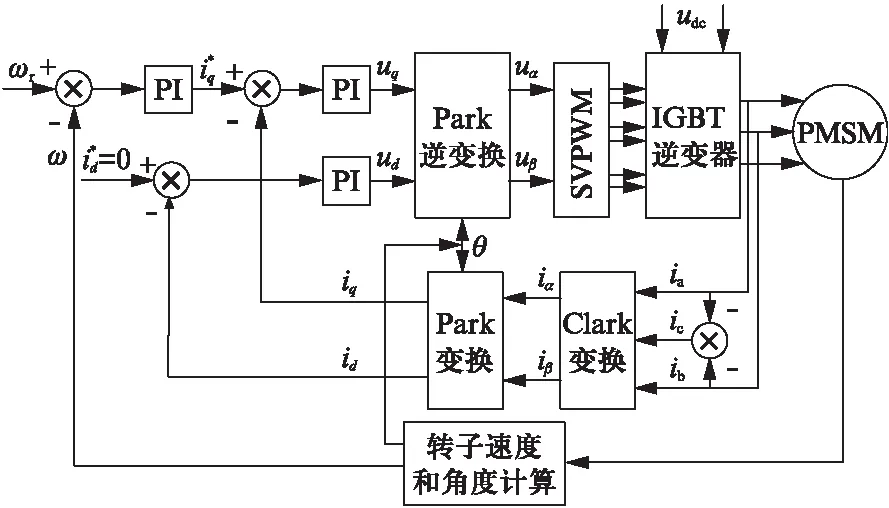
圖1 PMSM的FOC框圖

2 基于模型的FOC設計

基于模型的設計，是以實時軟件為開發平臺，實現快速的算法建模、微控制器驅動集成、代碼自動生成、軟件/處理器/硬件在環測試等[15]。

本文以MATLAB與CCS IDE為軟件平臺，具體的實現過程分： FOC算法設計、FOC子系統代碼生成與測試、集成微控制器及外設驅動、集成任務調度、整個模型自動代碼生成與優化。

2.1 FOC算法設計

FOC算法難點是SVPWM模塊設計，其以三相對稱電動機定子理想磁鏈圓為參考標準，對三相逆變器不同開關模式作適當的切換，從而形成PWM波形，以所形成的磁鏈矢量來追蹤其準確磁鏈圓。三相逆變器由三組半橋，6個開關組成。依次定義逆變器的8種工作狀態：v0=[000]，v1=[001]，v2=[010]，v3=[011]，v4=[100]，v5=[101]，v6=[110]，v7=[111]，作為基本電壓矢量，把空間均分為6個扇區，來合成空間電壓矢量。逆變器開關狀態為[001]如圖2所示。空間電壓矢量分布如圖3所示。

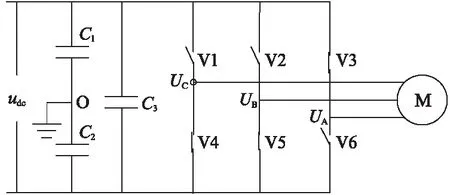
圖2 逆變器開關狀態為[001]

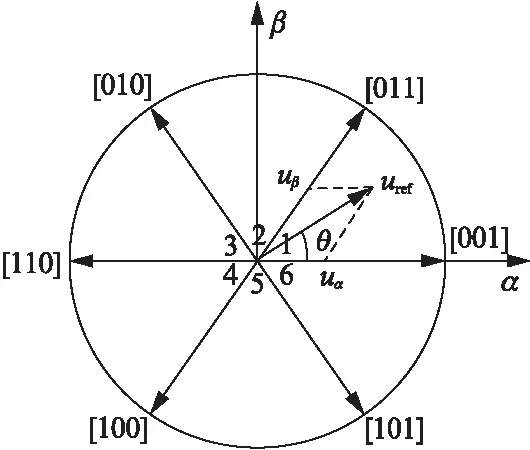
圖3 空間電壓矢量分布

為了減少逆變器開關切換次數，達到減小開關損耗的目的，本文設計7段式SVPWM，將基本電壓矢量作用時間順序選定為： 在每次開關狀態轉換時，只改變其中一個逆變橋的開關狀態，以 Ⅰ 扇區(0°≤θ≤60°)為例，空間電壓矢量uref由基本電壓矢量v1，v3合成，設定v1，v3的作用時間分別為T1、T3，零矢量的作用時間分別為T0、T7，PWM周期為Ts。在一個PWM周期內，逆變器的開關切換順序為： 0-1-3-7-7-3-1-0，基本電壓矢量在一個PWM周期內開關切換順序如圖4所示。

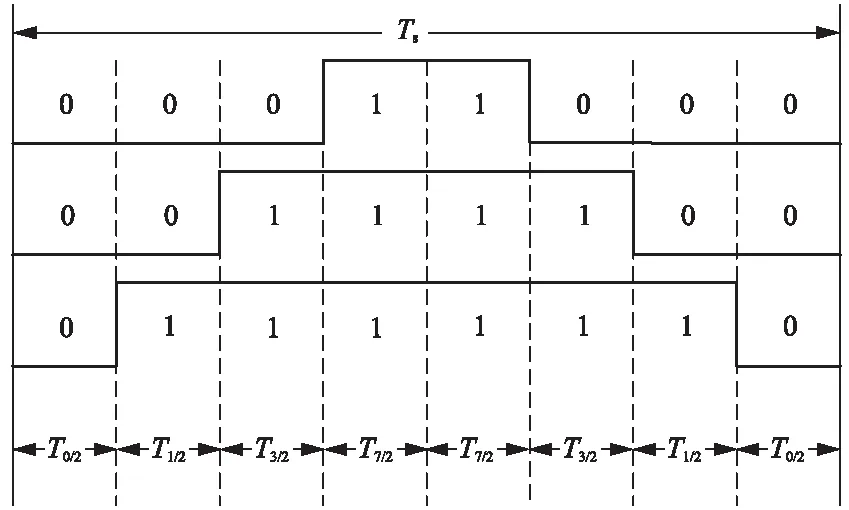
圖4 Ⅰ扇區一個周期內開關切換順序

具體的SVPWM實現方式可分為： 確定合成電壓矢量uref所處扇區和計算基本電壓矢量作用時間。

(1) 確定合成電壓矢量uref所處扇區。

由圖1可知，uα，uβ作為逆變器的輸入，來合成電壓矢量uref，假定合成電壓矢量uref落在第Ⅰ扇區，由圖3可知其等價條件： 0°< arctan(uβ/uα)<60°。同理，可以判斷出合成電壓矢量uref落在第x扇區的充要條件。空間電壓矢量所在扇區判斷如表1所示。

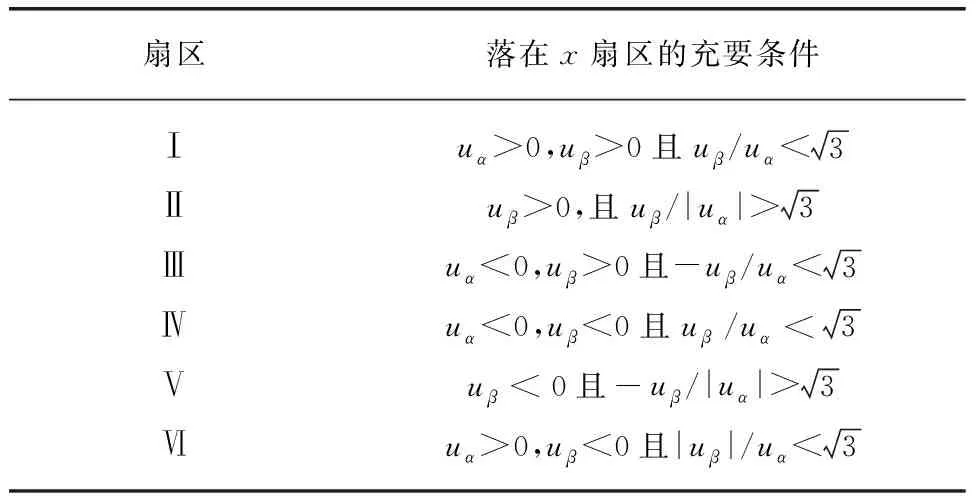
表1 空間電壓矢量所在扇區判斷

(2) 計算基本電壓矢量作用時間。

以第Ⅰ扇區空間電壓矢量uref為例，設定其相鄰基本電壓作用時間分別為T1、T3，零矢量的作用時間分別為T0、T7，PWM周期為Ts，θ為uref與v1之間的夾角，如圖3所示。由伏秒平衡法得

(4)

解得

(5)

(6)

(7)

同理，可求得uref在其他扇區中各基本電壓矢量的作用時間。應注意在合成某空間電壓矢量時，相鄰基本電壓矢量作用時間的計算，以免發生過調制。相鄰基本電壓矢量作用時間的計算流程圖如圖5所示，其中，Tk、Tk+1分別為相鄰電壓矢量的作用時間，Ts為PWM周期。

圖5 相鄰基本電壓矢量作用時間的計算流程圖

2.2 FOC子系統代碼生成與測試

本文選擇TI公司的F28335作為電機控制器芯片，CPU頻率150MHz，開發環境為CCS IDE，選擇運行方式為處理器在環測試(Processor In the Loop， PIL)，并對FOC算法子系統進行C代碼生成及封裝，命名為算法子模塊，采用PIL方式對算法子模塊進行測試。

2.3 集成微控制器及外設驅動

要實現從仿真模型到C代碼生成、對控制器的實時控制，須在仿真模型中集成F28335的微控制器驅動及外設驅動，如ADC驅動、PWM驅動、RESOLVER驅動等。

(1) ADC驅動。本文主要涉及3種模擬量的采集： 通過電流傳感器測得的兩相定子電流Ia、Ib(第三相電流Ic可以通過Ia+Ib+Ic=0計算得到)，及速度請求信號。這3種模擬信號分別接至不同的ADC通道。

(2) PWM驅動。PWM信號用于驅動逆變橋，產生三相正弦電流波形。本文中FOC算法模塊的輸出數據格式設定為Q17定點型，其數值范圍為-1到1，需要使PWM周期、PWM比較值與FOC的輸出信號相匹配。其參數設置包括： 周期設置、占空比設置、使能設置、死區時間設置。

(3) RESOLVER驅動。RESOLVER旋轉變壓器用于對轉子角絕對位置檢測和轉速測量，需要設置好旋變激勵信號頻率。

2.4 異步調度任務

通過FOC算法設計，在算法模型中集成相應的微控制器驅動及外設驅動之后，需要考慮： (1) 在FOC算法之前起動ADC轉換；(2) FOC算法觸發與PWM信號保持同步；(3) PWM信號完成后再次起動ADC轉換。本文采用任務調度方式，把不同的算法模塊放置在不同的任務下，并設置好任務的執行時間。

當完成以上設計后，編譯整個模型，進行模型的仿真試驗，驗證FOC算法；然后完成PMSM控制軟件的代碼生成與優化，生成可執行文件；最后下載到電機控制器中，即可在電動汽車驅動電機及測功機系統測試平臺上進行臺架試驗。

3 仿真試驗及結果分析

在完成FOC模型設計基礎之上，通過仿真試驗來模擬電動汽車的起動和加速兩種行駛工況。仿真試驗中，電機模型的主要參數：p=3，Rs=2.875Ω，L=0.835mH，J=0.0008kg·m2，B=0.002，Ψf=0.85Wb。電機在兩種工況下的轉速及定子三相電流波形如圖6所示。

由圖6(a)、圖6(b)可以看出，在給定轉速為3000r/min時，電機在起動過程中存在較小的超調量。經過一定時間的調整后達到給定轉速，轉速響應平穩，同時電機在起動瞬間，需要一個較大的三相電流，當電機達到給定的目標轉速后，三相電流平穩。由圖6(c)、圖6(d)可以看出，電機在0.02s時開始從1000r/min加速，在較小的時間內達到1500r/min，電機在起動和加速時，都需要一個較大的三相電流。因此，三相電流在加速過程中有較大脈動，電機運行在較高轉速時，三相電流頻率也相應增大。

由仿真結果可看出，該設計算法能滿足永磁同步電機中、低速的調速要求，轉速響應快速。

4 臺架試驗及結果分析

完成上述仿真試驗后，在電動汽車驅動電機及測功機系統平臺進行臺架試驗。采用Remy公司的HVH250-090S永磁同步電機來模擬純電動汽車的驅動電機。電機的主要參數： 額定功率60kW，額定電壓320V，額定輸出扭矩210N·m，磁極10對。采用RMS公司的PM100電機控制器作為主控制器；直流電壓通過整流柜輸出。

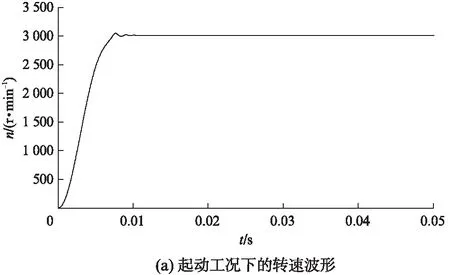
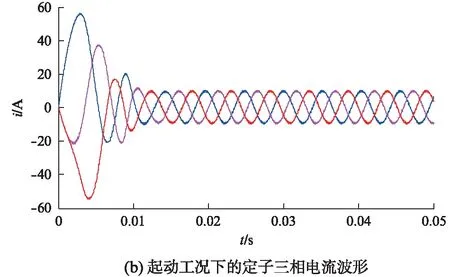
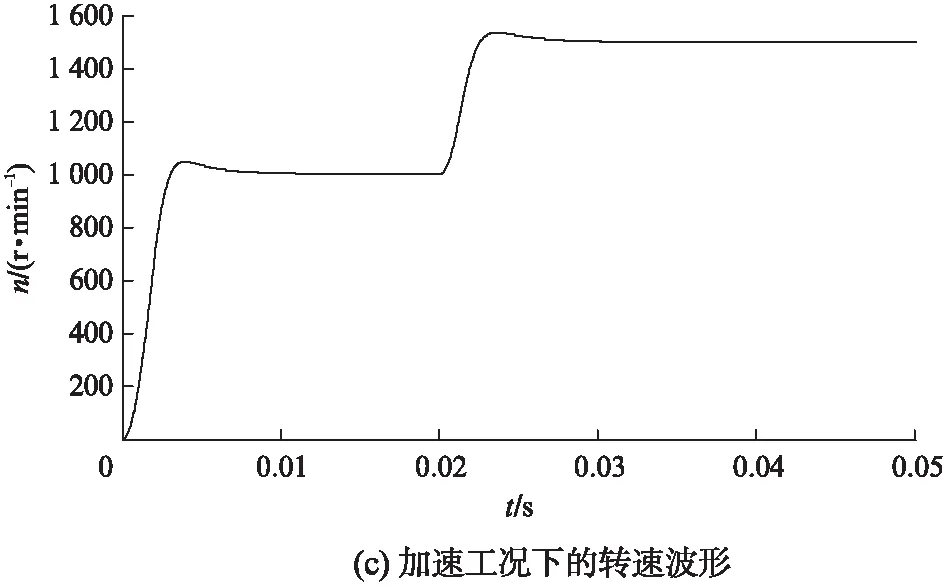
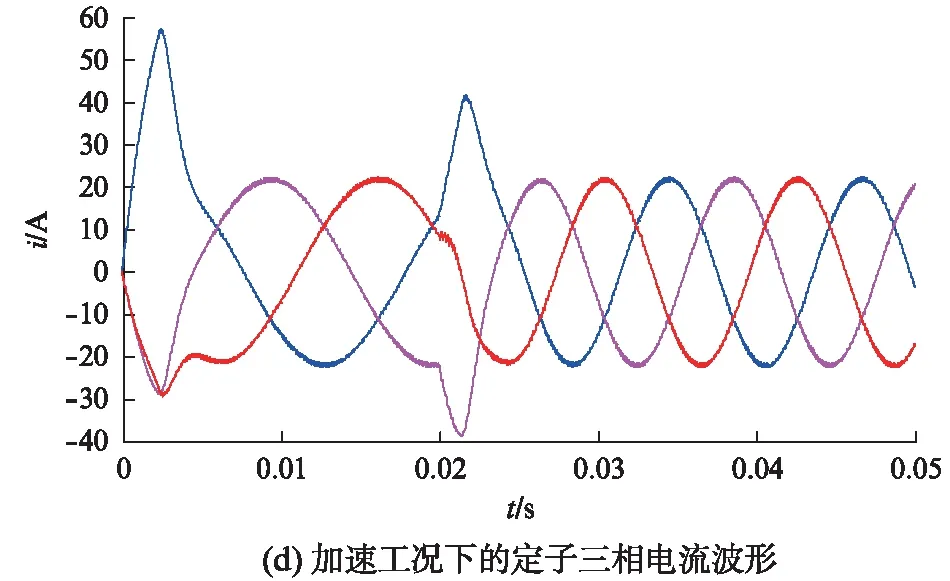
圖6 電機在兩種工況下的轉速及定子三相電流波形

在強電試驗之前，需要對電機控制器的PI參數進行設定，使電機輸出穩定的轉速。其PI參數設置為：① 速度環：Kp=16，Ki=0.0008；② 電流環：Kp=0.01，Ki=0.0004。

基于臺架，電機在起動、加速工況下的轉速及三相電流波形，如圖7所示。

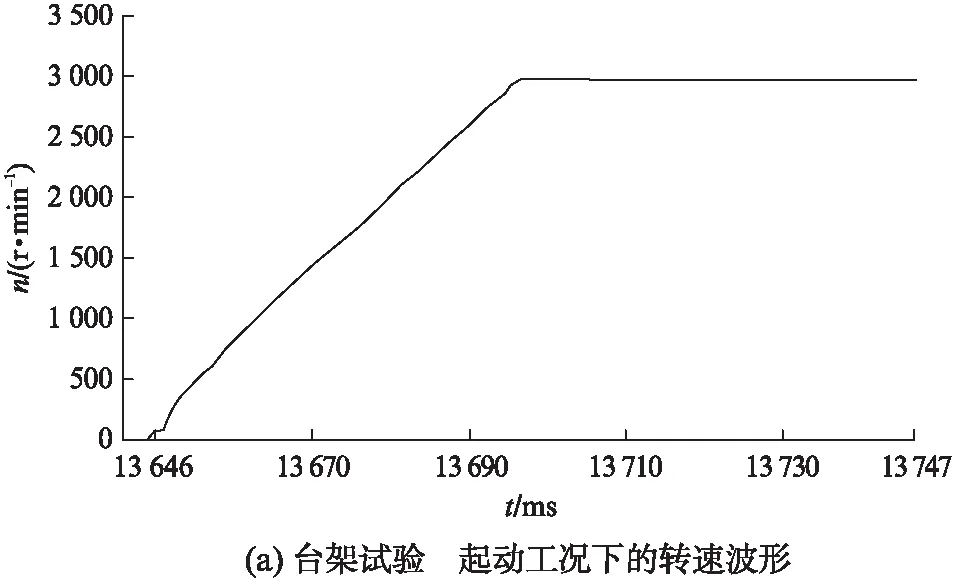
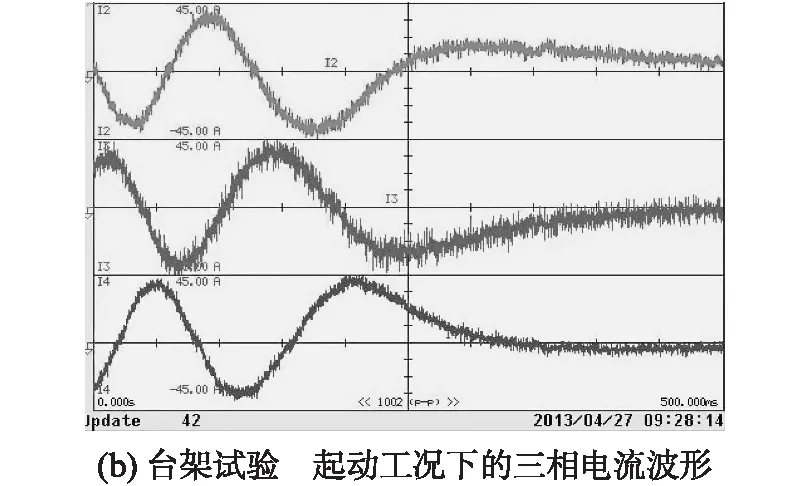
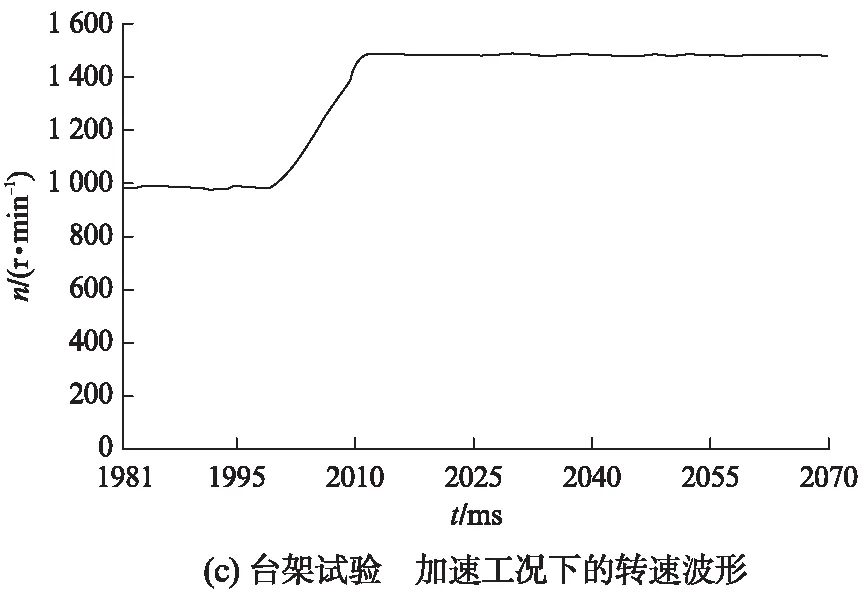
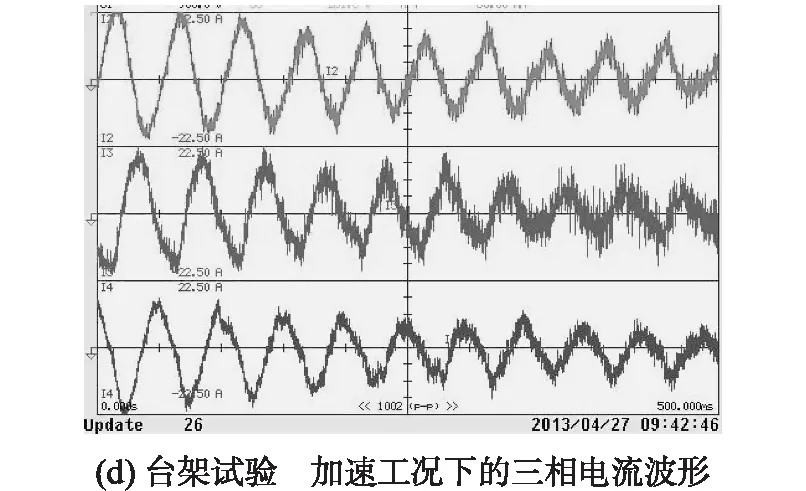
圖7 基于臺架試驗的兩種工況下的轉速及電流波形

由圖7(a)、圖7(b)中可以看出，在給定轉速為3000r/min時，電機在起動過程中存在較小的超調量，轉速響應平穩；在電機起動瞬間，三相電流存在較大的脈動。由圖7(c)、圖7(d)中可以看出，電機在2s時開始從1000r/min加速，在1s的時間內達到1500r/min，電機達到目標轉速后，三相電流頻率也相應增大。

臺架試驗表明，通過起動和加速工況試驗來模擬電動汽車行駛工況，電機轉速響應快速，滿足基本的電機起動、加速要求。

5 結 語

本文從算法設計到實現對電機的控制，開發流程簡單，不需要專注于微控制器底層硬件驅動開發，大大縮短電機控制器控制軟件的開發周期，將更多的精力用于電機控制算法的設計，提升電機調速性能，并應用于電動汽車的行駛工況中。另外，開發平臺建立快速、成本較低，具有很好的實用價值。本文采用基于模型的電機控制算法開發流程，仿真試驗驗證了FOC算法的可行性，并將優化后的代碼應用于對電動汽車驅動電機控制系統中，在電機及測功機系統測試平臺上模擬電動汽車兩種行駛工況，實現了對電機轉速控制的驗證試驗。試驗結果表明，本文所設計的FOC算法具有良好的中、低速性能。

【參考文獻】

[1] CHAN C C. The state of the art of electric, hybrid, and fuel cell vehicles [J]. Proceedings of the IEEE, 2007,95(4)： 704-718.

[2] PREINDL M, BOLOGNANI S. Model predictive direct speed control with finite control set of PMSM drive systems [J]. 2013，28(2)： 1007-1015.

[3] 金寧治,王旭東,李文娟.電動汽車PMSM MTPA控制系統滑模速度控制[J].電機與控制學報,2011,15(8)： 52-58.

[4] BLASCHKE F. A new method for the structural decoupling of AC induction machines [C]∥Conf Rec IFAC 1971： 1-15.

[5] SWIERCZYNSKI D, WOJCIK P, KAZMIERK-OWSKI M P, et al. Direct torque controlled PWM inverter fed PMSM drive for public transport [C]∥Advanced Motion Control, 2008 AMC’08 10th IEEE International Workshop on IEEE, 2008： 716-720.

[6] 張華強,王新生,魏鵬飛,等.基于空間矢量調制的直接轉矩控制算法研究[J].電機與控制學報,2012,16(6)： 13-18.

[7] LAI C K, SHYU K K. A novel motor drive design for incremental motion system via sliding-mode control method [J]. Industrial Electronics, IEEE Transa-ctions on, 2005,52(2)： 499-507.

[8] ELBULUK M, LI C. Sliding mode observer for wide-speed sensorless control of PMSM drives [C]∥Industry Applications Conference, 2003 38th IAS Annual Meeting Conference Record of the IEEE, 2003,1： 480- 485.

[9] 宋傳玉.永磁同步電機的模糊神經網絡控制方法[J].電機與控制應用,2008,35(6)： 27-29.

[10] 童克文,張興,張昱,等.基于新型趨近律的永磁同步電動機滑模變結構控制[J].中國電機工程學報,2008,28(21)： 102-106．

[11] 方斯琛,周波,黃佳佳,等.滑模控制永磁同步電動機調速系統[J].電工技術學報,2008,23(8)： 29-35.

[12] 劉杰.基于模型的設計及其嵌入式實現[M].北京： 北京航空航天大學出版社,2010.

[13] CAPONIO A, CASCELLA G L, NERI F, et al. A fast adaptive memetic algorithm for online and offline control design of PMSM drives [J]. Systems, Man, and Cybernetics, Part B： Cybernetics, IEEE Transactions on, 2007,37(1)： 28- 41.

[14] LI S, ZHOU M, YU X. Design and implementation of terminal sliding mode control method for PMSM speed regulation system [J]. Industrial Informatics, IEEE Transactions on， 2013，9(4)： 1879-1891.

[15] 劉杰，周宇博.基于模型的設計——MSP430F28027F28335DSP篇[M].北京： 國防工業出版社,2011.