基于圖論的DNA微陣列數據聚類算法

宋 佳，許 力，孫 洪

(1. 浙江大學電氣工程學院，杭州 31002 7；2. 蘇州市職業大學電子信息工程系，江蘇 蘇州 21 5104)

基于圖論的DNA微陣列數據聚類算法

宋 佳1,2，許 力1，孫 洪2

(1. 浙江大學電氣工程學院，杭州 31002 7；2. 蘇州市職業大學電子信息工程系，江蘇 蘇州 21 5104)

傳統的聚類算法用于DNA微陣列數據分析時，多數只能生成一種聚類結果，無法識別出與多組不同基因表達模式相類似的基因。針對該問題，提出一種基于圖論的聚類算法，采用一個有向無權圖來描述需要分析的DNA微陣列數據，分別計算該圖具有最小割權值和第二小割權值的圖割。測試結果表明，該算法可以有效地探測聚類結果空間并輸出一組可能性較高的聚類結果，與Fuzzy-Max、Fuzzy-Alpha、Fuzzy-Clust等聚類算法相比具有更高的準確性。

微陣列；基因表達數據；聚類分析；圖割；圖論；最小割

1 概述

DNA微陣列技術的發展使得研究人員可以同時監測并獲得各種環境下成千上萬個基因的表達水平，產生了海量的基因表達譜數據[1]，從而深入地認識諸多生物過程的本質，如基因功能、發育、癌癥、衰老和藥理等。因此，建立能夠準確處理和分析DNA微陣列數據集的方法是目前生物信息學發展的一個重要方向。聚類算法就是用于查找功能相關的基因和疾病新子群的主要方法之一。聚類算法根據目標研究對象的屬性數值，采用數學方法對其進行分類和整理，將具有相似屬性的事物聚為一類，使得同一類的事物盡可能相似，而不同類的事物間有較大的差別。因此，聚類算法的準確性對于準確識別功能相關的基因起著關鍵性的作用，是進行表達數據中數據挖掘的第一步，其效果直接影響后續的表達譜數據分析性能。

聚類算法可以分為有監督的聚類算法(或分類，classification)、無監督的聚類算法和混合聚類算法。在有監督的聚類中，聚類基于一個給定的參考方向集或類別集；在無監督聚類中，聚類分析預先不知道類別信息，沒有訓練集；混合聚類通常先進行無監督聚類，確定一些類，再用神經網絡或支持向量機這些可以學習數據類別之間決策邊界的分類器，將新基因歸到不同的類內。基因表達陣列實驗尚處于早期階段，無監督聚類算法仍是最常用的。

目前，已有大量的無監督聚類算法和軟件被開發出來并用于分析DNA微陣列的數據，如K-means算法、平均連鎖聚類、基于最小遍歷樹聚類法、自組織映射等。這些聚類算法將相應條件下表達相似的基因歸為一類。在實際應用中，由于噪聲等原因，存在大量的基因不屬于任何一個聚類，同時也存在一些基因可以在不同生物過程中與不同的基因分組一起發揮不同的作用，從而出現在多個聚類中。而上述的這些聚類算法大多只能生成一種聚類結果，無法識別出與多組不同的基因表達模式相類似的基因，難以獲得在不同條件下與多組基因共調控的基因之間的關系。近年來，針對這一缺陷，研究者們提出了一些更為復雜也更加適宜于基因表達數據分析的的聚類算法[2-3]，這些算法大多基于模糊聚類(fuzzy clustering)。模糊聚類算法[4-5]的特點是并沒有強制將每個基因歸入到某個特定的聚類中，而是分別計算每個基因歸屬各個聚類的隸屬度，通過隸屬度值的大小來表示基因隸屬某個聚類的程度高低。但是，這些模糊聚類算法也存在若干缺陷，如模糊參數值很難設置、計算復雜度高，算法也常常無法識別出所有的聚類。

圖論(graph theory)是離散數學的一個分支，它以圖為研究對象，研究頂點(vertex)和邊(edge)組成圖形的數學理論和方法。圖論中的圖形通常可以用來描述某些事物之間的某種特定關系，例如用頂點代表事物，用連接兩頂點的邊表示2個事物間具有某種關系。因為圖論是一門研究較早并且已經發展成熟的學科，具有較好的數學基礎，應用圖論方法解決生物信息學問題也越來越引起學者的重視。基于圖論的聚類算法主要包括Random Walk、CHAMELEON、AUTOCLUST等[6-7]。近年也有一些利用圖的著色理論[8]、閾值剪枝[9]，以及譜圖[10]等理論的聚類算法被提出。這些算法也只能生成一種聚類結果。

本文提出一種以圖論為基礎的聚類算法，將DNA微陣列數據集映射成加權圖，分別計算圖的最小割和第二最小割，并依據每個圖割，將圖分別分割成2個子圖，在每個子圖上迭代地應用這個算法，直到沒有新的集群出現為止。此外，本文還設計了一種可以在多項式時間內計算出有權圖的第二最小割的算法，并從理論上證明其正確性，以持續更新并輸出一組可能性較高的聚類結果。

2 模型與算法

2.1 D NA微陣列數據的獲取和預處理

DNA微陣列也稱為基因微陣列，目前有2種模式：cDNA微陣列和Affymetrix基因芯片(或寡核苷酸陣列)，它們的原理相同，即利用4種核苷酸(A, T, C, G)之間兩兩配對互補的特性，使2條在序列上互補的單核苷酸鏈形成雙鏈(即雜交，hybridization)。以cDNA微陣列為例，在一個表面處理過的固體支撐物(通常是尼龍或玻璃)上，cDNA以固定的模式排列。用于測試的mRNA樣本被反轉錄成cDNA并用熒光染色標記，這些cDNA與陣列上的DNA探針進行雜交，用激光顯微鏡或熒光顯微鏡檢測雜交后的芯片，獲取熒光強度，最后通過圖像處理和分析得到測試樣本中mRNA的豐度信息。

計算機讀出的微陣列數據矩陣C(N×M)表示N個基因在M個樣本(或M個不同的實驗條件)上的表達矩陣：

矩陣C中每一行代表一個基因，每一列代表一張芯片上基因的數據。cij為基因i在實驗j中的表達值。依據基因芯片的實驗原理，cij取為相對的熒光強度比值：

其中，IR為芯片上紅色熒光劑(樣本組基因)的強度；IG為芯片上綠色熒光劑(對照組基因)的強度，對其分別取對數可以避免以下差異：當基因高表達時，表達比在(1,+∞)，當基因低表達時，表達比在(0,1)，兩者存在不對稱性。基因可以看作是含有M維實數的向量，而樣本可以看作是N維實數的向量。根據不同的實驗，基因表達值可以采用同樣的算法分別對實驗條件(列)或基因表達譜(行)進行聚類。

在進行聚類時，都需要對數據之間的相似度進行評估，這個評估通常采用距離函數來實現。目前有2種距離函數廣泛用于比較基因表達譜：歐幾里德距離函數和皮爾森距離函數。具體函數的選擇主要取決于研究者想要測量的特性。本文采用歐幾里德距離來度量基因之間的相似性。給定2個向量：它們之間的歐幾里德距離可以用下式來計算：

歐式距離測量空間中2個點的絕對距離，故同時考慮了矢量的方向和幅度。若直接使用原始數據進行計算，則表達譜幅度相似的基因將被認為是相似的。但生物學上更傾向于尋找表達水平不同而表達譜形狀相似的基因，因此，在使用歐式距離前需對微陣列數據作歸一化處理：

其中，μi和σi分別是ci的均值和方差。

2.2 圖的構建

在對DNA微陣列數據歸一化處理后，采用一個無向有權圖G(V, E, W)來描述需要分類的微陣列數據，圖的頂點V代表基因，兩頂點之間的歐式距離如果小于給定的閾值T，則2個頂點由邊界連接。每條邊界都有一個權值，連接頂點vi和vj的邊界權值可以表示為：

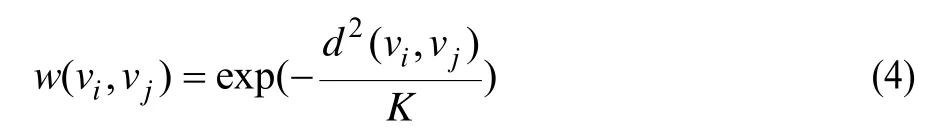
其中，d( vi, vj)即兩數據點之間的歐式距離；K為常數。很明顯距離越大，則對應的邊界權值越小。為了便于分析，本文假定圖G是連通的。因為即使圖G不連通，也可以分別在每個連通的子圖上繼續之后的工作，結果仍然適用。

2.3 圖的最小割和第二最小割計算

2.3.1 最小割計算

最小割問題[11-12]可分為s-t最小割和全局最小割。s-t最小割是指給定源點s和匯點t，能將s和t分別分割到2個子圖中的最小割。全局最小割指所有s-t最小割中值最小的割。著名的最大割最小流定理證明最大流和s-t最小割是一對對偶問題。顯然，全局最小割在計算時，需要計算(|V|(|V|-1))/2個最大流(分別對應不同的源點s和匯點t)。文獻[13]提出一種算法，只需計算(|V|-1)個最大流。給定一個有權無向圖G(V, E, W)，全局最小割的計算可通過以下步驟：(1)令min=∞，確定一個源點s；(2)枚舉匯點t，t∈V-s；(3)計算最大流，并確定當前源匯點的最小割值，若比min小，則更新min；(4)轉到步驟(2)直到枚舉完畢；(5)min即所求輸出min。

以上最小割計算中枚舉匯點的計算時間為O(|V|)。如果采用最短增廣路最大流算法來求最大流，時間復雜度是O(|V|2|E|)，則算法總復雜度為O(|V|3|E|)；而如果采用最高標號預流推進法來求最大流，時間復雜度為O(|V|2|E|0.5)，則算法總復雜度為O(|V|3|E|0.5)。文獻[14]通過優化匯點t的選擇順序，改進以往的預流推進算法，最終得到一個O(|V||E|)時間的全局最小割算法，其時間復雜度和計算一個s-t最小割是一致的。

2.3.2 第二最小割計算

最小割問題可以在多項式時間內計算出，但還不能確定割值為第二小的圖割是否也能在多項式時間內算出。下面證明它也能在多項式時間內計算出，并且可用于本文的聚類算法來探索所有的聚類結構所組成的空間。

定理1給定一個有權無向圖G(V, E, W)，具有第二小割權值的圖割可以在時間O(|E|×f(|E|,|V|))內算出，其中，f(|E|,|V|)是計算圖G全局最小割的時間復雜度。

證明：通過下列步驟可以計算出具有第二小割權值的圖割。(1)計算圖G具有最小割權值的圖割，并假定割邊集為C；(2)對于邊界(a, b)∈C，收縮(a, b)可以得到一個新圖G'；(3)計算圖G'的最小割權值的圖割，并把結果放置在集合U中；(4)把邊界(a, b)從C中移除，如果集合C非空則回到步驟(2)；(5)對集合U中的全部圖割，計算出其中具有最小割權值的圖割并輸出。

下面證明此第二小割權值算法的正確性：具有第二小割權值的圖割必須至少包括一條不在具有最小割權值的割集中的割邊，因而算法中步驟(2)～步驟(4)的窮舉搜索可以找出具有第二小割權值的圖割。因為C可能包含最多|E|條邊界，這種算法所需的時間為O(|E|×f(|E|,|V|))。

上述步驟(2)中的收縮(a, b)即刪掉點a、b及邊(a, b)，替代為新頂點n，如圖1所示。其中，對圖G中除a、b外的任意頂點v，其與n的邊權值為：

w( v, n)=w( v, a)+w( v, b) (5)

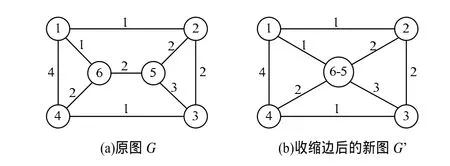
圖1 邊的收縮

2.4 高連通圖的判定

文獻[15]提出高連通圖的概念，并將其應用于無向無權圖的分割。這里對其定義進行引申后，引入之前建立的無向有權圖中，并將其作為圖分割的終止判據。

當分割所得的子圖為高連通圖時，認為它可以作為一個聚類，不再繼續分割。如圖2所示，對圖G進行分割，其中，圖2(a)為第一次分割結果，得到2個子圖G1，G2，因為G1為高連通子圖，所以不再繼續分割，圖2(b)中繼續對G2分割，得到2個高連通子圖G3，G4，分割結束。圖中的虛線表示最小割。

圖2 圖G的分割

定理2高連通圖中的任意一個頂點至少與圖G中一半以上的頂點相鄰。

證明：對于高連通圖G，如果將與其度為最小值的頂點相連的邊都去掉，則圖成為不連通圖。即這些邊可以構成一個割集，但未必是最小割。用δ(G)來表示圖G的最小度，用C來表示最小割集，則有：

因為圖G為高連通圖，由其定義可得：

由此可見，高連通圖的定義確保了圖中的所有頂點之間都聯系緊密，并且采用高連通圖作為終止判據，可以無需預先知道聚類的數目，其時間復雜度和之前求最小割的復雜度一致。

2.5 聚類算法

采用2.4節建立的計算具有最小割權值和第二小割權值的圖割的算法，來探索聚類結果組成的空間。給定一個無向有權圖G(V, E, W)來代表數據集，分別計算出具有最小和第二最小割權值的圖割。如圖3(a)所示，一個數據集可以通過計算最小割權值分為2個集群。對圖G計算出具有最小和第二最小割權值的圖割，分別可以獲取2個子圖；然后對這2個子圖重復應用此算法，直到所得的子圖為高連通子圖為止。圖3(b)說明了該過程。

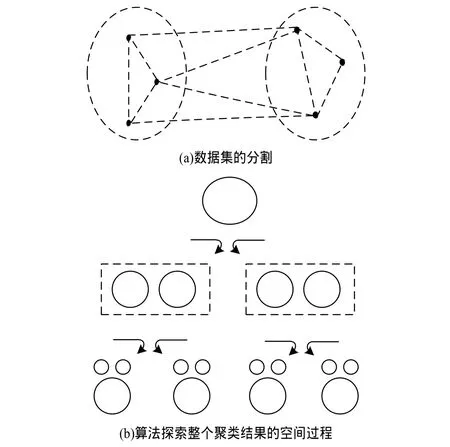
圖3 聚類算法的一個示例

3 實驗結果與分析

應用上述算法對2組基因芯片數據進行了測試。其中一組數據是從77例患者的腫瘤樣本得到的，共包含6285個基因，這些病人中有58個為擴散型大B細胞淋巴瘤(DCBCL)患者，另外19個為濾泡淋巴瘤(FL)患者。另一組數據為原發性和轉移性癌癥(PM)樣本，分別采自64個原發性癌患者和12個轉移性癌癥患者，包含了14 925個基因。在處理這2組數據集時，對式(4)中的參數做了如下取值：距離閾值T為數據點所有配對最大距離的2/3，K為最大距離平方的1/4。

與數據挖掘中通用的聚類算法相比，在對基因表達數據進行分析時更關注于算法的有效性(effectiveness)，即要求算法具有較高的準確性。因此，為了評估算法的表現，采用了一個錯誤率函數來計算聚類結果的準確性。考慮數據點的每對數據，并考慮它們是否在同一聚類中。如果在同一聚類中而聚類結果把它們放在2個不同的聚類中，或者反之亦然，則認為是一個錯誤分類。對于一個特定的聚類結果，可以計算錯誤分類的數目，并與成對的數目總和相除。這個錯誤率介于0～1之間，并可以用來衡量聚類算法的準確性。

針對本文算法的準確性，與其他一些算法做了比較，這些算法包括Fuzzy-Max，Fuzzy-Alpha，Fuzzy-Clust，Fuzzy-Single，以及Hierarchy-Single。表1和表2分別顯示了在對DLBCL和PM數據的分析上，本文算法與其他算法準確性的比較結果。對于有隨機性的算法，在對數據集做了多次測試后，計算了其中位誤差和標準偏差。

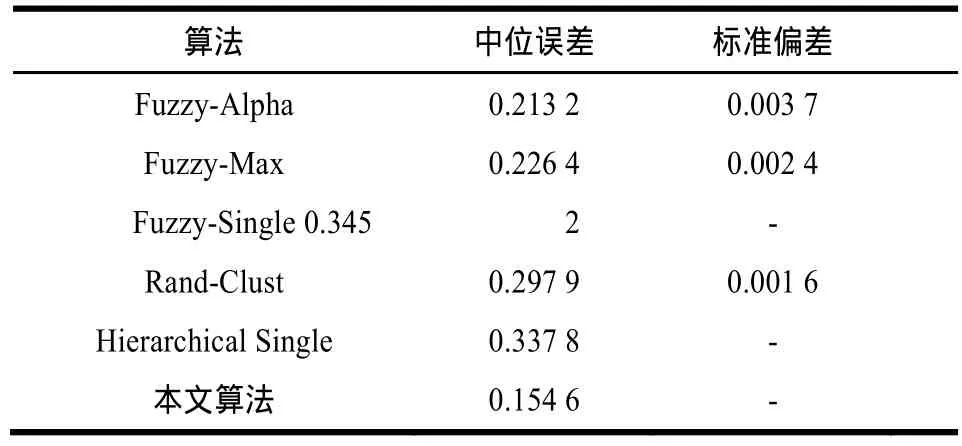
表1 本文算法與其他算法對DLBCL數據集分析的結果比較

表2 本文算法與其他算法對PM數據集分析的結果比較

從表1和表2中不難發現，在上面2組數據的聚類結果中，基于圖割的算法的準確性明顯優于其他幾種算法，而這種優勢在PM數據的聚類結果中更加明顯。

4 結束語

本文提出一種基于圖形模型和圖割算法的聚類算法，將樣本空間的整個數據集表示為一個有權圖，然后迭代地求解圖的最小割權值和第二小割權值，根據圖割將圖分割為子圖。測試結果表明，該算法可以有效地探測聚類結果空間，并具有較高的準確性。

下一步可以在之前研究的基礎上，繼續第三小割權值圖割的研究：如第三小割權值圖割的計算復雜度，以及其是否能進一步提高聚類精度等。另外，本文算法應用Hao 和Orlin提出的算法計算最小割，其時間復雜度為O(|V||E|))，聯系第二最小割的計算，則進行一次迭代就需要O(|V||E|2)時間，其計算時間復雜度仍較高。如何降低算法計算復雜度，特別是最小割計算的復雜度，也是下一步的工作方向之一。例如：當需要分類的數據點大于1 000時，可以考慮在對DNA微陣列數據建立圖形模型時，用無向無權圖模型取代之前的無向有權圖，即僅用兩頂點的連通性來表示兩基因(樣本)之間的關系。到目前為止，無向無權圖的全局最小割時間最低為O(|V||E|2/3)，因此可以進一步把算法總復雜度降低到O(|V||E|5/3)。

[1] 岳 峰, 孫 亮, 王寬全, 等. 基因表達數據的聚類分析研究進展[J]. 自動化學報, 2008, 34(2): 113-120.

[2] Bertoni A, V alentini G. Rand omized E mbedding Clust er Ensembles for Gene Expression Data Analysis[C]//Proc. of IEEE Internatio nal Conference on Science of Electronic, Technologies of Information and T elecommunications. Hammamet, Tunisia: IEEE Press, 2007: 246-252.

[3] Avogadri R, Valenini G. Fuzzy Ensemble Clustering for DNA Microarray Data An alysis[C]//Proc. of the 4th I nternational Conference on Bioinformatics and Biostatistics. Camogli, Italy: Springer, 2007: 537-543.

[4] Avogadri R, Valentini G. Fuzzy Ensemble Clustering Based on Random Pro jections for DNA M icroarray Data Analysis[J]. Artificial Intelligence in Medicine, 2009, 45(2): 173-183.

[5] Avogadri R, V alentini G. Ensemble Clustering with a Fuzzy Approach[M]. [S. l.]: Springer, 2008.

[6] Karypis G, Han E H, Kumar V. CHANELEON: A Hierarchical Clustering Algorithm Using Dynamic Modeling[J]. Computer, 1999, 32(8): 68-75.

[7] Estivill C V, Lee I. AU TOCLUST: Automatic Clustering via Boundary Extraction for Mining Massive Point-data Sets[C]//Proc. of the 5th International Conference on Geocomputation. Greenwich, UK: [s. n.], 2000: 23-25.

[8] Elghazel H, Yoshida T, Deslandres V, et al. A New Greedy Algorithm for I mproving B-c oloring Clustering[J]. Lecture Notes in Computer Science, 2007, 45(38): 228-239.

[9] Li Yujian. A Clustering Algorithm Based on Maximal θ-distant Subtrees[J]. Pattern Recognition, 2007, 40(5): 1425-1431.

[10] von L uxburg. A Tutorial on Spectral Clustering[J]. Statistics and Computing, 2007, 17(4): 395-416.

[11] 鄭加明, 陳昭炯. 帶連通性約束的快速交互式Graph-Cut算法[J]. 計算機輔助設計與圖形學學報, 2011, 23(3): 399-405.

[12] Strandmark P, Kahl F. Parallel and Distributed Graph Cuts by Dual Decomposition[C]//Proc. of IEEE Conference on Computer V ision and Pattern Re cognition. San Francisco, USA: IEEE Press, 2010: 2085-2092.

[13] Candemir S, Akgul Y S. Adaptive Regularization Parameter for Graph Cut Segmentation[C]//Proc. of International Conference on Image Analysis and Recognition. Povoa de V arzim, Portugal: Springer, 2010: 117-126.

[14] James B O. A Faster Strongly Polynomial Time Algorithm for Submodular Function Minmization[J]. Mathematical Programming: Series A and B, 2009, 118(2): 237-251.

[15] Hartuv E, Shamir R. A Clustering Algorithm Based on Graph Connectivity[J]. Information Proce ssing Letters, 20 00, 76(4): 175-181.

編輯 任吉慧

Data Clustering Algorithm for DNA Microarray Based on Graph Theory

SONG Jia1,2, XU Li1, SUN Hong2

(1. Electrical Engineering College, Zhejiang University, Hangzhou 310027, China; 2. Department of Electronic and Information Engineering, Suzhou Vocational University, Suzhou 215104, China)

Clustering is an effective and practical method to mine the huge amount of DNA microarray data to gain important genetic and biological information. However, most traditional clustering algorithms can only provide a single clustering result, and are unable to identify distinct sets of genes with similar expression patterns. This paper presents an algorithm that can cluster D NA microarray data with a graph theory based algorithm. In particular, a DNA microarray dataset is represented by a graph whose edges are weighted, then an algorithm which can compute the minimum weighted and second minimum weighted graph cuts is applied to the graph respectively. Test results show that this approac h can achieve improved clustering accuracy, compared with other clustering methods such as Fuzzy-Max, Fuzzy-Alpha, Fuzzy-Clust.

microarray; gene expression data; clustering analysis; graph cut; graph theory; minimum cut

10.3969/j.issn.1000-3428.2014.05.008

江蘇省自然科學基金資助項目(BK2011319)；蘇州市職業大學青年基金資助項目(SZDQ09L02)。

宋 佳(1980－)，女，講師、博士研究生，主研方向：生物信息學，智能控制；許 力，教授；孫 洪，講師、博士。

2013-04-22

2013-05-22E-mail：sjia@jssvc.edu.cn

1000-3428(2014)05-0036-05

A

TP309