FI代數的模糊素MP濾子與模糊超MP濾子

劉春輝

1.赤峰學院 教務處，內蒙古 赤峰 024001

2.赤峰學院 數學與統計學院，內蒙古 赤峰 024001

FI代數的模糊素MP濾子與模糊超MP濾子

劉春輝

1.赤峰學院 教務處，內蒙古 赤峰 024001

2.赤峰學院 數學與統計學院，內蒙古 赤峰 024001

1 引言

Fuzzy蘊涵代數（簡稱：FI代數）是由我國學者吳望名于1990年提出的，作為對非經典邏輯代數中“蘊涵”連接詞的代數化，它揭示了各種邏輯蘊涵算子的共同本質[1]。眾多的邏輯代數系統，如MV代數（格蘊涵代數）、BL代數、R0代數（NM代數）、有界BCK代數以及剩余格等都可以看成是FI代數的特例，因此對FI代數結構的研究具有廣泛而基本的重要意義。迄今為止，有關這方面的研究工作已經獲得了很多有價值的研究成果[2-7]。

自從20世紀60年代美國著名的控制論專家Zadeh首次提出模糊集[8]的概念以來，模糊集的思想和方法已經被有效地應用于各個學科領域。近年來，國內外學者將這一思想和運算方法引入到邏輯代數的理想和濾子概念的研究，提出了多種形式的模糊理想和模糊濾子概念，并針對它們的特性和相互關系做了許多重要的研究工作，提出了大量有意義的研究課題并獲得了一批優秀的研究成果[9-14]。為了進一步揭示FI代數的結構特征，文獻[15]在FI代數中引入了多種模糊MP濾子概念，并對它們的性質和相互關系進行了細致的探討，以此為基礎，本文繼續對FI代數的模糊MP濾子概念作深入研究，引入模糊素MP濾子和模糊超MP濾子概念并考察其特性，獲得了一些有意義的結果。

2 預備知識

定義1[1]（Fuzzy蘊涵代數）（2，0）型代數(X，→，0)稱為Fuzzy蘊涵代數，簡稱FI代數，若 x，y，z∈X

FI-1：x→(y→z)=y→(x→z)；

FI-2：(x→y)→((y→z)→(x→z))=1；

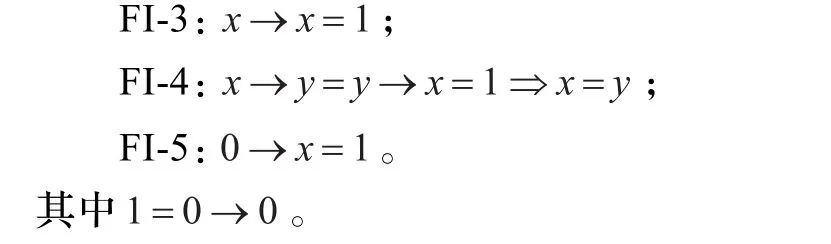
為了敘述簡潔，以下如無特別說明，X均表示FI代數。文獻[1]在 X上定義了一個偏序關系≤使得x≤y?x→y=1，?x，y∈X 。同時，定義一元運算 c:X→X 使得c(x)=x→0。

引理1[1]任意 x，y，z∈X，下列結論成立：

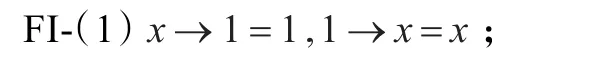
FI-（2）如果x≤y，則z→x≤z→y且y→z≤x→z。

定義2[7]設 X為FI代數，若(X，≤)構成并半格，即?x，y∈X，x∨y都存在，則稱 X為并半格FI代數。如果并半格FI代數X滿足：

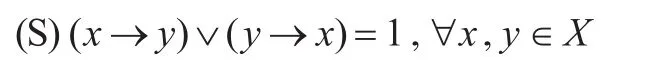
則稱X為滿足條件(S)的并半格FI代數。

引理2[4]設 X為并半格FI代數，則對任意的 x，y∈X，(x∨y)→y=x→y。

定義3[7]設?≠F?X，如果（1）1∈F 且（2）?x，y∈X，x，x→y∈F?y∈F，則稱 F是 X的 MP濾子。X 的全體MP濾子之集記為FMP(X)。

定義4[7]設X為一個并半格FI代數，X≠P∈FMP(X)，如果 ?x，y∈X，x∨y∈P蘊涵 x∈P或 y∈P，則稱 F 是X的素MP濾子。

引理3[7]設 X為滿足條件(S)的并半格FI代數，則X≠P∈FMP(X)是 X的素 MP濾子當且僅當?x，y∈X，x→y∈P或 y→x∈P。

引理4[7（]素MP濾子定理）設X為并半格FI代數，S?X對∨關閉，F∈FMP(X)且 F∩S=?。則存在 X的素MP濾子P使得F?P且P∩S=?。

引理5[7]設 X為并半格FI代數，如果 F∈FMP(X)且x?F。則存在X的素MP濾子P使得F?P且x?P。

定義5[9]非空集合X上的一個模糊集指的是映射μ:X→[0，1]。設 μ是 X上模糊集，稱集合 μt={x∈X| μ(x)≥ t}，?t∈[0，1]為 μ的 t截集。

設μ和v為非空集合 X上的兩個模糊集，定義 μ和v之間的模糊包含關系?如下：

μ?v當且僅當 μ(x)≤v(x)，?x∈X

定義6[15]設 X為FI代數，稱 X上的模糊集μ為X的模糊MP濾子，如果

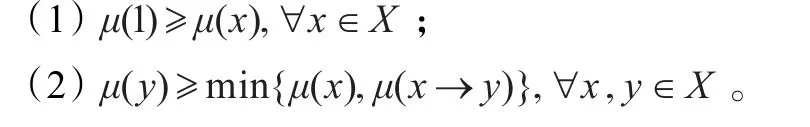
注1設 X為FI代數，μ為 X的模糊MP濾子，則x≤y蘊涵 μ(x)≤μ(y)，即 μ是保序的。

引理6[8]X上的模糊集μ為X的模糊MP濾子當且僅當 ?t∈[0，1]，μt=? 或 μt∈FMP(X)。

引理7[8]設 X為FI代數，則 X上的模糊集 μ為 X的模糊 MP濾子當且僅當 x→(y→z)=1蘊涵 μ(z)≥min{μ(x)，μ(y)}，?x，y，z∈ X 。

3 FI代數的模糊素MP濾子

定義7設 X為FI代數，μ為X的非常值的模糊MP 濾子。如果 ?t∈[0，1]，μt=? 或當 μt≠X 時，μt為X的素MP濾子，則稱μ為X的模糊素MP濾子。

定理1設X為并半格FI代數，則X的非常值模糊MP濾子μ為X的模糊素MP濾子當且僅當對任意的x，y∈X，μ滿足：

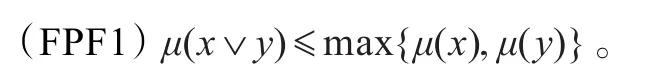
證明設μ是 X的非常值的模糊MP濾子且滿足條件（FPF1）。對任意的 t∈[0，1]，若 μt≠?，則由引理6可知 μt∈FMP(X)。若 μt≠X 且 x∨ y∈ μt，則 μ(x∨y)≥t，于是由（FPF1）知：

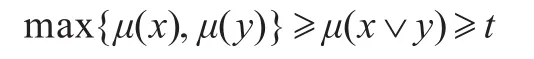
從而 μ(x)≥t或 μ(y)≥t，進而 x∈μt或 y∈μt，故由定義4知 μt為 X的素 MP濾子。因此 μ為 X的模糊素 MP濾子。

反之，設 μ為 X的模糊素 MP濾子。令t=μ(x∨y)，則 x∨y∈μt，故由引理6知 μt∈FMP(X)。若 μt=X，則x，y∈μt，從而 μ(x)≥t=μ(x∨y)且 μ(y)≥t=μ(x∨y)，因此max{μ(x)，μ(y)}≥μ(x∨y)。若 μt≠X，則由題設條件知 μt為 X的素 MP濾子。因此 x∨y∈μt蘊涵 x∈μt或 y∈μt，從而 μ(x)≥t=μ(x∨y)且 μ(y)≥t=μ(x∨y)，進而亦有max{μ(x)，μ(y)}≥μ(x∨y)。因此（FPF1）。

注2設X為并半格FI代數，μ為X的非常值的模糊MP濾子。則由模糊MP濾子的保序性可知定理1中的條件（FPF1）等價于：

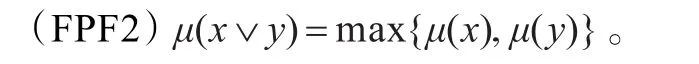
例1 設 X={0，a，b，1}且 0＜a＜b＜1，定義 X 上二元運算“→1”如表1所示。則利用如圖1所示的MATHEMATICA程序可驗證(X，→1，0)是一個FI代數。

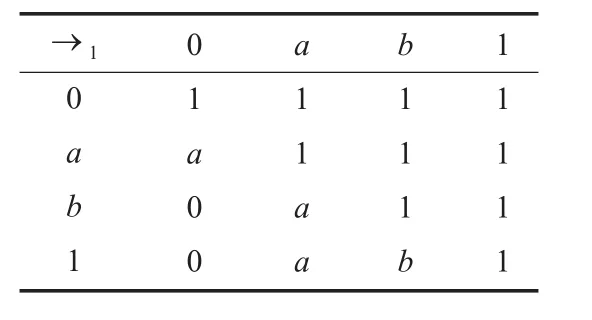
表1 運算“→1”的定義

在 X 上定義模糊集 μ使得 μ(0)=μ(a)=0.2，μ(b)= 0.4，μ(1)=0.6，則容易驗證 μ是 X的一個模糊素 MP濾子。

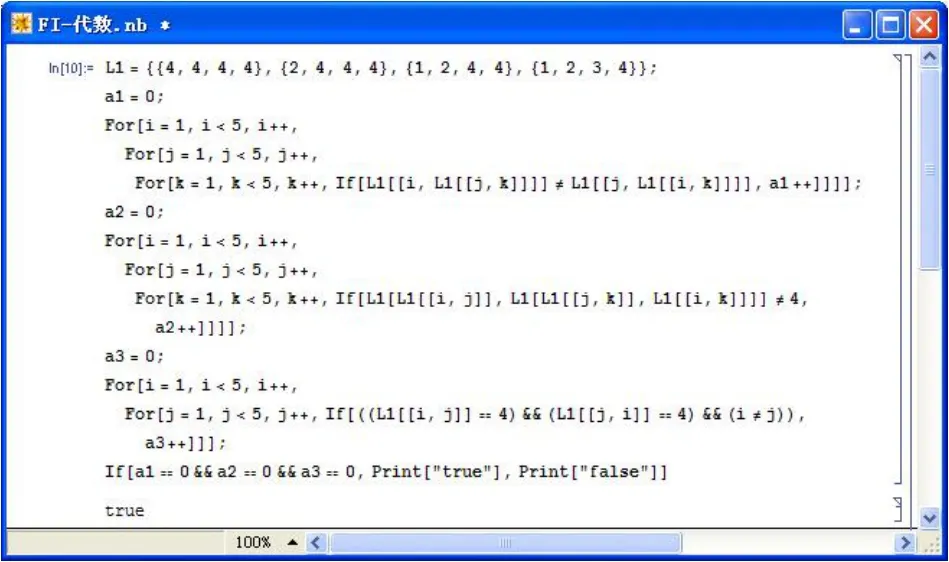
圖1 驗證FI代數的MATHEMATICA程序

定理2設X為并半格FI代數，則X的非常值模糊MP濾子μ為 X的模糊素MP濾子當且僅當μ(x∨y)= μ(1)蘊涵 μ(x)=μ(1)或 μ(y)=μ(1)，?x，y∈ X 。

證明設是 X的模糊素 MP濾子，x，y∈X使得μ(x∨y)=μ(1)，則由（FPF2）可知 max{μ(x)，μ(y)}=μ(x∨y)= μ(1)，因此 μ(x)=μ(1)或 μ(y)=μ(1)。

反 之 ，設 μ(x∨y)=μ(1)蘊 涵 μ(x)=μ(1)或 μ(y)= μ(1)。假設 μ(x∨y)＞max{μ(x)，μ(y)}，則 μ(x∨y)＞μ(x)且μ(x∨y)＞μ(y)，因此 當 μ(x∨y)=μ(1)時有 μ(x)＜μ(1)且μ(y)＜μ(1)，這與題設條件矛盾。因此（FPF1）成立，從而μ為X的模糊素MP濾子。

定理3設X為滿足條件(S)的并半格FI代數，則X的非常值模糊MP濾子μ為X的模糊素MP濾子當且僅當 Xμ為 X 的素 MP濾子。其中 Xμ={x∈X|μ(x)=μ(1)}。

證明 由 Xμ的定義，顯然 Xμ=μμ(1)。因為 μ是 X的非常值模糊 MP 濾子，所以 μ(0)＜μ(1)，從而 0?Xμ。又由1∈Xμ知 Xμ≠?，故由定義7得 Xμ為 X的素 MP濾子。

反之，設 Xμ為 X的素MP濾子。則由引理2和引理 3知 ?x，y∈X，(x∨y)→y=x→y∈Xμ或 (x∨y)→x= y→x∈Xμ。故 μ((x∨y)→y)=μ(1)或 μ((x∨y)→x)=μ(1)。因此由定義 6 可得 μ(x)≥min{μ((x∨y)→x)，μ(x∨y)}= μ(x∨y) 或 μ(y)≥min{μ((x∨y)→x)，μ(x∨y)}=μ(x∨y) 。故 μ(x∨y)≤max{μ(x)，μ(y)}成立，因此 μ 為 X 的模糊素MP濾子。

推論1設X為滿足條件(S)的并半格FI代數，則X的非常值模糊MP濾子μ為X的模糊素MP濾子當且僅當對任意 x，y∈X，μ(x→y)=μ(1)或 μ(y→x)=μ(1)。

證明由定理3知μ為X的模糊素MP濾子當且僅當 Xμ為 X的素 MP濾子，而由引理3知這當且僅當x→y∈Xμ或 y→x∈Xμ，再由 Xμ的定義知這當且僅當μ(x→y)=μ(1)或 μ(y→x)=μ(1)。

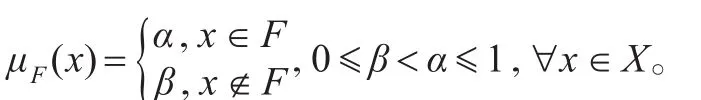
證明設 F∈FMP(X)為 X的素 MP濾子，則 F≠X，從而 μF不為常值。設 x，y∈X，由條件(S)知(x→y)∨(y→x)=1∈F，所以由引理3知 x→y∈F或 y→x∈F，即 μF(x→y)=α=μF(1)或 μF(y→x)=α=μF(1)。因此由推論1知 μF為 X的模糊素MP濾子。

反之，設μF為 X的模糊素MP濾子，則由定理3知F=XμF為 X的素MP濾子。

推論2設 X為滿足條件(S)的并半格FI代數，則F∈FMP(X)為 X的素MP濾子當且僅當 χF為 X的模糊素MP濾子。其中 χF為F的特征函數。

定理5（模糊素MP濾子的擴張定理）設X為滿足條件(S)的并半格FI代數，μ和v為 X的兩個模糊MP濾子，且滿足μ?v和 μ(1)=v(1)。如果 μ為 X的模糊素MP濾子，則v也是X的模糊素MP濾子。

證明因為μ為X的模糊素MP濾子，所以由推論1得 μ(x→y)=μ(1)或 μ(y→ x)=μ(1)。若 μ(x→y)=μ(1)，則由 μ?v和 μ(1)=v(1)可得 v(1)=μ(1)=μ(x→y)≤v(x→y)，從而可得 v(x→y)=v(1)。類似可證若 μ(y→x)=μ(1)，則v(y→x)=v(1)。因此由推論1便得v也是 X的模糊素MP濾子。

定理6設X為滿足條件(S)的并半格FI代數，μ為X的模糊素 MP濾子，k∈[0，μ(1))，則模糊集 μ∨k也是 X的模糊素 MP濾子。其中?x∈X，(μ∨k)(x)=max{μ(x)，k}。

證明首先證明μ∨k是 X的模糊MP濾子。任取x，y，z∈ X，設x→(y→ z)=1，則由引理7得μ(z)≥ min{μ(x)，μ(y)}，從而

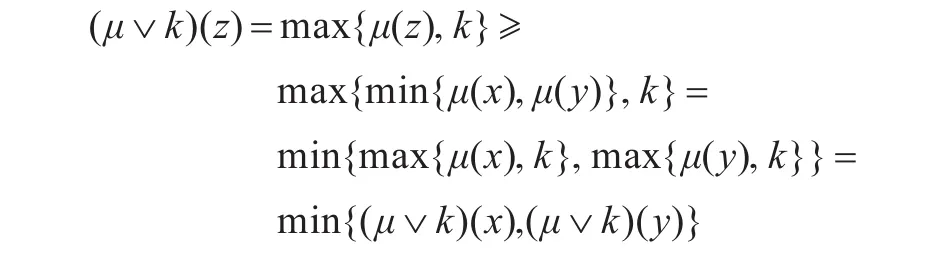
故再由引理7知μ∨k是X的模糊MP濾子。

其次證明μ∨k是X的模糊素MP濾子。因μ為X的模糊素 MP 濾子且 k＜μ(1)，故 (μ∨k)(1)=max{μ(1)，k}= μ(1)≠(μ∨k)(0)，否則 μ(1)=μ(0)，與 μ 非常值矛盾。又因為 ?x∈X，(μ∨k)(x)=max{μ(x)，k}≥μ(x)，所以 μ?(μ∨k)，再注意到 (μ∨k)(1)=μ(1)，由定理5便得 μ∨k是 X 的模糊素MP濾子。

定理7設X為滿足條件(S)的并半格FI代數，μ為X的非常值模糊MP濾子且μ(1)≠1。則存在X的模糊素MP濾子v使得 μ?v。

證明因為 μ為 X的非常值模糊 MP濾子，所以Xμ∈FMP(X)且 Xμ≠X。從而由引理5知存在 X的一個素MP濾子P使得Xμ?P。且由推論2又知 χP為X的模糊素 MP 濾子。令 v=χP∨k，其中 k=max{μ(x)|x∈XP}，則 k≤μ(1)＜1，因此由定理6知v為 X的模糊素 MP濾子且μ?v，?x∈X。從而定理得證。

定理8（模糊素MP濾子定理）設 X為滿足條件(S)的并半格FI代數，μ為 X的模糊 MP濾子，v為 X上的滿足條件 v(x∨y)=min{v(x)，v(y)}的模糊集，?k∈[0，μ(1))有 min{μ(x)，v(x)}≤k 。則存在 X 的模糊素 MP濾子 σ 使得 μ?σ 且 ?k∈[0，μ(1))，min{σ(x)，v(x)}≤k。

證明 ?k∈[0，μ(1))，令 S={x∈X|v(x)＞k}和 F={x∈X|μ(x)＞k} 。若 a，b∈S，則 v(a)＞k 且 v(b)＞k，從 而v(a∨b)=min{v(a)，v(b)}＞k，所以 a∨b∈S，這表明 S 對∨ 關閉。下證 F∈FMP(X)。事實上，由 ?k∈[0，μ(1))知μ(1)＞k，從而1∈F。設x，x→y∈F，則μ(x)＞k且μ(x→y)＞k，故 min{μ(x)，μ(x→y)}＞k，從而由 μ 為 X 的模糊 MP濾子知 μ(y)＞k，進而 y∈F，故 F∈FMP(X)。又因為由?k∈[0，μ(1))有 min{μ(x)，v(x)}≤k 可知 S∩F=?，所以由素MP濾子定理知存在X的素MP濾子P使F?P且 P∩S=?。令σ=χP∨k，則由定理6和推論2知σ為X的模糊素 MP濾子。若 x∈P，則σ(x)=max{1，k}= 1≥μ(x)。若 x?P，則 x?F，從而 μ(x)≤k=max{0，k}= σ(x)。因此總有 μ?σ。另一方面，若 x∈S，則x?F，從而 x? P，故 σ(x)=max{0，k}=k，于是 min{σ(x)，v(x)}= k。若 x?S，則 v(x)≤k，從而 min{σ(x)，v(x)}≤v(x)≤k。因此總有 ?k∈[0，μ(1))，min{σ(x)，v(x)}≤k 。

4 FI代數的模糊超MP濾子

定義8設 X為FI代數，μ為 X的非常值的模糊MP濾子。稱μ為 X的模糊超MP濾子，如果對任意的x∈X，μ滿足：

（FUF1）μ(x)=μ(1)或 μ(c(x))=μ(1)。

例2 設 X={0，a，b，c，d，1}，定義 X 上二元運算“→2”如表2所示。則利用如圖2所示的MATHEMATICA程序可驗證(X，→2，0)是一個FI代數。

表2 運算“→2”的定義

在 X上定義模糊集 μ使得 μ(1)=μ(a)=μ(d)=0.7，μ(0)=μ(b)=μ(c)=0.3，則容易驗證 μ是 X的一個模糊超MP濾子。

定理9設X為FI代數。則X的非常值的模糊MP濾子μ為X的模糊超MP濾子當且僅當μ滿足：

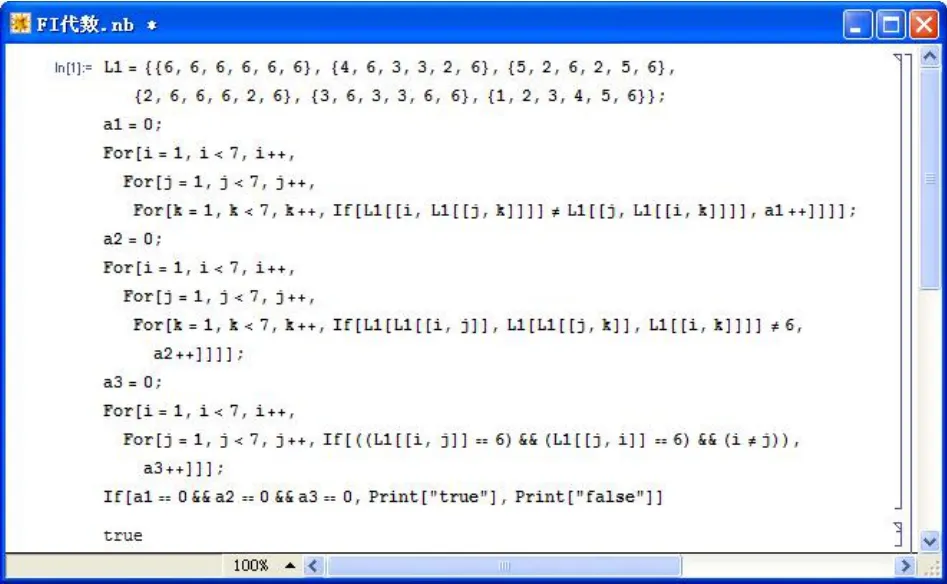
圖2 驗證FI代數的MATHEMATICA程序

（FUF2）μ(x)≠μ(1)且 μ(y)≠μ(1)蘊涵 μ(x→y)=μ(1)且 μ(y→x)=μ(1)，?x，y∈X 。

證明（FUF1）?（FUF2）：設 μ(x)≠ μ(1)且 μ(y)≠ μ(1)，因為 0≤y，所以 由 FI-（2）得 x→0≤x→y，即 c(x)≤x→y。于是由模糊 MP濾子 μ的保序性和（FUF1）得μ(x→y)≥μ(c(x))=μ(1)，因此 μ(x→y)=μ(1)。類似地，由μ(c(y))=μ(1)得 μ(y→x)=μ(1)。故（FUF2）成立。

（FUF2）?（FUF1）：設 μ(x)≠μ(1)，因為 μ為 X 的非常值模糊 MP 濾子，所以 μ(0)≠μ(1)，故由（FUF2）得μ(x→0)=μ(1)，即 μ(c(x))=μ(1)。因此由定義8知 μ 為 X的模糊超MP濾子。

定理10設X為滿足條件(S)的并半格FI代數。則X的非常值的模糊集μ為X的模糊超MP濾子當且僅當μ是X的模糊素MP濾子且滿足：

（FUF3）μ(x∨c(x))=μ(1)，?x∈X 。

證明“充分性”：設 μ是 X的模糊素MP濾子且滿足（FUF3）。設 x∈X，由注2可得 μ(x∨c(x))=μ(1)= max{μ(x)，μ(c(x))}。若 μ(x)≠μ(1)，因為由定義6知 μ(x)≤μ(1)且μ(c(x))≤ μ(1)，故由 μ(1)=max{μ(x)，μ(c(x))}得μ(c(x))= μ(1)。因此由定義8知μ為X的模糊超MP濾子。

“必要性”：設 μ為 X的模糊超 MP濾子。任取x∈X，因 為 x≤x∨c(x)且 c(x)≤x∨c(x)，故 由 注 1得μ(x)≤μ(x∨c(x))且 μ(c(x))≤μ(x∨c(x))。又由（FUF1）知μ(x)=μ(1)或 μ(c(x))=μ(1)，所以 μ(1)≤μ(x∨c(x))，因此再由定義6便得 μ(x∨c(x))=μ(1)，即（FUF3）成立。

?x，y∈X，因為x→((x→y)→y)=(x→y)→(x→y)=1且 y→((x→y)→y)=(x→y)→1=1，所以 x≤(x→y)→y且 y≤(x→y)→y，從而 x∨y≤(x→y)→y，因此由 μ的保序性可知 μ(x∨y)≤μ((x→y)→y)。又由 0≤y和FI-（2）得x→0≤x→y，進而(x→y)→y≤(x→0)→y=c(x)→y，因此 μ((x→y)→ y)≤μ(c(x)→ y)，故 μ(x∨y)≤μ(c(x)→ y)。如果 μ(x)=μ(1)，則 μ(x∨y)≤μ(1)=μ(x)≤max{μ(x)，μ(y)}。如果 μ(x)≠μ(1)，則由（FUF1）知 μ(c(x))=μ(1)，所以由定義6可 得 μ(y)≥min{μ(c(x))，μ(c(x)→y)}≥min{μ(1)，μ(c(x)→y)}=μ(c(x)→y)。因此可得 μ(x∨y)≤μ(y)≤max{μ(x)，μ(y)}。故由定義7又知μ是X的模糊素MP濾子。

5 結束語

本文將模糊集的思想和運算方法應用于FI代數的MP濾子理論的研究，引入了FI代數的模糊素MP濾子和模糊超MP濾子概念，并深入討論了它們的性質特征和相互關系。獲得了若干有意義的結論。值得注意的是，諸如MTL代數、R0代數（NM代數）、Heyting代數和MV代數（格蘊涵代數）等都可以看成是FI代數的自然擴張，從而，可以說上述結果是這諸多邏輯代數的共同特征的集中體現。因此，這些結論有助于在把握各種邏輯代數系統的個性特征的同時，也能認識到它們的共性特征和內在聯系。

[1] 吳望名.Fuzzy蘊涵代數[J].模糊系統與數學，1990，4（1）：56-64.

[2]李志偉，鄭崇友.Heyting代數與Fuzzy蘊涵代數[J].數學雜志，2002，22（2）：237-240.

[3]朱怡權，曹喜望.關于PFI代數與剩余格[J].數學進展，2006，35（2）：223-231.

[4]朱怡權.關于PFI代數的格論性質[J].四川師范大學學報：自然科學版，2007，30（2）：181-184.

[5]代建云，吳洪博.分配的Fuzzy蘊涵代數[J].模糊系統與數學，2008，22（1）：26-32.

[6]劉春輝.Fuzzy蘊涵代數及其拓撲[D].江蘇揚州：揚州大學，2008.

[7]劉春輝，徐羅山.Fuzzy蘊涵代數的素MP濾子[J].模糊系統與數學，2011，25（1）：32-37.

[8]裴道武，王三民，楊瑞.模糊蘊涵格理論[J].高校應用數學學報：A輯，2011，26（3）：343-354.

[9]Zadeh L A.Fuzzy sets[J].Information Control，1965，8：338-353.

[10]劉春輝.泛邏輯學中UB代數系統的(∈，∈∨q)-fuzzy濾子[J].計算機工程與應用，2009，45（34）：29-31.

[11]Liu L Z，Li K T.Fuzzy filters of BL-algebras[J].Information Science，2005，173（1/3）：141-154.

[12]Liu L Z，Li K T.Fuzzy implicative and Boolean filters of R0-algebras[J].Information Science，2005，171：61-71.

[13]肖云萍，鄒庭榮.泛邏輯學中UB代數系統的濾子與商代數[J].計算機工程與應用，2007，43（35）：90-92.

[14]肖云萍，鄒庭榮.泛邏輯學UB代數系統的fuzzy濾子[J].計算機科學與探索，2008，2（2）：212-216.

[15]劉春輝，徐羅山.FI代數的多種Fuzzy濾子[J].模糊系統與數學，2010，24（2）：21-27.

LIU Chunhui

1.Dean’s Office,Chifeng University,Chifeng,Nei Mongol 024001,China
2.College of Mathematics and Statistics,Chifeng University,Chifeng,Nei Mongol 024001,China

It applies the concept of fuzzy sets which introduced by Zadeh to FI-algebras,the notions of fuzzy prime MP filters and fuzzy ultra MP filters of FI-algebras are introduced,their properties and relations are discussed.Some equivalent characterizations of fuzzy prime MP filters in join semi-lattice FI-algebras with certain conditions are given.The fuzzy prime MP filters theorem of join semi-lattice FI-algebras is established.And the sufficient and necessary condition for an fuzzy set to be fuzzy ultra MP filters is obtained.

fuzzy logic;FI-algebra;fuzzy prime MP filter;fuzzy ultra MP filter

將Zadeh提出的模糊集概念應用于FI代數，提出了FI代數的模糊素MP濾子和模糊超MP濾子的概念并研究其性質及相互關系。給出了滿足一定條件的并半格FI代數的模糊素MP濾子的若干等價刻畫并建立了模糊素MP濾子定理。獲得了一個模糊集成為超模糊MP濾子的充要條件。

模糊邏輯；FI代數；模糊素MP濾子；模糊超MP濾子

A

O141.1；O153.1

10.3778/j.issn.1002-8331.1304-0221

LIU Chunhui.Fuzzy prime MP filters and fuzzy ultra MP filters in FI-algebras.Computer Engineering and Applications,2014,50（23）：77-81.

國家自然科學基金（No.10371106，No.60774073）。

劉春輝（1982—），男，講師，研究領域為非經典數理邏輯、Domain和拓撲學。E-mail：chunhuiliu1982@163.com

2013-04-15

2013-06-03

1002-8331（2014）23-0077-05

CNKI網絡優先出版：2013-06-26,http://www.cnki.net/kcms/detail/11.2127.TP.20130626.1542.021.html

◎網絡、通信、安全◎