模糊Hopfield網(wǎng)絡的收斂性與魯棒性分析

劉 亮，徐蔚鴻

長沙理工大學 計算機與通信工程學院，長沙 410114

模糊Hopfield網(wǎng)絡的收斂性與魯棒性分析

劉 亮，徐蔚鴻

長沙理工大學 計算機與通信工程學院，長沙 410114

1 引言

模糊Hopfield神經(jīng)是模糊神經(jīng)網(wǎng)絡的一個基本類別，是模糊系統(tǒng)和Hopfield神經(jīng)網(wǎng)絡的互補式結合。模糊神經(jīng)網(wǎng)絡的主要研究方向包括學習方法的設計、網(wǎng)絡結構優(yōu)化、容錯性、穩(wěn)定性及魯棒性等方面[1-6]。

近年來，眾多學者對模糊神經(jīng)網(wǎng)絡進行了廣泛研究，如劉普寅研究了Max-min模糊Hopfield神經(jīng)網(wǎng)絡的穩(wěn)定性與容錯性及學習算法[7]；徐蔚鴻研究了訓練模式對的攝動對模糊雙向聯(lián)想記憶網(wǎng)絡的影響及其控制[8]；Mehrnoosh Davanipoor提出了一種模糊小波神經(jīng)網(wǎng)絡的加速混合學習算法[9]；翟東海等提出了一種基于模糊神經(jīng)網(wǎng)絡的非線性系統(tǒng)的模型辨識方法[10]等。然而很少有對帶閾值模糊神經(jīng)網(wǎng)絡情況的相關問題進行研究。

本次首次引入了帶閾值的Max-T模糊Hopfield網(wǎng)

T 是映射 T:[0，1]2→[0，1]，T稱為T-模，是指其滿足以下4個條件：

（1）邊界性：?a∈[0，1]，aT1=a；

（2）交換律：?a，b∈[0，1]，aTb=bTa；

（3）結合律：?a，b，c∈[0，1]，aT(bTc)=(aTb)Tc；

（4）單調(diào)增：?a，b，c，d∈[0，1]，若 a≤c，b≤d ，則aTb≤cTd。

“?”是常規(guī)模糊關系合成運算，“?T”是∨-T型模絡模型，即將 n 個神經(jīng)元1，2，…，n 互聯(lián)，wij∈[0，1]表示神經(jīng)元i至 j的連接權值，在每個神經(jīng)元i處的閾值為ci。當輸入模式運行此網(wǎng)絡后，X(0)=(x1(0)，x2(0)，…，xn(0))∈[0，1]n網(wǎng)絡按下式演化：糊關系合成運算，W=(wij)n×n是[0，1]上的階連接權矩陣，wij為第i個和第 j個神經(jīng)元之間的連接權。

2 相關概念及引理

定義2.6[8]當模式對(A，B)發(fā)生攝動后被變?yōu)?A+ΔA，B)，且 H(A+ΔA，B)≤γ時，稱該模式對發(fā)生了最大前件γ攝動。當模式對(A,B)被變?yōu)?A,B+ΔB)，且H(A，B+ΔB)≤γ時，稱模式對發(fā)生了后件最大γ攝動；當模式 (A,B)被變?yōu)?(A+ΔA,B+ΔB)且 H(A+ΔA，A)∨H(B+ΔB，B)≤γ時，稱該模式對發(fā)生了最大γ攝動。

由于Hopfield網(wǎng)絡的本身特點，它的訓練模式不是成對出現(xiàn)的，因此它的訓練模式的攝動可以這樣定義：

定義2.7[12]當神經(jīng)網(wǎng)絡模型為模糊Hopfield網(wǎng)絡時，若模式 (A)攝動后變?yōu)?(A+ΔA)，且 H(A+ΔA，A)≤γ時，稱該模式發(fā)生了最大γ攝動。

定義2.8若對一切輸入 X∈[0，1]n，由式（1）定義的Max-T-C FHNN能經(jīng)過有限步迭代進入平衡點，則稱網(wǎng)絡具有良好的收斂性。

定義2.9假設Max-T-C模糊Hopfield神經(jīng)網(wǎng)絡采用學習算法 f，如果存在常數(shù)h＞0，對任意訓練模式集，set={Ak|k=1，2，…，p}和 γk＞0，k=1，2，…，p，當各模式(Ak)發(fā)生任意最大γ攝動致使set變成新訓練模式集合new_set，若對一切輸入 X∈[0，1]n，基于原訓練模式集該Max-T-C FHNN產(chǎn)生的輸出 ft(X，set)∈{[0，1]m|t∈T}，和基于攝動后的訓練模式集Max-T-C FHNN產(chǎn)生的輸出 ft(X，new_set)∈{[0，1]m|t∈T}總滿足 H(ft(X，set)，稱采用學習算法 f的該Max-T-C FHNN對訓練模式集全局擁有好的魯棒性（即Max-T-C FHNN不放大訓練模式集的最大攝動幅度）。其中 p代表任意模式數(shù)目。

引理2.1數(shù)學分析中Lipschitz條件是指：設g(a，b)是一個二元函數(shù)，D為定義域，若存在常數(shù)h＞0使得?X1=(a1，b1)，?X2=(a2，b2)∈D ，不等式 |g(X1)-g(X2)|≤h||X1-X2||則稱 g(a，b)在D上滿足Lipschitz條件（其中||·||是范數(shù)，它提示了函數(shù)值的變化與自變量的變化之間的一種關系）。

顯然若a,b,c,d在其定義域D上滿足|θ(a,b)-θ(c,d)|≤h(|a-c|∨|b-d|)成立，那么θ(a，b)在 D上滿足系數(shù)為h的Lipschitz條件。

3 Max-T-C模糊Hopfield網(wǎng)絡的收斂性及魯棒性分析

文獻[13]中提出了一種Max-T模糊Hopfield神經(jīng)網(wǎng)絡的通用的最大權值矩陣學習算法。

設 B={Bk|k∈K，Bk∈[0，1]n}是 Max-T FHNN 的穩(wěn)定態(tài)集，通用的最大權值矩陣學習算法步驟為：

第一步：對第k個模式Bk，計算臨時連接權矩陣；

第二步：用模糊交運算整合以上臨時矩陣，得到最終權值矩陣；

性質(zhì)1 設 set={Bk|k∈K，Bk∈[0，1]n}是模式集，則根據(jù)此學習算法所確定的連接權值學習矩陣W滿足：

性質(zhì)2 任意 set={Bk|k∈K，Bk∈[0，1]n}都可以成為Max-T-C FHNN網(wǎng)絡的平衡點集合。

定理3.1采用最大權值矩陣學習算法時，Max-T-C FHNN系統(tǒng)具有良好的收斂性。

設采用最大權值矩陣學習算法訓練網(wǎng)絡所得的權值矩陣為W ，C為閾值向量，A為初始狀態(tài)，系統(tǒng)在迭代一步后得到D，系統(tǒng)在迭代二步以后得到B。

顯然系統(tǒng)在迭代一步之后便進入了平衡狀態(tài)，所以Max-T-C FHNN具有良好的收斂性。

定理3.2采用最大權值學習算法時當T模及其蘊含算子R滿足Lipschitz條件時，Max-T-C FHNN對訓練模式集攝動全局擁有好的魯棒性。

證明由于T模及其蘊含算子R滿足Lipschitz條件，故有：

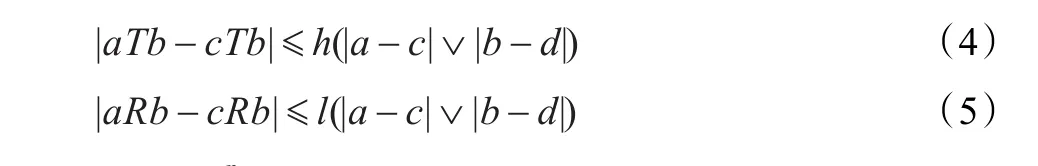
4 實驗

以下給出了基于最大權值矩陣學習算法訓練Max-T-C模糊Hopfield神經(jīng)網(wǎng)絡進行自聯(lián)想實驗，驗證該模型的收斂性及分析采用最大權值矩陣學習算法時，訓練模式集的攝動對網(wǎng)絡的影響。實驗采用大小為256×256的灰度圖像，選用直積(П)T-模，顯然此模滿足Lipschitz條件，其運算為TП(a，b)=ab，相應的模糊蘊涵算子根據(jù)定義有 aRПb=1，a≤b；aRПb=b/a，a＞b。

實驗步驟：

（1）取標準庫灰度圖像 Lena（見圖 1（a）），大小為256×256作為攝動前訓練模式集。把每h個像素的灰度值在歸一化處理后構成n個訓練模式，n=256/h×256。基于這些模式訓練網(wǎng)絡得到FHNN1。

圖1 訓練、輸入圖像

（2）將圖1（a）的某些像素點減去一個微小量，且在頂部及底部增加一條比較小的黑色線條，得到攝動后的圖像（見圖1（b））。同樣作為訓練模式集，訓練網(wǎng)絡得到FHNN2。

（3）取一幅不同于圖1（a）與圖1（b）的新圖像（見圖1（c）），將其分割成n個子圖像，并分別作為FHNN1的輸入，得到n個輸出，將其構成圖2（a），并記錄總的迭代次數(shù) I1；同樣將圖1（b）分割后作為Max-T-C FHNN2的輸入圖像，分別得到n個輸出，將其構成圖2（b），記錄總的迭代次數(shù)I2。

（4）圖3（a）為兩個訓練模式集圖像的差異，圖3（b）為兩個輸出結果的差異，越黑的點表示在相應點處的灰度值差異越小，此處取h=128。

圖2 輸出圖像

圖3 比較圖像

實驗采用了相同的網(wǎng)絡模型、相同的學習方法以及相同的輸入，只有訓練模式集存在小幅的差異。由實驗結果可知，F(xiàn)HNN1與FHNN2的迭代次數(shù)均為512，時間復雜度亦均為O(n)，驗證了所提出的網(wǎng)絡模型具有良好的收斂性。根據(jù)圖3可知，訓練模式集的攝動引起了模型的輸出差異，同時輸出差異小于訓練模式集的攝動差異，驗證了該網(wǎng)絡模型對訓練模式的攝動具有全局不放大性質(zhì)。

5 結論與展望

不確定性知識環(huán)境下獲取的模式容易出現(xiàn)小幅誤差。訓練模式的攝動和輸入模式的攝動將引起模糊神經(jīng)網(wǎng)絡的輸出攝動甚至大幅變化，從而對網(wǎng)絡多種性能和實用性可能產(chǎn)生嚴重副作用。嚴格證明了Max-T-C FHNN模型具有良好的收斂性及訓練模式攝動全局不放大性質(zhì)，對不確定知識環(huán)境下獲取模式具有重要指導意義。

同時，在Max-T-C FHNN聯(lián)想過程中，特別是在輸入模式存在誤差或畸變的條件下，分析模型能否聯(lián)想出正確的模式是接下來值得研究的非常有意義的課題。

[1]Pizzileo B，Li Kang.Improved structure optimization for fuzzy-neural networks[J].IEEE Transactions on Fuzzy Systems，2012，20（6）：1076-1089.

[2]Zhang Huaguang，Liu Jinhai.Data-core-based fuzzy Min-Max neural network for pattern classification[J].IEEE Transactions on Neural Networks，2011，22（12）：2339-2352.

[3]Li Hongyi，Chen Bing，Zhou Qi.Robust stability for uncertain delayed fuzzy Hopfield neural networks with Markovian jumping parameters[J].IEEE Transactions on Systems Man and Cybernetics，2009，39（1）：94-102.

[4]張義榮，劉普寅，鮮明，等.基于一類T-模的模糊Hopfield網(wǎng)絡的穩(wěn)定性分析[J].電子學報，2002，30（1）：30-33.

[5]徐蔚鴻，陳國平，楊靜宇，等.規(guī)則攝動時模糊蘊涵算子對模糊推理的魯棒性的影響[J].計算機學報，2005，28（10）：1700-1707.

[6]舒桂清，肖平.模糊聯(lián)想記憶網(wǎng)絡的增強學習算法[J].電子學報，2003，8（1）：84-89.

[7]Liu Puyin.Max-min fuzzy Hopfield neural networks and an efficient learning algorithm[J].Fuzzy Sets and Systems，2000，112（20）：41-49.

[8]徐蔚鴻，宋鸞姣，李愛華.訓練模式對的攝動對模糊雙向聯(lián)想記憶網(wǎng)絡的影響和控制[J].計算機學報，2006，29（2）：337-344.

[9]Davanipoor M，Zekri M，Sheikholeslam F.Fuzzy wavelet neural network with an accelerated hybrid learning algorithm[J].IEEE Transactions on Fuzzy Systems，2012，20（3）：463-469.

[10]翟東海，李力，靳蕃，等.一種基于模糊神經(jīng)網(wǎng)絡的非線性系統(tǒng)模型的辨識[J].計算機學報，2004，27（4）：561-565.

[11]張義榮，劉普寅.離散Hopfield神經(jīng)網(wǎng)絡的穩(wěn)定性研究[J].電子學報，2002，30（1）：30-33.

[12]宋丹.一類模糊Hopfield神經(jīng)網(wǎng)絡的攝動性質(zhì)及其應用[D].長沙：長沙理工大學，2007.

[13]曾水玲，楊靜宇，徐蔚鴻.一種模糊Hopfield網(wǎng)絡的學習算法及性質(zhì)[J].計算機科學，2010，37（12）：206-208.

[14]Repley B D.模式識別與神經(jīng)網(wǎng)絡[M].北京：人民郵電出版社，2009.

[15]王士同.神經(jīng)模糊系統(tǒng)及其應用[M].北京：北京航空航天大學出版社，1998.

LIU Liang,XU Weihong

College of Computer&Communication Engineering,Changsha University of Science and Technology,Changsha 410114,China

Convergence and robustness are two important properties of fuzyy neural network.This paper analyses the convergence and robustness of Max-T fuzzy Hopfield neural network with threshold（called Max-T-C FHNN）in the condition of perturbations of training patterns,which is proved theoretically.It is discovered that Max-T-C FHNN using maximum weight matrix is of excellent convergence.Max-T-C FHNN holds good robustness globally to perturbations of training patterns in the case that T-norms and its implication operator satisfy the Lipschitz condition.The self-association experiment is given to testify the theoretical results.

threshold;fuzzy neural network;Max-T fuzzy Hopfield neural network;convergence;robustness

收斂性與魯棒性是模糊神經(jīng)網(wǎng)絡的兩個重要性質(zhì)。對帶閾值的Max-T模糊Hopfield神經(jīng)網(wǎng)絡（記為Max-T-C FHNN）的收斂性及在訓練模式小幅攝動情況下的魯棒性進行了分析，從理論上給出了嚴格的證明。發(fā)現(xiàn)了采用最大權值矩陣學習算法時，Max-T-C FHNN具有良好的收斂性，同時當T模及其蘊含算子滿足Lipschitz條件時，Max-T-C FHNN對訓練模式攝動全局擁有好的魯棒性，用自聯(lián)想實驗驗證了理論的有效性。

閾值；模糊神經(jīng)網(wǎng)絡；Max-T模糊Hopfield神經(jīng)網(wǎng)絡；收斂性；魯棒性

A

TP18

10.3778/j.issn.1002-8331.1212-0246

LIU Liang,XU Weihong.Convergence and robustness analysis of fuzzy Hopfield neural network.Computer Engineering and Applications,2014,50（23）：73-76.

教育部重點科研項目（No.208098）；湖南省科技計劃項目（No.2012FJ30052）。

劉亮（1987—），男，碩士研究生，主要研究方向：計算智能、模式識別；徐蔚鴻（1963—），男，博士，教授，主要研究方向：智能系統(tǒng)、模式識別、軟件工程。E-mail：figolNew@163.com

2012-12-20

2013-02-21

1002-8331（2014）23-0073-04

CNKI網(wǎng)絡優(yōu)先出版：2013-03-21，http://www.cnki.net/kcms/detail/11.2127.TP.20130321.0939.002.html