基于區域序列枚舉法的蜂巢數獨求解算法研究

肖華勇，楊菲菲，黃奔茹

西北工業大學 理學院 數學系，西安 710129

基于區域序列枚舉法的蜂巢數獨求解算法研究

肖華勇，楊菲菲，黃奔茹

西北工業大學 理學院 數學系，西安 710129

1 引言

數獨（Sudoku）是一種基于邏輯推理的數學謎題，是18世紀末由瑞士數學家歐拉發明的，后在美國發展，并在日本得以發揚光大。數獨的玩法邏輯上非常簡單，但數字排列方式千變萬化。謎題中會預先填入若干數字，其他宮格為空白，玩家需要根據謎題中的數字分布狀況，邏輯推敲出剩余的空格所需數字。隨著對數獨研究的深入，出現了越來越多的變形，數獨形狀變化（蜂巢數獨、環狀數獨等）和引入和式計算（Killer數獨、Kakuro數獨等）等[1]。

蜂巢數獨是標準數獨形狀發生變化的數獨，其外形類似蜂巢，所以稱為蜂巢數獨。如圖1所示，蜂巢數獨有行，沒有列和九宮格，但有正斜線、反斜線。它要求每行、正斜線、反斜線所填數字不能重復，且每行、正斜線、反斜線所填數字序列是連續數列（例如 1～6，3～8，4～9，…）。除了中間的行、正斜線、反斜線所填數字是1～9，其他行、正斜線、反斜線所填數字不一定是從1開始，也就是說其他行、正斜線、反斜線所填數字不一定包括1～9這9個數字。由于蜂巢數獨并沒有九宮，最特殊的是蜂巢連線（行、正斜線、反斜線）數字序并不固定，所以不能完全沿用傳統數獨解題技法。

國內外學者針對數獨求解方面展開了大量研究，他們把數獨問題轉化成不同的數學模型。A.C.Bartlett等[2-3]針對對角線數獨、金字塔數獨等特殊形式的數獨建立了0-1整數規劃模型，并運用Matlab中的優化函數求得模型的解。肖華勇等[4]提出了用數獨規則的逐步枚舉算法求解標準數獨，該方法比回溯法具有更快的速度。Christian Posthoff等[5]用建立邏輯方程的形式求解數獨謎題，但是這種算法的效率比較低。劉延風等[6]用遺傳算法求解標準數獨。Sheehan Khan等[7]用概率圖解方法求解數獨，但是其算法的適應性、通用性不高。J. Goldberger[8]對信息傳遞算法進行了改進，使之適用于一般的數獨問題。Lynce等[9]用兩種SAT推理方法解決了數獨謎題。J.A.Bondy等[10]將數獨問題轉化為著色問題。肖華勇等[11]研究了標準數獨的方程求解算法問題。R.Lewis[12]提出利用現代優化算法求解標準數獨問題，并提出了一種基于模擬退火的求解方法。但是以上文獻多針對標準數獨展開研究，而對于蜂巢數獨等變形數獨的研究較少。

圖1 初級蜂巢數獨謎題

目前國內外學者對于蜂巢數獨的研究多局限于行列唯一法、基本摒除法、三角形摒除法、余數法、數偶法、砂漏法等直觀法求解[13]，與標準數獨的直觀法求解[14]有很大的不同。但是對計算機求解蜂巢數獨的算法的研究尚屬起步階段。

蜂巢數獨同標準數獨最大的區別在于形狀類似蜂巢，完全拋棄了九宮格，對序列有連續性的要求。因此在求解算法上，兩者相似但有很大的不同。本文利用線性規劃方程組建立數學模型，研究其解的性質，然后提出算法，并用實例說明求解的有效性。

2 線性規劃模型的建立

2.1 單元格的表示

蜂巢數獨的行對應標準數獨的行，正斜線表示數獨從左到右從右上到左下的9條斜線，反斜線表示數獨從左到右從左上到右下的9條斜線。

每個單元格用坐標(i，j)表示。i代表行號，從上到下 i=1，2，…，9 ；j代表列號，從左到右為 1，2，3，… 。其中第1行 j=1，2，…，5，第2行 j=1，2，…，6，依次類推，第9行 j=1，2，…，5。

用 Ai(i=1，2，…，9)表示每行存放的單元格的集合 。其 中 A1={(1，1)，(1，2)，(1，3)，(1，4)，(1，5)}，A2={(2，1)，(2，2)，(2，3)，(2，4)，(2，5)，(2，6)}，以此類推 A9={(9，1)，(9，2)，(9，3)，(9，4)，(9，5)}。

用Bi(i=1，2，…，9)表示每條正斜線存放的單元格的集合，每條正斜線上的單元格按從上到下排列。

其 中 B1={(1，1)，(2，1)，(3，1)，(4，1)，(5，1)}，B2={(1，2)，(2，2)，(3，2)，(4，2)，(5，2)，(6，1)} 以此類推 B9={(5，9)，(6，8)，(7，7)，(8，6)，(9，5)}。

用Ci(i=1，2，…，9)表示每條反斜線存放的單元格的集合，每條反斜線上的單元格按從上到下排列。

其 中 C1={(5，1)，(6，1)，(7，1)，(8，1)，(9，1)}，C2={(4，1)，(5，2)，(6，2)，(7，2)，(8，2)，(9，2)}，以此類推 C9={(1，5)，(2，6)，(3，7)，(4，8)，(5，9)}。

每個單元格有其所在的行號，正斜線號和反斜線號。每個單元格用一個三維向量(u，v，w)表示。如單元格 (1，1)的三維向量為 (1，1，5)，它表示單元格 (1，1)是第1行，第1條正斜線和第5條反斜線相交的單元格。

2.2 區候選數的確定

由于除了中間的行、正斜線、反斜線所填數字是1～9，其他行、正斜線、反斜線所填數字不一定包括1～9這9個數字。所以它不能像標準數獨那樣讓空單元格的初始候選數取1～9這9個數字，它要按各行所含有的單元格數和已填數字來確定初始候選數。

為方便起見，把某行、某正斜線、某反斜線都稱為一個區。設某區有L個格子，則該區只允許L個連續數字。若該區所填數字單元格大于1個時，取所填數字中最小數字為a，最大數字為b；若該區所填數字單元格只有一個時，a取該單元格的值，且b=a；則該區候選數范圍為 [m，M]，其中 m=max{1，b-L+1}，M=min{9，a+L-1}。當該區一個數字也沒有填，取m=1，M=9。由于該區所填數字是L個連續數字，這連續數字序列可能為 [m，m+L-1]，或 [m+1，m+L]，…，或 [M-L+1，M]，則該區必然出現的候選數為這些連續數字序列的交集[M+(1-L)，m+(1-L)]。各區必然出現的候選數用L(At)，L(Bt)，L(Ct)表示，其中 t=1，2，…，9 。

如圖1，第一行 a=6，b=7，L=5，則第一行候選數范圍為 [3，9]，5 個連續數字序列可能為 [3，7]，或 [4，8]，或[5，9]，第一行必然出現的候選數為{5，6，7}，即 L(A1)= {5，6，7}。

2.3 單元格候選數的確定

若某個單元格所在行、正斜線、反斜線得到的候選數范圍為 [m1，M1]，[m2，M2]，[m3，M3]，則該單元格的初始候選數為[d，u]，其中 d=max{m1，m2，m3}，u=min{M1，M2，M3}。

如圖1，單元格 (1，1)的三維向量為 (1，1，5)，它所在第一行中 a=6，b=7，L=5，則第一行候選數范圍為[3，9]；它所在第一條正斜線中 a=3，b=6，L=5，則第一條正斜線候選數范圍為[2，7]；它所在第五條反斜線中a=2，b=8，L=9，則第五條反斜線候選數范圍為 [1，9]；那么單元格 (1，1)的初始候選數為3，4，5，6，7。

2.4 建立決策變量

為表達方便，設所有解未確定的變量都取xijk=-1，表示數字k為格子(i，j)的候選數。

3 線性規劃方程組的性質

3.1 候選數刪除性質

性質3.1.1若 xijk=1，則 xijl=0，l≠k 。當格子 (i，j)的數字確定時，利用該性質可刪除該格子上的其余候選數。

性質 3.1.2若 xijk=1，則 xilk=0，(i，j)∈ At，(i，l)∈ At，l≠j，t=1，2，…，9 。當格子 (i，j)的數字確定為 k 時，利用該性質可刪除該格子所在第t行區其他格子上的候選數k。

性質 3.1.3若 xijk=1，則 xmnk=0，(i，j)∈ Bt，(m，n)∈Bt，(i，j)≠(m，n)，t=1，2，…，9 。當格子 (i，j)的數字確定為k時，利用該性質可刪除該格子所在第t正斜線區其他格子上的候選數k。

性質 3.1.4若 xijk=1，則 xmnk=0，(i，j)∈ Ct，(m，n)∈Ct，(i，j)≠(m，n)，t=1，2，…，9 。當格子 (i，j)的數字確定為k時，利用該性質可刪除該格子所在第t反斜線區其他格子上的候選數k。

3.2 確定性性質

為表示方便，建立函數：

性質3.2.2若 xijk=-1，k∈[M+1-L，m-1+L]對任意的 (m，n)∈ At，(i，j)∈ At，(i，j)≠(m，n)，都有 xmnk≠ -1，則必有xijk=1。該性質表示當該格子在第t行區存在必定出現的數字，并且第t行區的其他格子未存在時，該格子所填數字必為候選數k。

性質3.2.3若 xijk=-1，k∈[M+1-L，m-1+L]對任意的 (m，n)∈Bt，(i，j)∈Bt，(i，j)≠(m，n)，都有 xmnk≠-1，則必有xijk=1。該性質表示當該格子在第t正斜線區存在必定出現的數字，并且第t正斜線區的其他格子未存在時，該格子所填數字必為候選數k。

性質3.2.4若 xijk=-1，k∈[M+1-L，m-1+L]對任意的 (m，n)∈ Ct，(i，j)∈ Ct，(i，j)≠(m，n)，都有 xmnk≠ -1，則必有xijk=1。該性質表示當該格子在第t反斜線區存在必定出現的數字，并且第t反斜線區的其他格子未存在時，該格子所填數字必為候選數k。

3.3 矛盾性質

性質3.3.1若對某固定格子(i，j)，對任意數字k，都有 xijk=0或1。若則導致該數獨矛盾。該性質表明任何一個格子所填的數只能有1個。

性質3.3.2若對某固定區t及數字k，對任意格子(i，j)∈At都有xijk=0 或 1。若2，…，9)，則導致該數獨矛盾。該性質表明任何一個數在任何一個行區只能填1次。

性質3.3.3若對某固定區t及數字k，對任意格子(i，j)∈Bt，都有xijk=0 或 1。若2，…，9)，則導致該數獨矛盾。該性質表明任何一個數在任何一個正斜線區只能填1次。

性質3.3.4若對某固定區t及數字k，對任意格子(i，j)∈Ct，都有xijk=0 或 1。若2，…，9)，則導致該數獨矛盾。該性質表明任何一個數在任何一個反斜線區只能填1次。

3.4 不變性

性質 3.4.1對某固定格子 (i，j)，若 xijk=-1，k∈{m，m+1，…，M}，即格子 (i，j)候選數為 m，m+1，…，M 。對所有候選數k，當 xijk=1時，某個格子(p，q)都不能填r，則xpqr=0。對某個候選數k，當xijk=1時導致數獨矛盾，則必有xijk=0。

性質 3.4.2對某 r(r=2，3，4，…)個固定格子 (i1，j1)，(i2，j2)，…，(ir，jr)，若 xi1j1k1=-1，k1∈{m1，m1+1，…，M1}，…，xirjrkr=-1，kr∈{mr，mr+1，…，Mr} 。即格子 (i1，j1)的候選 數為 m1，m1+1，…，M1，格子 (ir，jr) 的候選數為 mr，mr+1，…，Mr。當對r個格子的多有候選數來說，當xi1j1k1=-1，…，xirjrkr=-1時，某個格子 (i，j)都不能填 r，則xijr=0。

4 算法應用及實例計算

綜合前面由線性規劃方程組得到的四類性質，本文提出求解該方程組的算法。

初始化：將數獨謎題存放在數組T[9][9]中，若格子(i，j)為空格，則令 T[i][j]=0 ；若格子 (i，j)已填入數字k，則令T[i][j]=k。基于蜂巢數獨獨特的形狀，為了保證數組的完整性，其他未有格子的部分填-1。將數獨格子的候選數存放在數組x[9][9][9]中，同樣地，若格子(i，j)為空格，則令 x[i][j][k]=-1，k=1，2，…，9 ；若格子(i，j)已填入數字 k，則令 x[i][j][k]=1，x[i][j][l]=0(l≠k)。

步驟1根據2.3節的方法確定每個格子的候選數，然后根據3.1節性質進行候選數的刪除。

步驟2根據3.2節性質確定性對數獨進行填寫，若完整則程序結束，否則進入下一步。

步驟3對格子進行單區枚舉，刪除每個區中各格子的候選數。對任意一個區進行滿足連續序列的枚舉。將引起矛盾的候選數組合刪除，記錄沒有引起矛盾的候選數組合及由前面推理得到的新的候選數表，將得到的所有候選數表求并，從而得到各空格新的候選數集。實現刪除候選數的目標。

步驟4利用每個區各格子新的候選數集，刪除其他相關格子中的候選數。

步驟5若數獨未填寫完整，轉入步驟3，若填寫完整，程序結束，輸出結果。

步驟6對格子進行兩區枚舉，刪除兩個區中各格子的候選數。對任意兩個區進行滿足連續序列的枚舉，然后進行同步驟3相同的處理。

步驟7若數獨未填寫完整，轉入步驟4，若填寫完整，程序結束，輸出結果。

對圖1利用候選數刪除和確定操作之后，空格減少了6個，如圖2所示。再進行一次單區枚舉后，數獨已經完成，如圖3所示。

圖2 確定性操作結果

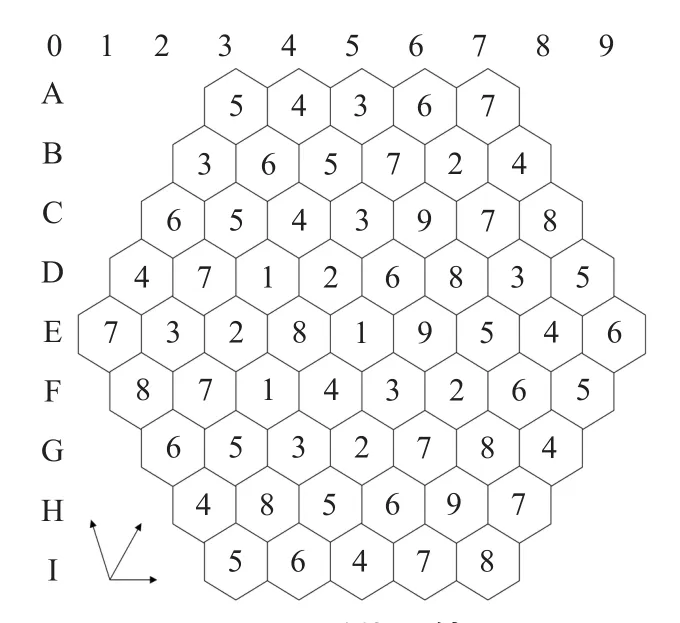
圖3 單區枚舉結果

再如，對圖4所示的中級謎題，進行文獻[11，15]中的空格枚舉算法同本文提出的區域序列枚舉法對比實驗。結果顯示，空格枚舉算法中，當枚舉空格數增大到4的時候，還是無法求解出此謎題。然而當采用本文提出的區域序列枚舉算法時，謎題結果如圖5所示。進行確定及空格枚舉操作后，空格數同樣也并未減少，選取第9行區進行枚舉，符合的連續序列有：34567和45678，將這兩組序列進行已知數4和7的排列組合，符合它的序列有12種，如：37546，37645等等。經過單區序列枚舉得到結果圖5所示。

圖4 中級蜂巢數獨謎題

圖5 中級蜂巢區序列枚舉結果

經過同文獻[11]中提出的算法進行對比實驗，得出少量的初級蜂巢數獨謎題只需空格枚舉就可以完成，對于中級甚至高級謎題，單空格枚舉和多空格枚舉失效，但是采用序列的區域枚舉就可以完成。這就體現出了蜂巢數獨其獨特的規則，即序列的連續性。這是它和標準數獨在算法上面的不同點。

5 結論

本文提出的對蜂巢數獨問題的方程組求解算法，利用了數獨問題對應的方程的性質進行候選數的刪除和更新，實現了由空格枚舉[11，15]向序列枚舉的轉變。對絕大多數的數獨問題，用很少格子的枚舉就能實現求解，而且計算時間都在毫秒級。但是這種空格枚舉的方法只能針對初級及極少數中級的蜂巢數獨謎題，當空格數少于8個甚至更少的時候，這種空格枚舉方法的作用就很小了，于是區序列枚舉算法就起到了至關重要的作用。但是本文提出的算法即使再使用多區序列枚舉后，高級蜂巢數獨謎題的實現效率依然很低，同時當蜂巢數獨需要經過同時枚舉幾個區才能獲得時速度比較慢，可以考慮改進的方法。這將是下一步將要做的工作。

[1]Garns H.Number place[J].Dell Pencil Puzzles&Word Games，1979，16（5）.

[2]Bartlett A，Chartier T P，Langville A N，et al.An integer programming modelforthesudoku problem[EB/OL].（2006-03-10）.http：//www.cofc.edu/langvillea/Sudoku/sudoku2.pdf.

[3]Simons F.Solving a sudoku puzzle with mathematica[J]. Mathematica in Education and Research，2005，10（4）：1-24.

[4]肖華勇，田錚，馬雷.數獨基于規則的逐步枚舉算法設計[J].計算機工程與設計，2010，31（5）：1035-1037.

[5]Posthoff C，Steinbach B.Sudoku solutions using logic equations[Z].2008.

[6]劉延風，劉三陽.基于遺傳算法求解數獨難題[J].計算機科學，2010（3）：225-226.

[7]Khan S，Jabbar S，Jabbari S，et al.Solving sudoku using probabilistic graphical models[Z].2009.

[8]Goldberger J.Solving sudoku using combined message passing algorithms[Z].[S.l.]：School of Engineering，Bar-llan University，2007.

[9]Lynee I，Ouaknin J.Sudoku as a SAT problem[C]//Proc of the 9th International Symposium on Artificial Intelligence and Mathematics，2006.

[10]Bondy J A，Murty U S R.Graph theory with applications[M].London：Macmilian，1976.

[11]肖華勇，程海礁，王月興.九宮數獨的方程求解算法研究[J].計算機應用，2012，32（10）：2907-2910.

[12]Lewis R.Metaheuristics can solve sudoku puzzles[J].Journal of Heuristics，2007，13：387-401.

[13]直觀法玩數獨——SUDOKU[EB/OL].[2012-10-20].http：// hi.baidu.com/kiwy07/item/2e00ad1665e41458f0090e0b.

[14]Lei Lei，Shen Fuke.The design and implementation of the algorithm about sudoku[J].Computer Knowledge and Technology，2007，2：481-482.

[15]肖華勇，馬麗娜，程海礁.老板數獨的方程求解算法研究[J].計算機工程與應用，2014，50（9）：41-44.

XIAO Huayong,YANG Feifei,HUANG Benru

Department of Mathematics,School of Science,Northwestern Polytechnical University,Xi’an 710129,China

Honeycomb sudoku is a kind of deformation of sudoku which is similar to the honeycomb and difficult to solve.Section 1 of the full paper presents the linear programming equation set equivalent with the honeycomb sudoku puzzle. Section 2,the properties of the solution algorithm of honeycomb sudoku are derived from the equation set,such as the property of removing the candidate numbers,the contradictoriness,the unique certainty and the invariance of enumeration.Section 3 solves the honeycomb sudoku with a regional sequence enumeration method,and the difference of solving algorithm between the honeycomb sudoku and standard sudoku is compared.The proposed algorithm is proved effective for the honeycomb sudoku of medium level by examples.

honeycomb sudoku;deformation of sudoku;equation set;regional sequence enumeration method

蜂巢數獨是類似蜂巢難度又高的變形數獨，它有著重要的研究意義。由蜂巢數獨謎題提出與之等價的線性規劃方程組；從方程組出發推導出求解數獨算法的性質，如候選數刪除性質、矛盾性質、唯一確定性質、枚舉不變性質；基于以上性質，提出用區域序列枚舉方法求解蜂巢數獨。結合實例計算，提出的算法對中度難度級別的蜂巢數獨是有效的。

蜂巢數獨；變形數獨；方程組；區域序列枚舉

A

O157

10.3778/j.issn.1002-8331.1305-0513

XIAO Huayong,YANG Feifei,HUANG Benru.Equation model for honeycomb sudoku based on regional sequence enumeration method.Computer Engineering and Applications,2014,50（23）：36-40.

西北工業大學2013大學生創新項目基金（No.07gz1601）。

肖華勇（1969—），男，博士，副教授，主要研究方向：統計優化；楊菲菲（1988—），女，碩士研究生，主要研究方向：統計優化；黃奔茹（1992—），女，主要研究方向：統計學。E-mail：yangfeifei@mail.nwpu.edu.cn

2013-06-04

2013-07-22

1002-8331（2014）23-0036-05

CNKI網絡優先出版：2013-08-15,http://www.cnki.net/kcms/detail/11.2127.TP.20130815.1635.003.html