套代數上零點廣義Lie可導映射

費秀海，王中華

陜西師范大學 數學與信息科學學院，西安 710062

套代數上零點廣義Lie可導映射

費秀海，王中華

陜西師范大學 數學與信息科學學院，西安 710062

1 預備知識

設A是一個算子代數，L(A)表示A上的所有線性映射，f，d∈L(A)。如果對于任意的 A，B∈A，d(AB)= d(A)B+Ad(B)，則稱d是導子。如果存在 A0∈A，使得則稱d是內導子。如果對于任意的 A，B∈A，有 d([A，B])=[d(A)，B]+[A，d(B)]，則稱d是Lie-導子（其中，[A，B]=AB-BA，稱之為Lie-積）。顯然，d是內導子，則d是導子，d是導子，則d是Lie-導子，反之亦然。關于導子、內導子、Lie-導子的定義和相關結論可以在文獻[1-2]及所引用的文獻中找到。對于任意的 A，B∈A，如果存在A上一個導子d使得f(AB)=f(A)B+Bd(A)，則稱 f為廣義導子，d稱為與 f相關的導子。對于任意的 A，B∈A，如果存在S0，T0∈A，使得 f(A)=S0A-AT0，則稱 f為廣義內導子。對于任意的 A，B∈A，如果存在A上一個Lie-導子d，使得f([A，B])=f(A)B-f(B)A+Ad(B)-Bd(A)，則稱 f 為廣義Lie-導子。顯然，f是廣義內導子，則 f是廣義導子，f是廣義導子，則 f是廣義Lie-導子，反之亦然。關于廣義導子、廣義內導子、廣義Lie-導子的定義和相關結論可以在文獻[3-5]及所引用的文獻中找到。?A，B∈A且 AB=0 有 f([A，B])=[f(A)，B]+[A，f(B)]，則稱 f 是 A上零點Lie-可導映射。如果A上任意的零點Lie-可導映射都是Lie-導子，則說零點是一個Lie-全可導點。設f是代數A上的廣義Lie-導子，d為與 f相關的Lie-導子，若?A，B∈A且 AB=0有 f([A，B])=f(A)B-f(B)A+ Ad(B)-Bd(A)，則稱 f是A上廣義零點Lie-可導映射。如果A上每個廣義零點Lie-可導映射都是廣義Lie-導子，則說零點是一個廣義Lie-全可導點。關于零點Lie-可導映射、Lie-全可導點的定義和相關結論可以在文獻[6-10]及所引用的文獻中找到。

近年來，在環和各種代數上對廣義導子、廣義Lie-導子的刻畫引起了許多學者的興趣，并已取得許多重要的成果，在文獻[11]中證明了在環上的每廣義導子都可以寫成一個廣義內導子與到中心且消除交換子的可加映射的和。在文獻[12]中證明了在素環上的每個廣義Lie-導子都可以寫成一個廣義導子與到中心且消除交換子的可加映射的和。文獻[13]證明了三角代數上的廣義Lie-導子在滿足一定條件下可以寫成一個廣義導子與到中心且消除交換子的可加映射的和。關于廣義Lie-導子更多的結論可以在文獻[13]所引用的文獻中找到。本文中用到套代數A lgN相關的概念和符號如下：

設H是數域F上的一個Hilbert空間，B(H)表示H上全體有界線性算子。用I和0分別表示B(H)中的單位算子和零算子。用x?f表示H上的一秩算子（其中x∈H，f∈H*，H*是H 的對偶空間）且定義為(x?f)(y)= f(y)x，?y∈H。用 F(H)表示 B(H)中全體有限秩算子。N表示H中一個包含H和{} 0的全序的閉子空間鏈且在集合的交和閉線性張運算下封閉，把N稱為套，當時稱N為平凡套。套N相應的套代數記為A lgN，定義為：

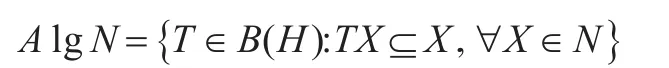
且A lgN在強算子拓撲下是閉的。顯然，當套N為平凡套時A lgN=B(H)。在本文中假定N為非平凡套。

設P1是A lgN中的一個非平凡投影且分別令：

2 定理及證明

定理2.1設 f是套代數A lgN上一個連續的零點廣義Lie-可導映射，d是與 f相關的連續Lie-導子，則f是套代數A lgN上的一個廣義Lie-導子。用以下幾個引理證明定理2.1。

引理1對于任意的冪等算子P∈A lgN，有：

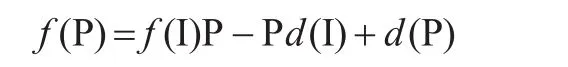
證明對于任意的冪等算子P∈A lgN，則P(I-P)=0，所以由零點廣義Lie-可導映射的定義，有：

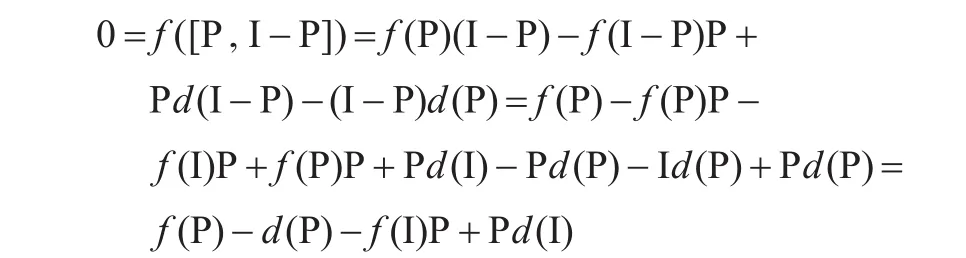
由上式，有：

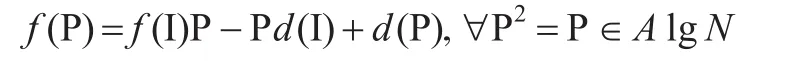
引理2對于任意有限秩算子T∈F(H)∩A lgN，有：

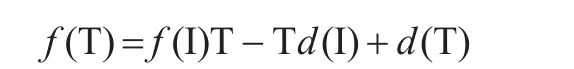
證明由參考文獻[14]知道套代數A lgN中的每個一秩算子x?f可以表示成至多4個套代數A lgN中冪等算子的線性和，不妨假設每個一秩算子xi?fi就等于4個冪等算子 Pij，j=1，2，3，4 的線性和，即

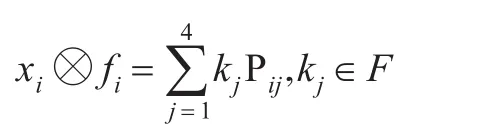
而對于套代數A lgN中的每個有限秩算子T∈F(H)∩A lgN，則可以把其表示成套代數A lgN中一秩算子的有限線性和，不妨設：

由上述兩個式子，有：

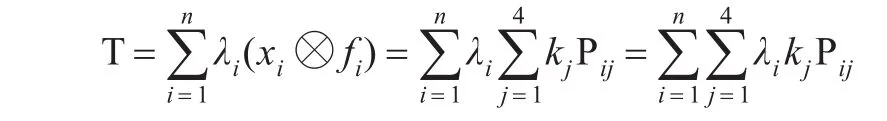
從而由引理1，有：

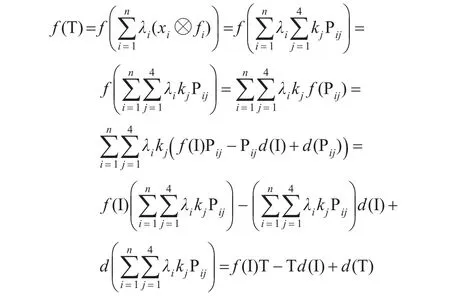
即引理2證畢。

引理3對于任意的算子A∈A lgN，有：

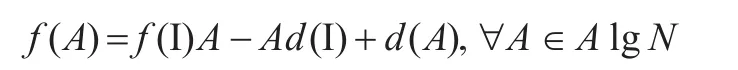
證明由參考文獻[15]知道套代數A lgN中的有限秩算子在強算子拓撲（用SOT表示強算子拓撲）下是稠密的，即

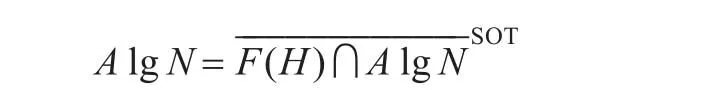
從而引理3得證。

引理4設d是零點廣義Lie-可導映射 f相關的連續Lie-導子，則有：

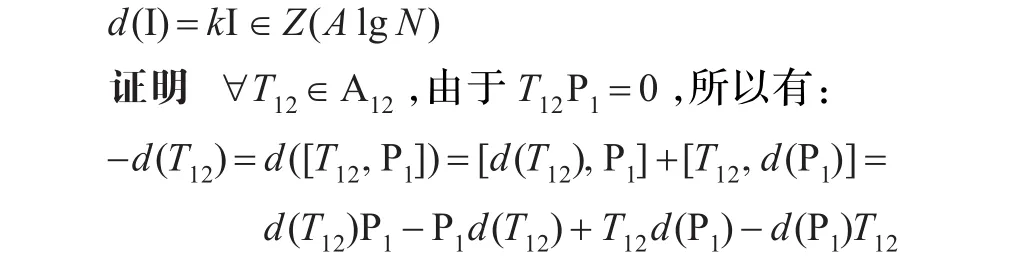
同時在上式兩邊左乘P1和右乘P2，得：

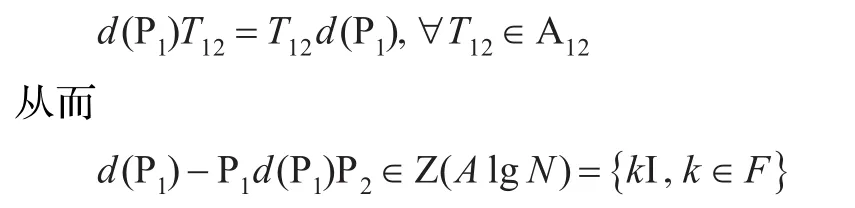
不妨設d(P1)=k1I+M12（其中k1是數域 F里面的數，M12是A12里面的算子）。

同理，因為-T12=P2T12-T12P2，所以有：

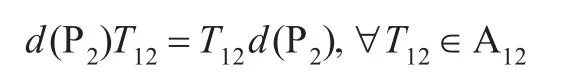
從而

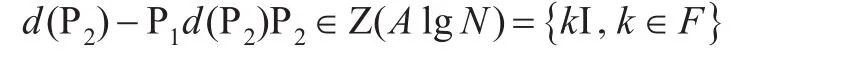
不妨設d(P2)=k2I+N12（其中k2是數域 F里面的數，N12是A12里面的算子）。

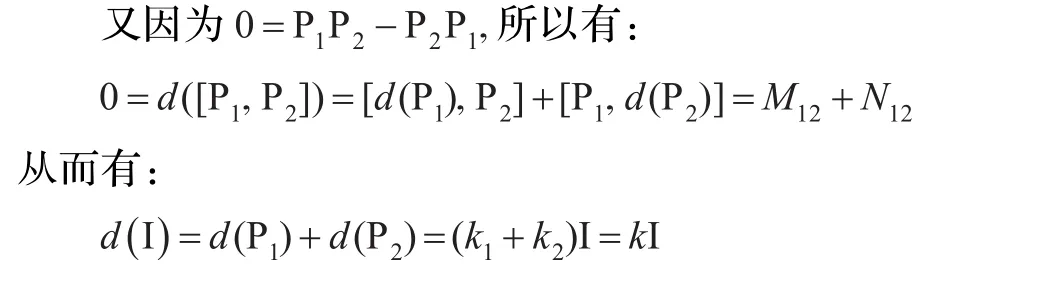
即引理4得證。

定理的2.1證明：由定理的假設及引理，?A，B∈A lgN，有：

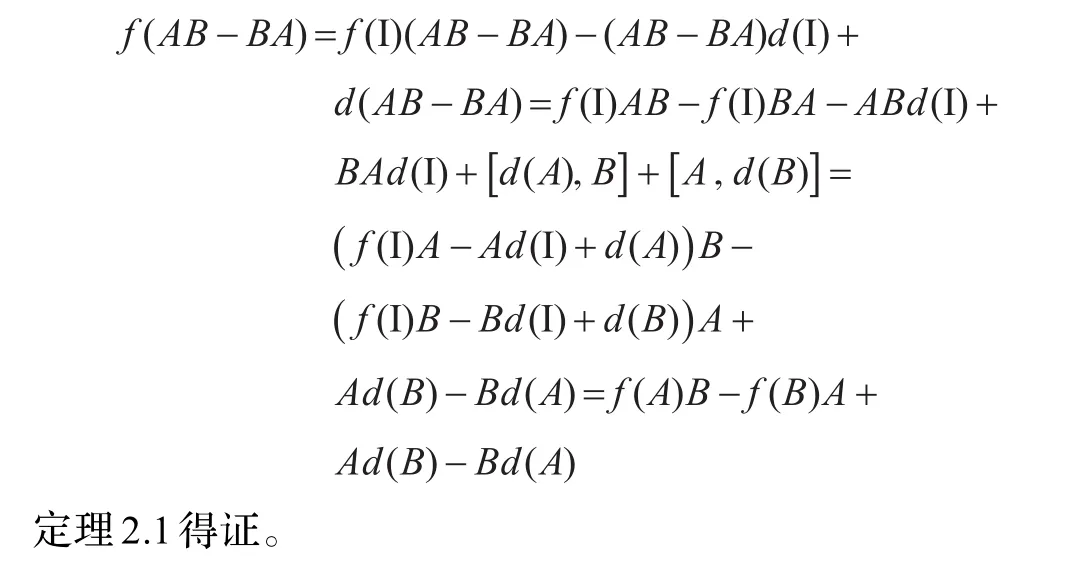
3 主要結論

本文主要對套代數A lgN上零點廣義Lie-可導映射 f作了研究，在廣義Lie-可導映射 f和相關Lie-導子d具有連續性質的假設下，證明了?A，B∈A lgN且AB=0，有：

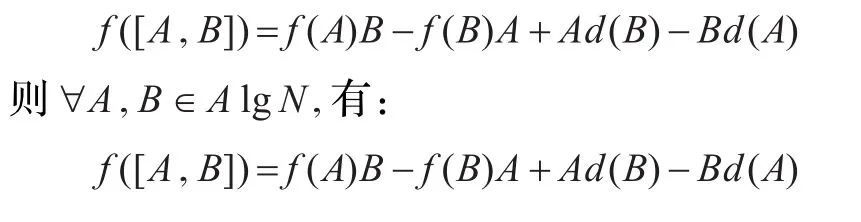
即證明了 f是套代數A lgN上的廣義Lie-導子。

[1]Christensen E.Derivations of nest algebras[J].Math Ann，1977，229：155-161.

[2]Cheung W S.Mappings on triangular algebras[D].[S.l.]：University of Victoria，2000.

[3]Nakajima A.On generalized higher derivations[J].Turk J Math，2000，24：295-311.

[4]Nakajima A.Categorical properties of generalized derivations[J].Scientiae Mathematicae，1999，2：345-352.

[5]Hou J C，Qi X F.Generalized Jordan derivations on nest algebras[J].Linear Algebra and Its Applications，2009，430：1479-1485.

[6]陳琳，張建華.套代數上的零點Lie可導映射[J].數學學報，2009（1）：107-112.

[7]Zhu Jun.Generalized derivable mappings at zero point on some reflexive operator algebras[J].Linear Algebra and Its Applications，2005，397：367-379.

[8]Zhao Jinping.Jordan higher all-derivable points on triangularalgebras[J].LinearAlgebra and ItsApplications，2012，436：3072-3086.

[9]Jing W.On Jordan all-derivable points of B（H）[J].Linear Algebra and Its Applications，2009，430：941-946.

[10]Xue Weishun.All derivable points of nest algebras on Banach space[J].Operators and Matrices，2012，6：481-491.

[11]Hvala B.Generalized derivations in rings[J].Comm Algebra，1998，26：1147-1166.

[12]Hvala B.Generalized lie derivations in prime rings[J]. Taiwanese Journal of Mathematics，2007，11：1425-1430.

[13]Benkovic D.Generalized lie derivations on triangular algebras[J].Linear Algebra and Its Applications，2011，434：1532-1544.

[14]Hadwin L B.Local multiplications on algebras spanned by idempotents[J].Linear and Multilinear Algebra，1994，37：259-263.

[15]Erdos J A.Operators of finite rank in nest algebras[J]. J London Math Soc，1968，43：391-397.

FEI Xiuhai,WANG Zhonghua

College of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710062,China

LetNbe a non-trivial nest on Hilbert spaceH，fbe a continuous generalized Lie derivable mapping at zero point on nest algebraA lgNanddbe a continuous Lie derivation on nest algebraA lgN.In this paper,It is shown that if fsatisfiesf([A，B])=f(A)B-f(B)A+Ad(B)-Bd(A)for allA，B∈A lgNwithAB=0，thenf([A，B])=f(A)B-f(B)A+ Ad(B)-Bd(A)for allA，B∈A lgN.

Lie-derivation;generalized Lie-derivation;Lie-all-derivable point;nest algebraA lgN

設N是Hilbert空間H上的一個非平凡套，f是套代數A lgN上的一個連續廣義零點Lie-可導映射，d是套代數 A lgN上的一個連續Lie-導子。證明了，如果?A，B∈A lgN且 AB=0有 f([A，B])=f(A)B-f(B)A+Ad(B)-Bd(A)，則 f([A，B])=f(A)B-f(B)A+Ad(B)-Bd(A)，?A，B∈ A lgN 。

Lie-導子；廣義Lie-導子；Lie-全可導點；套代數 A lgN

A

O177.1

10.3778/j.issn.1002-8331.1404-0414

FEI Xiuhai,WANG Zhonghua.Generalized Lie derivable mappings at zero point on nest algebras.Computer Engineering and Applications,2014,50（23）：4-6.

陜西省自然科學基礎研究計劃資助項目（No.2014JQ1015）。

費秀海（1980—），男，在讀博士，講師，研究領域為算子代數與算子理論；王中華（1984—），男，在讀博士，研究領域為算子代數與算子理論。E-mail：XiuHaiFei@snnu.edu.cn

2014-04-28

2014-06-10

1002-8331（2014）23-0004-03

CNKI網絡優先出版：2014-06-26,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1404-0414.html