EOF分析用于β中尺度暴雨系統的探索

于杰1, 2 張繼權2 張銘1

?

EOF分析用于β中尺度暴雨系統的探索

于杰張繼權張銘

1解放軍理工大學氣象海洋學院全軍危險性天氣監測預警研究中心，南京211101;2東北師范大學環境科學學院，長春130024

本文將2008年上海“8.25”暴雨過程的WRF中尺度數值模式模擬結果作為實況資料集，應用EOF（Empirical Orthogonal Function）方法對該資料集進行診斷，以探討將該方法應用于暴雨β中尺度系統的可行性。主要結論有：當數值模式輸出足夠稠密、精細的樣本，能夠較好反映實況時，利用EOF方法對天氣尺度和α、β中尺度系統的天氣過程進行診斷是可行的。對本文的暴雨過程，EOF分解位勢偏差場的前三個模態分別反映了α中尺度中端、低端和β中尺度天氣系統的演變特征，分別對應于波長和振蕩頻率不同的駐波波列。其可分別稱之為暴雨背景模態、暴雨系統模態和暴雨雨團模態。各波列物理性質不同，分別屬于準地轉的Rossby波、準平衡的渦旋波和非平衡的重力慣性波。天氣系統EOF分解的物理本質為：可將一個變形和移動的天氣系統分解為若干個具有不同物理性質且時空尺度不同相互獨立的模態（駐波波列）。這有助于明確和深化對天氣系統的認識。EOF分解能夠進行天氣系統的尺度分離，且分離后得到的各種尺度的天氣系統是獨立和有特定物理意義的，這更體現了該尺度分離方法的優點。本文中當EOF分解后各波列（模態）在某地時空指數發生三波鎖相，且該地的位勢表現為低空為負、高空為正，同時低層位勢急劇降低時，則有可能在此處發生暴雨。

EOF分析 β中尺度 暴雨 位勢高度

1 引言

EOF（Empirical Orthogonal Function）分解技術在氣候診斷中已得到充分發展，成為氣候科學研究分析變量場特征的重要工具，并取得豐碩的研究成果（Mendon?a and Bonatti，2009；Athanasiadis et al.，2010；Tao and Chen，2012；Chang et al.，2013；Xu et al.，2013；李崇銀等，2013；支星和徐海明，2013；張世軒等，2013）。然而EOF分析方法應用在天氣尺度特別是中尺度天氣系統的研究則很少，只有張銘等曾對兩個暴雨個例用EOF方法做過嘗試性的探索（安潔和張銘，2006；張銘等，2007）。分析其原因，主要是由于天氣尺度系統的常規觀測資料在時間間隔上較大，一般高空一天2次，地面一天8次；觀測站之間的距離也較大，一般在百公里以上。隨著地面自動氣象站的設立，在我國東部地區，地面觀測站間距可達10 km左右，時間間隔也縮短到一小時以內，但高空的情況卻幾乎沒有太大改變。這對于捕捉中尺度特別是β中尺度天氣信息而言，是非常不夠的。此外，天氣尺度系統的時間尺度也短，一般只有2～3天，而中尺度系統時間尺度更短，一般在一天以下甚至數小時。這樣就造成樣本資料嚴重短缺而無法使用EOF方法。隨著天氣和中尺度數值模式的發展完善，計算機性能的提高，數值模擬的效果有了很大的提升。這就使得數值模擬的結果與實際天氣之間的差異越來越小。因此將好的數值模擬結果看作實際天氣過程在時間和空間上的稠密資料集是完全可行的。又因數值模擬的輸出結果時間間隔可以很短，這樣就可獲得足夠多的樣本，從而使得應用EOF分析診斷天氣和中尺度系統成為可能。

安潔等（2006）、張銘等（2007）正是采用上述思路，將EOF用于暴雨系統的診斷分析中。上述文獻表明，EOF分析第一模態反映了暴雨天氣尺度背景場的時空演變特征，第二模態則反映了產生暴雨的α中尺度系統的時空演變特征；并指出當這兩個主分量的時間系數正相關時，激發暴雨，負相關時暴雨趨于減弱。然而該文獻所用的數值模式水平格距僅為18 km，垂直方向分21層，這樣的數值模式只能體現α中尺度系統特征，而不能細致地反映出β中尺度系統的特征。此外，這些文獻主要給出了EOF的前兩個主分量的空間結構并做了討論，而對時間系數則未做深入研究。這些都是上述文獻的不足和局限所在。

本文利用三重嵌套的WRF中尺度數值模式，對2008年8月25日上海大暴雨過程的模擬結果，應用EOF方法對該暴雨過程做了診斷分析。因該數值模式最細的空間格距為3 km，故可將該暴雨過程用EOF方法分解為若干個相互正交（獨立）的模態，分析α中尺度和β中尺度系統在該暴雨過程中的作用和影響。本文還對EOF各模態的空間結構和時間系數做了細致討論，并指出其物理本質所在。故本文不但是上述文獻的延伸和發展，也彌補了其中的不足和局限。本文也是對EOF方法應用到β中尺度特別是該尺度中、低端系統的嘗試和探索，而這正是本文的創新所在。

2008年8月25日早晨，上海市出現了強雷電和局部大暴雨天氣。該暴雨過程突發性強，降水歷時短，雨量大。06:00（北京時，下同）江蘇南部等周邊出現小到中雨，上海市僅西部郊區出現了降水云團，并產生中等降水，06:30分后上海市區降雨云團迅速發展，上海市區開始出現強降水，09:00降水明顯減小。該次降水強度很大，全市有7個自動雨量站測得降水超過了100 mm，降水時段主要集中出現在07:00～08:00。然而雨量分布卻不均，暴雨區主要出現在上海的中心城區以及其北部地區。其中，徐家匯站出現了1小時117.5 mm的超強降水，為該站自1872年有氣象記錄以來從所未遇（曹曉崗等，2009）。在該暴雨過程中還出現了具有2條螺旋臂結構的雨團（Yu and Zhang，2011）。為此，本文選用該暴雨過程作為研究個例，利用WRF模式輸出的稠密時空資料構成的充足樣本，對該次暴雨過程中的位勢偏差場做了整層的EOF診斷分析，以此來探索EOF方法應用到β中尺度系 統的可行性并揭示該暴雨過程發生、發展與EOF各模態的關系。

2 資料選取及EOF分析方法

本文利用WRF中尺度數值模式，以2008年8月24日14:00的1°×1°的NCEP再分析資料作為初始場進行數值模擬，模式積分24小時，至25日14:00；并采用三重網格嵌套方式，分辨率分別為30 km、10 km、3 km。模擬時每5分鐘輸出一次結果。將模擬結果與實際觀測數據和雷達資料做比較后發現，對大尺度、α和β中尺度天氣系統的時空分布，兩者互相一致；雨量的時空分布也趨于一致（于杰，2012）。故可認為模擬結果能夠反映實況過程，可以作為EOF分析的資料集進行研究。為 此從中選取25日02:00～14:00的細網格模式的 輸出結果，即取145個樣本，作為EOF分析的資料集。分析的空間區域為（29.5°～33.2°N，118°～122.5°E）。利用以上樣本，對模擬的位勢偏差擾動場進行EOF分解。具體做法是：首先提取位勢偏差擾動場，即由模擬各時刻輸出的位勢場減去時間平均位勢場后得到，其中，時間平均取各時刻的算術平均；然后取 850 hPa、700 hPa、500 hPa、200 hPa的偏差場作4層整體EOF分析，因為EOF分析是將一個物理量場的演變過程分解成若干個正交模態的獨立演變過程（曾慶存，1974；魏鳳英，2007），故該過程就反映了各模態對該物理量場演變的影響和貢獻。分解后得到的各模態（經驗正交函數）究竟是有物理意義的信號還是毫無意義的噪音，則應該通過顯著性檢驗。本文采用Northet al.（1982）提出的計算特征值誤差范圍的方法來進行該顯著性檢驗。若第個特征值的誤差范圍為：

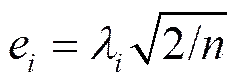
3 位勢偏差場的EOF分解結果分析

3.1 第一模態

圖1分別給出了850、700、500和200 hPa上不同層次位勢偏差場EOF第一模態空間場的分布圖。這里要說明的是，為使該圖簡潔好看，圖中等值線的數值標注為實際值的10倍，如該圖中標注的等值線2，其實際值則是2×10，而圖右邊的色標標注的則是實際值。這樣兩者看來不同，但實際上卻是一致的。圖3、圖5的情況均與圖1的情況相同，以下不再贅述。由圖1可見，850 hPa在整個研究區域內，僅在江蘇西、南部出現負值區，其中在31.2°N、119°E附近有一負值中心，而在31.2°N、121.9°E附近有正值中心（正負中心代表的是位勢高度偏差，具體偏差大小取決于時間系數），兩者位置大體與850 hPa平均場上西、東部的低壓中心重合，兩者被位勢高度偏差的0線所分割，并構成一個偶極子。該正、負中心間的距離約為300 km，上海則處于正大值中心處。700 hPa的空間場分布與850 hPa十分相似（圖1b），也有偶極子存在。500 hPa，在該區域皆為偏差正值區，其值大體由西南西向東北東方向逐漸增大；并在122°E、31.5°N附近有一個正極值中心，上海處于該正極值中心的西南部。200 hPa，則表現為整個區域都為偏差負值區，其值大體由西南向東北逐漸減小（絕對值增強），負值中心在上海的東北部海上。

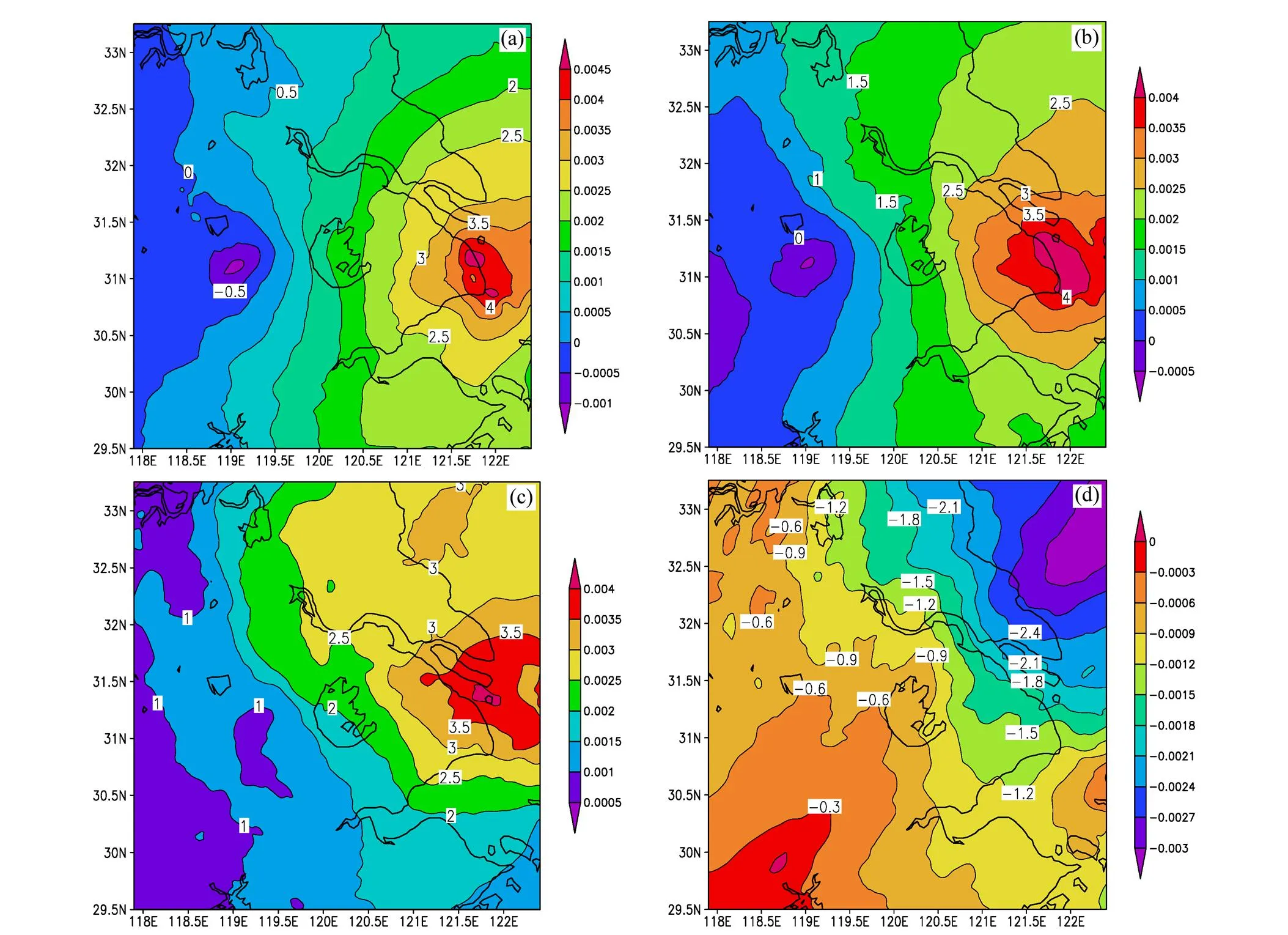
圖1 位勢偏差場的EOF第一模態（EOF1）分布：（a）850 hPa；（b）700 hPa；（c）500 hPa；（d）200 hPa。圖中等值線為實際值乘以103，色標上標注的是實際值，圖3、圖5與圖1相同

由第一模態的時間系數曲線（圖2）可見，在25日02:00～14:00的12小時中，時間系數大體呈現由正到負的半波變化形式，并且在08:20左右由正轉負，故可認為其半周期約為12小時（若有周期的話，其為24小時）。

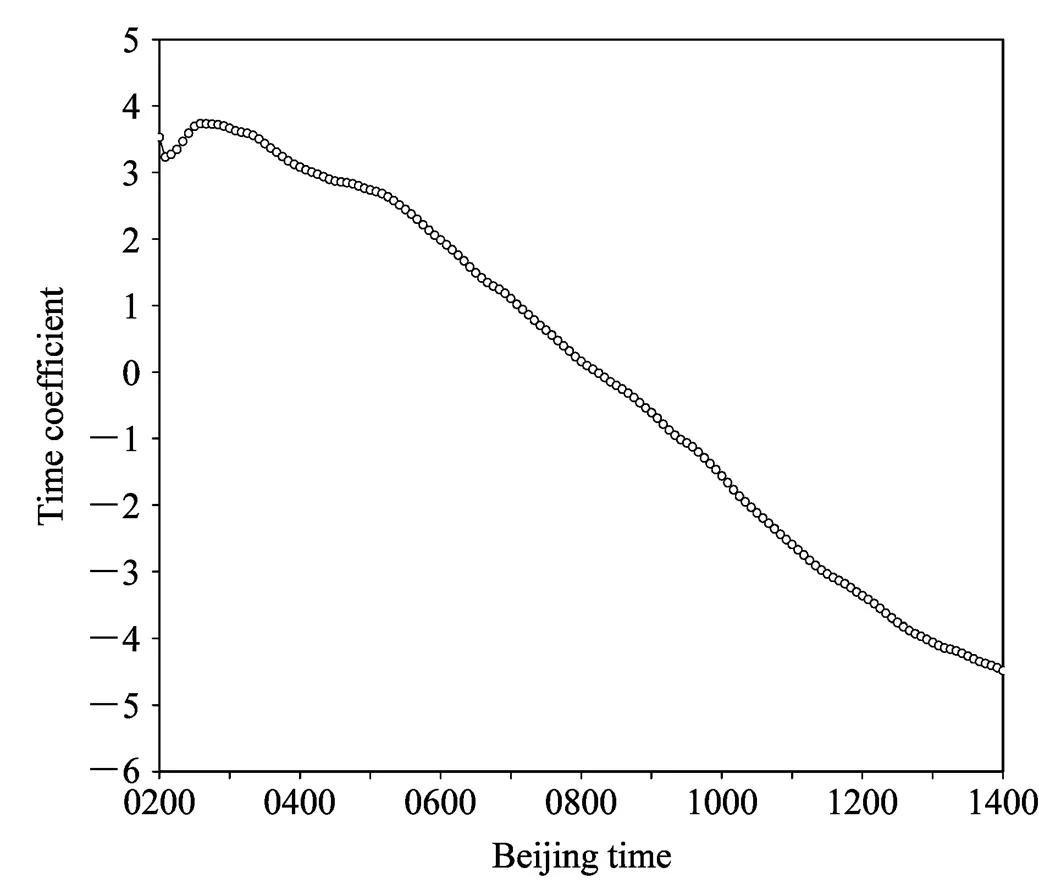
圖2 2008年8月25日位勢偏差場EOF1時間系數

綜合第一模態空間場的分布和時間系數的變化可知，在該暴雨過程中，考慮到位勢高度偏差0線的分布，可知低層有半波長約為300 km（波長約為600 km）的波列存在（偶極子可看作半個波列），其振蕩的半周期約為12小時。在該暴雨的演變過程中，位勢偏差0線以東的華東和沿海地區，低空氣壓場是持續降低的。尤其在長三角地區，降低程度最顯著，因該地區處于該偶極子正中心處。在位勢偏差0線以西地區，低空位勢場是持續升高的，其最大升高中心位于偶極子負中心處。在高空，位勢場均為升高的，其最大升高中心位于上海東北部的海上。在該暴雨的雨強最盛期，即約08:20，時間系數為0，故此時該模態位勢偏差為0，而此刻的位勢場分布即為研究時段內位勢平均場的分布。

3.2 第二模態

圖3分別給出了850、700、500和200 hPa上不同層次位勢偏差場EOF第二模態的空間場。由該圖可見，850 hPa，（31.2°N，119°E）附近和（30.8°N，122.1°E）附近各有一個正值中心，在二者之間為負值區，其中在（31.2°N，119.8°E）附近有負值中心，另在（31.3°N，121°E）附近有兩個靠得很近的強負值中心。這些正、負值中心大體構成一個波列，相鄰正、負中心距離約150 km。700 hPa空間場的分布與850 hPa十分相似（圖3b）。500 hPa，在研究區域中部為正值區，其中在（31.5°N，119.8°E）有明顯的正中心，在該正值區的西部和東部為負值區，其中在（32.2°N，118.8°E）和（31.7°N，121.5°E）附近各有一個負值中心。這些正、負中心也構成一個波列，相鄰正、負中心距離約也為150 km。200 hPa的空間場與500 hPa大體類似（圖3d），不同之處是200 hPa的負值中心較500 hPa偏向東南，而正值中心則向東北方向偏移。在研究區域第二模態空間場的主要系統總體上表現為波列的形式，其相鄰正、負中心距離約150 km，且高低層配置相反。

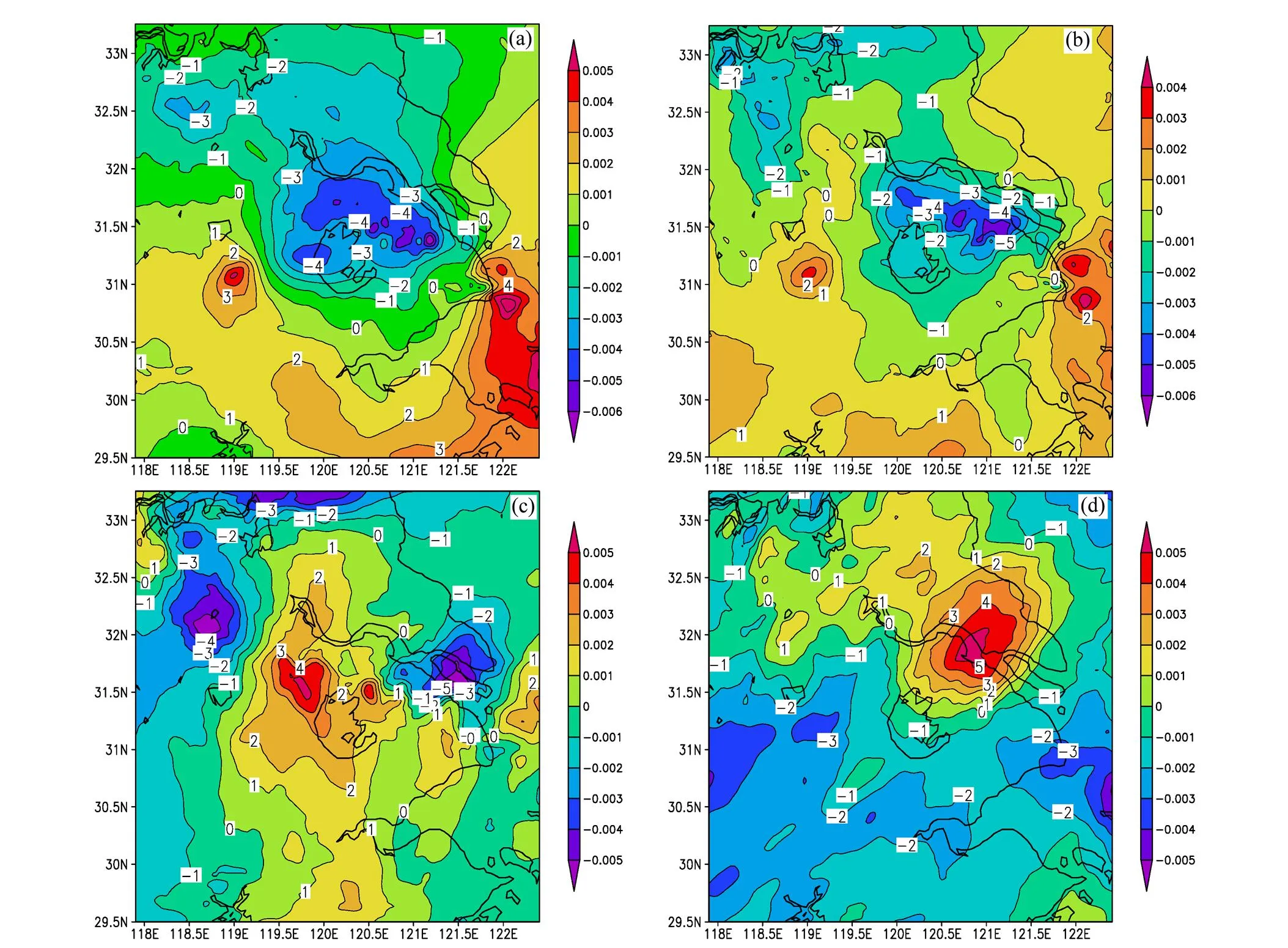
圖3 位勢偏差場的EOF第二模態（EOF2）分布：（a）850 hPa；（b）700 hPa；（c）500 hPa；（d）200hPa

由第二模態的時間系數曲線（圖4）可見，在該12小時中，時間系數呈現由負到正，再由正到負的變化，分別在25日04:50左右由負轉正，11:20左右由正轉負，即在04:50至11:20之間為正。時間系數分別在03:00左右和14:00左右達到負的最小值，08:00左右達到正的最大值。由此可見，第二模態的時間系數大體呈1波的態勢。

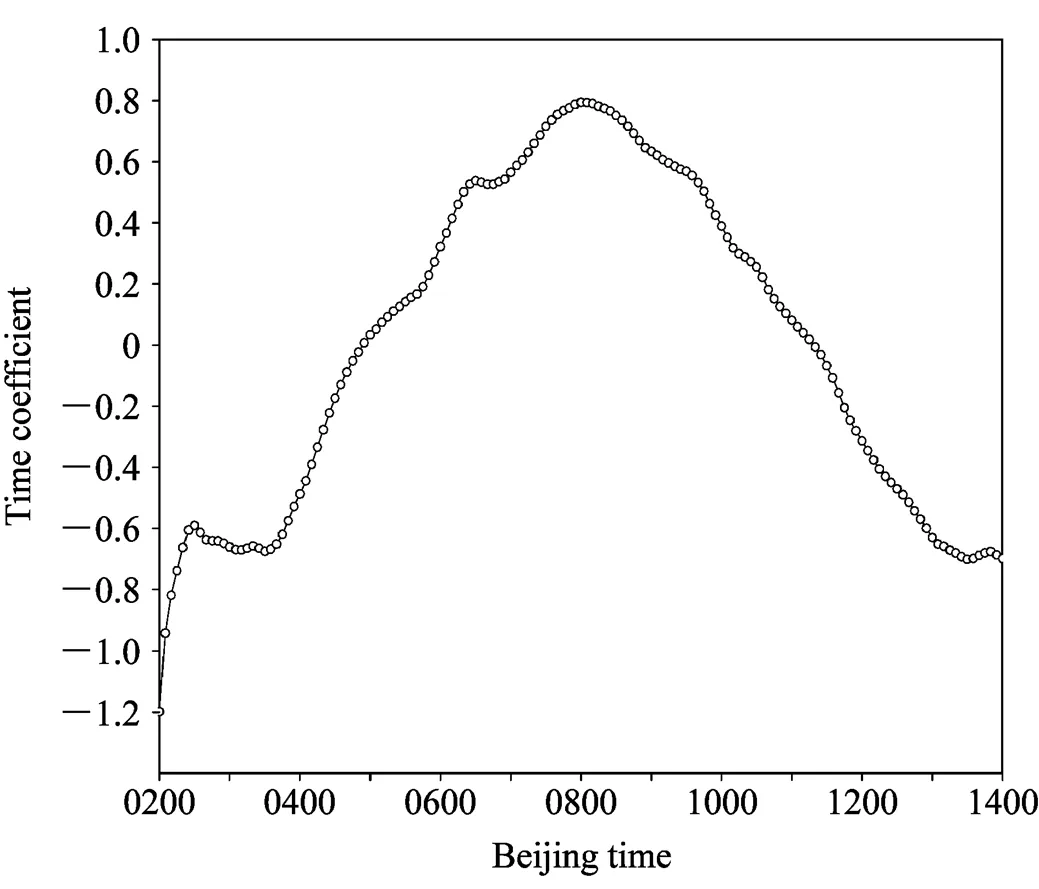
圖4 2008年8月25日位勢偏差場EOF2時間系數

綜合第二模態空間場的分布和時間系數的變化可知，在該暴雨過程中，低空有波長約為300 km的波列存在（半波長即波列相鄰正、負中心的距離約150 km），其周期約為12小時。在暴雨達到極盛前，即08:00前，長三角地區的低空位勢場是持續降低的。在暴雨達到極盛后，即08:00后，低空位勢場則持續升高。位勢場最低值出現在暴雨極盛期08:00左右。高空位勢變化則與之相反。

3.3 第三模態

圖5分別給出了850、700、500和200 hPa上不同層次位勢偏差場EOF第三模態的空間場。由該圖可見，850 hPa，長三角一帶有六個正負值中心自西向東相間排列，相鄰兩個正值（負值）中心的距離約為100 km，并組成一個波列，該波列相鄰正、負值中心間距離約為50 km。在（31°N，121.7°E）附近即上海主城區有1個負值中心，尺度約30 km，這對應于該暴雨雨團。700 hPa第三模態空間場與850 hPa大致類似，也有波列存在，在上海主城區仍然有一個同尺度的負值中心（圖5b）。500 hPa上，大體仍有正負值中心相間排列的波列，但其位置與低層有些不同。200 hPa，空間場分布與500 hPa大致類似，但配置大體相反，并也有正負中心相間排列的波列存在。總體上看，第三模態空間場的主要系統也表現為波列的形式，其波長約為100 km，且高空與中低空的配置也大體相反；中低空在上海市區的低值中心則對應于實際的上海暴雨雨團。

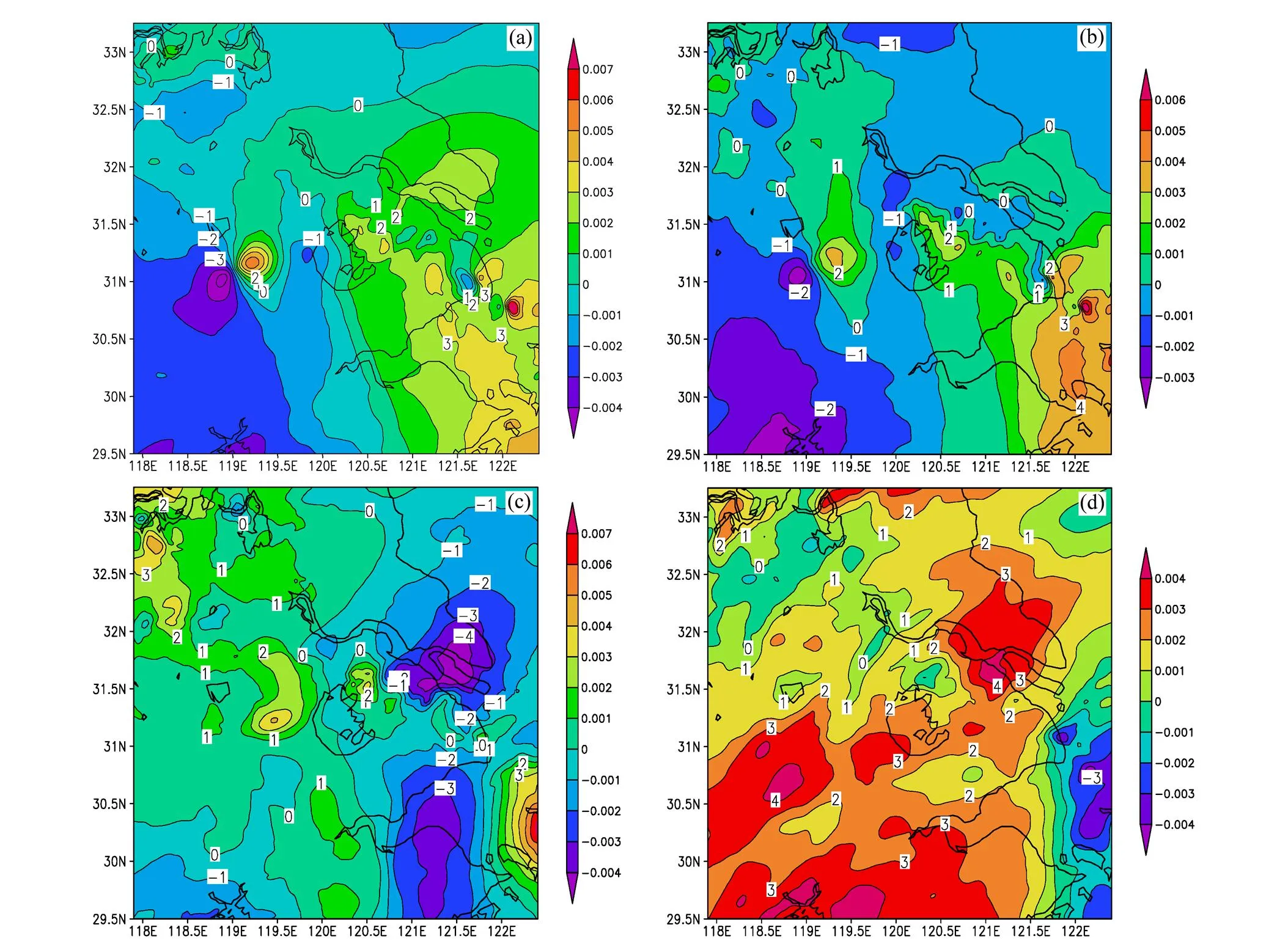
圖5 位勢偏差場的EOF第三模態（EOF3）分布：（a）850 hPa；（b）700 hPa；（c）500 hPa；（d）200 hPa

由位勢偏差場第三模態的時間系數曲線（圖6）可見，在該12小時中，時間系數分別在25日04:30左右和12:40左右達到負的最小值，07:40左右達到正的最大值。在06:20至10:40之間時間系數為正值。該時間系數呈現波動變化，且其振幅隨時間逐漸減小，其周期約為8小時。第三模態的時間系數與以上第一、二模態有所不同的是，除其周期不同外，其振幅是隨時間衰減的，而前兩個模態其振幅則隨時間變化不大；而這反映了相應于第三模態的系統（波列）其隨時間減弱的事實。

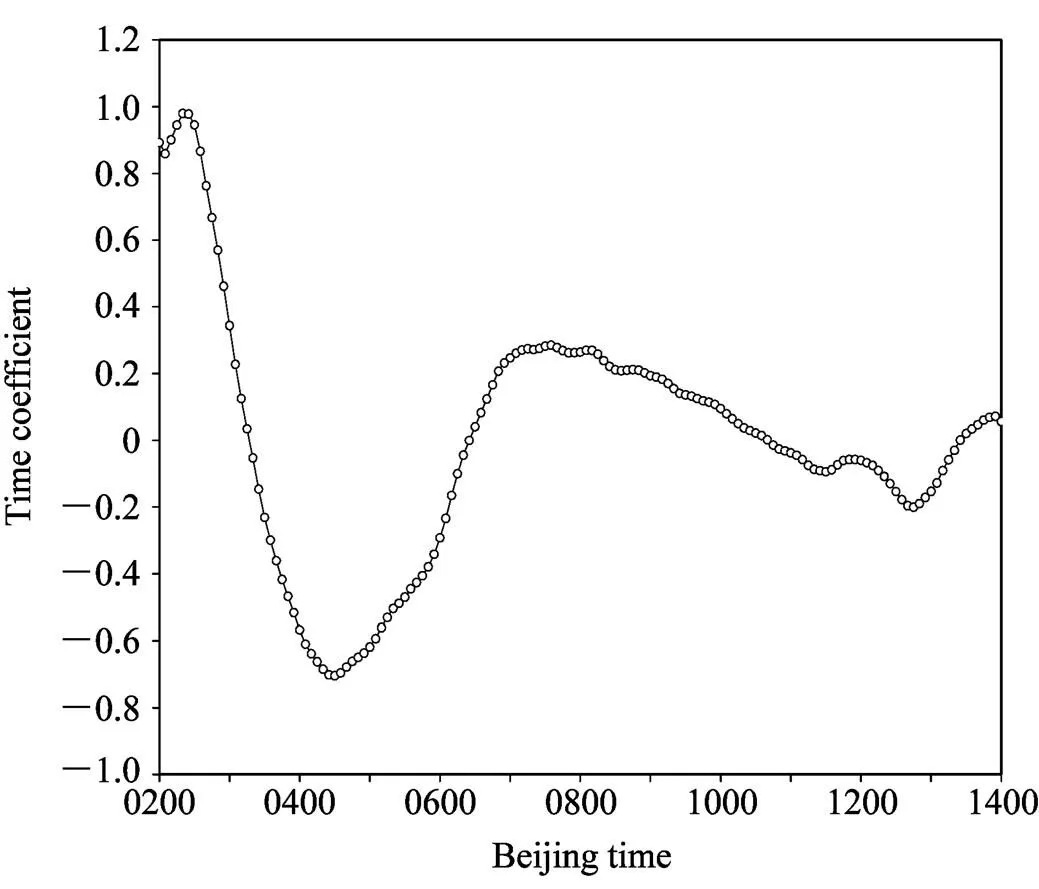
圖6 2008年8月25日位勢偏差場EOF3時間系數

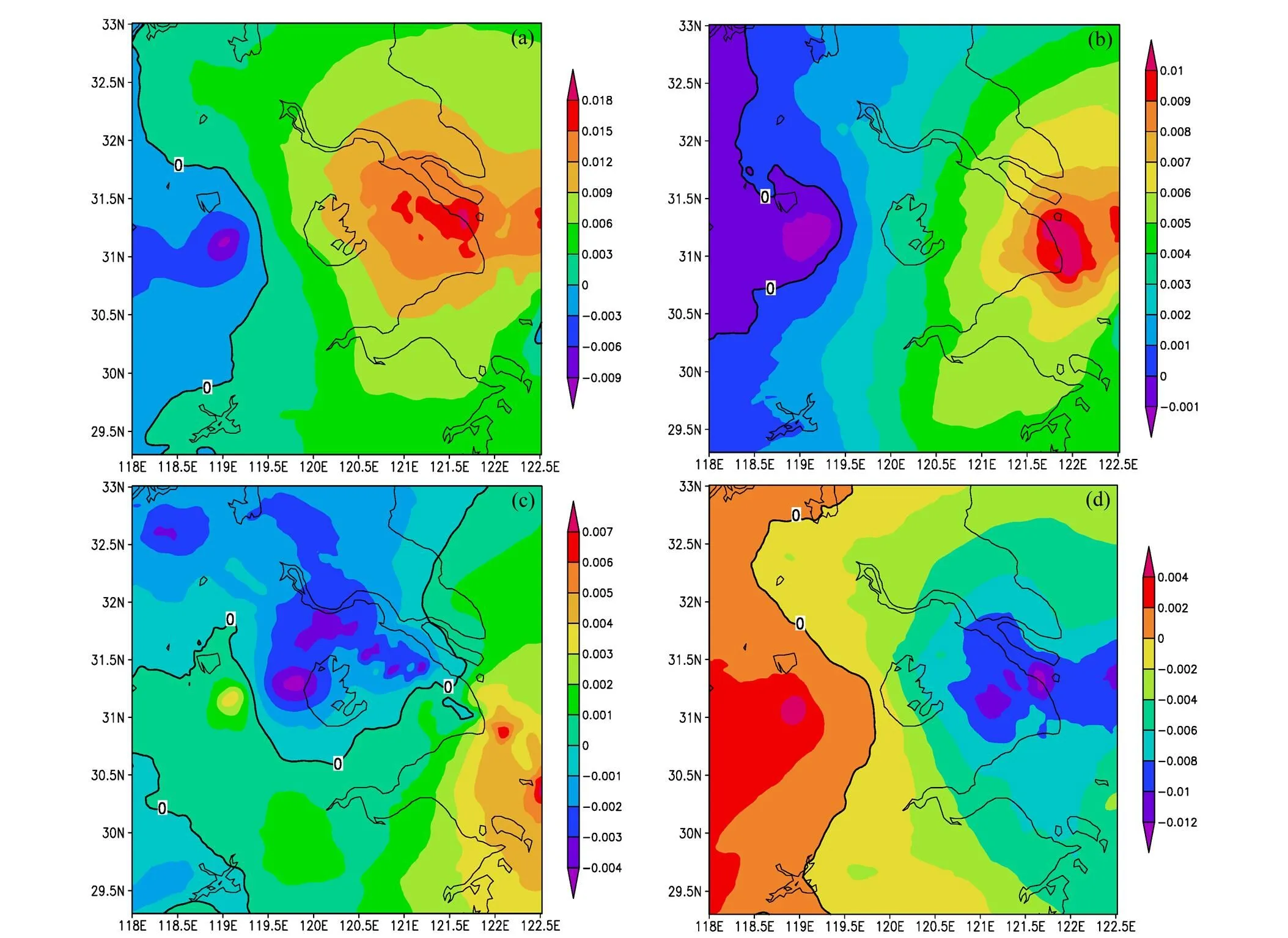
圖7 2008年8月25日850hPa位勢偏差場EOF分解前三模態疊加分布：（a）02:00；（b）05:00；（c）08:00；（d）11:00

綜合第三模態空間場的分布和時間系數的變化可知，在該暴雨過程中，低空有波長約為100 km的波列存在，其周期約為8小時。第三模態的時間系數大體呈3/2波的態勢，其振幅隨時間衰減。導致該次暴雨的系統是一個低渦形成的雨團，位勢偏差場第三模態中上海主城區的負值中心變化與該低渦的演變密切相關。該低渦初步形成于25日05:50左右，之后上海市區低空的位勢場表現為先逐漸降低，再逐漸升高的態勢；上海主城區低空位勢的最低值出現在07:40左右，以后該處的暴雨進入極盛期。由此可知，該暴雨過程與第三模態中波列的振蕩聯系緊密。

4 EOF各模態的物理性質

從以上三個模態相應的三類波列空間尺度看，因其波列波長分別為600、300、100 km（最后者含雨團尺度30 km），故其分別屬次天氣尺度（α中尺度中端）、α中尺度低端、β中尺度中端（雨團為低端）系統。設風速尺度為10 m s，中緯度地轉參數尺度為10s，則相應于這三類波列的Rossby數分別為：0.167、0.333和1.000（雨團為3.333），并分別有、和。由此可知，這三類波列大體是準地轉的，準平衡（準無輻散）的、非平衡的，且分別屬Rossby波、渦旋波、重力慣性波（含渦旋—重力慣性混合波）；它們的物理性質是完全不同的（張銘等，2008）。EOF分析中的各模態是正交的，即相互獨立的，故其物理性質的不同是很正常的。

第一模態反映了上海暴雨過程的次天氣尺度背景場特征，故可稱其為暴雨背景模態；第二模態反映了該過程中的暴雨系統演變特征，故可稱其為暴雨系統模態；第三模態則反映了該過程中的雨團演變特征，故可稱其為暴雨雨團模態。三個模態各對應于波長和振蕩頻率不同的波列。因空間場分布是固定的，這些波列在空間分布上的波形不變。而這些波列在時間上卻有駐波振蕩，這是因其時間系數隨時間有振蕩變化。故對某一模態而言，其隨時間的變化僅為駐波振蕩卻并不傳播（其空間場的0線即為該駐波振蕩的駐線）。然而，因各模態空間場的0線是相互不重合的，故該三個模態疊加后的場則隨時間會有變形和移動（圖7）。由以上可知，天氣系統EOF分解的物理本質為：可將一個變形和移動的天氣系統分解為若干個具有不同物理性質且時空尺度不同相互獨立的模態（駐波波列）。這樣就使原來較復雜的問題得以簡化。不同的模態各有自身的特點，其駐波波列波長及振蕩周期（頻率）皆不同，波列的波長越大，周期越長（頻率越低）。這也說明，EOF分解能夠進行天氣系統的尺度分離，且分離后得到的各種尺度的系統（各模態）是獨立（正交）和有特定物理意義的，這正體現了該分離方法的優點。

5 EOF模態的鎖相與暴雨

本文EOF分解得到各模態的疊加對該暴雨過程有直接的影響。因為前三個模態的方差貢獻已達93.3%，所以前三模態所代表的三類波列對該暴雨的形成發展起著決定性的影響作用。

為討論方便，本文將時間系數乘以在某處的空間模態定義為時空指數。由上海主城區位勢偏差場前三個模態的空間場可知：低空，第一模態在上海主城區處為正值，而第二、三模態為負值，高空則大致相反。在上海主城區處，低空在25日08:20，第一模態時間系數由正轉負，04:50時第二模態時間系數由負轉正，06:20第三模態的時間系數由負轉正。表1給出了上海主城區處位勢偏差場時空指數在各時間段的符號。由該表可見，約在08:20，該處三個模態的時空指數在低空和在高空符號均一致，而高、低空的符號配置卻相反；即此時分別在低空和高空，以上三類波列振蕩的位相相同；這表明此時在高、低空分別發生了時空指數的三波鎖相。而08:20正是暴雨雨團低渦形成后的降水強度極盛期。06:20在上海主城區，同上理，第二模態與第三模態的波列有兩波時空指數鎖相，而這時正是該處開始降水的時刻。這表明，雖第一模態的方差貢獻遠大于后兩個模態，但降水卻取決于后兩個模態。另外，上海主城區在04:50之前該三類波列也有三波時空指數鎖相現象。但此時時空指數低空（850和700 hPa）為正，高空（200 hPa）為負，即此時低空的位勢是升高的，而這種情況天氣不會太差。由此可知，當該三波時空指數在某地發生鎖相，且鎖相表現為低空（850和700 hPa）位勢偏差為負且高空（200 hPa）位勢偏差為正，同時低層位勢急劇降低時，則可能導致該處出現暴雨和強對流天氣（當然這還需要其他條件配合，如水汽條件和位勢不穩定等）。上海暴雨在08:20左右在徐家匯雨強達到極盛，此時正是以上三波時空指數在該處發生鎖相的結果。這也表明，EOF分析不僅能用于氣候系統，在天氣尺度和中尺度系統的統計動力診斷上，亦可發揮重要作用。

表1 上海主城區位勢偏差場時空指數隨時間變化

6 結語

本文將2008年上海“8.25”暴雨過程的WRF中尺度數值模式模擬結果看作實況資料集，應用EOF分析方法對該資料集做了統計動力診斷。所得主要結論有：

（1）當數值模式輸出足夠稠密、精細的樣本，且其能較好反映實況時，對天氣尺度和α、β中尺度系統的天氣過程，利用EOF方法進行診斷是可行的。

（2）對本文的暴雨過程，EOF分解的位勢偏差場的前三個模態分別反映了α中尺度中端、低端和β中尺度天氣系統的演變特征，且分別對應于波長和振蕩頻率不同的駐波波列。

（3）該三個模態可分別稱之為暴雨背景模態、暴雨系統模態和暴雨雨團模態，其物理性質不同，分別屬于準地轉的Rossby波、準平衡的渦旋波和非平衡的重力慣性波。

（4）天氣系統EOF分解的物理本質為：可將一個變形和移動的天氣系統分解為若干個具有不同物理性質且時空尺度不同相互獨立的模態（駐波波列），這有助于明確和深化對該系統的認識。

（5）EOF分解能夠進行天氣系統的尺度分離，且分離后得到的各種尺度的系統（各模態）是獨立（正交）和有特定物理意義的，這更體現了該尺度分離方法的優點。

（6）當本文EOF分解的各波列（模態）在某地時空指數發生三波鎖相，且該地的位勢表現為低空為負高空為正，同時低層位勢急劇降低時，此時則有可能在該處發生暴雨。

本文僅對一個暴雨個例做了EOF分析，這是不夠的。不過以上結論表明，將EOF方法應用于β中尺度系統的探索是成功的。今后將進一步在這方面用更多個例來進行深入研究。

安潔, 張銘. 2006. 中尺度暴雨過程的EOF分析 [C]. 中國氣象學會2006年年會論文集. An Jie, Zhang Ming. 2006. EOF expansion in one mesoscale rainstorm [C]. Proceeding of Chinese Meteorological Society Annual Meeting in 2006.

Athanasiadis P J, Wallace J M, Wettstein J J. 2010. Patterns of wintertime jet stream variability and their relation to the storm tracks [J]. J. Atmos. Sci., 67 (5): 1361–1381.

曹曉崗, 張吉, 王慧, 等. 2009. “080825”上海大暴雨綜合分析 [J]. 氣象, 35 (4): 51–58. Cao Xiaogang, Zhang Ji, Wang Hui, et al. 2009. Analysis on a severe convective rainstorm hitting Shanghai on 25 August 2008 [J]. Meteorological Monthly (in Chinese), 35 (4): 51–58.

Chang E K M, Zheng M H, Raeder K. 2013. Medium-range ensemble sensitivity analysis of two extreme pacific extratropical cyclones [J]. Mon. Wea. Rev., 141 (1): 211–231.

李崇銀, 李琳, 潘靜. 2013. 夏季北半球平流層環流的模態特征及變化 [J]. 科學通報, 58 (4): 365–371. Li Chongyin, Li Lin, Pan Jing. 2013. The estival modal features and transformations of stratospheric circulation in Northern Hemisphere [J]. Chinese Science Bulletin (in Chinese), 58 (4): 365–371.

Mendon?a A M, Bonatti J P. 2009. Experiments with EOF-based perturbation methods and their impact on the CPTEC/INPE ensemble prediction system [J]. Mon. Wea. Rev., 137 (4): 1438–1459.

NorthGR, Bell T L, CahalanR F, et al. 1982. Sampling errors in the estimation of empirical orthogonal function [J]. Mon. Wea. Rev., 110 (7): 699–706.

Tao L, Chen D. 2012. An evaluation of rotated EOF analysis and its application to tropical Pacific SST variability [J]. J. Climate, 25 (15): 5361–5373.

魏鳳英. 2007. 現代氣候統計診斷與預測技術 [M]. 北京: 氣象出版社, 105–147. Wei Fengying. 2007. Modern Climatic Statistical Diagnosis and Prediction Technology [M] (in Chinese). Beijing: China Meteorological Press, 105–147.

Xu Z F, Wang Y, Fan G Z. 2013. A two-stage quality control method for 2-m temperature observations using biweight means and a progressive EOF analysis [J]. Mon. Wea. Rev., 141 (2): 798–808.

于杰. 2012. 雨團與位勢穩定度的解析和數值研究 [D]. 解放軍理工大學博士論文. Yu Jie. 2012. Analytical and numerical research on rain clusters and potential stability [D]. Ph. D. dissertation (in Chinese), PLA University of Science and Technology.

Yu Jie, Zhang Ming. 2011. Analytic study on potential instability and spiral structure in rain clusters [J]. J. Trop Meteor., 17 (1): 79–86.

張銘, 安潔, 朱敏. 2007. 一次暴雨過程的EOF分析 [J]. 大氣科學, 31 (2): 321–328. Zhang Ming, An Jie, Zhu Min. 2007. EOF expansion in one rainstorm [J]. Chinese J. Atmos. Sci. (in Chinese), 31 (2): 321–328.

張銘, 張立鳳, 安潔. 2008. 大氣波譜分析及其不穩定性（第一卷），二維旋轉層結大氣中的擾動 [M]. 北京: 氣象出版社. Zhang Ming, Zhang Lifeng, An Jie. 2008. On the Wave Spectrum Analyses and Instability (I) [M] (in Chinese). Beijing: China Meteorological Press, 166.

張世軒, 封國林, 趙俊虎. 2013. 長江中下游地區暴雨“積成效應” [J]. 物理學報, 62 (6): 1–10. Zhang Shixuan, Feng Guolin, Zhao Junhu. 2013. “Cumulative effect” of torrential rain in the middle and lower reaches of the Yangtze River [J]. Acta Physica Sinica (in Chinese), 62 (6): 1–10.

支星, 徐海明. 2013. 3種再分析資料的高空溫度與中國探空溫度資料的對比: 年平均特征 [J]. 大氣科學學報, 36 (1): 77–87. Zhi Xing, Xu Haiming. 2013. Comparative analysis of free atmospheric temperature between three reanalysis datasets and radiosonde dataset in China: Annual mean characteristic [J]. Trans. Atmos. Sci. (in Chinese), 36 (1): 77–87.

曾慶存. 1974. 大氣紅外遙感原理[M]. 北京: 科學出版社,160–166. Zeng Qingcun. 1974. Principle of Atmospheric Infrared Remote Sensing (in Chinese) [M]. Beijing: Science Press, 160–166.

于杰，張繼權，張銘. 2014. EOF分析用于β中尺度暴雨系統的探索 [J]. 大氣科學, 38 (4): 795?803, doi:10.3878/j.issn.1006-9895.2013.13257. Yu Jie, Zhang Jiquan, Zhang Ming. 2014. Study on meso-β scale torrential rain with EOF [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 38 (4): 795?803.

Study on Meso-β Scale Torrential Rain with EOF

YU Jie, ZHANG Jiquan, and ZHANG Ming

1,,,211101;2,,130024

Using empirical orthogonal function (EOF) expansion, this paper analyzes the Weather Research and Forecasting (WRF) simulative data of the torrential rain occurring on August 25 of 2008 to explore the possibility of EOF expansion for diagnosing a meso-βscale torrential rain system. The conclusions show that when sufficiently fine data are consistent with real data, it is possible to diagnose mesoscale systems with EOF expansion. The preceding three modes of EOF expansion reflect the evolvement characteristics of various-scale weather systems and correspond to various wave trains with various wavelengths and oscillation frequencies: ambient mode, torrential rain system mode, and rain clusters mode. The various waves are attributed to quasi-geostrophic Rossby, quasi-equilibrium eddy, and non-equilibrium gravity inertia waves, respectively. The physical essence of EOF expansion for a weather system is that a transformative weather system with locomotion can be separated to several mutually unattached modes, or wave trains, that differ in physical characteristics, which contributes to a better understanding of the weather system. Scale separation for weather systems is an advantage of EOF expansion because separate weather systems are unattached and have particular physical characteristics. When the space–time indices of different wave trains are in phase lock, a strongly convective precipitation will occur in the appropriate weather condition.

EOF expansion, Meso-β scale, Torrential rain, Geopotential height

1006–9895(2014)04–0795–09

P443

A

10.3878/j.issn.1006-9895.2013.13257

2013?09?04，2013?10?28收修定稿

“十二五”農村領域國家科技支撐計劃課題2011BAD32B00-04，國家自然科學基金項目41371495，國家自然科學青年基金項目41005030

于杰，女，1974年出生，博士，主要從事中尺度氣象學的研究。E-mail: yujieair@126.com