亞正定矩陣的充要條件

黃 毅

（1.成都大學(xué) 信息科學(xué)與技術(shù)學(xué)院，四川 成都 610106；2.模式識別與智能信息處理四川省高校重點實驗室，四川 成都 610106）

0 引 言

對于矩陣正定性的研究，過去一直局限于實對稱矩陣 和Hermite矩 陣.例 如，1970年，Johnson［1］引入了不再局限于實對稱矩陣和Hermite矩陣的實正定矩陣的概念；1985年，Horn等［2］給出了實正定矩陣的定義，而李炯生［3］對廣義正定矩陣的性質(zhì)和特征做了較深入的研究；其后，屠伯塤提出了亞正定矩陣的概念，并對其做了較系統(tǒng)的論證與研究，認(rèn)為實正定矩陣實際上就是亞正定矩陣，這2個概念是等價的，它們都是把實對稱矩陣的限制去掉了［4－5］.本研究使用亞正定矩陣的概念，建立了亞正定矩陣的一些充分和必要條件.

1 定 義

先說明一些本研究使用符號：R 表示實數(shù)集；C表示復(fù)數(shù)集；Mn（P）表示數(shù)域P上n階方陣的集合；Rn×1表示全體n維實列向量集合；Cn×1表示全體n維復(fù)列向量集合；AT表示矩陣A 的轉(zhuǎn)置；ˉA 表示矩陣A 的復(fù)共軛；A＊表示矩陣A 的共軛轉(zhuǎn)置，即A＊＝ˉAT.

定義1（實對稱矩陣，實反對稱矩陣，Hermite矩陣和反Hermite矩陣） 如果A ＝AT，矩陣A ∈Mn（R）稱為實對稱矩陣；如果A ＝－AT，矩陣A ∈Mn（R）稱為實反對稱矩陣；如果A ＝A＊，矩陣A ∈Mn（C）稱為Hermite矩陣；如果A ＝－A＊，矩陣A∈Mn（C），稱為反Hermite矩陣.

定義2（實對稱正定矩陣） n 階實對稱矩陣A稱為實對稱正定矩陣，如果對于任一非零實向量，X∈Rn×1，都有XTAX ＞0.

定義3（實方陣的對稱分支和反對稱分支） 事實上，實方陣可唯一地表示成，

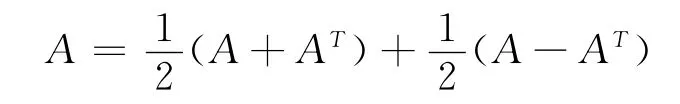
的分解形式.令，

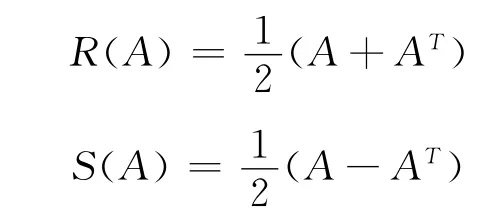
則，

A ＝R（A）＋S（A）.

其中，R（A）是實對稱矩陣，稱為實方陣A 的對稱分支；S（A）是實反對稱矩陣，稱為實方陣A 的反對稱分支.以下的分解式，A ＝R（A）＋S（A），均指這種意義的分解.

定義4（實正定矩陣） 設(shè)A ∈Mn（R），如果對于任一非零實向量，X ∈Rn×1，都有，XTAX ＞0，則稱A 為實正定矩陣［1－3］.

定義5（亞正定矩陣） 如果實方陣A的對稱分支R（A）是實對稱正定矩陣，則稱A 為亞正定矩陣［4］.

實正定矩陣和亞正定矩陣這2 個概念是等價的［4］，本研究使用亞正定矩陣的概念.“亞”字在漢語里有“次一等”的意思.顧名思義，亞正定矩陣就是滿足的條件少于普通的實對稱正定矩陣的正定矩陣.

定義6（主子陣和順序主子序） 一個方陣中相同的行標(biāo)和列標(biāo)的行和列的交叉元素所形成的矩陣稱為這個方陣的主子陣.一個方陣A 的k階主子陣，

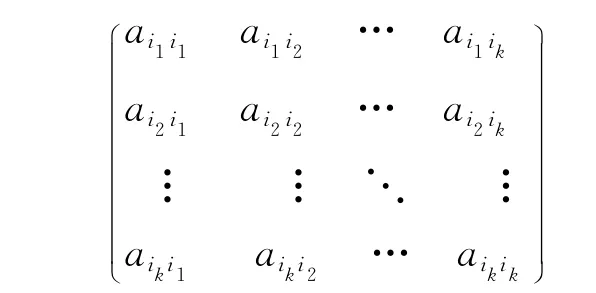
其中，1 ≤i1＜i2＜… ＜ik≤n，可用符號來表示.特別地，主子陣稱為A 的k 階順序主子陣.

2 亞正定矩陣的充要條件

定理1 設(shè)A ∈Mn（R），則A 是亞正定矩陣的充分必要條件是，存在P ∈Mn（C）非奇異，使得，

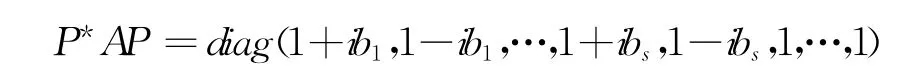
證明

1）必要性.A 是亞正定矩陣?R（A）實對稱正定?存在Q ∈Mn（R）非奇異，使得，

其中，In為n 階單位矩陣.

因為，QTS（A）Q ∈Mn（R），所以，

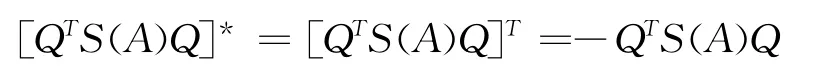
故，QTS（A）Q 是反Hermite矩陣.由于實矩陣QTS（A）Q 的虛特征值共軛成對出現(xiàn)，且反Hermite矩陣的特征值為零或純虛數(shù)，故QTS（A）Q 的特征值可以表示為，ib1，－ib1，…，ibs，－ibs，0，…，0，其中，bm＞0，m ＝1，2，…，s.

又，反Hermite矩陣QTS（A）Q 是正規(guī)矩陣?存在酉矩陣U 使得，

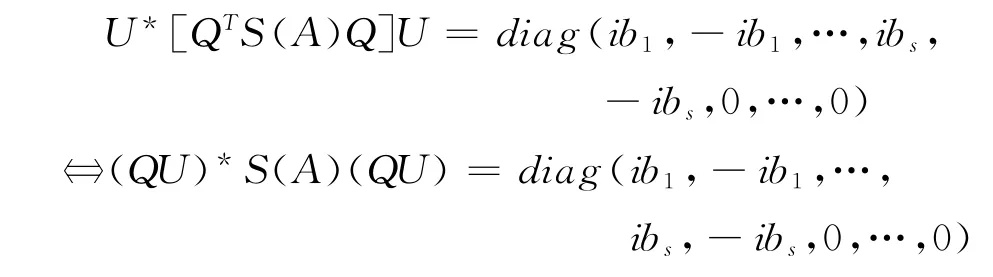
令，QU ＝P ∈Mn（C），則P 是非奇異矩陣，有，

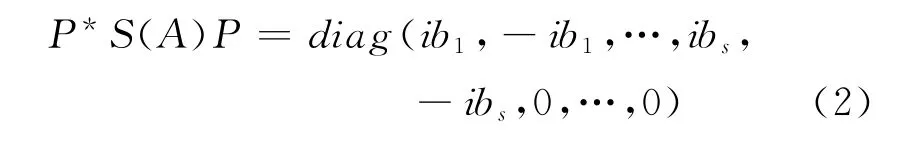
式（1）兩端各自左乘U＊右乘U 得，

其中，In是n 階單位矩陣.

式（2）＋式（3）得，

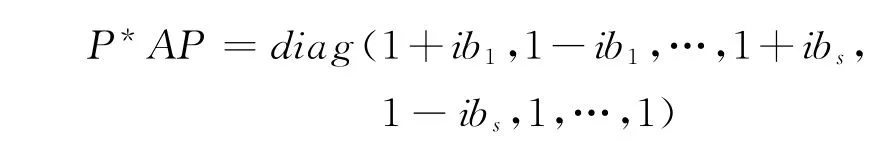
因為P＊和P 皆非奇異，一個矩陣乘上非奇異陣不改變秩，所以由式（2）得，

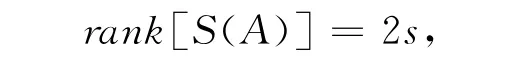
即，

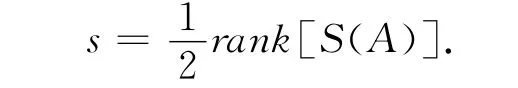
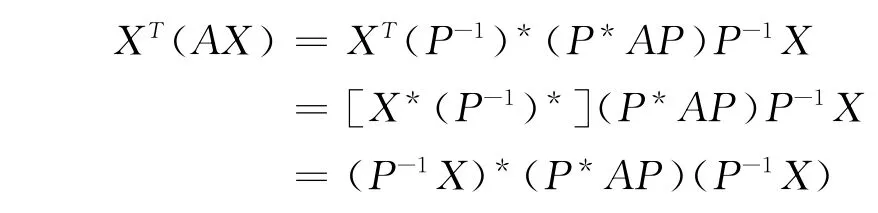
令，P－1X ＝Y(jié) ≠0，有，

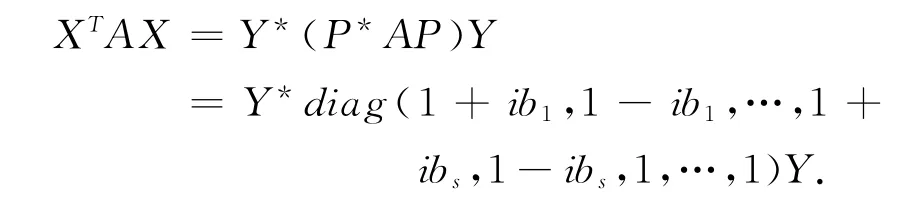
再令，Y ＝（y1，y2，…，yn）T，其中，yi∈C，且yi不全為零，i＝1，2，…，n，則，

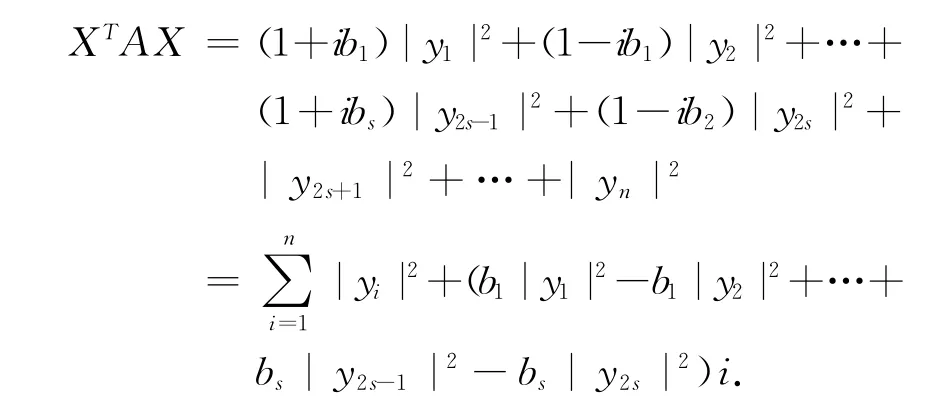
因，XTAX ∈R，由上式兩端比較可得出，

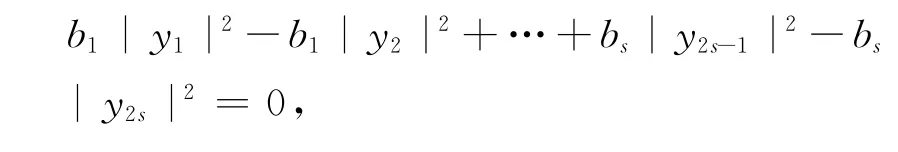
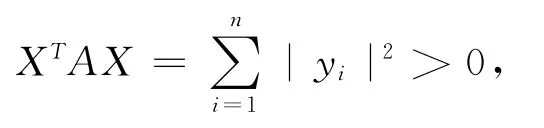
因此，A 是亞正定矩陣，

定理2 設(shè)A ∈Mn（R），則A 是亞正定矩陣的充分必要條件是，存在P ∈Mn（C）非奇異，使得，

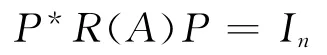
其中，In是n 階單位矩陣.

證明

1）必要性.由定理1必要性的證明過程知式（3）成立.

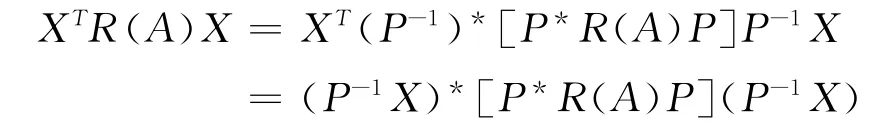
令，P－1X ＝Y(jié) ≠0，有，

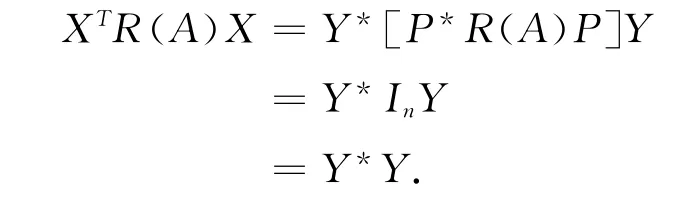
再令，Y ＝（y1，y2，…，yn）T，其中，yi∈C，且yi不全為零，i＝1，2，…，n，則，

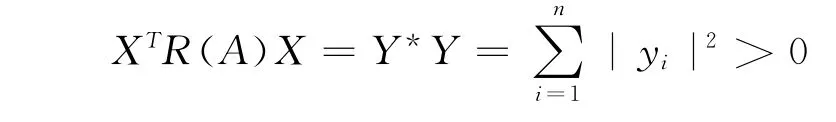
所以，A 是亞正定矩陣.

定理3 設(shè)A ∈Mn（R），則A 是亞正定矩陣的充分必要條件是，存在P ∈Mn（C）非奇異，使得，

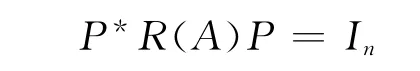
其中，In是n 階單位矩陣，

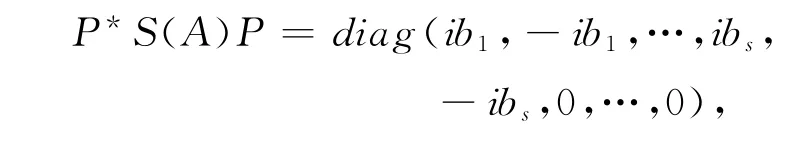
證明

1）必要性.由定理1 必要性的證明過程知式（2）、（3）成立.

2）充分性.由定理2知成立.

定理4 設(shè)A ∈Mn（R），則A 是亞正定矩陣的充分必要條件是，對任意實數(shù)t∈［0，1］，tA ＋（1－t）B 是亞正定矩陣，其中，B ∈Mn（R）是亞正定矩陣.

證明

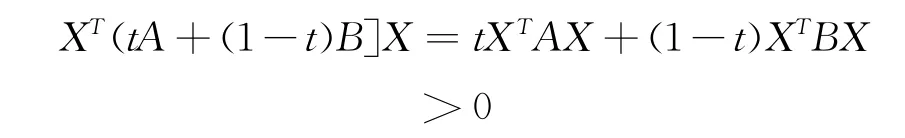
故，tA ＋（1－t）B 是亞正定矩陣.

這一結(jié)論說明，n階亞正定矩陣集合為一凸集.

2）充分性.令t＝1即得.

需說明的是，如果定理4中的條件t∈［0，1］改為t∈（0，1），就不能推出A 是亞正定矩陣.例如，設(shè)B 是亞正定矩陣，A ＝0，則t∈（0，1），有tA ＋（1－t）B＝（1－t）B是亞正定矩陣，但A ＝0不是亞正定矩陣.

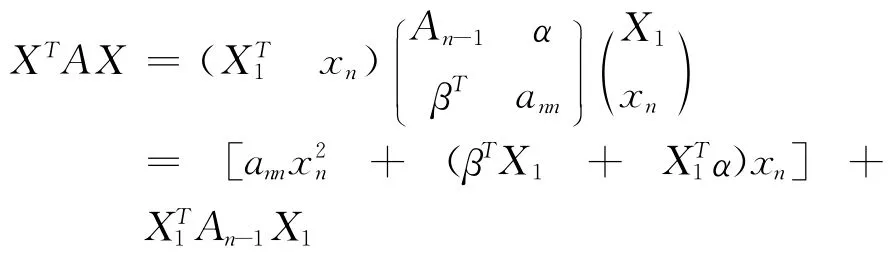
當(dāng)ann≠0時，

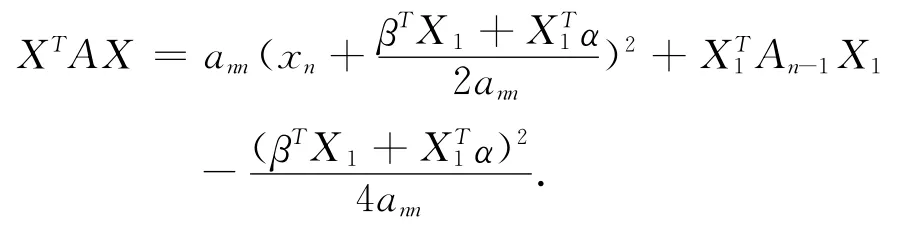
因 為，βTX1和XT1α都是數(shù)，所以βTX1＝，故，

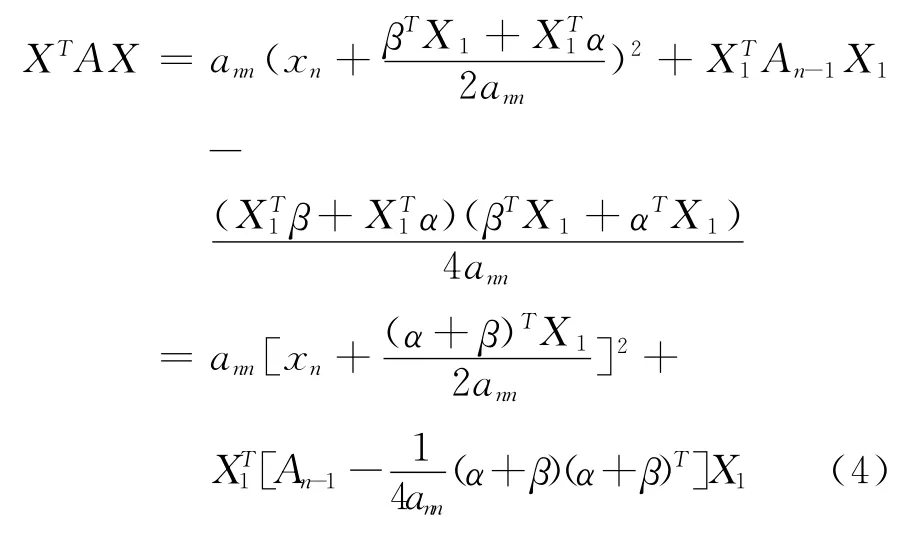
1）充分性.因ann＞0，且β）T是亞正定矩陣，故，當(dāng)X1≠0時，由式（4）得，XTAX ＞0.當(dāng)X1＝0時，必有xn≠0，由式（4）亦得XTAX ＞0.故A 是亞正定矩陣.

2）必要性.因為A 是亞正定矩陣，其主對角元素全 為 正 實 數(shù)［6］，故ann＞0，X1≠0，X1∈

R（n－1）×1，取，

由式（4）有，

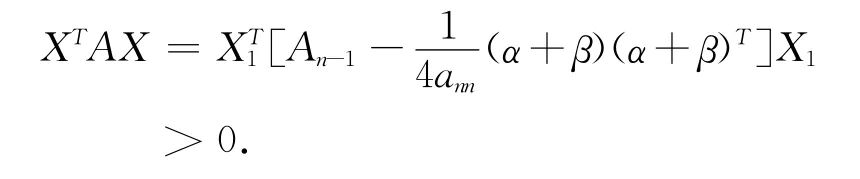
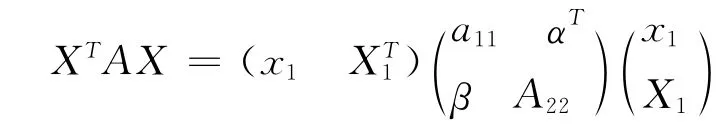
當(dāng)a11≠0時，

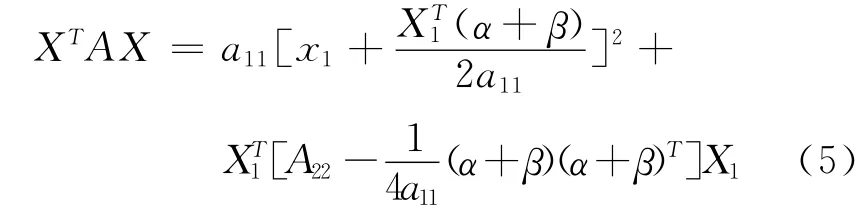
1）充分性.因a11＞0，且β）T是亞正定矩陣，故，當(dāng)X1≠0時，由式（5）得，XTAX ＞0.當(dāng)X1＝0時，必有x1≠0，由式（5）亦得XTAX ＞0.故A 是亞正定矩陣.

2）必要性.因為A 是亞正定矩陣，故a11＞0，X1≠0，X1∈R（n－1）×1，取，

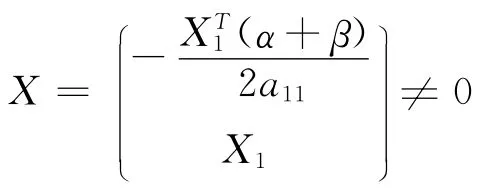
由式（5）有，

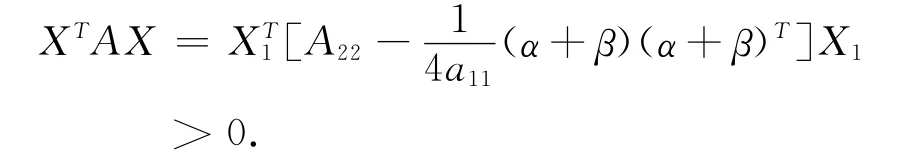
注意，定理5和定理6的2個充要條件給出了亞正定矩陣的2個降階判別法.

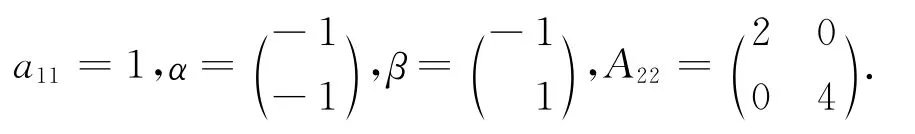
因為，a11＞0，

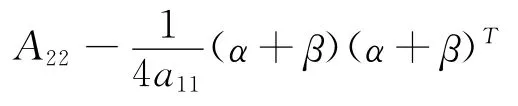
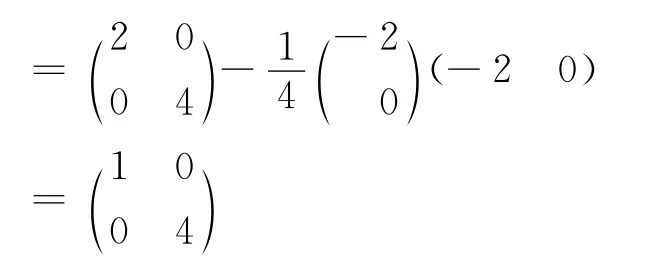
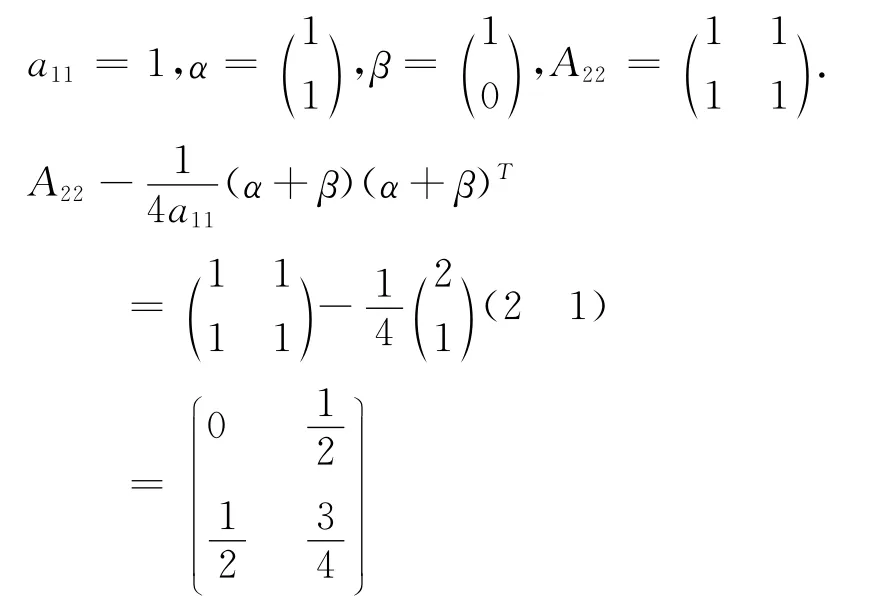
［1］Johnson C R.Positive definite matrices［J］.The American Mathematical Monthly，1970，77（3）：259－264.

［2］Horn R A，Johnson C R.Matrix analysis［M］.Cambridge：Cambridge University Press，1985.

［3］李炯生.實方陣的正定性［J］.數(shù)學(xué)的實踐與認(rèn)識，1985，15（3）：67－73.

［4］屠伯塤.亞正定陣?yán)碚摚↖）［J］.數(shù)學(xué)學(xué)報，1990，33（4）：462－471.

［5］屠伯塤.亞正定陣?yán)碚摚↖I）［J］.數(shù)學(xué)學(xué)報，1991，34（1）：91－94.

［6］黃毅，歐鵬.亞正定矩陣的基本性質(zhì)［J］.成都大學(xué)學(xué)報（自然科學(xué)版），2014，33（1）：20－22.