基于收縮估計法的廣義Pareto分布參數的估計*
陳兆仁,劉婉貞
基于收縮估計法的廣義Pareto分布參數的估計*
陳兆仁1,劉婉貞2
(1.湖南師范大學工程與設計學院,湖南長沙410081;2.長沙職業技術學院,湖南長沙410010)
由于廣義Pareto分布在金融和保險等領域的廣泛應用,對于該分布的統計推斷成為研究的熱點.將在參數的先驗分布為倒伽瑪分布條件下研究廣義Pareto分布參數的Bayes估計問題,并在平方誤差和LINEX損失函數下,導出了參數的Bayes估計和Bayes收縮估計.文末給出了Monte Carlo數值模擬試驗和結論.
廣義Pareto分布;Bayes估計;收縮估計;損失函數
廣義Pareto分布(GPD)自Piekands[1]提出以來被廣泛地應用于金融、保險、災害預測等諸多領域.關于其統計推斷研究引起了很多學者的關注.Rasmussen[2]提出了GPD參數估計的廣義概率加權法;趙旭等[3]針對截尾樣本提出了GPD參數估計的廣義有偏概率加權矩法;Ashkar等[4]對以前學者提出的最大似然估計法、矩估計法、概率加權矩估計法以及廣義概率加權矩估計法進行回顧總結,發現這些方法在形狀參數為正值時,廣義Pareto分布參數常有一個上界值.特別是在處理洪水數據時,這種情況常出現,以往的方法得到的估計值常高出這個上限值,于是其利用Monte Carlo數值模擬對幾類估計方法進行比較,進而提出了一些建議.在工程實踐中,很多學者意識到將有關未知參數的先驗知識融入到參數的估計中將能改善原有的估計,如收縮估計.Thompson[5]提出了估計總體均值參數的如下收縮估計:
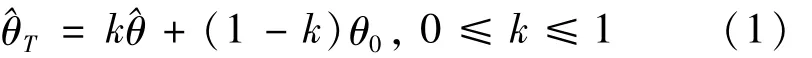
這里θ0為參數先驗值,^θT稱為Thompson型估計.關于收縮估計的更多的研究參見文獻[6-8].基于收縮技術研究GPD參數估計問題還未見有文獻討論,因此本文討論GPD參數的Bayes收縮估計問題.由于在實際中用的最多的是兩參數GPD分布:
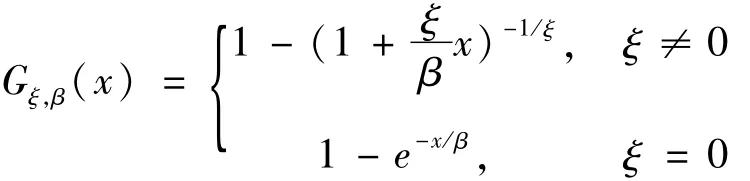
其中β>0.且當ξ≥0時,x∈[0,∞);當ξ<0時,x∈[0,-].于是本文接下來的研究中只考慮參數ξ<0的情況.令θ=-ξ,σ=,則此時兩參數GPD分布變為:
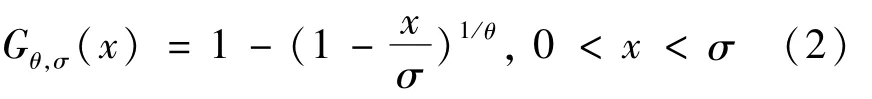
其中θ,σ>0為參數.
本文將在σ已知的情況下,在參數θ的先驗分布為倒伽瑪分布的條件下,研究在平方誤差損失、LINEX損失函數下廣義Pareto分布參數的Bayes收縮估計問題.
1 預備知識
引理1 設X1,X2,…,Xn為來自廣義Pareto分布(2)的簡單隨機樣本,記X=(X1,X2,…,Xn),t的樣本觀測值,設參數θ的先驗分布為逆伽瑪分布IΓ(α,β),相應的概率密度函數為:
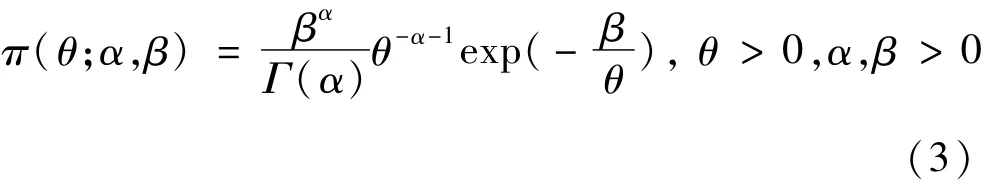
(iii)θ|X~IΓ(n+α,β+T).
證由(1)得到,在給定x=(x1,x2,…,xn)下,參數θ的似然函數為:
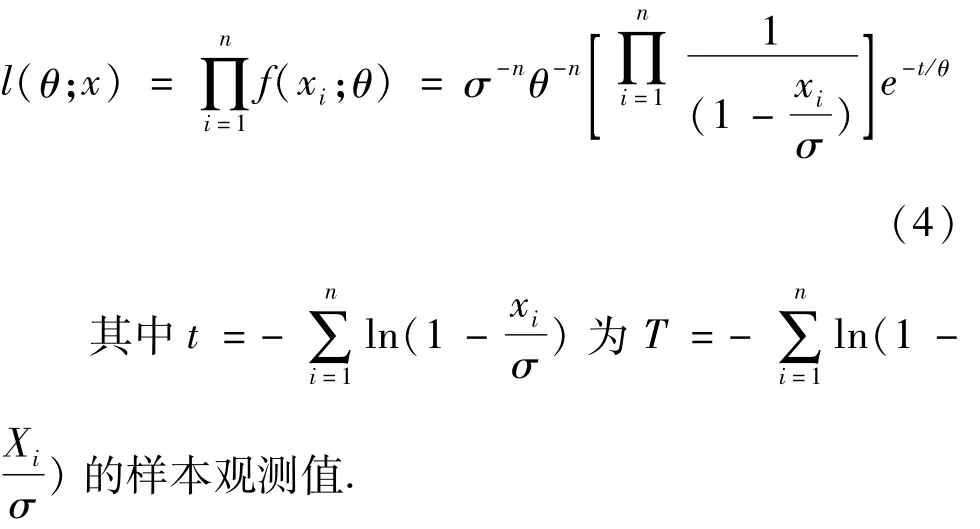
由(3)、(4)及Bayes定理,參數θ的后驗概率密度函數為:
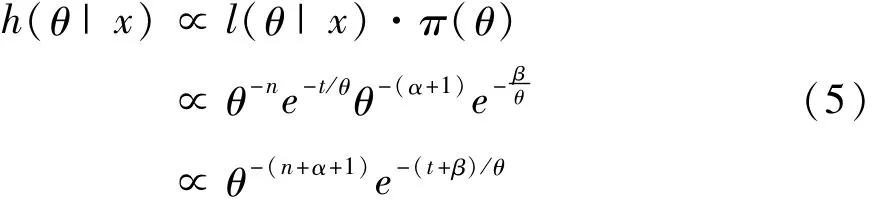
從而θ的后驗分布為倒伽瑪分布IΓ(n+α,t+β).即后驗概率密度函數為:
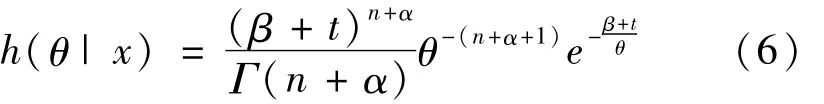
引理得證.
2 Bayes估計和Bayes收縮估計
在這一部分,我們總設X=(X1,X2,…,Xn)為來自分布(2)的容量為n的簡單隨機樣本,并設T為研究參數的Bayes估計問題,下面將在平方誤差損失函數和LINEX損失函數下研究參數的Bayes和Bayes收縮估計問題.
2.1平方誤差損失函數下的Bayes估計和Bayes收縮估計
在平方誤差損失函數L1(^θ,θ)=(^θ-θ)2下,參數θ的Bayes估計為其后驗期望,即有:
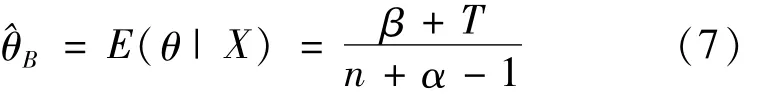
現假設根據已有的工程經驗已知參數θ的先驗估計值為θ0,采用文獻[8]的方法確定超參數α,β值:令E(^θB)=θ0,由引理1得β=(α-1)θ0,將其代入(7)有:
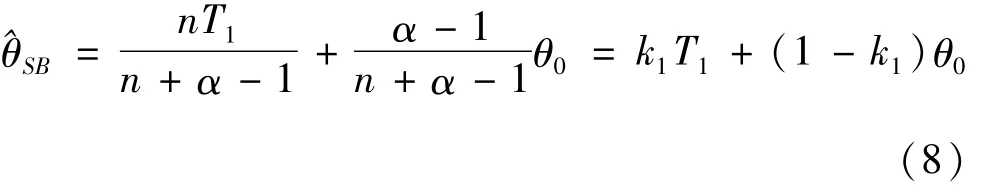
這恰好具有(1)的形式,我們把通過這種方法得到的估計稱為Bayes收縮估計.
2.2LINEX損失函數下的Bayes估計和Bayes收縮估計
本文采用的LINEX損失函數是由文獻[9]首先提出的,其函數表示形式為:
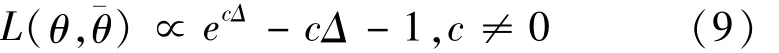
易證在LINEX損失函數下參數θ的Bayes估計由下式給出:
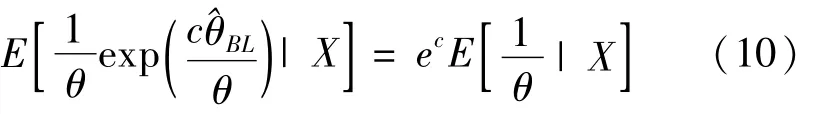
由于
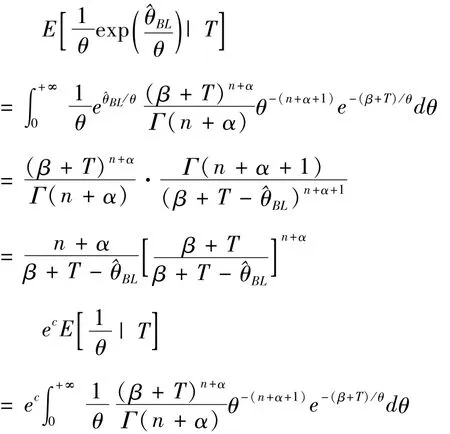
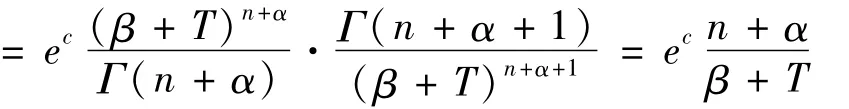
則由(9)解得在LINEX損失函數下,參數θ的Bayes估計為:
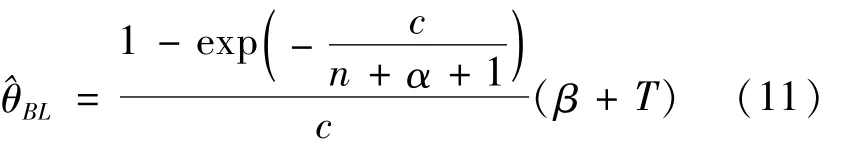
下面采用類似的方法確定先驗分布中的超參數α,β值:
令E(^θBL)=θ0,由引理1得

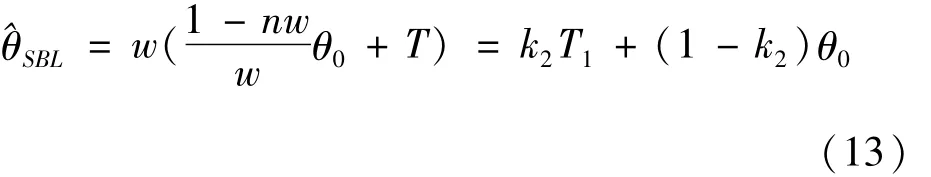
將β值(12)代入(11)中,有:這里k2=nw.這也具有(1)的形式,也稱為Bayes收縮估計.
3 數值模擬例子
利用Monte Carlo數值模擬生成容量為n=20的來自廣義Pareto分布(2)的簡單隨機樣本,其中σ=1.0,θ=1.0.重復試驗N=5000次,將估計的平均值即作為參數θ的估計值,利用均方誤差
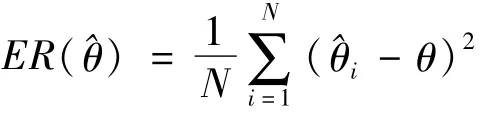
來考察估計的優良性,其中^θi為第i次試驗的參數θ的估計值.參數的最大似然估計(MLE)、Bayes估計以及Bayes收縮估計值見表1.
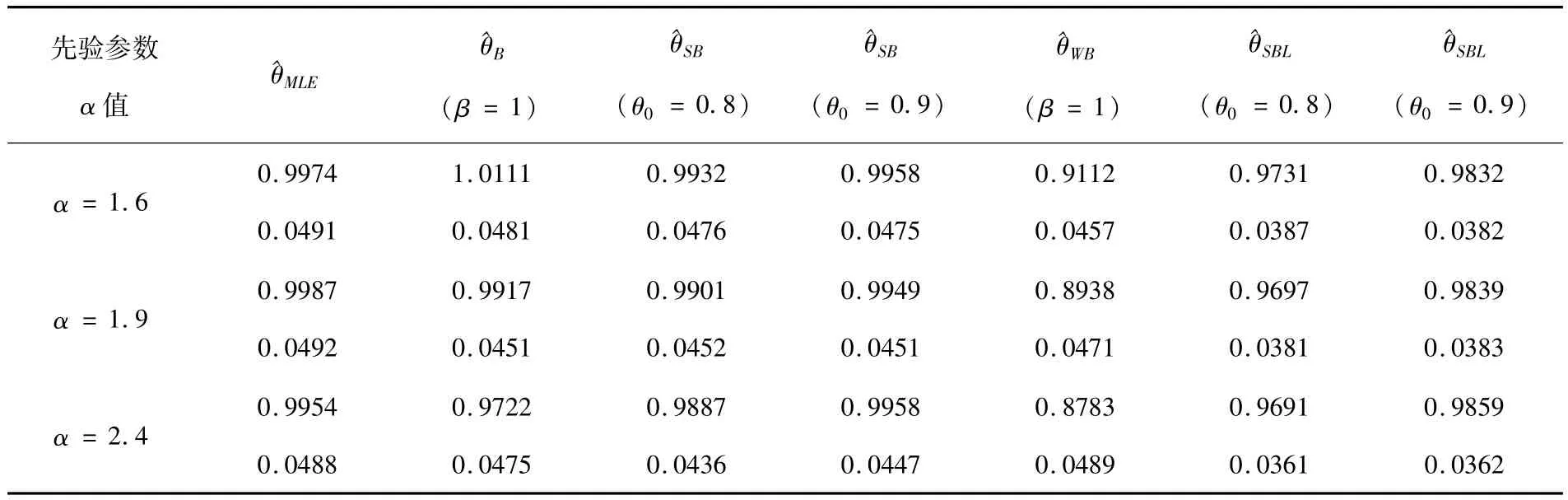
表1 參數的MLE、Bayes及Bayes收縮估計值和相應的均方誤差(c=1)
從表1及大量的數值模擬試驗我們得到如下結論:
(1)當Bayes估計受兩個超參數的影響,而Bayes收縮估計由于不但利用了參數先驗值θ0,而且僅受一個超參數的影響時,若實際中我們得到的參數先驗值θ0較接近真值,Bayes收縮估計相對Bayes估計而言穩健性更好,因而推薦使用Bayes收縮估計方法對參數進行估計;
(2)當樣本容量n較大時,各類估計均較接近真實值.
本文在假定壽命分布服從廣義Pareto分布(2)情況下,取得了未知參數的最大似然估計,并在平方誤差以及LINEX損失函數下得到了參數的Bayes估計和Bayes收縮估計.本文所提出的收縮估計法可以推廣到諸如指數分布、Weibull分布、Burr Type XII分布等壽命分布模型.
[1]Pickands J.Statistical inference using extreme order statistics[J]. Annals of Statistics,1975,(1):119-131.
[2]Rasmussen P F.Generalized probability weighted moments:Application to the generalized pareto distribution[J].Water Resources Research,2001,(6):1745-1751.
[3]趙旭,程維虎,李婧蘭.廣義Pareto分布的廣義有偏概率加權矩估計方法[J].應用數學學報,2012,(2):321-329.
[4]Ashkar F,Tatsambon N C.Revisiting some estimation methods for the generalized pareto distribution[J].Journal of Hydrology,2007,(6):136-143.
[5]Thompson JR.Some shrinkage techniques for estimating the mean[J].Journal of American Statistical Association,1968,(321):113-122.
[6]Qabaha M.Ordinary and Bayesian shrinkage estimation[J].An-Najah University Journal for Research,2007,(1):101-116.
[7]Prakash G,Singh D C.A Bayesian shrinkage approach in weibull type-II censored data using prior point information[J].Revstat-Statistical Journal,2009,(2):171-187.
[8]Prakash G,Singh D C.Bayesian shrinkage estimation in a class of life testing distribution[J].Data Science Journal,2010,8:243-258.
[9]Varian H R.A Bayesian approach to real estate assessment[A]. Studies in Bayesian Econometrics and Statistics in Honor of Leonard JSavage[C].Amsterdam,1975.
Estimation of Parameter of Generalized Pareto Distribution Based on Shrinkage Technique
CHEN Zhaoren1,LIUWanzhen2
(1.College of Engineering and Design,Hunan Normal University,Changsha Hunan 410081,China;2.Changsha Vocational&Technology College,Changsha Hunan 410010,China)
The generalized Pareto distribution is extensively used in the field of finance,insurance,etc.The statistical inference for the distribution has been a hot spotof research.The aim of this paper is to study the Bayes estimation of the parameter of the parameter of the generalized Parato distribution based on the parameter prior is inverse Gamma distribution.Under squared error loss and LINEX functions,Bayes and shrinkage estimators are obtained,and Monte Carlo simulation experiment and conclusion is given at last.
generalized Pareto distribution;Bayes estimation;shrinkage estimator;loss function
O212.8
A
1008-4681(2014)02-0001-04
(責任編校:晴川)
2013-12-18
陳兆仁(1965-),男,湖南長沙人,湖南師范大學工程與設計學院副教授.研究方向:Bayes統計、模糊決策.

