Dijkstra算法與旅游路徑優化

樊守偉， 嚴 艷， 張少杰， 田澤民

(陜西師范大學 旅游與環境學院, 陜西 西安 710062)

Dijkstra算法與旅游路徑優化

樊守偉， 嚴 艷， 張少杰， 田澤民

(陜西師范大學 旅游與環境學院, 陜西 西安 710062)

基于旅游業快速發展的事實，為滿足游客省時、省錢、走最短路程的線路需求，對Dijkstra算法加以改進，即先利用Dijkstra算法依次求出局部最優解，然后整合得到全局最優路徑，從而使改進算法更適合線路設計。最終在綜合考慮旅游花費、交通時間、游覽路程3個因素的前提下，以西安市及周邊景點為例，設計出3種自駕車旅游最優路徑方案，驗證了新算法的可行性。

Dijkstra算法；自駕游；旅游線路

隨著自駕游如火如荼的發展，越來越多的游客參與到自駕游中。自駕車旅游者追求以最少的花銷走更遠的路、看更精彩的風景，并稱為“窮游”，其旅游活動具有多目的地性特征。旅游線路是旅游者在目的地區域內的空間移動軌跡，即旅游空間行為路徑[1]。如何設計出一條多景點間距離最短(或費用、時間最少)的旅游線路是自駕車游客的現實需求[2]。這是一個典型的TSP(Traveling Salesman Problems)問題，即必須訪問版圖上所有城市, 每次經過一個, 最終回到出發點, 給定所有城市之間的旅費, 應該如何計算線路以獲得最小開銷[3]。

TSP問題可通過多種方法解決。最容易的方法是窮舉法，但當所要計算的地點數量較多時，求解就顯得異常復雜、難以實現。常用的智能算法有遺傳算法、蟻群算法、模擬退火算法、人工神經網絡等。遺傳算法程序簡單、易于實現，能夠并行化，但卻存在早熟現象、局部尋優能力較差等問題，所以當針對一些特殊問題時，常規遺傳算法并不一定是最佳選擇。蟻群算法是由Dorigo提出，在解決TSP問題中得到廣泛應用[4]。該算法不僅是一種自適應、自組織、并行的方法，而且可實現正向反饋，能夠促使整個系統向最優解進化；但存在收斂慢、易于陷入局部最優等缺點。模擬退火算法是由Patrick將退火思想引入組合優化領域所提出一種求解大規模組合優化問題的算法[5]。該算法具有較強的局部尋優能力，并能使搜索過程避免陷入局部最優解；但它把握整個搜索過程的能力不夠，不僅使得模擬退火的運算效率不高，而且也難以控制參數溫度的初始值、退火速度問題、溫度管理等問題[6]。Hopfield和Tank于1985年利用人工神經網絡求解TSP問題[7]。該算法在大多數情況下可以求出最優解的近似解；但當城市數大于30時，其求解結果不太令人滿意；當城市規模更大時，易于收斂到非法解或局部極小解，同時還存在收斂速度慢、對模型參數和初始條件敏感等缺點[8]。

而貪心算法中的Dijkstra(迪杰斯特拉)算法被認為是目前求最短路徑問題的最好方法[9]，屬于典型的單源最短路徑算法，是交通網絡最短路徑算法的首選[10]，成為解決旅游交通中線路優化設計的重要方法；但其在旅游業中的應用并不完善，研究層次也較低[11]。故本文在Dijkstra算法基礎上進行改進，即先利用Dijkstra算法依次求出局部最優解，然后整合得到全局最優路徑，并以西安市周邊景點為例，結合自駕車游客的特點，對西安市周邊的自駕車旅游線路進行優化設計。

1 算法介紹及改進

1.1 Dijkstra算法

Dijkstra算法的基本思想是：設集合V是圖G的頂點集合，集合S存放已經找到最短路徑的頂點，初始狀態時，集合S中只包含源點vi然后不斷地從S集合以外的所有頂點集合VS中選擇到源點vi路徑長度最短的頂點vj加入到集合S中，集合S中每加入一個新的頂點vj都要修改從源點vi到VS集合中剩余頂點的當前最短路徑長度值，集合VS中各頂點的新的當前最短路徑長度值，為原來的最短路徑長度值與從源點經過頂點vj到達該頂點的路徑長度中的較小者。此過程不斷重復，直到集合V中的全部頂點都加入到集合S中[12]。

1.2 Dijkstra算法在TSP問題中的改進應用

由于Dijkstra算法是單源最短路徑算法，該算法不能解決全通拓撲結構圖中的TSP問題，故只利用該算法尋找局部最短路徑，從而形成全局最優路徑。

假設集合S1存放已經找到最短路徑的頂點，開始時，利用Dijkstra算法得出起點v0到所有景點的最短距離，然后，找到最短距離中的最小數值

dist[j]=min{dist[i]|(vi∈VS)}，

并把i并入到集合S1中，在以j為起點再利用Dijkstra算法計算到集合VS1所有最距離中的最小值，直到集合VS1為空集為止。其實現流程如圖1所示，實現步驟如下。

步驟1 初始時，S1只包含起點v0，VS1包含除v0外的其他頂點。然后，執行Dijkstra算法，得到從v0出發到其余各頂點可能達到的最短路徑長度的初值為

dist[i]=cost[v0,vi](vi∈V)。

步驟2 選擇vj，使

dist[j]=min{dist[i]|(vi∈VS)}，

vj就是當前求得的一條從v0出發的最短路徑的終點，將vj并入集合S1。

步驟3 令以vj為出發點，執行Dijkstra算法，得到{dist[i]|(vi∈VS)}。

步驟4 重復步驟2和步驟3，直至集合VS1為空集，依次輸出各景點序號，形成每相鄰兩景點都是最小距離的旅游線路。

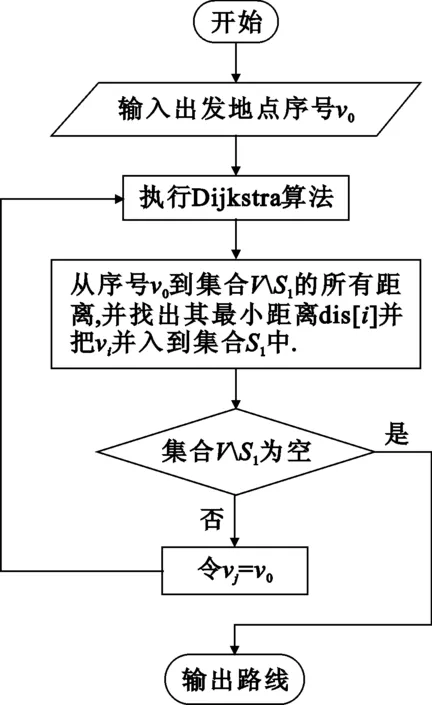
圖1 程序流程

2 案例背景及實際數據

2.1 案例背景

西安市旅游資源豐富，自駕游發展勢頭強勁。為使研究樣本具有代表性，通過對西安自駕車游客訪談，選定西安市及其周邊深受自駕車游客喜愛的10個景點分析，這10個景點為鐘樓(與鼓樓、回民街、城墻列為一處景點)、乾陵、法門寺、碑林、陜西歷史博物館、大雁塔、大唐芙蓉園、兵馬俑、華清池、華山，并分別記為Xi(i=1,2,…,10)。

假定自駕游均以私家車為交通工具，以高速公路和非高速公路為主要道路，車速一定，路況通暢，天氣等一切突發情況不納入考慮范圍，同時默認各景點之間回程與去程有多條路徑。

2.2 數據來源

2.2.1 旅游景點加權圖

利用Dijkstra算法進行線路優化設計時，首先需將旅游地圖轉化為加權有向圖。本文對加權有向圖做了調整，圖中只標出線路，具體權值在下文給出。將每個旅游景點看作加權有向圖的一個節點，景點間的交通線路作為邊，各景點間的距離(或行程時間、交通費用)是對應邊的權值。

2.2.2 旅游景點線路權值

(1) 距離權值

利用ArcGIS軟件，首先將景點間的線路進行數字化處理，其次通過舍遠取近法找出最短線路，最后利用比例尺轉化得到景點間具體距離。最終得出距離權值表(表1)。

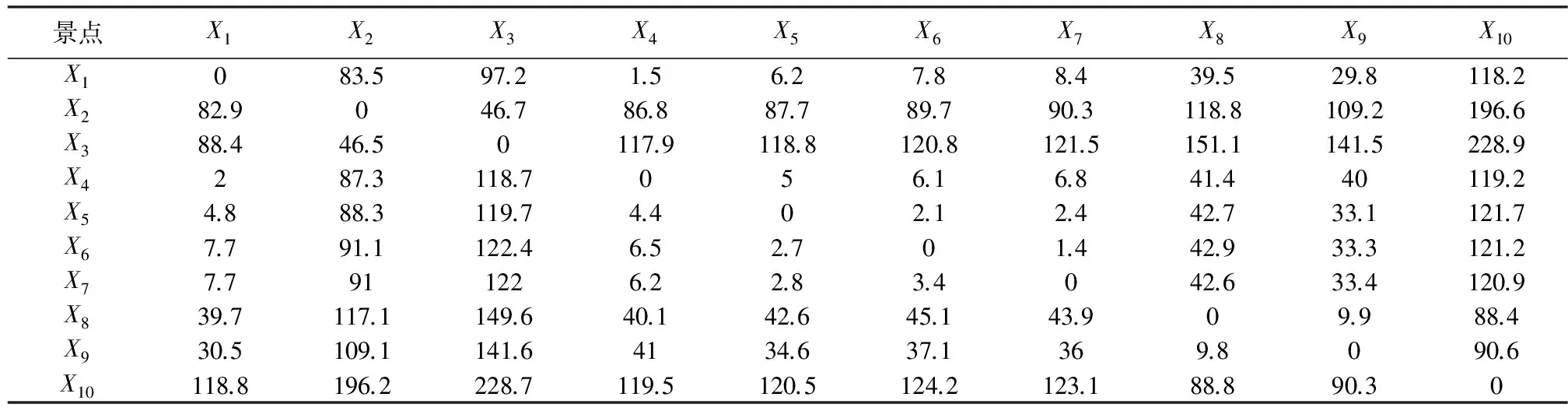
表1 景點間距離權值表 /km

注 只考慮各景點之間的距離，而景區內的距離未列入考慮范圍。

(2) 時間權值

前文已假定車速一定，路況良好，可由各景點間的實際距離計算出其交通時間，從而將時間最短問題表現為具體路徑問題。但最近的線路未必是最省時的，比如存在道路崎嶇、彎道較多不易于行駛等問題。故本文權衡景點間各條線路的路況、距離、實際情況等選擇線路，以保證路途中用時是最少的。最終得出時間權值表(表2)。

表2 景點間駕車時間權值表/min

注 只考慮各景點之間的交通時間，而景區內的游玩時間未列入考慮范圍。

(3) 費用權值

旅游費用涵蓋“食住行游購娛”6方面，其中只有“行”是比較可控的，其余5項因主觀性較大、不確定因素多、與所訪景點次序無關等因素而不考慮。交通費用與公路等級、燃油費等有關，本文按照高速公路0.6 元/車·km及燃油費0.7 元/車·km的標準計算，同樣將無形的費用問題轉化為具體路徑問題。首先根據景點間的線路分別計算出所需的交通費用，再結合所花交通費用最少的原則確定線路，最終得出費用權值表(表3)。

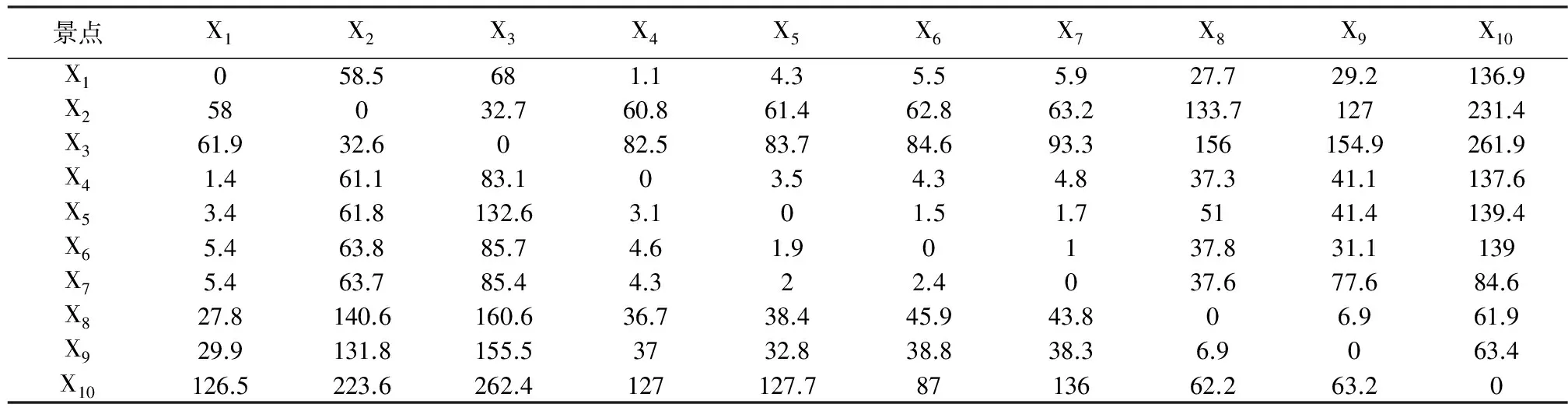
表3 交通費用權值表/元

3 算法應用

利用上述景點間距離、駕車時間、交通費用等數據，在C語言環境中運行所改進的程序進行線路設計，得到如下結果。

3.1 最短路程路線

當不限定交通費用與時間、只考慮最少駕車路程時，最佳旅游線路是

X1→X4→X5→X6→X7→X9→
X8→X10→X2→X3→X1,

相對應線路為

鐘樓→碑林→陜西歷史博物館→
大雁塔→大唐芙蓉園→兵馬俑→
華清池→華山→乾陵→法門寺。

該線路行程共354.3 km。

3.2 最省時間路線

當不限定交通費用與路程時、只考慮所用駕車時間最少時，最佳旅游線路是

X1→X4→X5→X7→X6→X9→
X8→X10→X2→X3→X1,

相對應線路為

鐘樓→碑林→陜西歷史博物館→
大唐芙蓉園→大雁塔→兵馬俑→
華清池→華山→乾陵→法門寺。

該線路途中用時373 mins。

3.3 費用最少路線

當不限定時間和路程、只考慮交通費用最少問題時，最佳旅游線路是

X1→X4→X5→X6→X7→X8→
X9→X10→X2→X3→X1,

相對應線路為

鐘樓→碑林→陜西歷史博物館→
大雁塔→大唐芙蓉園→華清池→
兵馬俑→華山→乾陵→法門寺。

該線路駕車交通費用為 289.7 元。

4 結語

將Dijkstra算法應用到自駕游線路設計中，所設計的線路可滿足自駕車游客的需求，方法具有普適性且實現簡單。未來應用中，可建立全國最優旅游路徑網站或旅游線路查詢決策系統。旅游區旅游線路的開發水平、完善程度，起到把握控制旅游流的流量、流向的作用，因此，相關結果可擴展到區域旅游交通規劃和景區內道路設計等實際應用方面，可據實際需要進行改進，為旅游相關部門提供決策支持。據此最優路徑制定的旅游開發戰略可推動沿線地區旅游業的進步，對區域經濟的發展具有深遠意義。

[1] Lue C C, Crompton J L, Stewart W P. Evidence of cumulative attraction in multidestination recreational trip decisions[J]. Journal of Travel Research,1996,35(1):41-49.

[2] 滕聰,曹文.旅游景點篩選組合及旅游線路的優化算法與應用[J].地球信息科學學報, 2010,12(5):668-673.

[3] 許麗佳,蒲海波,蔣宏健.改進遺傳算法的路徑規劃研究[J].微計算機信息, 2006,22(2):251-253.

[4] Kan Junman, Zhang Yi. Application of an Improved Ant Colony Optimization on Generalized Traveling Salesman Problem[J]. Energy Procedia, 2012,17(4): 319-325.

[5] Zhang Jin, Liu Huaishan, Tong Siyou, et al. The improvement of ant colony algorithm and its application to TSP problem[C]//5th International Conference on Wireless Communications, Networking and Mobile Computing. Beijing:IEEE,2009:1-4.

[6] 高尚. 求解旅行商問題的模擬退火算法[J].華東船舶工業學院學報,2003,17(3):13-16.

[7] Hopfield J J, Tank D W. “Neural” computation of decisions in optimization problems[J]. Biological Cybernetics,1985,52(3):141-152.

[8] 王潮, 宣國榮.人工神經網絡求解TSP問題新方法[J].計算機應用與軟件,2001,18(4):59-64.

[9] 王佳,趙宏麗.基于Dijkstra算法的京津冀旅游交通線路優化研究[J].統計與決策, 2011,337(13):82-83.

[10] 陸鋒. 最短路徑算法: 分類體系與研究進展[J]. 測繪學報, 2001, 30(3):269-275.

[11] 吳凱. 旅游線路設計與優化中的運籌學問題[J]. 旅游科學, 2004, 18(1):41-44.

[12] 熊回香.數據結構:C/C++版[M].北京:清華大學出版社,2010:292-302.

[責任編輯:王輝]

The optimal route design for self-driving travel
based on the Dijkstra algorithm

FAN Shouwei, YAN Yan, ZHANG Shaojie, TIAN Zemin

(School of Tourism and Environment, Shaanxi Normal University, Xi’an 710062, China)

An improved scheme based on the Dijkstra algorithm is proposed to meet rapid development of tourism with high demand from self-travelers on tourism routes design for reduced cost and traffic time as well as the tour distance. This scheme can find out the local optimal path in order to achieve the global optimal path. Three optimal paths about self-driving travel in Xi’an given through this scheme are proved to be feasible.

Dijkstra algorithm, self-driving travel, tourism routes

10.13682/j.issn.2095-6533.2014.01.025

2013-11-23

陜西省社會科學基金資助項目(13Q045)

樊守偉(1988-)，女，碩士研究生，研究方向為旅游景區規劃與管理。E-mail：1025443824@qq.com 嚴艷(1968-)，女，博士，副教授，從事旅游管理與人文地理等研究。E-mail：yanyan@snnu.edu.cn

F590

A

2095-6533(2014)01-0121-04