廣義預測控制在非線性系統中的應用研究

王麗飛，劉洪娥，于佐軍（中國石油大學，山東 青島 266555）

1 引言

廣義預測控制是Clarke等人在1987年針對工業過程的特點，在保持最小方差自校正控制的在線辨識、最小方差控制的基礎上，吸取了DMC和MAC中的滾動優化策略，提出的一種新型的計算機控制。廣義預測控制具有諸多優點：首先，它是基于參數模型的，而其他的預測控制算法大部分是基于非參數模型的。其次，它保留了自適應控制的優點，而且較自適應控制有更好的魯棒性。最后，由于采用多步預測、滾動優化和反饋校正等策略，其控制效果更適應工業過程控制的要求[1～3]。由于這些優點，廣義預測控制一出現就受到了控制界和工業界的廣泛關注，其理論研究不斷深入，并在很多工業過程中得到應用，取得了較好的控制效果[4]。

但是，目前廣義預測控制的研究對象大部分是線性離散時間系統，對非線性系統廣義預測控制的研究，由于難于構造被控對象的多步預報模型因而導致廣義預測控制律求解困難。目前非線性系統的廣義預測控制一般都是用神經網絡的方法來獲得被控對象的多步預測值，這種方法需要首先訓練神經網絡，其模型不能進行在線辨識[5～7]。本文針對一類比較具有普遍意義的非線性系統，首先將其轉化為時變參數的線性系統，然后使用具有遺忘因子的最小二乘法或是多項式逼近法在線辨識模型參數，進行廣義預測控制。并以二容液位系統為模型，進行了仿真研究，取得了較好的控制效果。

2 非線性系統的廣義預測控制

2.1 非線性系統模型及其等效時變線性系統

非線性系統被控對象的輸入輸出模型可以描述如下：

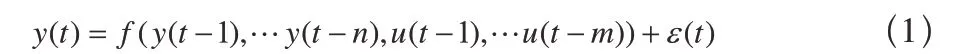
其中 u、 y分別表示系統的輸入、輸出，m、n分別表示輸入輸出階次，ε(t)表示噪聲干擾， f(?)是未知的關于y(t ?1),y(t?n),u(t?1),u(t?m)的非線性函數，并且滿足下列條件：

（1） 0)0,0,0( =f

（2） f (?)關于y(t ?1),y(t?n),u(t?1),u(t?m)連續可導，且各偏導數有界。

條件（1）要求系統的平衡點為零點，若不滿足此條件，可通過坐標變化使之滿足此條件，條件（2）代表了一類非線性系統，也是許多實際非線性系統過程所滿足的。這兩個條件并不是很苛刻，對這類非線性系統的研究也具有實際意義。可以證明[8～9]，滿足以上兩個條件的非線性系統可以等價地表示為如下的時變線性系統：

并且 ai（i = 1,2,n ）、bj（ j = 1,2,n） 是有界的。這一時變線性系統相當于將非線性系統等價為一個由無數線性系統組成的線性模型的集合，每一時刻對應集合中的某個線性模型。

根據以上論述，我們就可以在廣義預測控制的每一步，先辨識非線性系統的線性化模型，然后再進一步求解廣義預測控制律。

2.2 模型參數的辨識

式（2）是由一個非線性系統等價而來的參數未知的時變線性系統，當非線性系統不是處在穩定工作點時，其等價的時變線性系統的參數是不斷變化的，因此，要對系統進行控制，就必須先辨識系統模型的參數（在系統的階次已知的情況下），要辨識的模型如下：

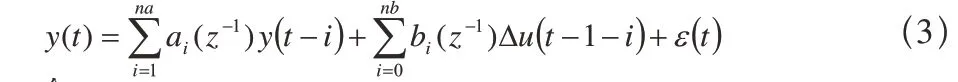
令：

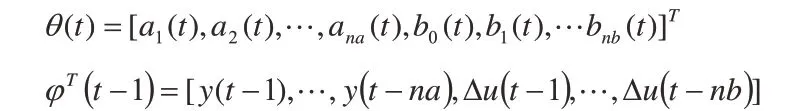
則式(3)可表示為：

對于以上時變系統模型的辨識，如果參數屬于慢時變的，可以采用改進的線性定常系統的辨識方法，本文采用具有遺忘因子的最小二乘法，其計算公式如下：

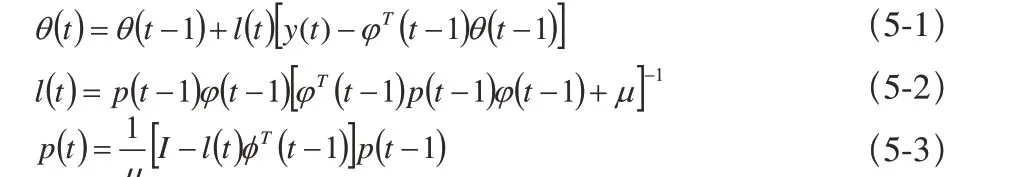
其中， 0 <μ ≤1是遺忘因子，一般可取 0 . 95<μ ≤1， l (k )為權因子， p ( k )為正定的協方差陣。θ 與p的初值可用一次完成的最小二乘法得到，或直接選為

如果時變參數變化較慢，采用上述具有遺忘因子的最小二乘法就能獲得較好的效果，但在參數變化較快的情況下，參數的辨識應該依據對應時刻的觀察數據，不能過多地使用過去時刻的觀測數據，因此很難滿足時變參數辨識時對觀察數據充分豐富的要求，使用上述算法就存在較大的誤差，為了解決該問題，比較常用的是多項式逼近法。所謂多項式逼近方法，就是將時變序列展開成多項式基函數的線性組合形式，通過辨識這些線性組合的定常系數來實現時變參數的辨識。

對于式(3)中 )(tθ 的任意一個元素，在任意一個時間間隔 ],[21ttt ∈ 上，存在多項式：

通過引入如下一個變量代換[10～11]

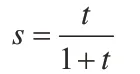
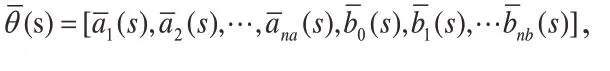
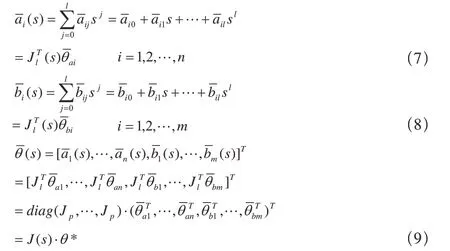
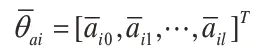
則式(3)可以寫成：

)(tξ 為系統的噪聲與多項式的截斷項所造成的未建模動態誤差之和。

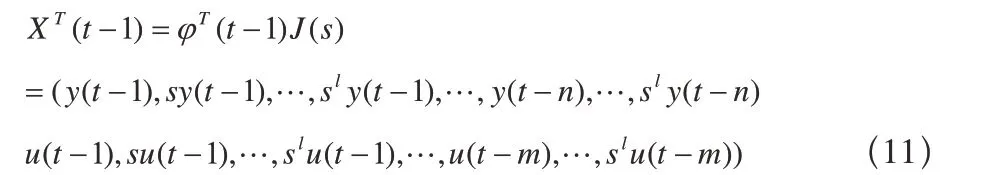
對(10)進行辨識時，先進行正則化處理：

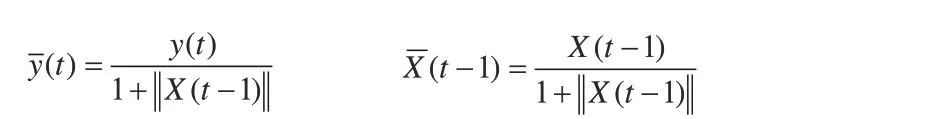
即：

對上式中的參數采用如下帶有死區的最小二乘算法進行辨識：

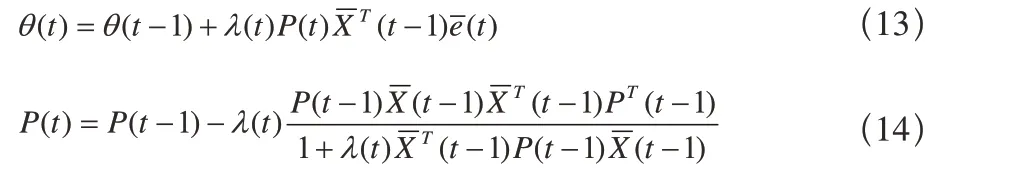
死區切換函數定義為：

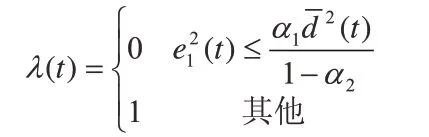
其中，α1=1+trace(P(0))， t rP (0)表示矩陣 P (t)在時刻等于 t =0時的跡，α2為小于1的任選正常數。

2.3 非線性系統工作點變化時的廣義預測控制

在實際的過程中，大部分的非線性系統都是工作在某一穩定工作點上，因此，系統穩定運行時，可以將系統作為一個時不變線性系統進行控制，而當系統的工作點變化的時候，就需要采用上面所論述的原理，將非線性系統等價為時變的線性系統，在線辨識模型參數，并進行廣義預測控制，使系統由一個工作點快速平穩地達到另外一個工作點。

非線性系統工作點變化時的廣義預測控制的步驟：

（1）如果非線性系統工作在同一工作點，轉到3，否則執行2；

（2）用具有遺忘因子的遞推最小二乘法（參數變化緩慢）或多項式逼近時變參數的方法估計模型參數 )(tai， )(tbj；

（3）求解Diophantine方程，計算jE、jF、jG、jH；

（4）計算矩陣G和G ( G + λ I )?1；

（5）求解控制量 )(tu ；

（6）返回到1，繼續執行；

此處需要說明的是，如果用具有遺忘因子的遞推最小二乘法辨識參數，那么它與線性系統廣義預測控制中的具有遺忘因子的遞推最小二乘法雖然都是用來估計系統的參數，但意義并不相同，前者求的是非線性系統在不同工作點附近的線性化的模型參數，目的是使線性化后的模型能盡可能逼近非線性模型，參數變化比較大；后者求的是線性系統的模型參數，它的作用是使辨識值不斷地接近線性系統模型參數的真實值，參數變化不大。此外，如果非線性系統是由一個工作點運行到令一個工作點時，辨識的初始值應該設為起始工作點線性化后的模型參數。

3 廣義預測控制在二容液位系統中的應用

3.1 二容液位控制系統的建模

二容液位系統如圖1所示：

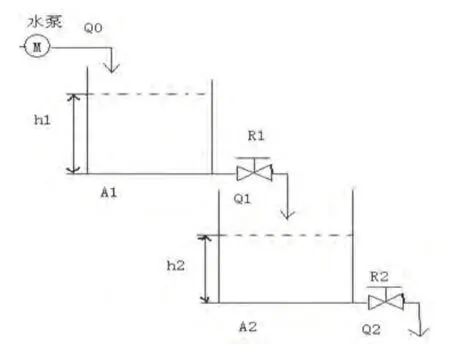
圖1 二容液位圖

在圖1中，上面的容器稱為容器1，下面的容器稱為容器2。容器1的水流輸入量Q0是由水泵M決定的，水泵的正常工作區間為0-3 m3/h，即水泵能夠提供的最大水流為 1 /1200m3/s。容器1的水流輸出量Q1與容器1的液位高度的開方成正比，即 Q1 = k 1h1，同理，容器2的水流輸出量Q2與容器2的液位高度的開方成正比，即，則根據物料平衡方程：

容器內儲液量的變化率 = 單位時間內液體流入量 - 單位時間內液體流出量

可以得到容器1的液位：

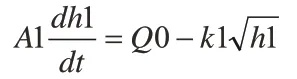
容器2的液位：

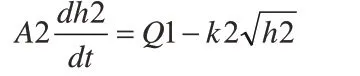
其中的A1，A2分別為容器1、容器2的橫截面積。

3.2 二容液位系統的仿真

在二容液位系統的仿真研究中，以容器1的水流輸入量作為輸入控制量，以容器2的液位高度作為輸出控制量，系統用CARMA表示，即

采用具有遺忘因子的最小二乘法辨識模型的參數。系統的仿真輸出采用四階龍格—庫塔法得到，其公式如下：

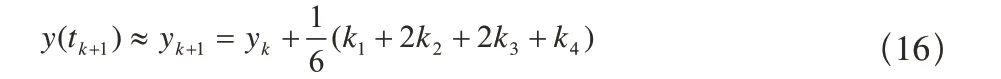
其中：

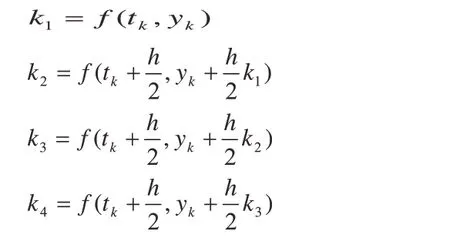
f( t,y)為系統的模型。

3.3 仿真結果

系統在幅值為7.8881e-004的階越響應下的響應曲線如圖2所示：

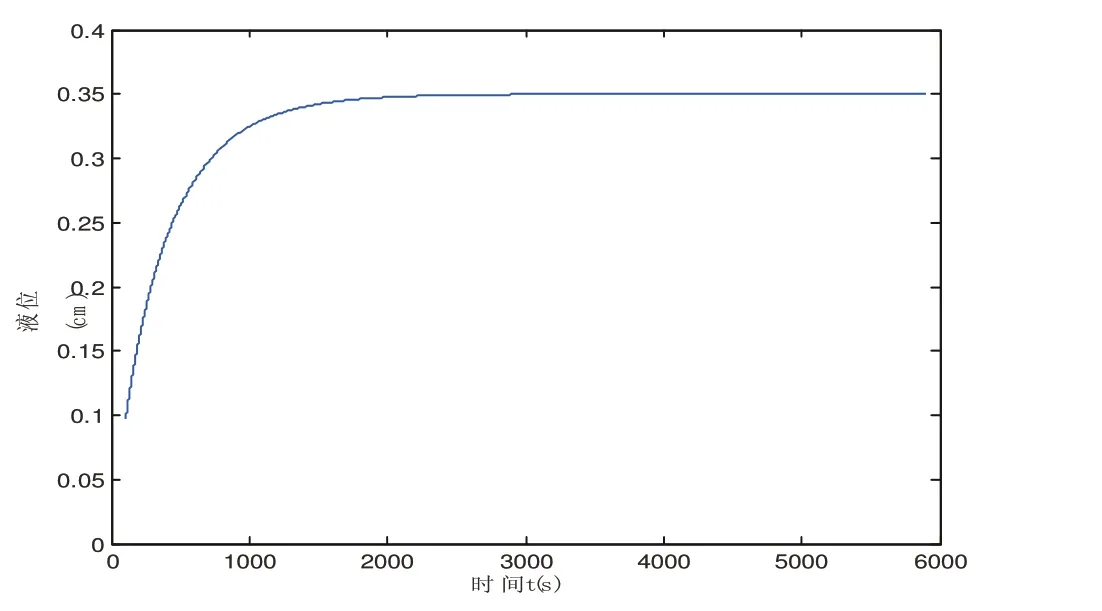
圖2 階躍響應曲線

初始液位為0，液位設定值為0.35m，采用具有遺忘因子的最小二乘法辨識系統模型，其仿真結果如圖3所示：

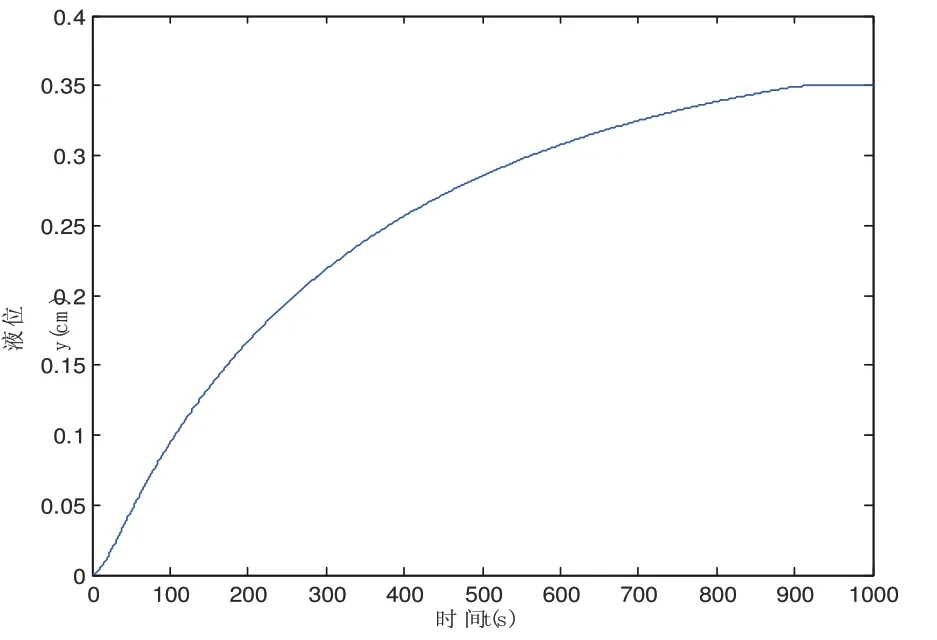
圖3 具有遺忘因子的最小二乘法辨識系統模型的輸出曲線

采用多項式逼近法辨識模型參數時，其仿真結果如圖4所示：

由圖3和圖4可以看出，由于參數變化比較緩慢，無論是采用多項式逼近法辨識模型還是采用具有遺忘因子的最小二乘法辨識模型，輸出曲線相差不大，都能實現非線性系統工作點的切換。

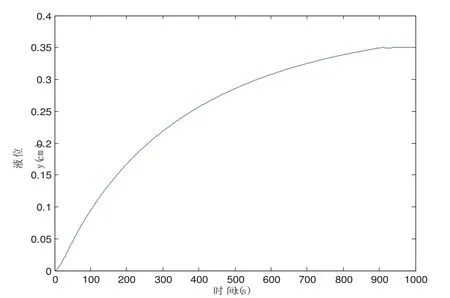
圖4 多項式逼近法辨識模型的輸出曲線

4 結語

本文針對一類比較具有普遍意義的非線性系統，首先將其轉化為時變參數的線性系統，然后使用具有遺忘因子的最小二乘法或是多項式逼近法在線辨識模型參數，進行廣義預測控制，給出了兩種辨識時變參數的方法，并以二容液位系統為模型，進行了仿真研究。結果表明，使用具有遺忘因子的最小二乘法或是多項式逼近法在線辨識模型參數，輸出曲線相差不大，都能實現非線性系統工作點的切換。

[1] 孫洪濤. 廣義預測控制的應用研究[D]. 天津: 天津大學, 2006.

[2] 師五喜. 廣義預測控制中Diophantine矩陣多項式方程的顯示解[J]. 控制理論與應用. 2007, 24 (2) : 261 - 263.

[3] Xu Zuhua, Zhu Yucai, Han Kai, Zhao Jun, Qian Jixin. A multi-iteration pseudo-linear regression method and an adaptive disturbance model for MPC [J]. Journal of Process Control, 2010, 20 (4) : 384 - 395.

[4] 張月靜, 徐喆. 基于廣義預測控制的儲罐液位系統的仿真分析[J]. 當代化工, 2013, 42 (11) : 1605 - 1607.

[5] 張敏杰. 改進廣義預測控制算法的研究[D]. 太原: 太原理工大學, 2012.

[6] 李奇安, 邵明新, 李悅. 基于遺傳算法的多變量增量型廣義預測控制[J]. 江南大學學報 (自然科學版) , 2013, 12 (5): 626 - 630.

[7] Jiang Jian-hua, Li Xi, Deng Zhong-hua, Yang Jie, Zhang Yisheng. Thermal management of an independent steam reformer for a solid oxide fuel cell with constrained generalized predictive control[J]. International Journal of Hydrogen Energy, 2012 (37) : 12317 - 12331.

[8] 郭健, 朱瑞軍, 胡維禮. 一類非線性系統的自適應廣義預測控制[J]. 控制與決策. 2001, 16 (3) : 358 - 361.

[9] 李奇安, 金鑫. 對角CARIMA模型多變量廣義預測近似解耦控制[J]. 浙江大學學報 (工學版) , 2013, 47 (10) : 1764 - 1769.

[10] L Guo. Estimating time varying parameters by the Kalman filter based algorithm: Stability and convergence[J].IEEE Trans on Autom Contr, 1990, 35 (2): 141 - 147.

[11] 李德權. 線性時變系統的辨識及其應用研究[D]. 南京: 東南大學, 2003.