湍流轉捩工程預報方法研究進展綜述

張 雯，劉沛清，郭 昊，屈秋林

（北京航空航天大學，北京100191）

湍流轉捩工程預報方法研究進展綜述

張 雯，劉沛清，郭 昊，屈秋林

（北京航空航天大學，北京100191）

湍流轉捩現象對邊界層流動的阻力和熱交換特性具有嚴重影響。準確地預測轉捩對工程設計意義重大。近年來發展迅速的轉捩模型是一種非常適合工程計算的轉捩預報方法。本文將轉捩模型分成了4個類型，并對每種轉捩模型的發展過程加以闡述。在分析和討論的基礎上，總結了目前轉捩模型的發展水平，同時也指出尚存的不足之處，為將來構建新的轉捩模型以及相關的轉捩研究提供建議。

轉捩；轉捩模型；工程計算；低雷諾數；間歇因子；層流脈動；不穩定波

· 編者按 ·

為打造更好的學術交流平臺，促進實驗流體力學學科發展，根據王晉軍副主編提議和推薦，編輯部進行了專題約稿，并在本期開設了“湍流和流動控制”熱點專欄。在此對積極撰稿、認真審稿等給予本刊大力支持和幫助的專家、作者表示衷心感謝！

0 轉捩現象及其預報概述

邊界層轉捩伴隨著壁面摩擦和熱交換特性的急劇變化，對于飛行器［1］、燃氣渦輪發動機［2］等工程設計有重要的意義。轉捩過程的物理機制復雜、影響因素眾多，所以邊界層轉捩長期以來一直是流體力學中的熱門課題，至今仍有許多問題尚待解決。

邊界層流動往往受到包括壁面粗糙度、自由來流湍流度、壓力梯度、三維流動、壁面溫度、壁面曲率、馬赫數等多種因素的影響。流動條件不同，從層流到湍流轉捩的機制也不甚相同。低速邊界層流動的轉捩可以分成2類：第1類與邊界層的不穩定性相關，當環境擾動較低時，不穩定性發展放大、相互作用，并最終導致轉捩；第2類轉捩被稱為Bypass轉捩，在環境擾動（來流湍流度、壁面粗糙度）較高時，直接由外部擾動導致層流發生轉捩［3］。在飛機巡航的低湍流度（0.03%～0.05%）高空大氣環境下，機翼上可能出現T-S（Tollmien-Schlichting）轉捩、橫流（Crossflow）轉捩、Gotler轉捩和接觸線（Attachment-line）轉捩［4］。在燃氣渦輪發動機中，來流湍流度一般在5%到10%，如果葉片剛好處在上一級葉片的尾跡中時，來流湍流度可以達到15%到20%［5］，邊界層轉捩以Bypass轉捩為主。高速可壓縮流動中，除了存在低速流動中出現的不穩定性之外，聲波對邊界層的穩定性具有顯著影響［6］。在平板或翼型的前緣，即沿程雷諾數很低的位置上，聲波因邊界層對其有較強的感受性而誘發出F模態與S模態。這2種模態發展到一定雷諾數的位置上后出現相速度同步。在2種模態的相互作用下，S模態迅速失穩形成Mack第二模態而F模態趨于穩定。這類失穩過程的本質是聲波在聲速線反彈而被困在邊界層內，所以要求邊界層外邊界的當地馬赫數大于1才會出現。

轉捩的預測方法是轉捩研究的重要課題，既是現代工程設計中的需求，也是轉捩基礎研究成果的實際應用。轉捩的預測方法有穩定性理論方法、低雷諾數湍流模型法、轉捩模型法等［7］。當然模擬轉捩過程可以用直接數值模擬（DNS）或者大渦模擬（LES），但是其計算量太大（相當于Re9／4），適用于轉捩機制和建模方法的研究而不適用于工程中的轉捩計算［8］。穩定性理論方法基于對擾動控制方程的穩定性分析，以20世紀50年代提出來的半經驗的eN方法［9-10］為典型代表。半經驗eN方法通過線性穩定性理論計算TS波增長的幅度A，當A與初始擾動的幅值之比達到eN倍時，就認為發生轉捩，其中N是一個由表面粗糙度和來流條件決定的經驗參數。即

該方法需要計算擾動在整條流線各個位置上的增長率［5］，這樣就給工程領域中復雜流動的計算帶來了不小的麻煩。不過這種方法因為出現的時間較早，并且經過實踐證明對簡單幾何外形的繞流計算具有一定的實用性，所以直到近幾年還有不少人在進行這方面的工作［11］。

湍流模型的發展和完善促使CFD技術在航空工程中扮演越來越重要的角色。諸多成熟的湍流模型，比如S-A模型［12］、k-ε模型［13］、k-ω模型［14］、雷諾應力模型［15］以及在這些模型的基礎上發展出來的SST模型［16］、v2-f模型［17］等被廣泛地用于可壓縮／不可壓縮邊界層湍流、自由剪切湍流、分離流等各種湍流現象的工程計算。Rumsey＆Spalart［18］對比了SA模型和SST模型對平板、二維翼型、三維機翼在亞聲速／超聲速條件下的計算結果之后，確認經典的高雷諾數湍流模型不具備計算轉捩流動的能力。

以準確表達轉捩前、中、后的流動特性、準確判斷轉捩開始、完成位置為目標，經過多年的嘗試和改進，形成了較為完善的轉捩模型。轉捩模型的出現與發展極大地擴展了湍流模型計算轉捩流動的能力，為工程應用中低雷諾數流動的阻力特性、熱交換特性以及分離特性的評估提供了直接的幫助，為轉捩控制方法的研究提供了快捷的數值實驗平臺。

根據構建模型的思路、方法不同，轉捩模型可以分成4種類型：（1）低雷諾數湍流模型；（2）間歇因子模型；（3）層流脈動模型；（4）不穩定波模型。下面分別對這4種轉捩模型具體闡述。

1 表征轉捩的低雷諾數湍流模型

帶有轉捩描述的低雷諾數湍流模型出現最早，形式也最簡單。Wilcox的低雷諾數k-ω模型［19］就是這類轉捩模型的代表。早在1975年，Wilcox就提出，如果合理地利用湍流模型中雷諾應力對上游信息的依賴性，則能夠使湍流模型具備預測轉捩的能力［20］。根據他對湍流模型的理解，湍流模型之所以具有計算湍流的能力，一方面，模型方程的構建是從精確的輸運方程出發，對方程各項加以建模得到；另一方面，模型方程中的封閉系數是根據湍流的信息進行確定，比如隨時間衰減的各項同性湍流、具有相似性的壁面邊界層湍流等。

將k-ω模型方程的“產生項”與“耗散項”合并得到“凈產生項”：

Wilcox對上述方程進行了仔細地分析后發現［19］，如果Pk＜0，Pω＜0，耗散項大于產生項，湍動能和耗散率都維持在很低的水平，流動保持“層流”；如果Pk＞0，Pω＜0，湍動能開始增長，而耗散率仍舊維持在較低的水平，流動進行“轉捩”；如果Pk＞0，Pω＞0，湍動能和耗散率都維持在較高的水平，流動進入完全“湍流狀態”。那么Pk=0與Pω=0所對應的雷諾數分別是轉捩開始和轉捩結束的臨界雷諾數。由此，根據實驗測得轉捩開始和轉捩結束的雷諾數，對原本的模型封閉系數進行改造，用湍流雷諾數構造漸近函數：

其中，ReT=μT／μ是湍流雷諾數，Rk，Rω，Rβ是常數。如此改動之后，流動就能在合適的位置“發生轉捩”。此外，Wilcox還加入了壁面粗糙度、來流湍流度、壓力梯度以及可壓縮性對轉捩的影響。

Patel等人使用Wilcox低雷諾數k-ω模型的經驗表明，該模型對于用粗糙帶進行強制轉捩的流動計算效果不錯，同時也注意到該模型得出的轉捩區間長度太短［21］。

為計算轉捩而作低雷諾數修正的還有Launder＆Sharma的低雷諾數k-ε模型［22］。他們的做法是用湍流雷諾數RT修正湍流粘性系數以及耗散率方程中一個封閉系數：

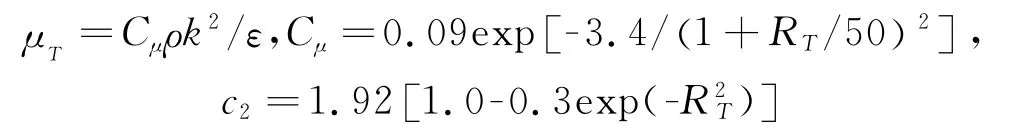
修正之后的模型可以模擬旋轉圓盤上的轉捩流動。

Craft等人［23］的k-ε-A2模型也是對湍流粘性系數的表達式進行了低雷諾數修正。Craft的模型能夠準確模擬零壓力梯度平板邊界層的轉捩，但是對于順壓梯度或者逆壓梯度時轉捩的計算則明顯提前，并且有時候會出現數值不穩定現象［24-25］。

根據Savill的結論，用湍流雷諾數來判斷轉捩開始的效果還是不錯的［26］。總的來說，表征轉捩的低雷諾數修正已經是湍流模型向前邁進的一大步。

考慮到低雷諾數修正的方法與湍流模型本身的性質有著非常緊密的聯系，其轉捩計算結果可能僅僅是一種數值現象［27］，也可以理解是Wilcox從數學的角度證明對模型方程系數的改動可以讓其具有準確計算轉捩的能力。作為模擬轉捩的早期成果，這種轉捩模型意義重大。

國內學者在低雷諾數修正模型中做了較多的研究工作，例如徐星仲［28］、錢煒琪［29］、嚴明［30］、張揚［31］等或將漸進函數引入不同的湍流模型，或改進了漸進函數的表達式，使得湍流模型獲得了一定程度上準確預測轉捩位置的能力，提高了湍流模型在計算流場阻力的準確性。

肖志祥等人在對B-L模型和S-A模型進行修正的過程中注意到，更復雜的S-A模型能夠反映流動參數的細節變化［32］，這一觀點與近年來轉捩模型的發展一致：對湍流模型的改進不僅僅能夠準確預測轉捩發生的位置，而且能夠一定程度上表達轉捩過程中物理量的變化，并且試圖通過準確計算這些物理量的變化過程來更準確地預測復雜流動條件下的轉捩位置和流動特性。

2 表征湍流發生的間歇因子模型

早期的研究就注意到，轉捩總是發生得很突然，并且轉捩位置會前后移動［33］。Emmons［34］提出，轉捩現象實際上是層流邊界層內產生具有湍流特性斑點的過程。這些斑點在層流與湍流的界面上組成粗糙的動態鋸齒形狀，具體到每個位置上的狀態可以用湍流出現的概率進行描述。Emmons關于“湍流斑”的理論，很快被Schubauer＆Klebanoff的實驗［35］證實。Dhawan＆Narasimha［36］根據Emmons的理論，提出用“間歇因子”來定量地描述湍流的產生過程，并根據實驗結果給出了轉捩過程中間歇因子的表達式：

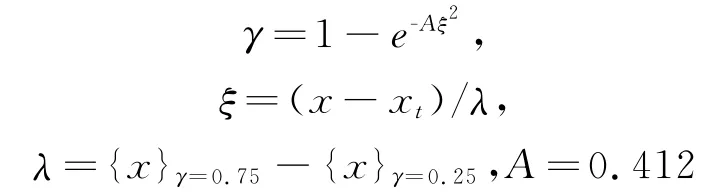
Libby［37-38］根據湍流場邊界的間歇性特點，借助條件平均方法，用帶有間歇因子的輸運方程來計算湍流，以解決湍流模型計算湍流區域與層流區域之間的過渡問題。此前的計算都近似認為到某一位置后流動就陡然從層流變成湍流，由此造成摩擦阻力和邊界層厚度的偏差［39］。Dopazo［40］參照Libby的方法，詳細推導了經過條件平均后流場輸運方程的精確表達式，為湍流邊界標量場的計算奠定基礎。隨后，Chevray＆Tutu［41］通過常規測量和條件測量，對加熱射流的實驗數據進行分析，并以此為基礎推導了動量和能量的帶有間歇因子的條件平均輸運方程。

沿用間歇因子概念，Cho＆Chung［42］用雷諾平均方程，在k-ε模型的基礎上，為間歇因子構建了輸運方程，即k-ε-γ三方程湍流模型，用該湍流模型對平面射流、圓柱射流、平板尾跡和平面混合層進行了計算。盡管并沒有進行邊界層轉捩計算，他們的方法為轉捩模型的發展，尤其是在計算間歇因子空間分布上提供了寶貴的借鑒。Steelant＆Dick［43］對Navier-Stokes方程作條件平均，并構建了描述邊界層轉捩的間歇因子方程，耦合求解，使得轉捩區間間歇因子的流向分布計算結果與Dhawan＆Narasimha給出的間歇因子分布相吻合，但并沒有考慮邊界層法向的間歇因子分布。

Suzen＆Huang［44-45］在SST模型上增加了間歇因子的輸運方程，將Steelant＆Dick與Cho＆Chung的間歇因子方程綜合，同時考慮邊界層中流向和法向的間歇因子分布，計算結果與Savill［46-47］的T3系列邊界層轉捩實驗結果吻合很好。在此之前沒有模型能夠同時準確計算一系列條件下的轉捩位置和轉捩區間的長度。Suzen＆Huang的間歇因子方程如下：

其中，T0是為了重現Dhawan＆Narasimha實驗結果而加入的產生項。轉捩區的計算沿用了Mayle［2］的表達式：

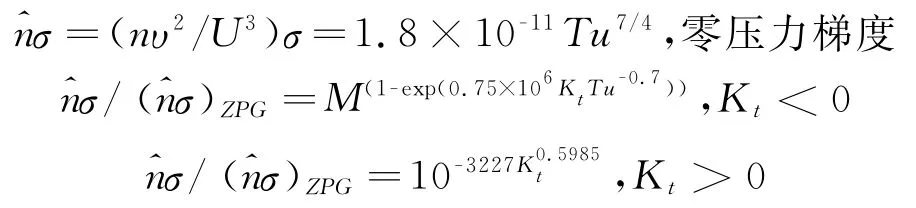
順壓梯度（Kt＞0）的經驗公式來自Steelant＆Dick［43］，逆壓梯度（Kt＜0）的經驗公式來自Gostelow［48］對6種來流湍流度、多種壓力梯度下的轉捩邊界層測量結果的擬合。附著流動轉捩開始位置的計算沿用Abu-Ghannam＆Shaw［49］的經驗公式，以此添加來流湍流度與壓力梯度對于轉捩位置的影響：

壓力梯度參數λθ=（θ2／υ）（dU／ds），

分離流動轉捩位置的經驗公式：

可以看到，Suzen＆Huang的模型已經相當完善，對于來流湍流度、壓力梯度、分離等主要影響因素的考慮已經充分地融入模型中，經驗公式的加入意味著計算轉捩的準確性在一定范圍內得到有效的保證。當然，Suzen＆Huang的間歇因子模型無論是在轉捩區域還是在湍流邊界層的上邊界都能光滑過渡，這也是綜合了前人工作成果才達到的效果。

受Van Driest［50］經驗關系式的啟發，Menter［51］建立了依賴經驗公式的間歇因子轉捩模型，提出“當地量”的轉捩計算方法。此前的模型都或多或少地要對邊界層進行積分。盡管當時的模型不算太完善，這種理念卻影響深遠。Menter＆Langtry［52-53］在SST模型的基礎上附加了間歇因子和動量厚度雷諾數2個輸運方程：

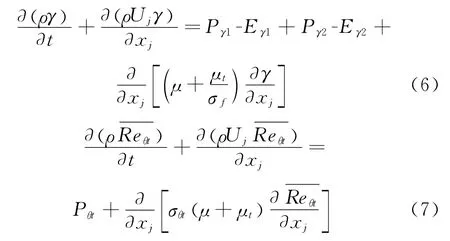
Menter的思路非常清晰：用動量厚度雷諾數來判斷轉捩的開始，用間歇因子來描述轉捩的過程。動量厚度雷諾數原本需要對邊界層的速度進行積分運算才能得到，這里對其進行了抽象，將其當做一個流場的當地量用輸運方程進行計算，所以會看到計算結果中在相同流向位置、不同法向高度位置上的動量厚度雷諾數其實是不一樣的。從方程上來看，空間中某個位置上的動量厚度雷諾數會快速增長，直至達到當地的臨界動量厚度雷諾數為止，而邊界層內卻沒有相應的源項，完全依賴擴散進入邊界層：

間歇因子的產生項則是用當地的渦量雷諾數與計算出來的動量厚度雷諾數進行比較進而確定：

該模型方程通過破壞項／再層流化項把層流邊界層中的間歇因子保持近乎為零并且讓模型具有模擬再層流化現象的能力：

為模擬壓氣機和低壓渦輪中常見的層流分離泡現象，增加了描述分離的間歇因子

與Suzen＆Huang的模型相比，Menter＆Langtry在實現“當地變量”的計算方法中考慮得更加周到。不難發現，其實在Menter＆Langtry的四方程轉捩模型中，并沒有完全摒棄湍流雷諾數RT這樣一種簡單的、多年以前就在使用的轉捩判斷依據。

一方面，使用當地量對于工程應用的意義非常重大，比如并行計算、非結構網格和復雜流動問題，Menter、Langtry［54-56］也是多次強調；另一方面，基于經驗公式的構建思路優勢非常明顯，不用做太多的修改就可以移植到其它人現有的成熟CFD代碼上、與其它湍流模型進行整合、添加其它轉捩機制的經驗公式進入模型。Menter的成果很快得到了業界的認可與學者們的積極響應。該模型為轉捩模型的二次開發者提供了一個非常優秀的平臺：Medida＆Baeder［57］將方程與航空工程中更常用的S-A相結合；Watanabe等人［58］和Seyfert等人［59］添加了橫流轉捩的經驗關系式；Lin等人［60］添加了更適合發動機吊艙的經驗關系式；Dassler［61］為模擬粗糙對轉捩的影響而添加“粗糙放大因子”的輸運方程。

Seyfert［62］對比了間歇因子轉捩模型與eN方法預測轉捩的結果，表明對于分離導致的轉捩預測γ-Reθ模型表現得非常好，但是如果來流湍流度大于0.1%，那么邊界條件的設置就比較麻煩，而對eN方法來說，來流湍流度只影響經驗參數N。對于簡單的流動來說模型的計算更加耗時，而對于大型三維計算來說模型可能會因使用當地變量的并行計算而更加有效。

國內學者對間歇因子模型也進行了一些研究，例如孫振旭等［63］在渦粘系數輸運方程的基礎上增加了間歇因子方程，他們的方法更接近早期間歇因子模型的理念，即用間歇因子作為層流區與湍流區、邊界層與外部流動過渡的方式，而沒有引入經驗相關公式。張玉倫等［64］對模型中來流湍流度的表達式做了改進，用一個以入口湍流度為變量的顯示表達式取代當地變量的計算獲得自由流動中的湍流度，好處是這樣更方便與實驗結果相對照而不至于引起“來流湍流度”概念的模糊，這實際上是湍流模型本身對轉捩模型運算過程的影響。張曉東等［65］比較了基于SA模型和基于SST模型的轉捩模型之后同樣注意到了這一點：SA模型對帶有激波的流場計算結果準確性下降。同時他們也指出更多的方程計算同樣的流場需要更多的時間，這個問題對于具有3到4個方程的轉捩模型來說尤為突出。

Menter＆Langtry的模型以工程應用為出發點，依靠經驗公式，力求簡單、實用，對轉捩具體機制則不做深究，是這一類模型的典型代表。

3 表征擾動發展的層流脈動模型

用模型方程來計算擾動在層流中發展的過程進而判斷轉捩是轉捩模型的另一種思路。

Lin［66］對自由來流擾動進入邊界層過程進行了深刻的理論分析，認為層流中的脈動主要是通過自由來流中的壓力脈動而不是通過擴散進入邊界層。他用非定常歐拉方程消去邊界層方程中的壓力項，并假設自由來流擾動的頻率滿足ω?υ／δ2的關系，得到層流脈動速度u′的漸近解：

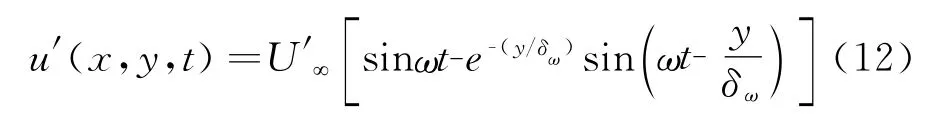
根據Lin的理論，只有當自由來流中的湍流度與流向距離無關的時候，層流脈動才不會產生雷諾應力［67］。當來流湍流度很低的時候，來流脈動在流動方向的衰減不太明顯，層流中雷諾應力可以忽略不計，但是當來流湍流度較高的時候，如6%甚至更大，那么雷諾應力就不能忽略不計了。正如Dyban［68］的結果所展示的那樣，層流邊界層的時間平均速度型受到了明顯的影響。Volino＆Simon［69-70］在實驗中發現，如果來流湍流度較高，早在轉捩開始以前，邊界層內就會出現明顯的雷諾應力。這種現象必然導致層流邊界層的摩擦和熱傳導顯著增強，因此很有必要在數值模擬中加以考慮。

Mayle［67］提出了新的轉捩模型，借用Lin的方法，用非定常歐拉方程消去壓力項，推導出層流動能的輸運方程：

該方程與常見的湍動能方程最大的不同之處在于，“壓力脈動項”為層流動能方程提供了主要的產生項，對應層流中的脈動動能與湍流中的脈動動能不同的產生機制。這樣，就用一個模型方程描述了邊界層擾動的感受過程和發展過程。

關于轉捩的判斷依據，Liepmann［71］提出，當邊界層內雷諾應力與壁面剪切應力相等的時候轉捩即開始。Sharma［72］給出該方法的數學表達式：

Mayle以此為基礎進行了調整，并且測試了來流湍流度1%這樣一個介于自然轉捩和Bypass轉捩之間的算例，結果表明該模型對這種條件有相當好的適應性。

繼Mayle之后，Volino［73］在模型中也考慮了層流中的雷諾應力。Volino將動量方程的粘性系數分成了3個部分：分子粘性、湍流粘性系數和由自由來流引起的渦粘系數，即：

并根據Bradshaw［74］提出的Splat機制，自由來流中的脈動速度v′直接與層流邊界層中的流向脈動速度u′相關，再假設v′與到壁面距離的尺度相同，進而用v′替代混合長模型中的長度尺度，即可得到層流中雷諾應力對應的旋渦粘性系數：

Volino的方法極大地改進了標準的混合長模型。由于這種將層流脈動與湍流脈動產生的渦粘系數分離的方法比較簡單而易于操作，所以也可以很方便地用到其它現有的湍流模型上。

同樣是考慮到分裂機制中脈動速度v′的重要意義，Lien等［75］將k-ε-v2模型［76］應用到了Bypass轉捩的模擬。值得一提的是，該模型沒有使用間歇因子而實現了從層流到湍流的光滑過渡。使用該模型的計算結果表明，在低湍流度下轉捩位置的預測被提前了，并且低估了u′的峰值，出現這種情況的原因可能是源項f在轉捩區間的能量傳遞需要更進一步的調整［］。

Johnson［77］根據先前的直接數值模擬結果［78］，在構建模型的時候也嘗試模擬自由來流中的脈動進入邊界層的過程，發現計算中當來流湍流度較低的時候，也就是積分長度尺度與邊界層厚度相近的時候，轉捩的位置、轉捩區長度與積分長度尺度有明顯的依賴關系，而湍流度越高，這種依賴關系則越不明顯。Jacob［79］的DNS結果表明，自由來流中只有低頻大尺寸旋渦能夠進入邊界層，可能與Johnson的計算結果有一定的聯系。

Walters＆Leylek［80］提出了使用當地變量判斷轉捩的kl-kT-ε三方程模型：

該模型沿用了Mayle＆Schultz關于層流動能的概念，將流動中的脈動動能分成了層流動能kL和湍流動能kT兩個部分，并提出低頻擾動對應的大尺寸旋渦正是在壁面限制下才出現了Splat機制，當遠離壁面或者旋渦尺寸較小的時候不出現Splat機制，進而定義有效長度尺度

根據有效長度尺度，將湍動能分成了小尺度湍動能kT，s和大尺度湍動能kT，l，并且對應地將渦粘系數分成了大尺度粘性系數和小尺度粘性系數，再用大、小尺度粘性系數定義層流動能方程和湍流動能方程的產生項。脈動動能的耗散率也被分成了3個部分

方程中的ε，DT，DL，分別是遠場耗散、由壁面無滑移條件對層流脈動和湍流脈動產生的耗散，在后續的文章中［81］被稱為各項同性耗散與非各向同性耗散。

在能量的輸運項中，使用了3個當地的雷諾數：基于湍動能的雷諾數、基于剪切率的雷諾數d2S／υ和基于層流動能的雷諾數，當這些雷諾數或者其組合形式超過一個臨界值：CBP，crit和CNAT，crit，模型就會激活能量傳遞項，讓層流動能轉化成湍流動能。這樣的判斷方法與先前Menter提出的使用當地量的間歇因子模型判斷轉捩的方式有類似之處。

Walters的模型［80-81］構建之初就試圖表達完整的轉捩過程，尤其是轉捩過程中的能量傳遞，很少有人會對其進行建模。目前沒有看到有文章做更進一步的嘗試。

當然，Walters等人將關注的重點放在了Bypass轉捩之前的脈動變化而沒有進一步考慮模型在計算其它流動現象時的性能，比如分離流動。為此，陳燦平等［82］引入分離敏感參數Cs修正小尺度粘性系數的表達式，增大了模型在分離區的湍流產生能力，進而改進了其在流動分離區域的計算準確性。宋博等［83］用層流動能方程對高超聲速邊界層的轉捩進行了預測，這里的方程形式被假設與不可壓縮流動中一致，但是時間尺度中增加了Mack第二模態。結果表明不可壓縮流動的間歇因子經驗公式并不太適用于可壓縮流動。

4 表征不穩定性模態的不穩定波模型

穩定性理論從波動的角度看待擾動在邊界層內的發展。eN方法計算不穩定波的增長率及放大因子N就是穩定性理論的直接應用［84］。穩定性理論以數學中特征值理論為出發點，經過了大量的研究，并且通過eN方法在實踐中有不少的應用。由于這類計算對條件有很苛刻的要求，復雜流場的適應性不好。對于復雜的轉捩機制，如高超聲速邊界層的轉捩預測，從Su＆Zhou［85］的研究結果來看，需要對傳統的eN方法進行明顯的人為調整才能得到與實驗相符的結果，所以這種方法本身對于工程應用來說就具有一定的難度，還有待進一步發展和完善。

如果能在轉捩模型中使用穩定性理論的成果，則能夠彌補eN方法在實踐中的諸多不足之處。

Wilcox曾指出，k-ω模型中，單位湍動能耗散率的倒數實際上就是一種時間尺度，意味著ω可以表示某一種波動的頻率。根據這種理解，Young［86］提出用不穩定波的長度尺度或頻率來構造層流邊界層中的渦粘系數：

在Young的模型中，使用Mitcheltree［87］的一方程湍流模型計算脈動動能，而使用Walker［88］的經驗公式來計算最不穩定TS波的頻率：

Warren＆Hassan［89-91］沿用了Young表達不穩定波的方法，在Robinson等人［92］的k-ζ模型的基礎上，分別對由TS波與橫流波主導的轉捩流動進行了建模。Warren＆Hassan認為k-ζ模型在模擬湍動能（k）方程與渦擬能（ζ）方程的過程中并沒有刻意強調流動究竟是層流、湍流還是轉捩流動，所以模型方程不需要改動而可以直接用于轉捩流動的計算，僅僅需要修改渦粘系數中的時間尺度即可：

TS波［89］：

橫流波［90］：

Nance［93］在該模型中加入了Mack第二模態時間尺度用以計算高速流動的轉捩：

Mack第二模態：

并進行了實驗驗證［94］。Edwards等人［95-96］將不穩定波的時間尺度加入到層流脈動動能的輸運方程中，形成了渦粘系數的一方程轉捩模型，并用Dhawan＆Narasimha的間歇因子函數與S-A模型作過渡。Song＆Lee［97］在他們之前工作的基礎上，將Farve平均層流動能方程模型化，加入Nance的可壓縮模態時間尺度用以封閉模型，同時模擬了可壓縮流動中特有的壓力功項、壓力擴張項，結果表明該模型在計算高超聲速的邊界層轉捩流動具有不錯的效果。

對于轉捩開始的判斷，Warren＆Hassan的模型及其擴展形式均使用湍流雷諾數RT（認為當RT≥1的時候轉捩發生），很容易讓人聯想到Wilcox用湍流雷諾數RT構造漸近函數的k-ω轉捩模型。有文章發現這種判斷方法對幾何外形具有一定的依賴性［］。

Wang＆Fu［98-102］根據Rumsey［103］的建議（沒有必要將層流脈動和湍流脈動區分并作2個輸運方程來計算），將SST模型中的k作為層流脈動動能與湍流脈動動能之和，并增加了完全使用當地變量的間歇因子輸運方程：

用不穩定波的時間尺度加入到渦粘系數的表達式中以模擬不穩定波的發展過程，同時不失為一種模塊化地改造轉捩模型以適應不同轉捩機制的形式：

第一模態

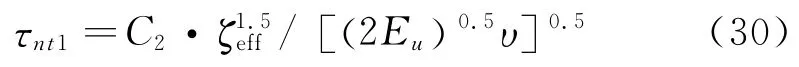
第二模態

橫流模態

轉捩長度尺度

不穩定波時間尺度的構造使用流場中的“當地變量”（相比之下Warren＆Hassan使用的是邊界層的厚度和位移厚度），免除了邊界層積分量的計算，便于在非結構復雜網格上進行計算。轉捩起始的判斷用了形式比較復雜的參數，并以漸近函數的形式出現在間歇因子方程的產生項中，讓輸運方程在迭代中自動完成間歇因子的增長。

Wang＆Fu模型的構建思路用到了多年以來轉捩模型研究諸多的重要成果，無論是方程的組成形式還是其計算轉捩的效果來看都達到了比較完善的程度，應該具有不錯的實用性。Tu等人［104］對Wang＆Fu的模型做了一點改進，用剪切變形率S替換了能量的梯度▽｜Eu｜以減小存儲需求。嘗試計算的結果表明，該模型對從低速到超聲速流動轉捩都能準確地預測。同時Tu指出計算發現間歇因子γ收斂速度較慢，原因可能在于該模型中間歇因子的增長受到間歇因子方程和當地變量k的反饋限制。

到目前為止，穩定性理論成果的應用還比較淺顯，畢竟2種方法區別較大，統一起來存在難度。

5 討 論

前面回顧了4個種類的轉捩模型：只進行簡單修正的低雷諾數湍流模型、根據經驗公式判斷轉捩的間歇因子模型、考慮感受性機制的層流脈動模型、借助穩定性理論的不穩定波模型。不難發現，無論是模型方程的構造方法，還是轉捩預測的實際效果，轉捩模型已經發展進入到比較成熟的階段。那么，現有轉捩模型仍存在那些不足？是否還有進一步發展的空間？多年的發展給我們留下了哪些寶貴的經驗？還需要做進一步的探討。

首先，我們清楚地看到轉捩模型的發展建立在轉捩研究的基礎上，而物理機制和經驗公式是轉捩研究的主要成果。物理機制的研究主要是探討轉捩過程中流場的詳細變化及其原因；經驗公式的建立則是通過分析大量的統計數據，用數學表達式將轉捩起始位置、轉捩區長度等工程中關心的信息與流場條件聯系起來。前者復雜而嚴謹、后者明確而直觀。在轉捩模型中如何取舍這2類研究成果，是在轉捩模型構造之初就必須思考的問題。

若要用模型方程表達物理過程，無外乎出于以下幾點考慮：

（1）借助對轉捩的物理過程進行細致的描述，更加準確地計算轉捩過程中出現的多種流動特性；

（2）參考湍流模型的構造經驗，如果轉捩模型方程能夠接近流動的本質，那么也許可以改進模型對于復雜流動中轉捩計算的準確性；

（3）弱化對經驗公式的依賴，對轉捩的判斷更合理、更有說服力；

（4）隨著轉捩過程物理機制的深入研究，對物理過程建立模型可能要比做大量實驗以獲取經驗公式更快捷；

（5）學術上的追求，大量使用經驗公式這種以“簡單方法解決復雜問題”為指導思想的工程型方法總看起來不夠“完美”。

然而用模型表示轉捩的物理過程并不簡單。完整的轉捩過程包括感受、發展和破碎3個階段，其中發展階段相對簡單，感受和破碎2個階段更加復雜，也是現今轉捩物理機制研究的重點。

自由來流中的旋渦擾動進入邊界層的感受過程被Bradshaw［74］稱為Splat機制，簡單地說就是在壁面的作用下自由來流中的法向脈動進入邊界層之后變成了流向脈動，進而出現“層流脈動動能”。Jacobs＆Durbin［79］發現只有相對較大尺度的脈動才會進入邊界層，于是Walters＆Leylek［80］在其kl-kT-ε模型中，用有效長度尺度分離出這種“長度尺度相對較大的湍流脈動”，并以“大尺度粘性系數”的形式出現在“層流脈動動能”的產生項中。如果將Splat機制中壁面對脈動的“redirection”作用理解成剪切的結果，那么這種建模非常合理，計算結果與實驗結果的吻合也很好。當然，這里有個默認的假設：層流中出現雷諾應力是層流中大尺度湍流脈動的結果。這樣的說法看起來比較矛盾，因為Walters＆Leylek的“層流脈動動能”實際上表示的是一種特定的非各項同性脈動的能量，而“湍流脈動動能”則表示的是另一種非各項同性脈動與各項同性脈動之和的能量。這一點可以從文章中將耗散率拆分成3項看出。反觀Boussinesq渦粘系數的概念，與流動方向垂直的脈動帶來的動量交換才會產生旋渦粘性，所以Walters＆Leylek的處理也是合情合理。

對于高超聲速邊界層來說，在前緣附近，快、慢速聲波與F模態、S模態不穩定波的時間尺度和長度尺度基本一致，所以并不需要復雜的尺度轉換機制即可進入邊界層，但是聲波在飛行器前緣附近可能發生散射、衍射等聲學現象，從而影響前緣對聲波擾動的感受性［6］，這一點似乎還沒有在轉捩模型的研究中有所體現。另外F模態對有旋擾動的感受性取決于沿程雷諾數的現象以及F模態與S模態相互作用而誘發Mack第二模態的過程也沒有被考慮到轉捩模型中。所以目前對高超聲速轉捩模型來說，采用Warran＆Hassan的方法，將Mack第二模態簡化成一個不穩定波的時間尺度帶入層流粘性系數進行運算不失為一個不錯的選擇，這也正是McDaniel等［94］、Song＆Lee［97］、Wang＆Fu［98］所采用的方法。另一個問題是從雷諾平均方程到Favra平均方程所帶來的變化。為了能準確計算Ma＞5的層流動能方程，Song＆Lee［97］增加了顯式的可壓縮效應相關項，并參照對于可壓縮湍流的研究結果對其進行了建模，計算結果表明這樣做確實改進了對轉捩位置預測的準確性。

關于轉捩的破碎階段，Walters＆Leylek根據Andersson的觀察結果，用湍動能、有效長度尺度和分子粘性組成一個當地變量來進行判斷。Walters＆Leylek在文章中坦言，到目前為止，破碎開始的機制并沒有研究清楚，于是只能通過流場中一些具有代表性的無量綱參數構造漸近函數。此前，Mayle的層流動能模型也出現類似的情況。這其實相當于將這些無量綱參數與破碎現象建立了某種經驗公式。這種經驗公式肯定在模型的計算中有不錯的效果，但是并不一定與實際中的數據相符合，有可能僅僅是作為一種數學手段而被創造出來。這其實就與Wilcox的低雷諾數修正沒有本質的區別，只是總體上來說，低雷諾數修正忽略的因素太多而已。

所以，在目前對轉捩認識水平的基礎上，想要用模型來模擬完整的物理機制基本上還是不可能的，還必須要或多或少地依賴經驗公式，甚至需要用到純粹為數值計算而構造出來的關系式。

依賴經驗公式，肯定能解決不少工程問題，但是也有不足之處。

很多情況下，只需要知道轉捩開始的位置，然后做出合理的過度，最后完全使用湍流模型就可以了，這也是基于經驗公式的轉捩模型的一貫做法。有時候，也還需要考慮其它的因素，比如轉捩之前的雷諾應。其實借助經驗公式也可以做到，不穩定波模型［89-91，98-102］本質上就是這樣的例子，只是用穩定性理論幫助建立經驗公式而已。

用經驗公式判斷轉捩，思路上簡單明確，但是在程序中操作起來不是那么簡單，因為經驗公式（如Abu-Ghannam＆Shaw［49］的成果）多數要用到邊界層的宏觀量，如動量厚度這樣的積分量。Menter＆Langtry基于“當地變量”的模型［51-53］革新了經驗公式的使用模式，幾乎徹底解決了這個困難，并且以模塊化的思路設計了轉捩模型。于是，如前面所述，各種新近總結出來的經驗公式立刻被加入到了轉捩模型中。

但是當地變量也會帶來一些新的問題。基于當地化的考慮，Menter＆Langtry用當地湍動能和當地速度計算湍流度，而不是自由來流的湍流度，與通常的經驗關系式有顯著的不同，于是不能使用現有的經驗結果、需要重新建立。另外，正因為當地速度的使用，導致該模型不具有伽利略變換不變性，即臨界動量厚度的計算結果隨參考系選取的不同而發生變化。盡管這個缺陷對于通常的計算情況，即所有壁面都位置固定并與參考系固連時不會有任何影響，但是若有移動壁面的情況則會出現問題［7］。

另外，轉捩模型的一項重要任務是評估轉捩控制方法在工程中的應用效果。常見的層流控制手段，比如吸氣控制，對于二維平板邊界層來說，改變時間平均速度型而改變擾動的增長率，進而抑制擾動增長、延遲或消除轉捩；對于三維平板邊界層而言，均勻排布的孔型吸氣導致邊界層內出現整齊的橫流渦，這些橫流渦的間距決定了流場對邊界層二次不穩定性的抑制情況，進而提前或延遲轉捩［105-106］。用傳統的經驗公式模擬前者比較容易，但是模擬后者的效果恐怕就不那么理想了，因為微觀的物理機制產生了決定性的影響。至于新型的控制方法，如放置在機翼前緣的粗糙單元控制［107-109］、柔性壁控制［110-111］等等，同樣都涉及到更深入的物理機制，單憑經驗公式應該是不夠的，或者說還需要構建新的經驗公式用于幫助解決轉捩模型中遇到的問題。

事實上，即使用穩定性理論預測轉捩也不能回避經驗公式的使用，比如eN方法。近年來，穩定性理論的一些高級方法，比如非線性穩定方程（NPSE）被大量地使用來研究轉捩破碎的機制，例如二次不穩定性的研究［112-113］。如果考慮二次不穩定性，并借用這些方法的結果來做經驗公式，用于判斷破碎的開始可能會更合理、準確，Malik［112］就認為用二次不穩定性作經驗公式比只考慮主模態更可靠。目前，對三維邊界層轉捩中二次不穩定性的產生已經有一些研究結果，不過具體如何進行是值得研究的問題。

6 結 論

將轉捩模型分成了4種類型，分別回顧了的其發展背景和構建思路，并在此基礎上進行了討論。經過多年的發展，轉捩模型的準確性和實用性已經明顯提高，普遍具有以下幾個特點：

（1）借助經驗公式全面考慮環境對轉捩的影響因素；

（2）一定程度上體現轉捩的物理機制；

（3）附加方程以計算額外的轉捩相關變量；

（4）使用“當地變量”進行計算；

（5）模塊化設計、可移植性好。

轉捩模型的發展當然首先應該考慮工程中的實際需求。限于對轉捩機制認識的不足，目前的轉捩模型仍舊不能完整地表達轉捩的物理機制，進而對于涉及到這些機制的層流控制方法不能有效地模擬，所以轉捩模型的發展應與轉捩機制的研究同步進行。常用的經驗公式都是多年以前給出的結果，與目前轉捩模型發展的需求已經不太適應，需要以新的思路來研究轉捩過程的參數變化。最后，轉捩模型的發展還應該以更簡潔、更可靠、更通用為目標，并且兼顧考慮降低對于邊界層網格的依賴性、減少計算量、提高收斂速度等方面的問題，從而更好地體現在工程中的價值。

國內對轉捩模型研究的起步較晚，不過也達到了較高的水平。隨著我國工業水平的逐漸提高，準確預測復雜流動中轉捩位置的計算模型勢必會為高水平的工程設計提供有力的幫助。

［1］Crouch J D.Modeling transition physics for laminar flow control［R］.AIAA 2008-3832

［2］Mayle R E.The 1991 IGTI Scholar Lecture：The role of laminar-turbulent transition in gas turbine engines［J］.ASME J Turbomach，1991，113（4）：509-536.

［3］Yury S Kachanov.Physical mechanisms of laminar-boundary-layer transition［J］.Annu Rev Fluid Mech，1994，2：64，11-82.

［4］Ronald D Joslin.Aircraft laminar flow control［J］.Annu Rev Fluid Mech，1998，30：1-29

［5］Gary Cheng，Robert Nichols，Kshitij D Neroorkar，et al.Validation and assessment of turbulence transition models［R］.AIAA 2009-1141.

［6］Alexander Fedorov.Transition and stability of high-speed boundary layers［J］.Annu Rev Fluid Mech，2011，43：79-95.

［7］Pasquale D Di，Rona A，Garrett SJ.A selective review of CFD transition models［R］.AIAA 2009-3812.

［8］Lardeau S，Li N，Leschziner M A.Large-eddy simulation of transitional bondary layers at high free-stream turbulence intensity and implications for RANS modeling［J］.Journal of Turbomachinery，2007，129：311-317.

［9］Smith A M O，Gamberoni N.Transition pressure gradient and stability theory［M］.Douglas Aircraft Company，Long beach，California，Rep ES 26388，1956.

［10］Van Ingen J L.A suggested semi-empirical method for the calculation of the boundary layer transition region［R］.Univ of Deft Dept Aerospace Engineering，Delft，The Netherlands，Rep VTH-74，1956.

［11］Normann Krimmelbein，Andreas Krumbein.Automatic transition prediction for three dimensional configurations with focus on industrial applications［R］.AIAA 2010-4292.

［12］Spalart P R，Allmaras S R.A one equation turbulence model for aerodynamic flows［R］.AIAA 92-0439.

［13］Jones W P，Launder B E.The calculation of low-Reynolds-number phenomena with a two-equation model of turbulence［J］.International Journal of Heat and Mass Transfer，1973，16：1119-1130.

［14］Wilcox D C.Turbulence modeling for CFD-3rd ediction［M］.DCW Indurstries，Inc.

［15］Launder B E，Reece G J，Rodi W.Progress in the development of a Reynolds-stress turbulence closure［J］.J Fluid Mech，1975，68（3）：573-566.

［16］Menter F R.Zonal two equationk-ωturbulence models for aerodynamic flows［R］.AIAA 93-2906.

［17］Durbin P A.Separated flow computation with thek-ε-v2model［J］.AIAA Journal，1995，33（4）：659-664.

［18］Christopher L Rumsey，Philippe R Spalart.Turbulence model behavior in low Reynolds number regions of aerodynamics flowfields［R］.AIAA 2008-4403.

［19］Wilcox D C.Simulation of transition with a two equation turbulence model［J］.AIAA Journal，1994，32（2）：247-255.

［20］Wilcox D C.Turbulence model transition predictions［J］.AIAA Journal，1975，13（2）：241-243.

［21］Patel V，Yoon J.Application of turbulence models to separated flows over rough surfaces［J］.Journal of Fluids Engineering，1995，117：234-241.

［22］Launder B E，Sharma B A.Application of the energy dissipation model of turbulence to the calculation of flow near a spinning disc［J］.Letters in Heat and Mass Transfer，1974，1：131-138.

［23］Craft T J，Launder B E，Suga K.Prediction of turbulent transitional phenomena with a nonlinear eddy-viscosity model［J］.International Journal of Heatand Fluid Flow，1997，18（1）：15-28.

［24］Chen W L，Lien F S，Leschziner M A.Non-linear eddyviscosity modeling of transitional boundary layers pertinent to turbomachine aerodynamics［J］.Int J Heat Fluid Flow，1998，19：297-306.

［25］Chen W L，Lien F S，Leschziner M A.Computational prediction of flow around highly loaded compressor-cascade blades with non-linear eddy-viscosity models［J］.Int J Heat Fluid Flow，1998，19：307-319.

［26］Savill A M.Evaluating turbulence model predictions of transition［J］.Applied Scientific Research，1993，51：555-562.

［27］符松，王亮.湍流轉捩模式研究進展［J］.力學進展，2007，37（3）：409-416.Fu Song Wang Liang.Progress in turbulence／transition modelling［J］.Advances in Mechanics，2007，37（3）：409-416.

［28］徐星仲，朱斌，蔣洪德.一種新的k方程轉捩湍流模型［J］.工程熱物理學報，1998，19（1）：34-39.Xu Xingzhong，Zhu Bin，Jiang Hongde.A new k-equation turbulence transition model［J］.Journal of Engineering Thermophysics，1998，19（1）：34-39.

［29］錢煒琪，詹浩，白俊強，等.一種基于湍流模式的轉捩預測方法［J］.空氣動力學學報，2006，24（4）：502-507.Qian Weiqi，Zhan Hao，Bai Junqiang，et al.Study of numerical method for flow transition prediction based on turbulence model［J］.Acta Aerodynamica Sinica，2006，24（4）：502-507.

［30］嚴明，宿興遠，魏然，等.應用改進的低雷諾數湍流模型預測轉捩流動［J］.航空動力學報，2009，24（12）：2683-2688.Yan Ming，Su Xingyuan，Wei Ran，et al.Prediction of transitional flows using an improved low-Reynolds-number turbulence model with transition sensitivity［J］.Journal of Aerospace Power，2009，24（12）：2683-2688.

［31］張揚，徐晶磊，白俊強，等.一種基于湍動能方程的轉捩判定方法［J］.力學學報，2014，46（1）：160-164.Zhang Yang，Xu Jinglei，Bai Junqiang，et al.A transition prediction method based on turbulence kinetic equation［J］.Chinese Journal of Theoretical and Applied Mechanics，2014，46（1）：160-164.

［32］肖志祥，陳海昕，李啟兵，等.轉捩模式對轉捩的初步研究［J］.計算物理，2006，23（1）：61-65.Xiao Zhixiang，Chen Haixin，LI Qibing，et al.A primary study of transitions in turbulence models［J］.Chinese Journal of Computational Physics，2006，23（1）：61-65.

［33］Dryden H L.Turbulence and the boundary layer［J］.J Aero Sci，1939，6：85-100.

［34］Emmons H W.The laminar-turbulent transition in a boundary layer-Part I［J］.J Aeronaut Sci，1951，18：490-498.

［35］Schubauer G B，Klebanoff P S.Contributions on the mechanics of boundary layer transition［R］.NACA Tech Note TN 3489，1955.

［36］Dhawan S，Narasimha R.Some properties of boundary layer flow during the transition from laminar to turbulent motion［J］.J Fluid Mech，1958，3（4）：418-436.

［37］Paul A Libby.On the prediction of intermittent turbulent flows［J］.J Fluid Mech，1975，68：273-295.

［38］Paul A Libby.Prediction of the intermittent turbulent wake of a heated cylinder［J］.Phys Fluids，1976，19：494.

［39］Narasimha R.The laminar-turbulent transition zone in the boundary layer［J］.Prog Aerospace Sci，1985，22：29-80.

［40］Cesar Dopazo.On conditioned averages for intermittent turbulent flows［J］.J Fluid Mech，1977，81：433-438.

［41］Chevray R，Tutu N K.Intermittency and preferential transport of heat in a round jet［J］.J Fluid Mech，1978，88：133-160.

［42］Ji Ryong Cho，Myung Kyoon Chung.Ak-ε-γequation turbulence model［J］.J Fluid Mech，1992，237：301-322.

［43］Steelant J，Dick E.Modeling of bypass transition with conditioned Navier-Stokes equations coupled to an intermittency transport equation［J］.International Journal for Numerical Methods in Fluids，1996，23：193-220.

［44］Suzen Y B，Huang P G.Modeling of flow transition using an intermittency transport equation［R］.NASA／CR 1999-209313.

［45］Suzen Y Bora，Huang P G，Lennart S Hultgren，et al.Predictions of separated and transitional boundary layers under lowpressure turbine airfoil conditions using an intermittency transport equations［R］.AIAA 2001-0446.

［46］Savill A M.Some recent progress in the turbulence modeling of bypass transition［J］.Near-Wall Turbulent Flows.edited by R.M.C.So.C.G.Speziale and B.E.Launder，Elsevier Science Publishers，1993：829-848.

［47］Savill A M.Further progress in the turbulence modeling of bypass transition.Engineering Turbulence Modeling and Experiments 2，Elsevier Science Publishers B.V.：583-592.

［48］Gostelow J P，Blunden A R，Walker G J.Effects of freestream turbulence and pressure gradients on boundary layer transition［J］.ASME Journal of Turbomachinary，1994，116：392-404.

［49］Abu-Ghannam B J，Shaw R，Natural transition of Boundary Layers-the effects of turbulence，Pressure Gradient，and flow history［J］.J Mech Eng Sci，1980，22（5）：213-228.

［50］Van Driest E R，Blumer C B.Boundary layer transition：freestream turbulence and pressure gradients effects［J］.AIAA Journal，1963，1（6）：1303-1306.

［51］Menter F R，Esch T，Kubacki S.Transition modelling based on local variables［C］.5th International Symposium on Turbulence Modeling and Measurements，Mallorca，Spain，2002.

［52］Menter F R，Langtry R B，Likki S R，et al.A Correlationbased transition model using local variables Part I-model formulation［C］.Proceedings of ASME Turbo Expo 2004，Vienna，Austria，2004：57-67.

［53］Langtry R B，Menter F R，Likki S R，et al.A correlation-based transition model using local variables Part II-test cases and industrial applications［C］.Proceedings of ASME Turbo Expo 2004，Vienna，Austria，2004：69-79.

［54］Langtry R B，Menter F R.Transition modeling for general CFD application in aeronautics［R］.AIAA 2005-522.

［55］Langtry R B，Menter F R.Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes［J］.AIAA Journal，2009，47（12）：2894-2906.

［56］Menter F R，Langtry R B，Volker S.Transition modeling for general purpose CFD codes［J］.Flow Turbulence Combust，2006，77：277-303.

［57］Shivaji Medida，James D Baeder.Application of the correlationbasedtransition model to the Spalart-Allmaras turbulence model［R］.AIAA 2009-3979

［58］Yuto Watanabe，Takashi Misaka，Shigeru Obayashi.Application of crossflow transition criteria to local correlation-based transition model［R］.AIAA 2009-1145.

［59］Seyfert C，Krumbein A.Correlation-based transition transport modeling for three-dimensional aerodynamic configurations［R］.AIAA 2012-0448.

［60］Lin Y J，Robinson T，Early J，et al.Implementation of Menter’s transition model on an isolated natural laminar flow nacelle［J］.AIAA Journal，2011，49（4）：824-835.

［61］Patrick Dassler，Dragan，Andreas Fiala.Modeling of roughness induced transition using local variables［C］.European Conference on Computational Fluid Dynamics，2010

［62］Seyfert C，Krumbein A.Evaluation of a correlation-based transition model and comparison with the eN method［J］.J Aircraft，2012，49（6）：1765-1773.

［63］孫振旭，趙曉利，宋婧婧，等.關于一個新型轉捩模式的研究與應用［J］.應用數學和力學，2009，30（12）：1463-1472.Sun Zhenxu，Zhao Xiaoli，Song Jingjing，et al.Numerical investigation on a transition prediction model［J］.Applied Mathematics and Mechanics，2009，30（12）：1463-1472.

［64］張玉倫，王光學，孟德虹，等.轉捩模型的標定研究［J］.空氣動力學學報，2011，29（3）：295-301.Zhang Yulun，Wang Guangxue，Meng Dehong，et al.Calibration oftransition model［J］.Acta Aerodynamica Sinica， 2011，29（3）：295-301.

［65］張曉東，高正紅，傅林.基于SA和SST模型對邊界層轉捩預測的比較［J］.航空計算技術，2012，42（5）：51-55.Zhang Xiaodong，Gao Zhenghong，Fu lin.Comparison ofBoundary Layer Transition Prediction Based on SA and SSTγ-model［J］.Aeronautical Computing Technique，2012，42（5）：51-55.

［66］Lin C C.Motion in the boundary layer with a rapidly oscillating external flow［C］.Proc 9th Int Congress Appl Mech Brussels，1957，4：155-167.

［67］Mayle R E，Schulz A.The path to predicting bypass transition［J］.ASME J Turbomach，1997，119：405-411.

［68］Dyban E Epik E，Suprun T T.Characteristics of the laminar boundary layer in the presence of elevated free-stream turbulence［J］.Fluid Mech-Soviet Res，1976，5：30-36.

［69］Volino R J，Simon T W.Transfer functions for turbulence spectra［J］.Unsteady Flows in Aeropropulsion，ASME AD，1994，40：147-155.

［70］Volino R J，Simon T W.Boundary layer transition under high free-stream turbulence and strong acceleration conditions：Part 2—Turbulent Transport Results［J］.ASME Journal of Heat Transfer，1997，119：427-432.

［71］Liepmann H W.Investigations on laminar Boundary-Layer stability and transition on curved boundaries［R］.NACAACR 3H30（NACA-WR-W-107），1943.

［72］Sharma O P，Wells R A，Schlinker R H，et al.Boundary layer development on turbine airfoil suction surfaces［J］.ASME Journal of Engineering for Power，1982，104：698-706.

［73］Volino R J.A new model for free-stream turbulence effects on boundary layers［J］.ASME JTurbomach，1998，120：613

［74］Bradshaw P.Turbulence：the chief outstanding difficulty of our subject［J］.Exp in Fluids，1994，16：203-216.

［75］Lien F S，Kalitzin G，Durbin P A.RANS mdeling for compressible and transitional flows［C］.CTR summer proceedings，1998.

［76］Durbin P A.Separated flow computations with thek-ε-v2model［J］.AIAA Journal，1995，33（4）：659-664.

［77］Mark W Johnson，Ali H Ercan.A physical model for bypass transition［J］.International Journal of Heat and Fluid Flow，1999，20：95-104.

［78］Voke P R，Yang Z.Numerical studies of the mechanisms of bypass transition in the flat plate boundary layer［C］.Proceedings of 9th Symposium on Turbulent Shear Flows，Kyoto，Japan，1993.

［79］Jacobs R G，Durbin P A.Simulations of bypass transition［J］.J Fluid Mech，2001，428：185-212.

［80］Walters D K，Leylek J H.A new model for boundary layer transition using a single-point RANS approach［C］／／ASME J Turbomach，2004，126：193-202.

［81］Walters D Keith，Cokljat D.A three-equation eddy-viscosity model for Reynolds-averaged Navier-Stokes simulations of transitional flow［J］.ASME J Turbomach，2008，130（12）：121401.

［82］陳燦平，趙慶軍，孫小磊.層流動能轉捩模型改進方法研究［J］.工程熱物理學報，2013，34（8）：1424-1428.Chen Canping，Zhao Qingjun，Sun Xiaolei.Investigation on a improved laminar kinetic energy transition model［J］.Journal of Engineering Thermophysics，2013，34（8）：1424-1428.

［83］宋博，李椿萱.基于非湍流脈動動能方程的高超聲速轉捩預測［J］.北京航空航天大學學報，2013，36（2）：244-247.Song Bo，Lee Chunhian.Laminar-to-turbulent transition onset prediction of hypersonic flows based on laminar kinetic energy equation［J］.Journal of Beijing University of Aeronautics and Astronautics，2010，36（2）：244-247.

［84］Crouch J D，Ng L L.Variable N-factor method for transition prediction in three dimensional boundary layers［J］.AIAA Journal，2000，38（2）：211-216.

［85］Su Caihong，Zhou Heng.Transition prediction of a hypersonic boundary layer over a cone at small angle of attack-with the improvement of eN method［J］.Sci China Ser G-Phys Mech Astron，2009，52（1）：115-123.

［86］Young T W，Warren E S，Harris J E，et al.New approach for the calculation of transitional flows［J］.AIAA Journal，1993，31（4）：629-636.

［87］Mitcheltree R A，Salas M D，Hassan H A.One-equation turbulence model for transonic airfoil flows［J］.AIAA Journal，1990，28（29）：1625-1632.

［88］Walker G J.Transitional flow on axial turbomachine blading［R］.AIAA 87-0010.

［89］Warren E S，Hassan H A.A transition model for swept wing flows［R］.AIAA 97-2245.

［90］Warren E S，Hassan H A.An alternative to the eN method for determining onset of transition［J］.AIAA 97-0825，1997.

［91］Warren E S，Hassan H A.Transition closure model for predicting transition onset［J］.J Aircraft，1998，35（5）：769-775.

［92］Robinson D F，Harris J E，Hassan H A.Unified turbulence closure model for axisymmetric and planar free shear flows［J］.AIAA Journal，1995，33（12）：2325-2331.

［93］Robert P Nance，Thomas J Horvath，Hassan H A.Transition and turbulence modeling for blunt-body wake flows［R］.AIAA 97-2570.

［94］McDaniel R D，Nance R P，Hassan H A.Transition onset prediction for high-speed flow［J］.J Spacecraft＆Rockets，2000，37（3）：304-309.

［95］Edwards J R，Roy C J，Blottner F G，et al.Development of one equation transition／turbulence models［R］.AIAA 2000-0133.

［96］Malechuk A M，Edwards J R，Hassan H A.Simulation of transitional flow over a elliptic cone at Mach 8 using a one equation transition／turbulence model［R］.AIAA 2003-1132.

［97］Song Bo，Lee Chun Hian.A Favre averaged transition prediction model for hypersonic flows［J］.Sci China Tech Sci，2010，53（8）：768-774.

［98］Wang Liang，Fu Song.Modelling flow transition in a hypersonic boundary layer with Reynolds-averaged Navier-Stokes approach［J］.Sci China Ser G-Phys Mech Astron，2009，52（5）：768-774.

［99］Song Fu，Liang Wang，Angelo Carnarius，et al.Modeling supersonic and hypersonic flow transition over three-dimensional bodies［C］.Seventh IUTAM Symposium on Laminar-Turbulent Transition IUTAM Bookseries，2010：493-496.

［100］Wang L，Song Fu.Development of an intermittency equation for the modeling of the supersonic／hypersonic boundary layer flow transition［J］.Flow Turbulence Combust，2011，87：165-187.

［101］Liang Wang，Song Fu，Angelo Carnarius，et al.A modular RANS approach for modelling laminar-turbulent transition in turbomachinery flows［J］.International Journal of Heat and Fluid Flow，2012，34：62-69.

［102］Fu S，Wang L.RANS modeling of high-speed aerodynamic flow transition with consideration of stability［J］.Progress in Aerospace Sciences，2013，58：36-59.

［103］Rumsey C L，Thacker W D，Gatski T B，et al.Analysis of transition sensitized turbulent transport equations［R］.AIAA 2005-0523.

［104］Tu Guohua，Deng Xiaogang，Mao Meiliang.Validation of a RANS transition model using a high-order weighted compact nonlinear scheme［J］.Sci China-Phys Mech Astron，2013，56（4）：805-811.

［105］Ralf Messing，Markus J Kloker.Investigation of suction for laminar flow control of three-dimensional boundary layers［J］.Journal of Fluid Mechanics，2010，658：117-147.

［106］Tillmann Friederich，Markus J Kloker.Control of the secondary cross-flow instability using localized suction［J］.Journal of Fluid Mechanics，2012，706：470-495.

［107］William S Saric，Ruben B Carrillo Jr.，Mark S Reibert.Leading-edge roughness as a transition control mechanism［R］.AIAA 1998.

［108］Radeztsky R H，Reibert M S，Saric W S.Effect of isolated micron-sized roughness on transition in swept-wing flows［J］.AIAA Journal，1999，37（11）：1370-1377.

［109］White E B，Saric W S.Application of variable leading-edge roughness for transition control.on swept wings［R］.Al AA 2000-0283.

［110］Carpenter P W.The optimization of mutiple-panel compliant walls for transition delay［J］.AIAA Journal，1993，31（7）：1187-1188.

［111］Carpenter P W，Lucey A D.Progress on the use of compliant walls for laminar-flow control［J］.Journal of Aircraft，2001，38（3）：504-512.

［112］Mujeeb R Malik，Fei Li，Meelan M Choudhari，et al.Secondary instability of cross-flow vortices and swept wing boundary layer transition［J］.Journal of Fluid Mechanics，1999，399：85-115.

［113］Werner Koch.On the spatio-temporal stability of primary and secondary cross-flow vortices in a three dimensional boundary layer［J］.Journal of Fluid Mechanics，2002，456：85-111.

Review of transition prediction methods

Zhang Wen，Liu Peiqing，Guo Hao，Qu Qiulin
（Beihang University，Beijing 100191，China）

Laminar-turbulent transition can greatly affect the characteristics of boundary layer flow like skin friction and heat transfer.Predicting transition accurately is of great importance in engineering design.The prediction of transition using transition models which develop quickly during past years is very appropriate in engineering applications.Transition models are divided into four types and each type is reviewed in detail respectively.Conclusions are made based on analysis and discussion about the achievements as well as the drawbacks of transition models nowadays，and some suggestions are proposed for transition research and modeling in the future.

laminar-turbulent transition；transition modeling；engineering computation；low Reynolds number；intermittency；laminar fluctuation；instability wave

O357.5

：A

1672-9897（2014）06-0001-13doi：10.11729／syltlx20140030

（編輯：李金勇）

2014-03-10；

：2014-06-04

劉沛清，E-mail：lpq＠buaa.edu.cn

ZhangW，LluPQ，GuoH，etal.Reviewoftransitionpredictionmethods.JournalofExperimentsinFluidMechanics，2014，28（6）：

1-12，38.張 雯，劉沛清，郭 昊，等.湍流轉捩工程預報方法研究進展綜述.實驗流體力學，2014，28（6）：1-12，38.

張 雯（1989-），安徽合肥人，博士研究生。研究方向：邊界層轉捩。通訊地址：北京航空航天大學流體力學研究所（100191）。E-mail：zhangwen＠ase.buaa.edu.cn