基爾霍夫電流定律(KCL)在《電工學》集成運放課程教學中的應用
周遠明,梅 菲,劉凌云,徐進霞,劉曉靜
(湖北工業大學 電氣與電子工程學院,湖北 武漢 430068)
基爾霍夫電流定律(KCL)在《電工學》集成運放課程教學中的應用
周遠明,梅 菲,劉凌云,徐進霞,劉曉靜
(湖北工業大學 電氣與電子工程學院,湖北 武漢 430068)
從基爾霍夫電流定律(KCL)出發,分析了反相比例、同相比例、加法、減法等四種由集成運放組成的運算電路,該方法具有簡單可行、可操作性強等優點,可以提高課堂教學效果和學生的學習興趣,調動學生的主觀能動性,學生評價較好。
基爾霍夫電流定律;電工學;集成運放
電工學是一門非電專業的技術基礎課程,其基本內容是電工技術和電子技術,主要任務是為學生學習專業知識和從事工程技術工作打好基礎,并使他們受到必要的基本技能的訓練。集成運算放大器(簡稱集成運放)是模擬電子技術中的重要器件,是幾乎目前所有的電子設備中都要用到的基本器件。集成運放是電工學中的重點知識,且種類繁多,從而對課堂教學提出了較高的要求。本文結合電工學課程教學實踐,探討基爾霍夫電流定律(簡稱KCL)在集成運放課程教學中的應用。
一、集成運放
運算放大器(簡稱運放)是一種直流耦合、差模(差動模式)輸入、通常為單端輸出的高增益電壓放大器,因為剛開始主要用于加法、減法等模擬運算電路中,因而得名。集成運算放大器(簡稱集成運放)是用集成電路工藝制成的運算放大器,與分立元件組成的放大電路相比,集成運放具有體積小、質量輕、功耗低、工作可靠、安裝方便、價格便宜等眾多優勢,因而在模擬運算、信號處理等領域都有著廣泛的用途。虛短、虛斷是模擬電路中理想集成運放的兩個重要概念。集成運放工作在線性區時,由于運放的開環電壓放大倍數很大,運放的差模輸入電壓通常不足1mV,可以認為兩個輸入端的電位相等u+=u-,即反相與同相輸入端之間相當于短路,但事實上并沒有短路,稱為“虛短”;由于運放的差模輸入電阻很大,一般集成運放的輸入電阻都在1MΩ以上,因此流入運放輸入端的電流往往不足1uA,遠小于輸入端外電路的電流,故通常認為反相與同相輸入端之間相當于斷路,i+=i-≈0,但事實上并沒有斷路,稱為“虛斷”。
二、基爾霍夫電流定律
基爾霍夫定律概括了電路中電流和電壓分別遵循的基本規律,是分析和計算電路的基本依據。基爾霍夫電流定律(簡稱KCL)是用來確定連接在同一結點上的各支路電流間關系的。由于電流的連續性,電路中任何一點(包括結點在內)均不能堆積電荷。因此,在任一瞬間,流入某一結點的電流之和應該等于由該結點流出的電流之和。
三、利用基爾霍夫電流定律分析運算電路
本論文基于秦曾煌主編的第七版《電工學》教材[1],從基爾霍夫電流定律(KCL)出發,分析了反相比例、同相比例、加法、減法等四種由集成運放組成的運算電路,均采用相同的電路分析步驟:(1)應用KCL和虛斷條件i+=i-≈0列結點電流方程;(2)應用歐姆定律將電流方程轉換成電壓方程;(3)應用虛短條件u+=u-簡化電壓方程;(4)得到輸出電壓uO和輸入電壓u1二者之間的關系。
(一)反相比例運算電路
反相比例運算電路如圖1所示,輸入信號u1經輸入端電阻R1接到反相輸入端,而同相輸入端通過電阻R2接地,反饋電阻RF連接在輸出端和反相輸入端之間。
根據i+=i-≈0,可以得到結點a處的電流關系:iI=iF,根據歐姆定律可以得到:
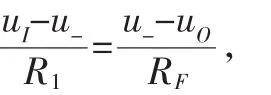
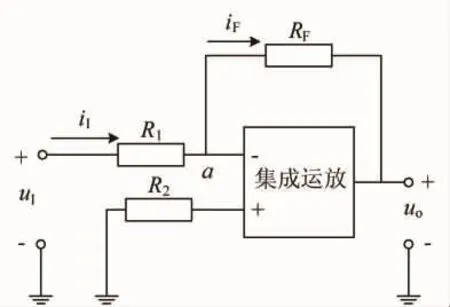
圖1 反相比例運算電路
上式中除了輸入電壓uI和輸出電壓uO之外,還有一個未知量u-,根據u-=u+=-i+R2=0,可以將上式簡化為:
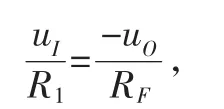
即可得到輸出電壓uO和輸入電壓uI二者之間的關系:
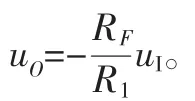
(二)同相比例運算電路
同相比例運算電路如圖2所示,輸入信號uI經電阻R2接到同相輸入端u+,而反相輸入端通過輸入端電阻R1接地,反饋電阻RF連接在輸出端和反相輸入端之間。
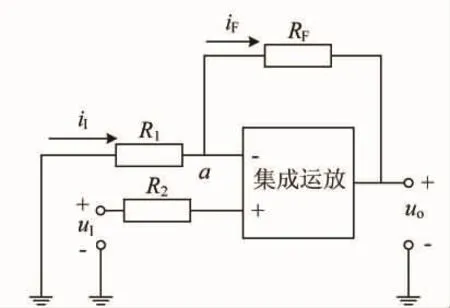
圖2 同相比例運算電路
根據i+=i-≈0,可以得到結點a處的電流關系:iI=iF,根據歐姆定律可以得到:
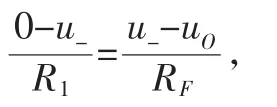
上式中除了輸出電壓uO之外,還有一個未知量u-,根據u-=u+=uI-i+R2=uI,可以將上式簡化為:
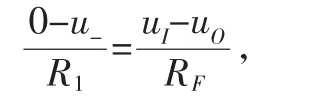
即可得到輸出電壓uO和輸入電壓uI二者之間的關系:
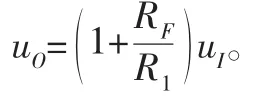
(三)加法運算電路
反相加法運算電路如圖3所示,輸入信號uI1、uI2分別經輸入端電阻R11、R12接到反相輸入端,而同相輸入端通過R2接地,反饋電阻RF連接在輸出端和反相輸入端之間。
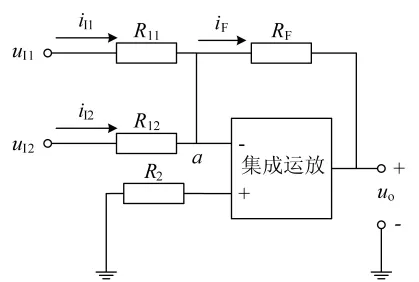
圖3 加法運算電路
根據i+=i-≈0,可以得到結點a處的電流關系:iI1+iI2=iF,根據歐姆定律可以得到:
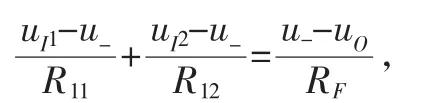
上式中除了輸入電壓uI1、uI2和輸出電壓uO之外,還有一個未知量u-,根據u-=u+=-i+R2=0,可以將上式簡化為:
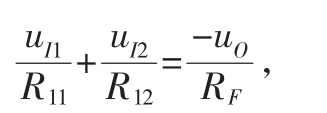
即可得到輸出電壓uO和輸入電壓uI1、uI2二者之間的關系:
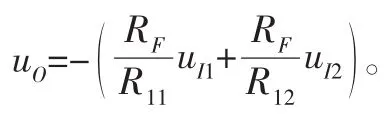
(四)減法運算電路
減法運算電路如圖4所示,輸入信號uI1經輸入端電阻R1接到反相輸入端,uI2經電阻R2、R3接到同相輸入端,反饋電阻RF連接在輸出端和反相輸入端之間。
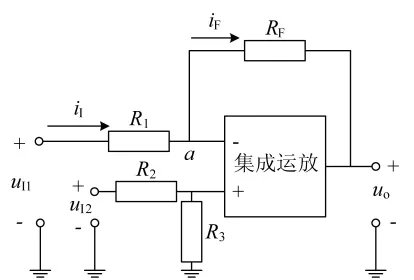
圖4 減法運算電路
根據i+=i-≈0,可以得到結點a處的電流關系:iI=iF,根據歐姆定律可以得到:
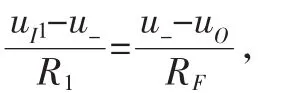
上式中除了輸入電壓uI1和輸出電壓uO之外,還有一個未知量u-,u-和uI2之間滿足關系:
即可得到輸出電壓uO和輸入電壓uI1、uI2二者之間的關系:
四、結論
綜上所述,本文從基爾霍夫電流定律(KCL)出發,分析了反相比例、同相比例、加法、減法等四種由集成運放組成的運算電路,該方法具有簡單可行、可操作性強等優點。此外,KCL還可以應用在基本放大電路的動態分析中,例如輸入、輸出電阻。實踐證明,該方法可以提高課堂教學效果和學生的學習興趣,調動學生的主觀能動性,學生評價較好。
[1]秦曾煌.電工學[M].第七版.北京:高等教育出版社,2011.
G642.41
A
1674-9324(2014)36-0084-02
湖北工業大學教學研究項目(2007005)。
周遠明(1984-),男,湖北仙桃人,博士,講師,研究方向:半導體材料與器件。

