由一道數(shù)學行程問題引發(fā)的思考
——淺談數(shù)學習題的功能
馬鴻曉
(北京市海淀區(qū)北大附中香山學校,北京 100093)
由一道數(shù)學行程問題引發(fā)的思考
——淺談數(shù)學習題的功能
馬鴻曉
(北京市海淀區(qū)北大附中香山學校,北京 100093)
數(shù)學習題的練習在數(shù)學學習中具有重要功能——知識功能和教育功能。教師選擇每一道數(shù)學習題,都應(yīng)該考慮到它的兩種功能,不僅僅教給學生知識,同時還注重學生思維發(fā)展和心理健康成長。可怎樣發(fā)揮這些功能?值得我們深思和探討。
數(shù)學;習題功能;行程問題
數(shù)學習題練習是中學數(shù)學教學過程中的重要一環(huán)。數(shù)學習題具有兩種功能:第一,它是數(shù)學知識的載體,習題練習可以鞏固知識、靈活運用知識、并引入新知識。第二,數(shù)學習題還具有重要的教育功能,它能培養(yǎng)學習興趣、增強學習信心,養(yǎng)成良好數(shù)學學習習慣和學習思維,提高學生應(yīng)對挫折的能力。
下面是一道數(shù)學行程問題的教學片斷,借用該教學片斷來探討如何發(fā)揮數(shù)學習題的這些功能。
一、數(shù)學行程問題教學片段
(一)例題
甲、乙兩車相距480km,甲車速度為80km/h,乙車速度為100km/h,若甲、乙兩車同時同向而行,兩車何時相距600km?
解:設(shè)x小時后兩車相距600km。
1.若甲、乙兩車同向由甲到乙方向行駛,如下頁圖1所示,則:
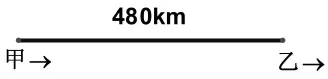
圖1
100x+480=80x+600
解之得:x=6
即:6小時后甲、乙兩車相距600km。
2.若甲、乙兩車同向且由乙到甲方向行駛,如圖2所示,則只有乙追上甲并超過甲時才可能相距600km

圖2
100x=80x+480+600
解之得:x=54
即:54小時后甲、乙兩車相距600km。
(二)拓展
若上述數(shù)據(jù)都不變,設(shè)計一道題,使之結(jié)果有三種情形。
學生:編不出來,能否改變數(shù)據(jù)?
老師:如果可以改變數(shù)據(jù),你如何設(shè)計?
學生甲:將“甲、乙兩車相距480km”更改為“甲、乙兩車同在一個地方”,則:
(1)甲、乙同時同地同向右出發(fā)(如圖3)。
(2)甲、乙同時同地同向左出發(fā)(如圖4)。
(3)甲、乙同時同地反向出發(fā)(如圖5)。

圖3

圖4

圖5
學生乙質(zhì)疑:(1)、(2)屬同一種情況。(其他學生都贊同)
學生丙:將“甲、乙兩車相距480km”更改為“甲、乙兩車相距650km”,刪去“甲、乙兩車同時同向而行“,則:
(1)甲、乙同時相向而行(如圖6)。
(2)甲、乙同時同向出發(fā),此時不可能出現(xiàn)同時向由甲到乙的方向行駛(甲比乙慢,由甲到乙方向行駛,只會導致相距距離越來越大)。
①乙追上甲之前相距600km(如圖7)。
②乙追上甲之后相距600km(如圖7)。

圖6

圖7
學生丁質(zhì)疑:(1)情況下應(yīng)該也有兩種可能性:甲、乙相遇前相距480km;甲、乙相遇后相距480km。
學生丙:將“甲、乙兩車相距480km,甲車速度為80km/h,乙車速度為100km/h”更改為“甲、乙兩車相距600km,甲車速度為100km/h,乙車速度為100km/h”
學生群體質(zhì)疑:甲、乙兩車只要同時同向行駛,永遠相距600km,沒有太多意義。
最后此拓展題只得以“課下再思考”而結(jié)束。
二、從行程問題知識本身的角度反思
此題如果不更改任何數(shù)據(jù),能否設(shè)計出有三種情形的一道題?
行程問題一般涉及三個變量:速度、時間、路程,三個變量相互作用、相互影響。若行程問題只涉及到一個對象,當確定其中兩個變量時,第三個變量隨之可以確定。若行程問題涉及到兩個對象或兩個以上對象(比如:此例題中出現(xiàn)了甲、乙兩個對象),除了三個變量外一般還涉及到兩個對象的行駛方向,以及是否同時行駛兩個要素。對于同時與否,其實質(zhì)為改變兩車之間最初的距離,而方向一般會涉及八種情況(見表1)。
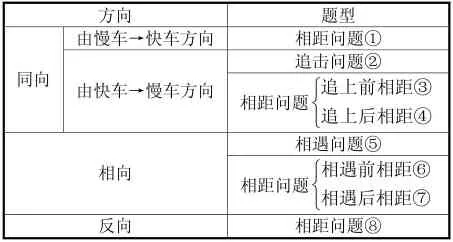
表1
本題中甲乙兩車速度不變,最終要相距600km,屬于相距問題。
1.若兩車最開始相距0<S<600km,則只可能出現(xiàn)表中的①、④、⑦、⑧四種情況。
2.若兩車最開始相距S>600km,則只可能出現(xiàn)表中的③、④、⑥、⑦四種情況。
3.特殊情況之一:兩車在同一地點即S=0km,此時只可能出現(xiàn)同向相距或反向相距兩種情況。
4.特殊情況之二:兩車最開始相距600km即S=600km,此時只可能出現(xiàn)表中的④、⑦兩種情況。
綜上所述,無論從“方向”還是從“同時與否”這兩個角度思考,最終都會出現(xiàn)四種情況或兩種情況,不可能出現(xiàn)三種情況。
三、從數(shù)學習題的教育功能方面來看
數(shù)學習題對學生的智力方面和非智力方面都有重要的功能。
從智力方面來說,數(shù)學習題能培養(yǎng)學生思維的靈活性、敏捷性、深刻性、批判性、廣闊性、創(chuàng)造性等品質(zhì)。本題是一道開放性習題,由于答案的不確定性,不能按照常規(guī)的思路解決問題,要求學生從整體看行程問題,全局把握條件和結(jié)論之間的關(guān)系,在學生已有的解題方法、運算技巧和探索能力的基礎(chǔ)上,擺脫局部細節(jié),主動、獨立、別出心裁的提出新方法、新見解,同時對自己提出的新方法、新見解提出質(zhì)疑,發(fā)現(xiàn)問題,從而擯棄錯誤,尋找出最后的解決方案。所以,此題對學生思維的品質(zhì)提出了很高的要求,能促進學生的思維縱向深層次發(fā)展。
從非智力方面來說,經(jīng)拓展后的習題難度系數(shù)較大,要求學生頑強的、堅持不懈地挑戰(zhàn)已有知識和能力的極限,能培養(yǎng)學生的堅韌和挑戰(zhàn)精神。但學生無論付出多少努力最終也無法成功找到解決方案,會讓學生產(chǎn)生挫折感,習題本身具有的激勵作用也蕩然無存,長此以往,學生就會對具有挑戰(zhàn)性的習題失去興趣和動力。如果我們把這道拓展題的結(jié)論稍作修改,結(jié)果就會大相徑庭。比如:我們將問題“若上述數(shù)據(jù)都不變,設(shè)計一道題,使之結(jié)果有三種情形。”更改為“若上述數(shù)據(jù)都不變,我們能否設(shè)計一道題,使之結(jié)果有三種情形?如果能,請寫出來。如果不能,請找出原因”,此時學生可從“存在”和“不存在”兩方面思考問題。除此以外,我們還可以將問題更改為“若上述數(shù)據(jù)都不變,設(shè)計一道題,使之結(jié)果有四種情形。”,學生因此也能獲得成功,但相比前者,后者對學生的數(shù)學思維能力的要求就降低了許多。
此外,由于數(shù)學習題本身具有的獨特特點,使之較其他學科抗干擾的能力強,學生容易靜下心來,迅速投入到數(shù)學習題解決的過程中去,對于促進學生良好的學習習慣有重要的作用。數(shù)學習題不僅能促進學生獨立思考,還能促進學生養(yǎng)成良好的思維習慣和敢于質(zhì)疑的習慣。
問題是數(shù)學的心臟,問題解決是數(shù)學教育的核心。數(shù)學習題不僅能鞏固學生所學知識,發(fā)展學生的智力,同時對學生情感、心理等方面都有很大的影響。此外,數(shù)學習題還深刻影響著學生進入社會后分析身邊問題、解決身邊問題的能力。所以我們需要慎重地看待每一道數(shù)學習題,認真地思考數(shù)學習題的教育功能,在有限的課堂時間里最大限度地發(fā)揮每一道習題的教育功能。
G633.6
A
1674-9324(2014)36-0082-03
馬鴻曉,北大附中香山學校數(shù)學教師,中學一級教師,海淀區(qū)數(shù)學學科帶頭人。

