基于序列輸入的神經網絡模型算法及應用

肖紅，李盼池

東北石油大學計算機與信息技術學院，黑龍江大慶 163318

基于序列輸入的神經網絡模型算法及應用

肖紅，李盼池

東北石油大學計算機與信息技術學院，黑龍江大慶 163318

為提高神經網絡的逼近能力，提出一種基于序列輸入的神經網絡模型及算法。模型隱層為序列神經元，輸出層為普通神經元。輸入為多維離散序列，輸出為普通實值向量。先將各維離散輸入序列值按序逐點加權映射，再將這些映射結果加權聚合之后映射為隱層序列神經元的輸出，最后計算網絡輸出。采用Levenberg-Marquardt算法設計了該模型學習算法。仿真結果表明，當輸入節點和序列長度比較接近時，模型的逼近能力明顯優于普通神經網絡。

神經網絡；序列神經元；序列神經網絡；算法設計

1 引言

在實際生物神經系統的信息處理過程中，記憶和輸出不僅依賴于每種輸入信息的空間聚合，而且也依賴于輸入在時間上的累積效果[1]。傳統人工神經網絡（Artificial Neural Networks，ANN）較好地模擬了生物神經元的空間聚合、激勵、閾值等特性，但缺乏對時間延遲以及時間累積效果的描述。反映在實際應用中，ANN一次只能接收一個幾何點式的向量輸入，而不能直接接收體現時間累積效果的矩陣式輸入。對于一個矩陣式的序列樣本，ANN通常將其中每個列向量看作單個樣本分多次接收，這種方法由于不能充分利用序列的整體特征，因此逼近能力受到影響。

在很多實際問題中，系統的輸入通常為一個多維的離散序列，在數學上可用一個矩陣表示，例如股票的波動過程、化學反應中溶液濃度的變化過程等。用神經網絡方法研究離散序列輸入系統的建模和仿真逐漸成為智能計算領域的研究熱點。目前的處理方法主要集中在與其他方法的融合和對網絡模型的改進方面。例如，文獻[2-3]利用濾波器能夠消除數據噪聲的優點，將前饋神經網絡與非線性濾波方法相結合，分別采用擴展卡爾曼濾波和無跡卡爾曼濾波訓練網絡，并比較了二者的性能。文獻[4]提出了改進的小波神經網絡模型，通過在隱含層使用不同類型的小波函數作為激勵函數，較大程度地提高了網絡的預測能力。文獻[5]通過在標準小波神經網絡中增加一個中間層，并使該層輸出作為輸出層權值，來提高普通小波神經網的預測性能。針對自回歸整合滑動平均（autoregressive integrated moving average，ARIMA）技術只能處理線性問題，而神經網絡具有較強的非線性逼近能力，文獻[6]提出了一種融合ARIMA的混合神經網絡模型，應用效果表明混合模型明顯優于原模型。文獻[7]采用非線性時變進化的粒子群優化算法動態優化徑向基函數網絡的結構及參數，結果表明該方法使預測精度有明顯的提高。文獻[8]提出一種基于五層神經網絡的遞歸預測方法，其中三個隱含層均采用雙曲正切函數作為激勵函數，為提高收斂速度，采用L-M （Levenberg-M arquardt）方法訓練網絡參數。網絡訓練之后，通過將輸出反饋到輸入端，可以實現遞歸式的連續預測。文獻[9-12]提出了過程神經網絡（Process Neural Networks，PNN）模型，文獻[13-15]提出了基于正交基展開的PNN算法，目前PNN模型在連續逼近及預測方面已經獲得一些成功應用，但由于該模型各維輸入均為連續函數，因此不便于直接處理離散逼近及預測問題。

為了充分模擬生物神經元的時間累積效果，以便提高傳統神經網絡的逼近能力，本文提出一種基于序列輸入的神經網絡模型（Sequence Input-based Neural Networks，SINN），該模型的每個輸入樣本為多維離散序列，可表述為一個矩陣。基于L-M算法設計了該模型的學習算法。以太陽黑子數年均值預測為例，仿真結果表明，當輸入節點數和序列長度比較接近時，該模型的逼近和預測能力明顯優于普通神經網絡。

2 基于序列輸入的神經網絡模型

2.1 基于序列輸入的神經元模型

對于n×q矩陣式樣本，普通神經元將每一列視為單個樣本，而將整個矩陣視為q個n維樣本。為實現對矩陣式樣本的整體映射，本文提出序列神經元模型，如圖1所示。

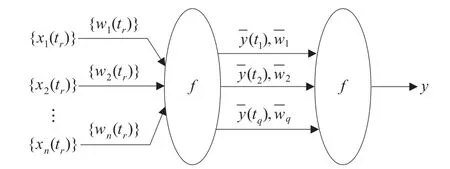
圖1 序列神經元實際模型

圖中{xi(tr)}=[xi(t1)，xi(t2)，…，xi(tq)]，{wi(tr)}=[wi(t1)，wi(t2)，…，wi(tq)]，i=1，2，…，n。f為sigmoid函數。該模型可簡化為圖2。

根據圖1，序列神經元模型輸入輸出關系可按下式計算。

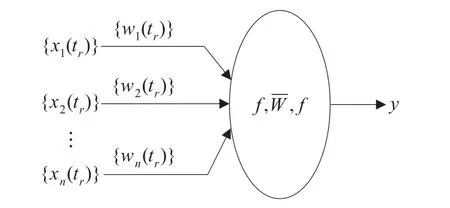
圖2 序列神經元簡化模型

2.2 基于序列輸入的神經網絡模型

本文提出的序列輸入神經網絡模型為三層結構，隱層為序列神經元，輸出層為普通神經元，如圖3所示，圖中g為sigmoid函數。

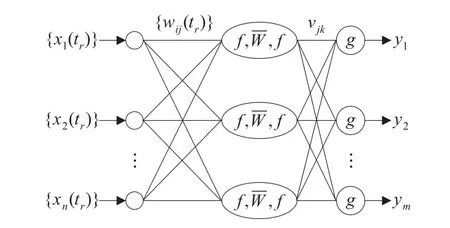
圖3 基于序列輸入的神經網絡模型

3 基于序列輸入的神經網絡算法

3.1 算法原理

令輸入層n個節點，隱層p個節點，輸出層m個節點。給定L個學習樣本，其中第l(l=1，2，…，L)個樣本可表示為：

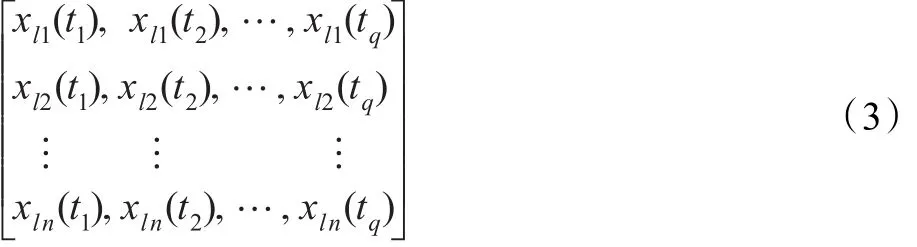
對應輸出樣本為dl1，dl2，…，dlm。

根據序列神經元的輸出式（2），第l個樣本的隱層輸出計算式為：

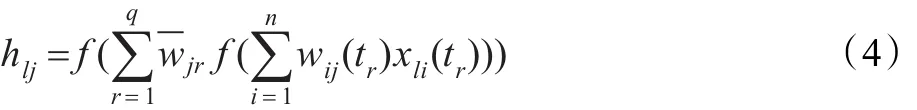
輸出層輸出計算式為：

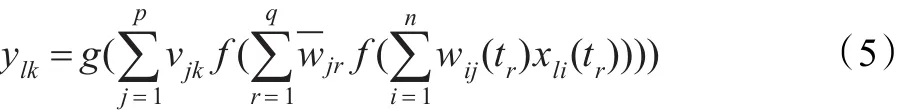
令elk=dlk-ylk，根據梯度下降法，網絡權值調整的梯度計算式為：

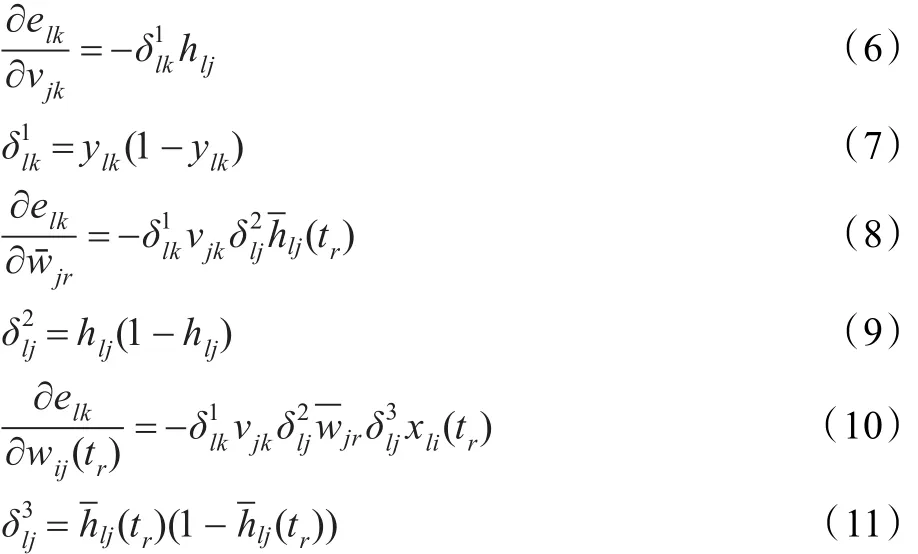
令權值向量為：

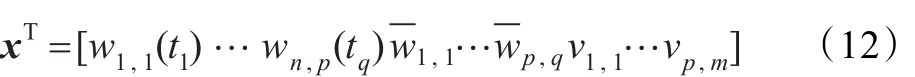
誤差向量為：

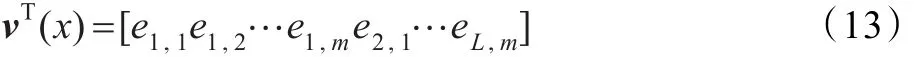
構成的雅可比矩陣為：

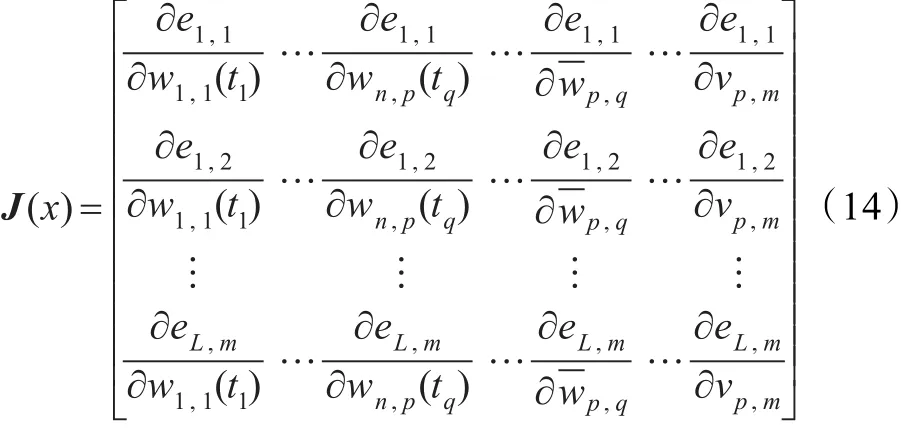
根據L-M算法，網絡權值的調整規則為：

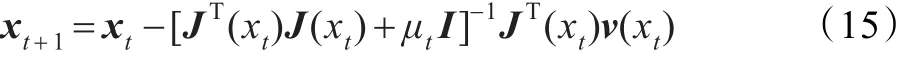
其中t為迭代步數，I為單位矩陣，μt為一小正數，以使JT(xt)J(xt)+μtI可逆。

為便于描述算法終止條件，稱下式定義的Emax為網絡的逼近誤差。

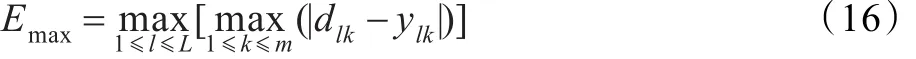
其中m為輸出維數，L為樣本總數。

若逼近誤差小于等于預先設定的限定誤差，或迭代步數帶到預先設定的最大步數，則算法終止。

3.2 實施方案

步驟1模型初始化。包括：序列長度、各層節點數，各層權值的迭代初值，限定誤差E，限定步數G。置當前代數g=1。

步驟2按式（5）計算各層輸出，按式（15）調整網絡權值。

步驟3按式（16）計算逼近誤差Emax，若Emax＞E或g＜G，則g=g+1轉步驟2，否則轉步驟4。

步驟4保存各層權值，停機。

4 仿真對比

4.1 M ackey-G lass時間序列逼近

本節以M ackey-G lass數據逼近作為仿真對象，并與普通三層ANN對比，驗證SINN的優越性。M ackey-Glass序列樣本可由下式產生。

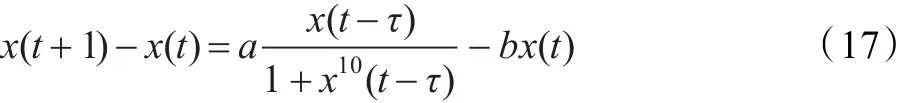
其中t是整數，x(0)∈(0，1)，a=0.2，b=0.1，τ=17。

為使對比公平，兩種算法采用相同的網絡結構，且均采用L-M算法調整權值。由上式生成序列，仿真方案為用前面的m個數據，預測緊鄰其后的1個（即第m+1個）數據。因此兩種模型的輸出層均只有一個節點。為使對比充分，兩種模型隱層均取5，10，…，20個節點。樣本歸一化后的限定誤差取0.05，限定步數取100。兩種模型的初始權值均在(-1，1)中隨機選取，L-M算法的控制參數μt=0.05。ANN隱層和輸出層采用Sigmoid函數。

根據仿真方案，取預測長度m=24。令SINN輸入節點為n，序列長度為q，顯然，q反映在時間上的積累。為考察SINN的性能，即考察當n和q滿足什么關系時，SINN的性能最佳，將SINN輸入節點n和序列長度q分別取為表1所示的8種情況，顯然ANN的輸入節點只有m=24一種情形。

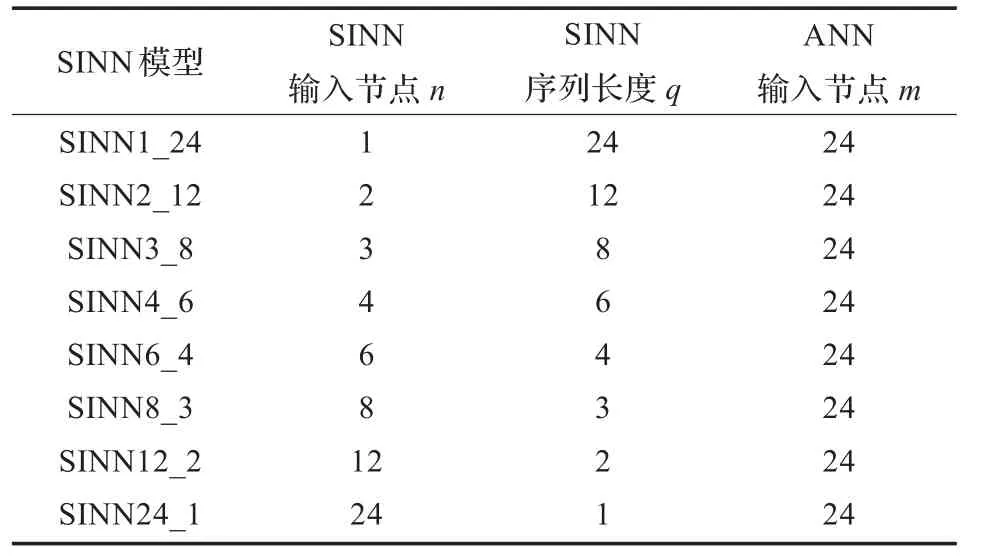
表1 兩種模型的輸入節點和序列長度設置

為便于對比，首先定義收斂的概念。算法終止后，若逼近誤差小于限定誤差，稱算法收斂。

對于輸入節點和隱層節點的每種組合，分別用兩種模型仿真10次，并記錄每種模型的平均逼近誤差、平均迭代步數、平均收斂次數作為評價指標。仿真結果表明，SINN3_8、SIQNN4_6、SIQNN6_4、SIQNN8_3這四種SINN的逼近能力明顯優于ANN。兩種模型的訓練結果對比如圖4～6所示。

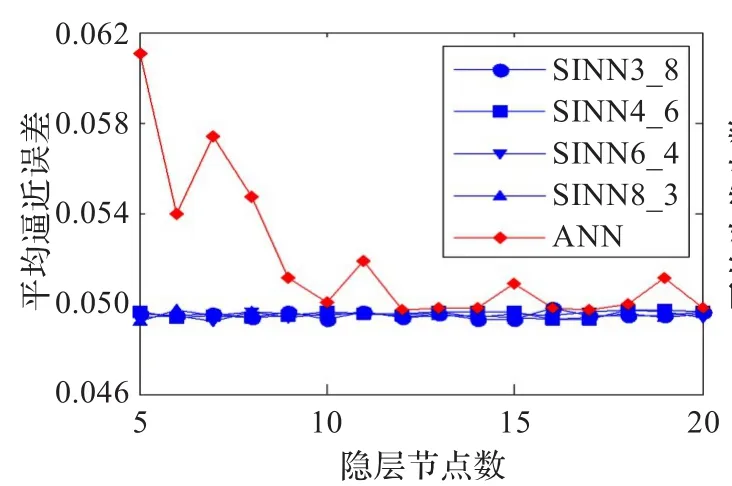
圖4 平均逼近誤差對比

圖5 平均迭代步數對比

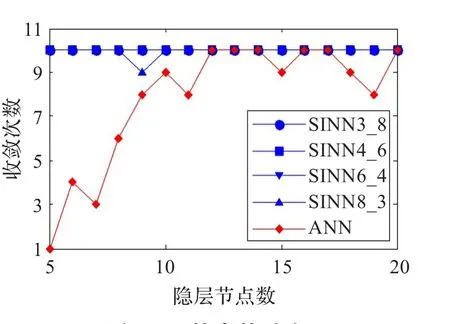
圖6 收斂次數對比

4.2 太陽黑子數年均值預測

太陽黑子是太陽活動中最基本、最明顯的活動現象。太陽黑子產生的帶電離子，可以破壞地球高空的電離層，使大氣發生異常，還會干擾地球磁場，從而使電訊中斷，因此研究太陽黑子的變換規律有著重要的現實意義。本節利用觀測數據，采用SINN建立太陽黑子的預測模型，并通過與ANN和PNN對比，驗證SINN的優越性。

4.2.1 構造樣本數據

實驗采用太陽黑子的年度平均值序列作為仿真對象，從1749年至2007年，共計259個數據。該數據呈現高度非線性，致使常規預測模型很難湊效。其分布特征如圖7所示。

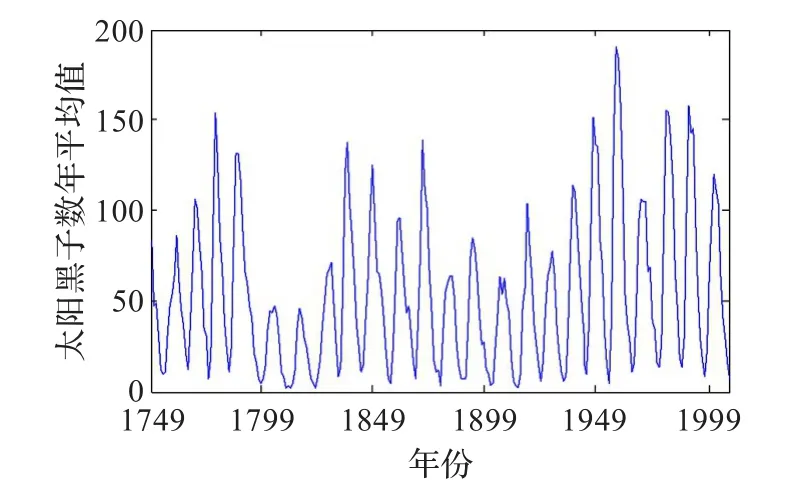
圖7 1749—2007年太陽黑子數據

樣本數據的構造方法是：用連續24年的數據預測其后1年的太陽黑子數。例如用1749—1773年數據預測1774年的太陽黑子數，以此類推。用1749—1948年共200年的數據構造訓練樣本集，完成模型訓練。用余下的59個樣本作為測試集，以檢驗模型的預測能力。

4.2.2 模型參數設置

本仿真將SINN與采用L-M算法的ANN和PNN對比。隱層均分別取10，11，…，25個節點。根據上節結果，僅考察SINN3_8、SINN4_6、SINN6_4、SINN8_3四種模型。限定誤差取0.05，限定步數取1 000。PNN輸入輸出均為一個節點，正交基采用24個Fourier基函數。

4.2.3 訓練結果對比

對于隱層節點的每種取值，分別用ANN、PNN和四種SINN訓練10次，并統計平均逼近誤差、平均迭代步數、收斂次數，作為評價指標。訓練結果對比如圖8～10所示。

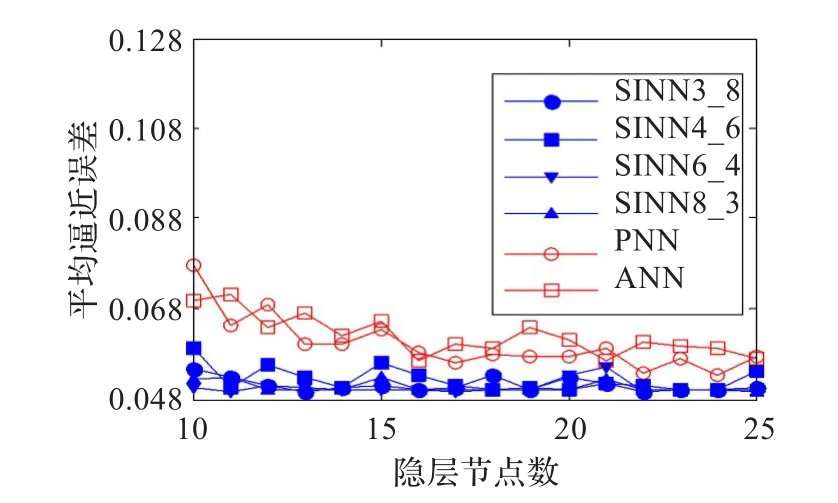
圖8 平均逼近誤差對比

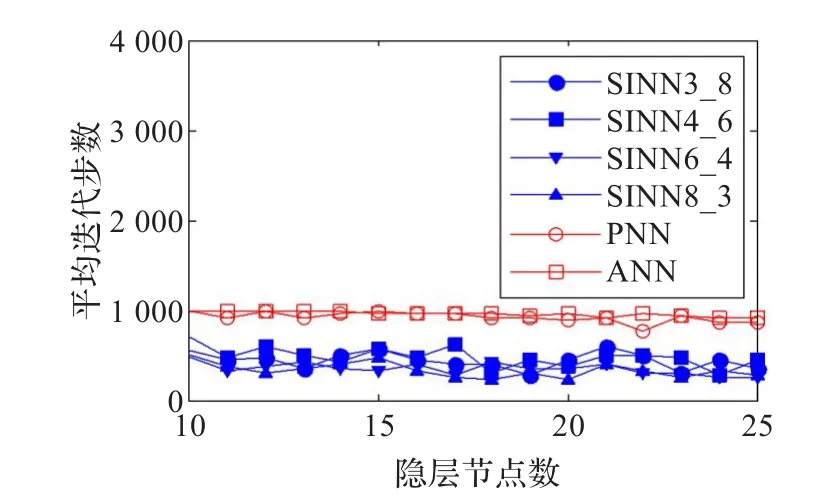
圖9 平均迭代步數對比

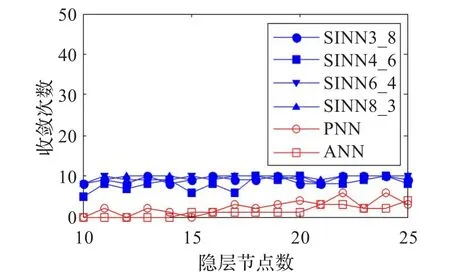
圖10 收斂次數對比

4.2.4 預測結果對比

下面考察SINN和PNN、ANN的預測性能對比。以隱層20個節點為例，將ANN、PNN和4種SINN分別用訓練集訓練10次，每次訓練之后，不論是否收斂，立即用測試集預測，然后統計最大誤差Emax、誤差均值Eavg、誤差方差Evar這三項指標的10次預測平均值，對比結果如表2所示，以SINN 4_6為例，對比曲線如圖11所示。

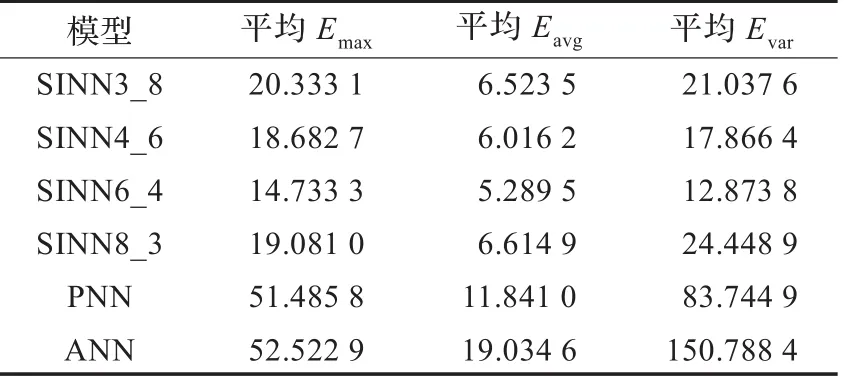
表2 預測指標對比

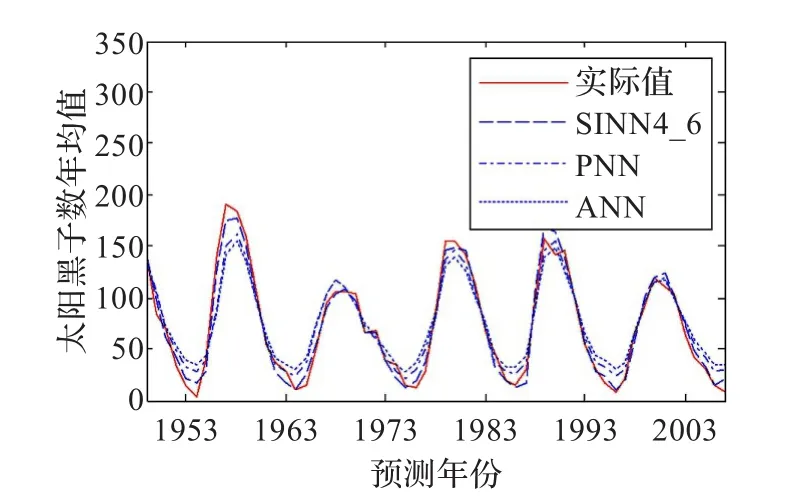
圖11 SINN4_6和PNN、ANN的預測結果對比

4.3 仿真結果分析

綜合以上兩個仿真結果可知，當輸入節點n和序列長q比較接近時，SINN的逼近及預測能力明顯好于PNN和ANN。對此可作如下分析。SINN直接接收離散序列，通過兩次映射將輸入序列循環地映射為隱層序列神經元的輸出，由于序列神經元采用了更多可調的權值，所以SINN有更強的逼近能力。從SINN算法可以看出，輸入節點可以視為模式記憶的寬度，而序列長度可以視為模式記憶的深度，當寬度和深度適當匹配時，SINN呈現出明顯優于PNN和ANN的性能。對于PNN由于只能以深度方式獲取樣本信息，加之正交基展開帶來的截斷誤差，必然導致逼近能力下降。對于ANN，由于只能接收幾何點式的向量輸入，即只能以寬度方式而不能以深度方式獲取樣本信息，因此在ANN的信息處理過程中，不可避免地存在樣本信息的丟失，從而使逼近能力受到影響。

5 結論

本文提出了一種基于序列輸入的神經網絡模型及算法。仿真結果揭示出，該模型可以使SINN從寬度和深度兩方面高效地獲取樣本信息，當輸入節點和序列長度比較接近時可明顯提高其逼近和泛化能力。

[1]Tsoi A C.Locally recurrent globally feed forward networks：a critical review of architectures[J].IEEE Transactions on Neural Networks，1994，7（5）：229-239.

[2]Wu X D，Wang Y N.Extended and Unscented Kalman filtering based feed-forward neural networks for time series prediction[J].Applied Mathematical Modelling，2012，36：1123-1131.

[3]Sven F C，Nikolaos K.Feature selection for time series prediction-A combined filter and wrapper approach for neural networks[J].Neurocomputing，2010，73：1923-1936.

[4]Zarita Z，Pauline O.Modified wavelet neural network in function approximation and its application in prediction of time-series pollution data[J].Applied Soft Computing，2011，11：4866-4874.

[5]Garba I，Peng H，Wu J.Nonlinear time series modeling and prediction using functional w eights wavelet neural network-based state-dependent AR model[J].Neurocomputing，2012，86：59-74.

[6]Durdu O F.A hybrid neural network and ARIMA model for water quality time series prediction[J].Engineering Applications of Artificial Intelligence，2010，23：586-594.

[7]Lee C M，Ko C N.Time series prediction using RBF neural networks with a nonlinear time-varying evolution PSO algorithm[J].Neurocomputing，2009，73：449-460.

[8]Hossein M.Long-term prediction of chaotic time series with multi-step prediction horizons by a neural network with Levenberg-Marquardt learning algorithm[J].Chaos，Solitons and Fractals，2009，41：1975-1979.

[9]何新貴，梁久禎，許少華.過程神經元網絡的訓練及其應用[J].中國工程科學，2001，3（4）：31-35.

[10]He X G，Liang J Z.Procedure Neural Networks[C]//Proceedings of Conference on Intelligent Information Proceeding.Beijing：Publishing House of Electronic Industry，2000：143-146.

[11]何新貴，梁久禎.過程神經元網絡的若干理論問題[J].中國工程科學，2000，2（12）：40-44.

[12]Ye T，Zhu X F.The bridge relating process neural networks and traditional neural networks[J].Neurocomputing，2011，74：906-915.

[13]許少華，何新貴，李盼池.自組織過程神經網絡及其應用研究[J].計算機研究與發展，2003，40（11）：1612-1615.

[14]許少華，何新貴.徑向基過程神經元網絡及其應用研究[J].北京航空航天大學學報，2004，30（1）：14-17.

[15]許少華，何新貴.一種級聯過程神經元網絡及其應用研究[J].模式識別與人工智能，2004，17（2）：201-211.

XIAO Hong,LI Panchi

School of Computer&Information Technology,Northeast Petroleum University,Daqing,Heilongjiang 163318,China

To enhance the approximation capability of neural networks,a sequence input-based neural networks model, whose input of each dimension is a discrete sequence,is proposed.This model concludes three layers,in which the hidden layer consists of sequence neurons,and the output layer consists of common neurons.The inputs are multi-dimensional discrete sequences,and the outputs are common real value vectors.The discrete values in input sequence are in turn weighted and mapped,and then these mapping results are weighted and mapped for the output of sequence neurons in hidden layer,the networks outputs are obtained.The learning algorithm is designed by employing the Levenberg-Marquardt algorithm.The simulation results show that,when the number of the input nodes is relatively close to the length of the sequence, the proposed model is obviously superior to the common artificial neural networks.

neural networks;sequence neuron;sequence neural networks;algorithm design

A

TP18

10.3778/j.issn.1002-8331.1209-0260

XIAO Hong,LI Panchi.Algorithm and application of sequence input-based neural network model.Computer Engineering and Applications,2014,50（16）：62-66.

國家自然科學基金（No.61170132）；黑龍江省教育廳基金（No.11551015，No.11551017，No.12511009，No.12511012）。

肖紅（1979—），女，講師，研究領域為神經網絡和優化算法；李盼池（1969—），男，博士后，教授，研究領域為量子神經網絡和量子優化算法。E-mail：lipanchi@vip.sina.com

2012-09-23

2012-12-06

1002-8331（2014）16-0062-05

CNKI網絡優先出版：2012-12-20,http://www.cnki.net/kcms/detail/11.2127.TP.20121220.1652.002.htm l