錐體彈頭的嵌入式大氣數據傳感系統組合算法*

張 勇，肖前貴，陸宇平，肖地波

(1.南京航空航天大學 無人機研究院，江蘇 南京 210016； 2.南京航空航天大學 自動化學院，江蘇 南京 210016； 3.南京航空航天大學 航天學院，江蘇 南京 210016)

錐體彈頭的嵌入式大氣數據傳感系統組合算法*

張 勇1，肖前貴1，陸宇平2，肖地波3

(1.南京航空航天大學 無人機研究院，江蘇 南京 210016； 2.南京航空航天大學 自動化學院，江蘇 南京 210016； 3.南京航空航天大學 航天學院，江蘇 南京 210016)

嵌入式大氣數據傳感(FADS)系統空氣動力學模型基于鈍頭體推導，該模型適用于錐頭體解算大氣數據，但存在一定的模型誤差。為消除模型誤差，分析了錐頭體模型誤差產生的機理，提出了一種FADS系統組合算法，并對某一典型錐體彈頭進行了仿真驗證。仿真結果表明：動靜壓相對誤差在0.05 %以內，每組大氣數據解算平均耗時在20 ms以內，該算法有效提高了大氣數據解算精度和實時性。

嵌入式大氣數據傳感系統；錐頭體；模型誤差；組合算法

0 引 言

嵌入式大氣數據傳感(flush air data sensing,FADS)系統依靠分布在飛行器前端的壓力傳感器陣列來測量飛行器表面的壓力，并由壓力分布間接獲得飛行參數。FADS系統在大迎角飛行，減小雷達反射面積，高超聲速飛行等方面有著與傳統大氣數據測量系統無法比擬的優勢[1]。在FADS系統的研究和應用上，美國進行了大量的研究,并取得大量成果，形成了成熟技術并應用于航空工業中。國內的FADS系統研究起步較晚，主要有方習高[2]、鄭成軍[3]、鄭守鐸[4]、葉瑋[5]、楊雨等人[6]在FADS系統框架、求解算法、故障檢測、FADS/INS系統組合以及互補濾波技術在FADS系統中的應用方面取得了一系列階段性成果，上述研究成果均以鈍頭體飛行器為研究對象。

對圓錐體外形，要建立表面壓力分布與大氣數據參數的模型非常困難。已有的FADS系統空氣動力學模型是在球體上建立的，采用形壓系數來適應在非球體外形上的應用，這使得該模型有可能適用于圓錐體外形。目前，只有文獻[7]驗證了FADS系統空氣動力學模型在錐頭體飛行器適用性問題，仿真結果表明，根據鈍頭體推導的FADS系統空氣動力學模型應用于錐頭體飛行器存在一定的模型誤差，但文獻[7]未進一步對模型誤差機理進行分析。為進一步消除模型誤差，文獻[7]中采用多項式擬合校準的方法，該方法雖然有效減小了模型誤差，但模型誤差改善效果會隨著多項式次數的增加而趨于飽和。因此，根據模型誤差產生的機理和文獻[7]中解算方法的局限性，本文提出了一種精度和實時性更好的FADS系統解算方法。

1 FADS系統模型

對于典型的鈍頭體，FADS系統動力學模型為[7]

p(θi)=qc(cos2θi+εsin2θi)+p∞,

(1)

cosθi=cosαecosβecosλi+sinβesinφisinλi+ sinαecosβecosφisinλi,

(2)

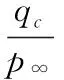
(3)

ε=f(αe,βe,Ma).

(4)

其中，p(θi),θi,φi,λi分別為第i個測壓孔的壓力值、入射角、圓周角、圓錐角；qc為動壓，p∞為靜壓，ε為無量綱的形壓系數，αe,βe分別為當地迎角和當地側滑角，Ma為馬赫數。

2 FADS系統模型誤差分析

上述模型中式(1)～式(3)是顯式的數學公式，而式(4)是需要根據實驗數據飛行前確定。該模型是在球體上建立的，采用形壓系數來適應在非球體外形上的應用。

根據壓力分布情況計算當地迎角αe和當地側滑角βe[8]，利用式(2)計算各測壓孔處的氣流入射角θi。

對于一組飛行參數(α,β,Ma)，利用cos2θi=1-sin2θi，將式(1)改寫成

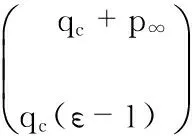
(5)

寫成矩陣形式

工作區地下水主要接受大氣降水入滲補給和地表水側向補給。巖溶裂隙、孔隙是地下水的主要徑流通道，地下水總體徑流方向與地表水徑流方向基本一致，即由北西向南東徑流。地下水排泄形式以泉、潛流及井為主。

P=AX.

(6)

其中

P=[p(θ1) …p(θn)]T,

(7)

(8)

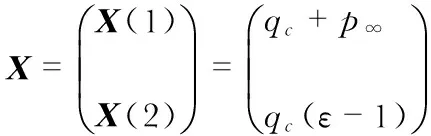
(9)

根據線性方程組的求解理論，得到X的最小二乘解

X=A+P.

(10)

再根據式(3)計算出不同馬赫數時的qc/p∞，然后就可以算出該組飛行參數對應的形壓系數

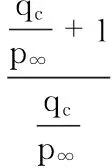
(11)

即得到了一組(α,β,Ma)對應的ε。取一系列的(α,β,Ma)k組合，重復以上步驟，可以得到對應的形壓系數序列εk，即得到ε隨(α,β,Ma)變化的關系。

根據已知的馬赫數，利用式(3)，求出動靜壓之比

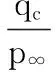
(12)

由于式(3)中馬赫數與動靜壓之比的關系對各種外形(包括錐頭體和鈍頭體)的飛行器均適用的，因此,可認為式(12)得到的動靜壓之比是足夠精確的，可以由此來確定真實的動靜壓。

簡化分析，對動靜壓進行歸一化處理，即靜壓為1，動壓就等于動靜壓之比，即得到動靜壓的真實值

(13)

采用式(5)～式(10)的過程求出X，再根據已知馬赫數求出動靜壓之比g，可以得到根據模型(1)計算的動壓和靜壓值

(14)

模型動壓和靜壓的相對誤差

(15)

由式(14)和式(15)可見，模型動壓誤差和模型靜壓誤差相當。實際上，根據式(9) 和式(10)可以看出，調整形壓系數ε可以改變靜壓或者動壓，但是動靜壓之和X(1)與形壓系數無關。式(1)用形壓系數來滿足不同外形的前提是式(1)必須能夠測得準確的總壓(動靜壓之和)，然后通過調整形壓系數可以改變動靜壓在總壓中占的比重。而通過以上分析發現，對文獻[7]中研究的錐頭體外形，式(1)并不能準確算出總壓。因此，通過調整形壓系數，可以使得動壓或者靜壓中的一個準確，但卻使得另外一個更加不準確，即無法通過改變形壓系數使得動壓和靜壓同時精確。

3 FADS系統組合算法

由上一節分析可知，通過調整形壓系數不能減小FADS系統模型誤差。式(1)～式(4)描述的模型誤差主要是動壓和靜壓誤差，迎角和側滑角誤差基本由校準方法決定。

雖然單個神經網絡的方法能滿足大氣數據的計算精度要求，但由于采用單一神經網絡計算所有大氣數據增大了故障管理難度和訓練復雜度[10]。因此，為有效消除模型誤差和提高工程實現性，采用分層計算的方式實現FADS系統解算。采用三點法和校準算法求解迎角和側滑角，再采用神經網絡校準動靜壓，降低網絡的輸出維數，最后根據計算所得的動靜壓值求解馬赫數。

這樣可以將整個FADS系統算法分成三層：三點法和校準算法求解迎角α和側滑角β；神經網絡法求解動壓qc和靜壓p∞；根據動靜壓計算馬赫數Ma。組合算法流程圖如圖1。

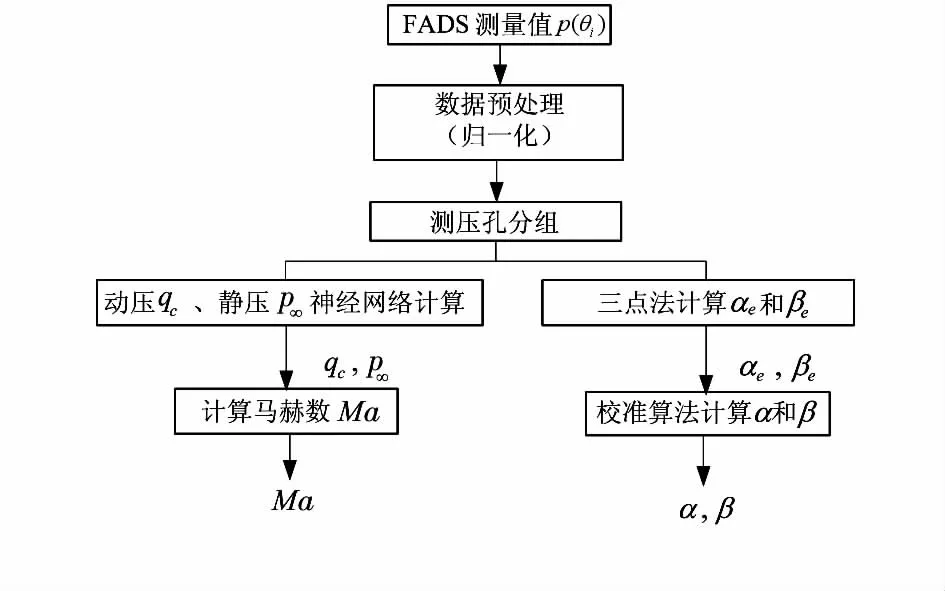
圖1 組合算法流程Fig 1 Flow chart of combinatorial algorithm

RBF網絡具有強大的函數逼近功能，并且比BP網絡設計更加簡單，它將自動選擇神經元個數，傳輸函數為徑向基函數。組合算法中動靜壓求解采用RBF神經網絡，RBF神經網絡構建方法參見文獻[11]。神經網絡在訓練中確定了權值和閾值，在線計算也是簡單的數學運算，因此,該算法進一步提高了算法的實時性。

4 仿真驗證

采用文獻[7]中的錐體彈頭外形和壓力數據，采用組合算法進行大氣數據解算。由于迎角和側滑角的解算與文獻[7]相同，并且錐頭體的模型誤差體現在動靜壓誤差方面，因此,本文著重比較動靜壓的求解精度。

本次設計中，RBF神經網絡求解動靜壓，其徑向基函數的密度常數選取為spread=0.55。將迎角α=-8°～8°、側滑角β=0°,±2°,±4°時的壓力數據作為RBF神經網絡訓練樣本數據，并將α=-8°～8°,β=±1°,±3°時壓力數據作為測試樣本。組合算法解算得到的動壓與靜壓相對誤差如圖 2和圖 3。

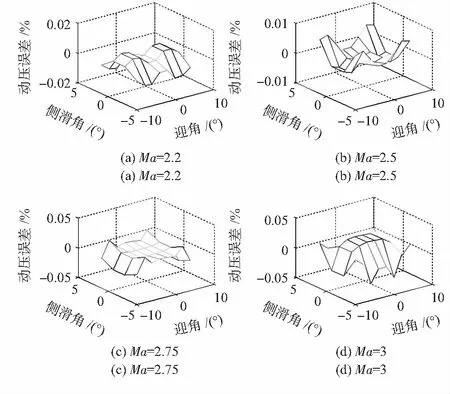
圖2 動壓相對誤差Fig 2 Relative errors of dynamic pressure

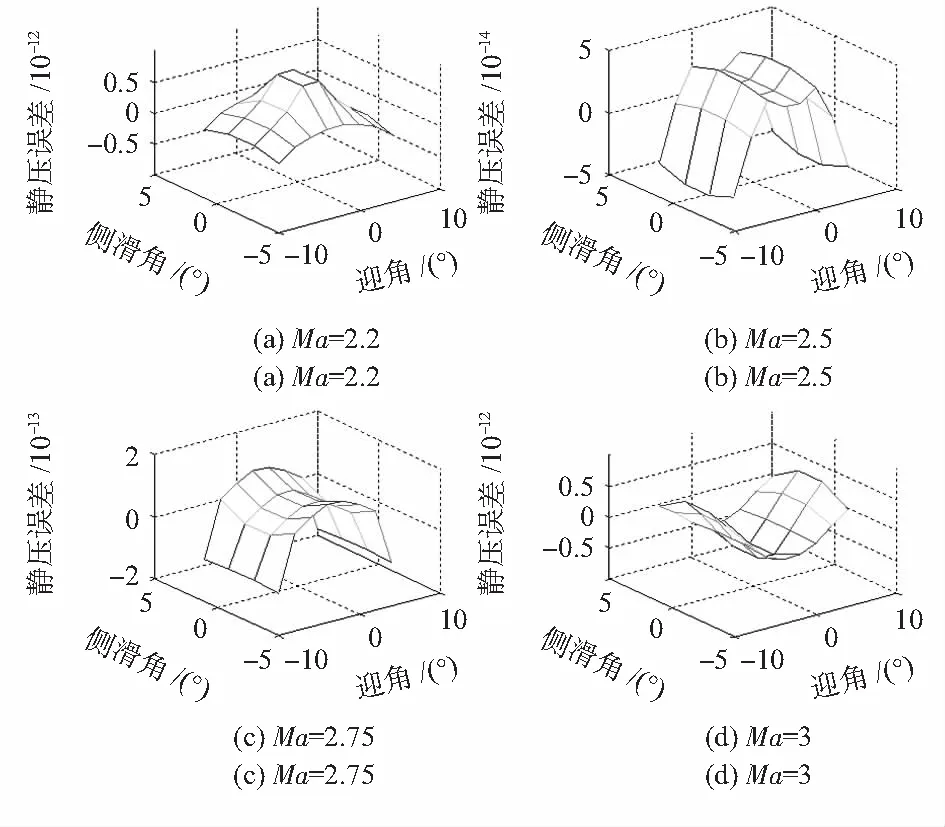
圖3 靜壓相對誤差Fig 3 Relative errors of static pressure

由圖 2和圖 3可知，本文的組合算法相比文獻[7]中的校準算法精度更高，動壓相對誤差控制在0.05 %以內，靜壓相對誤差達到10-12量級。

進一步，仿真對比本文組合算法和文獻[7]中的校準算法解算時間。在同一臺計算機對兩種算法進行測試，測試128組大氣數據，得到每組大氣數據平均耗時如表 1。由表1可知，本文組合算法的平均一組大氣數據解算時間小于20 ms，相比文獻[7]大大縮短了大氣數據的解算時間。

表1 平均一組大氣數據解算時間Tab 1 Average resolving time of a set of air datas

5 結 論

本文針對FADS系統空氣動力學模型應用于錐頭體飛行器存在模型誤差的機理進行了分析，分析表明:通過調整形壓系數不能減小FADS系統的模型誤差。針對模型誤差產生的機理，提出了一種FADS系統組合算法，并對其進行了數值仿真驗證。仿真結果表明：動壓與靜壓的相對誤差小于0.05 %，每組大氣數據解算時間小于20 ms，該算法有效提高了算法解算精度和實時性。

[1] Srivastava Ankur ,Meade Andrew J,Mokhtarzadeh Ali Arya.A hybrid data-model fusion approach to calibrate a flush air data sensing system[R].Atlanta:AIAA,2010.

[2] 方習高,陸玉平.嵌入式大氣數據傳感系統求解算法研究[M].計算機測量與控制,2008,16(3):398-400.

[3] Zheng Chenjun,Lu Yuping,He zhen.Improved algorithms for flush airdata sensing system[J].Chinese Journal of Aeronatics,2006,9(4):334-339.

[4] 鄭守鐸,陸宇平,葉 瑋.基于χ2檢驗的FADS系統故障檢測與管理技術研究[J].計算機測量與控制,2007,15(11):1449-1551.

[5] 葉 瑋,鄭守鐸,溫瑞珩.FADS/INS組合法迎角、側滑角測量方法研究[J].飛機設計,2007,27(6):14-17.

[6] 楊 雨,陸宇平,吳在桂.嵌入式大氣數據傳感系統中的組合濾波技術[J].傳感器與微系統,2009,28(5):117-120.

[7] 張 勇,肖前貴,陸宇平,等.一種適用錐頭體的嵌入式大氣數據傳感系統改進校準算法[J].計算機測量與控制,2014,22(5):1513-1515.

[8] Cobleigh Brent R,Whitmore Stephen A,Haering Edward A.Flush airdata sensing (FADS) system calibration procedures and results for blunt forebodies[C]∥Dryden Flight Research Center Edwards,California,1999.

[9] Edward J Artz,Nicholas W Dona,Dr Thomas R.Yechout.NASA orion flush air data sensing system feasibility determination and development[C]∥The 52nd Aerospace Sciences Meeting,Maryland,2014.

[10] 肖地波，陸宇平，吳在桂.嵌入式大氣數據傳感系統求解算法研究[M].北京：科學出版社，2010.

[11] 魏海坤.神經網絡結構設計的理論與方法[M].北京:國防工業出版社,2005.

Combinatorial algorithm of flush air data sensing system for cone forebodies*

ZHANG Yong1, XIAO Qian-gui1, LU Yu-ping2, XIAO Di-bo3

(1.Research Institute of Unmanned Aircraft Vehicle，Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China; 2.College of Automatic Engineering，Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China; 3.College of Astronautics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)

The aerodynamic model of flush air data sensing (FADS) system,which is derived from blunt forebodies,is suitable for cone forebodies,however,the model error is subsistent when the aerodynamic model is applied to cone forebodies.To eliminate model error,the mechanism of cone forebody model error is analyzed and a suit of combinatorial algorithm for FADS is proposed,the corresponding validation of simulation is accomplished for a typical cone forebody.Simulation results show that relative errors of dynamic pressure and static pressure are less than 0.05 % and average resolving time consuming of a set of air data is less than 20 ms,respectively,thus solving precision and real-time performance are improved effectively by the algorithm.

flush air data sensing(FADS) system; cone forebody; model error; combinatorial algorithm

10.13873/J.1000—9787(2014)10—0148—03

2014—07—28

江蘇省自然科學基金資助項目(BK20130817)；南京航空航天大學基本科研業務費資助項目(NS2014404)

V 241.6

A

1000—9787(2014)10—0148—03

張 勇(1986-)，男，浙江衢州人，工學碩士，研究實習員，主要從事飛行控制方向的研究。