永磁同步電動(dòng)機(jī)結(jié)構(gòu)的模態(tài)研究*

李 娉 馬永龍

(1.湖北三江航天險(xiǎn)峰電子信息有限公司 武漢 432000)(2.海軍駐中南地區(qū)光電系統(tǒng)軍事代表室 武漢 430074)

永磁同步電動(dòng)機(jī)結(jié)構(gòu)的模態(tài)研究*

李 娉1馬永龍2

(1.湖北三江航天險(xiǎn)峰電子信息有限公司 武漢 432000)(2.海軍駐中南地區(qū)光電系統(tǒng)軍事代表室 武漢 430074)

論文先簡(jiǎn)要介紹模態(tài)分析理論,再運(yùn)用機(jī)電類(lèi)比的方法推導(dǎo)定子固有頻率的計(jì)算方法,并用ANSYS軟件對(duì)電機(jī)定子建立的三維有限元模型進(jìn)行模態(tài)分析,計(jì)算出它們的固有頻率及其振型,避免和電磁力的頻率及次數(shù)發(fā)生共振,從而降低永磁同步電動(dòng)機(jī)的電磁振動(dòng)和噪聲。

永磁同步電動(dòng)機(jī); 模態(tài)分析; ANSYS

Class Number TM359.4

1 引言

永磁同步電動(dòng)機(jī)的電磁振動(dòng)與噪聲不僅與電機(jī)中氣隙磁場(chǎng)所產(chǎn)生的電磁激振力波頻率、幅值和力波階數(shù)有關(guān),而且還與電機(jī)結(jié)構(gòu)的固有頻率的大小及分布有著密切的關(guān)系。通過(guò)對(duì)電機(jī)定子結(jié)構(gòu)的模態(tài)分析,可以確定電機(jī)電樞結(jié)構(gòu)的固有頻率和振型,就可預(yù)測(cè)電機(jī)在電磁力的作用下實(shí)際振動(dòng)響應(yīng)。

模態(tài)分析技術(shù)從20世紀(jì)60年代后期發(fā)展至今已經(jīng)有40多年的歷史了。模態(tài)分析的經(jīng)典性定義是:將線性定常系統(tǒng)振動(dòng)微分方程組中的物理坐標(biāo)變換為模態(tài)坐標(biāo),使方程組解藕,成為一組以模態(tài)坐標(biāo)及模態(tài)參數(shù)描述的獨(dú)立方程,以便求出系統(tǒng)的模態(tài)參數(shù)[1]。振動(dòng)模態(tài)是振動(dòng)系統(tǒng)的各點(diǎn)以特定的頻率作簡(jiǎn)諧振動(dòng)時(shí),表示波節(jié)和波腹的振動(dòng)形態(tài)或與其相應(yīng)的衰減振動(dòng)狀態(tài);固有模態(tài)是自由振動(dòng)時(shí)系統(tǒng)的振動(dòng)模態(tài),與系統(tǒng)的各個(gè)自由度相對(duì)應(yīng),常簡(jiǎn)稱(chēng)為模態(tài)[2]。模態(tài)是機(jī)械及結(jié)構(gòu)的固有振動(dòng)特性。每一階模態(tài)具有特定的固有頻率、阻尼比和模態(tài)振型。這些模態(tài)參數(shù)可以由有限元計(jì)算或試驗(yàn)分析取得。基于線性疊加原理,一個(gè)復(fù)雜的振動(dòng)系統(tǒng)可以分解為許多模態(tài)的疊加。這樣一個(gè)分析過(guò)程為模態(tài)分析[3]。

永磁同步電動(dòng)機(jī)結(jié)構(gòu)的模態(tài)分析是判斷電動(dòng)機(jī)定子結(jié)構(gòu)是否發(fā)生共振的重要手段,電動(dòng)機(jī)的電磁噪聲和振動(dòng)主要是通過(guò)定子、殼體向外輻射。本節(jié)主要是進(jìn)行電動(dòng)機(jī)結(jié)構(gòu)的模態(tài)分析,由于電動(dòng)機(jī)結(jié)構(gòu)的幾何特性決定著定子沿軸向的剛度是變化的,所以采用三維結(jié)構(gòu)有限元模型來(lái)分析電動(dòng)機(jī)定子及機(jī)殼結(jié)構(gòu)的模態(tài)。

2 電機(jī)結(jié)構(gòu)的模態(tài)分析理論

永磁同步電動(dòng)機(jī)模態(tài)分析的關(guān)鍵在于找到模態(tài)振型矩陣,以構(gòu)成模態(tài)坐標(biāo)系統(tǒng),并求得響應(yīng)量在這一坐標(biāo)系統(tǒng)中的坐標(biāo),具體過(guò)程如下[4]:

1) 尋找各階模態(tài)振型,組成坐標(biāo)變換矩陣{ψr}=[{ψ1} {ψ2} {ψ3} … {ψN}];

2) 進(jìn)行坐標(biāo)變換{X}={ψ}{q};

3) 求取模態(tài)坐標(biāo)qr,r=1,2,3,…,N,從而得到{q};

4) 建立響應(yīng)計(jì)算模型—模態(tài)模型;運(yùn)用模態(tài)模型,便可計(jì)算在實(shí)際激勵(lì)作用下的結(jié)構(gòu)的運(yùn)動(dòng),包括位移、速度、加速度,乃至應(yīng)力應(yīng)變。

2.1 質(zhì)點(diǎn)運(yùn)動(dòng)方程

通過(guò)牛頓第二定律可以得到質(zhì)點(diǎn)的運(yùn)動(dòng)方程:

(1)

進(jìn)行拉普拉斯變換后上式可寫(xiě)為

s2mX(s)+srX(s)+kX(s)=F(s)

兩邊同除以m可變換為

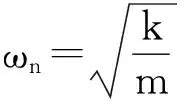
則質(zhì)點(diǎn)的位移響應(yīng)為

質(zhì)點(diǎn)的速度響應(yīng)為

質(zhì)點(diǎn)的加速度響應(yīng)為

因此可得出由力到加速度的傳遞函數(shù)為

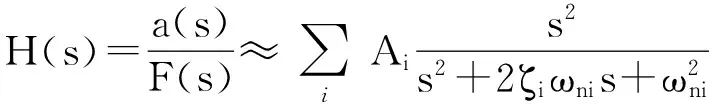
永磁同步電動(dòng)機(jī)定子振動(dòng)中,除了有電磁力引起的強(qiáng)迫振動(dòng),還有自由振動(dòng)。下面分析永磁同步電動(dòng)機(jī)的自由振動(dòng)特性。令系統(tǒng)的運(yùn)動(dòng)方程(1)的右邊為0,則可得系統(tǒng)的自由振動(dòng)方程為

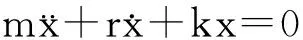
該方程的通解形式為

式中,C1、C2為由系統(tǒng)初始條件決定的常數(shù)。

故運(yùn)動(dòng)方程的解可表示為

對(duì)于無(wú)阻尼運(yùn)動(dòng),ζ=0;對(duì)于欠阻尼運(yùn)動(dòng),ζ<1;對(duì)于臨界阻尼運(yùn)動(dòng),ζ=1對(duì)于過(guò)阻尼運(yùn)動(dòng),ζ>1。在實(shí)際的振動(dòng)系統(tǒng)中,一般都是欠阻尼運(yùn)動(dòng),否則就不會(huì)形成振動(dòng)了。則對(duì)于欠阻尼情況,ζ2?1,運(yùn)動(dòng)方程的解可寫(xiě)為

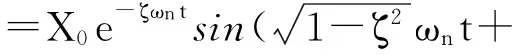
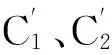
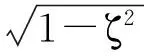
2.2 永磁同步電動(dòng)機(jī)振動(dòng)特性的機(jī)電類(lèi)比分析

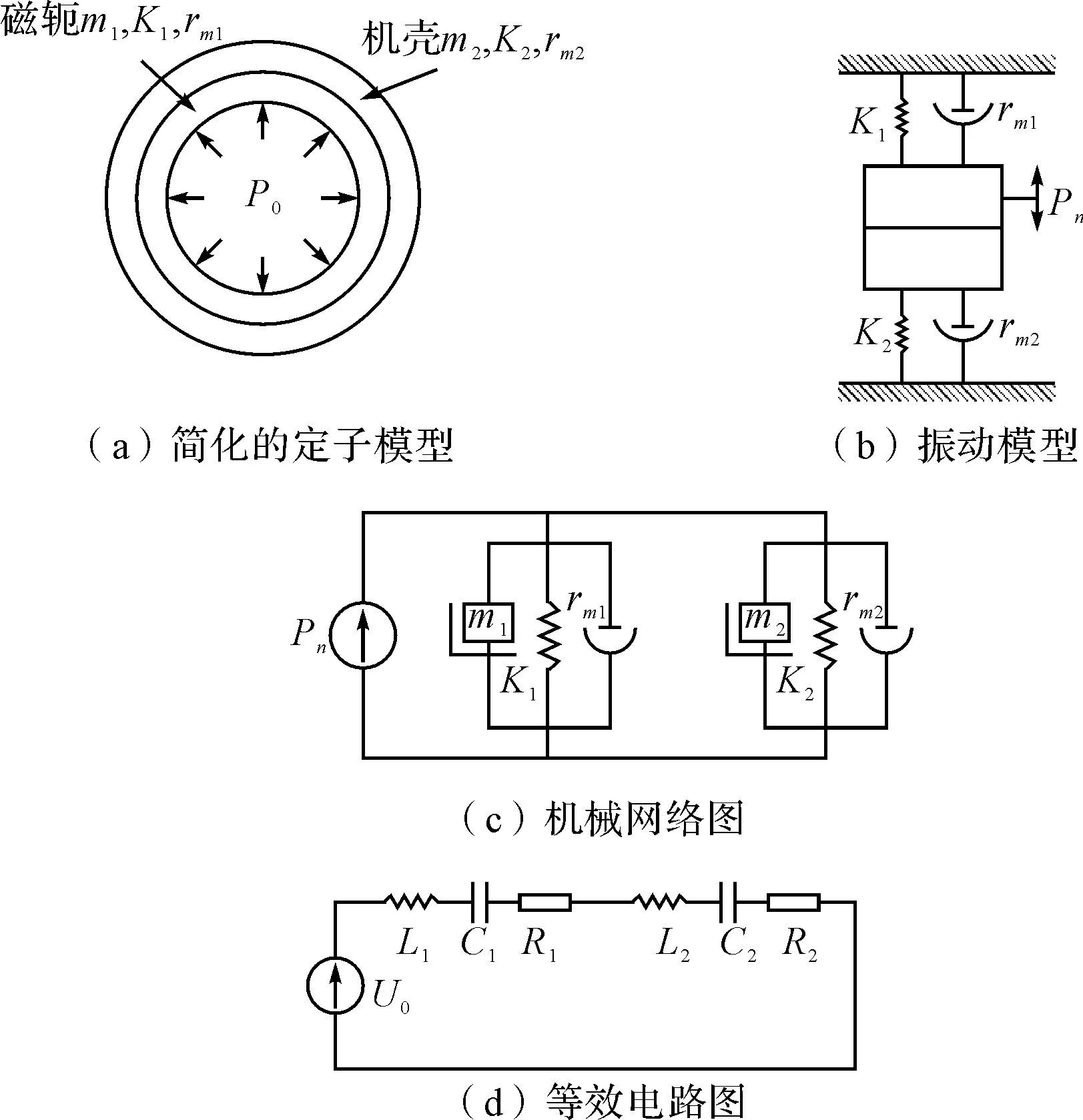
圖1 電機(jī)定子機(jī)電類(lèi)比雙環(huán)型模型

永磁同步電動(dòng)機(jī)一般選用同容量的異步電機(jī)機(jī)座,定子鐵心與機(jī)殼內(nèi)圓采用過(guò)盈配合,無(wú)連接筋。設(shè)定子鐵心軛的剛度為K1,質(zhì)量為m1,機(jī)殼的剛度為K2,質(zhì)量為m2,不考慮繞組、定子凸極的影響,散熱筋、底腳、接線盒的質(zhì)量歸入機(jī)殼質(zhì)量;并設(shè)各部分的阻尼系數(shù)分別為rm1、rm2(假設(shè)各部分阻尼比為粘性,且等于鋼或鑄鐵的阻尼比),則其物理模型、機(jī)械網(wǎng)絡(luò)圖、等效電路圖如圖1所示[5～6]。

圖中p0為作用在定子鐵心內(nèi)表面上單位面積力的幅值,pn為等效的集中力,即:

Pn=2πRilaP0

式中,Ri為定子磁軛的內(nèi)半徑,la為定子鐵心軸向長(zhǎng)度。

由機(jī)電類(lèi)比法[7]可得對(duì)應(yīng)角頻率ω的總機(jī)械阻抗為

則定子振動(dòng)位移的幅值為

(2)

式中,鐵心及機(jī)殼的剛度和質(zhì)量為[3]

(3)

(4)

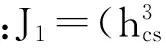
設(shè)定子鐵芯、機(jī)殼的阻尼比ζ1、ζ2為粘性,則阻尼系數(shù)為

令機(jī)械阻抗的虛部為零,可求得定子的固有頻率為

(5)

共振時(shí),定子振動(dòng)位移的振幅為

將式(3)、(4)代入式(2)、(5),可得電機(jī)強(qiáng)迫振動(dòng)幅值和固有頻率為

(6)

(7)

由式(6)～(7)可得永磁電機(jī)軸向階數(shù)為零的平面振動(dòng)特性[6],即:

1) 振動(dòng)幅值與力波幅值成正比。因此減小力波幅值是控制振動(dòng)的主要措施之一;

2) 隨著振形階數(shù)n的增大,對(duì)應(yīng)的固有頻率近似以n2的比例增大,而振幅則近似以n4的比例減小,因此,階數(shù)較低的力波引起的振動(dòng)應(yīng)是防范的重點(diǎn);

3) 定子直徑越大,固有頻率越低,亦即當(dāng)激勵(lì)力的振幅、頻率均相等時(shí),幾何尺寸越大的電機(jī),振動(dòng)幅值越大,因而磁噪聲級(jí)亦越大;

4) 振動(dòng)大小與振動(dòng)系統(tǒng)的阻抗Zm關(guān)系很大,阻抗表明振動(dòng)系統(tǒng)接近諧振的程度。諧振時(shí)振動(dòng)甚至在小的電磁激振力時(shí)都可能很大。因此,使固有頻率避開(kāi)主要的力波頻率是減小振動(dòng)的主要措施之一;

5) 共振時(shí)激振力波與振動(dòng)速度同相位,這時(shí)振動(dòng)幅值完全由阻尼限制。

3 永磁同步電動(dòng)機(jī)定子模態(tài)分析

目前,理論計(jì)算固有頻率的方法有兩大類(lèi):一類(lèi)是解析解計(jì)算方法,典型的是機(jī)電類(lèi)比法,該方法可以得到固有頻率的解析表達(dá)式,但是計(jì)算精度較差;另一類(lèi)是能量法,它有兩種解法,一種是傅里葉級(jí)數(shù)解法,另一種是有限元法。一般情況下,兩種解法都不能得到解析解,而只能得到數(shù)值解。在定子結(jié)構(gòu)對(duì)稱(chēng)時(shí),傅立葉級(jí)數(shù)的求解精度可滿(mǎn)足一般工程上的要求。有限元解法可以考慮定子結(jié)構(gòu)的不規(guī)則性,其計(jì)算精度較高。由于電機(jī)結(jié)構(gòu)復(fù)雜,用解析法計(jì)算雖然簡(jiǎn)便,但計(jì)算誤差較大,因此本文采用有限元方法仿真計(jì)算了電機(jī)的模態(tài),研究了電機(jī)的定子鐵心的模態(tài)。

用戶(hù)使用ANSYS的模態(tài)分析來(lái)決定一個(gè)結(jié)構(gòu)或者機(jī)器部件的振動(dòng)頻率(固有頻率和振型)。ANSYS產(chǎn)品家族的模態(tài)分析是線性分析。任何非線性特性,如塑性和接觸(間隙)單元,即使定義了也將被忽略。

需要記住以下兩個(gè)要點(diǎn)[8]:

1) 模態(tài)分析中只有線性行為是有效的,如果指定了非線性單元,它們將被當(dāng)作是線性的。例如,如果分析中包含了接觸單元,則系統(tǒng)取其初始狀態(tài)的剛度值并且不再改變此剛度值。

2) 必須指定彈性模量EX(或某種形式的剛度)和密度DENS(或者某種形式的質(zhì)量)。材料性質(zhì)可以是線性的或非線性的、各向同性或正交各向異性的、恒定的或與溫度有關(guān)的,非線性特性將被忽略。用戶(hù)必須對(duì)某些指定的單元(COMBIN7,COMBIN14,COMBIN37)進(jìn)行實(shí)常數(shù)的定義。

3.1 基于能量法的電機(jī)振動(dòng)模態(tài)的有限元分析模型

作為有限元法的一種,能量法的基礎(chǔ)是拉格朗日方程。在能量法計(jì)算中,一般用廣義坐標(biāo)來(lái)描述系統(tǒng),將系統(tǒng)的動(dòng)能和勢(shì)能等表示為廣義坐標(biāo)及其導(dǎo)數(shù)的函數(shù)[9]。系統(tǒng)的拉格朗日運(yùn)動(dòng)方程可表示為

其中,L=T-U為拉格朗日函數(shù),T為系統(tǒng)動(dòng)能,U為系統(tǒng)勢(shì)能,Fi為系統(tǒng)非保守廣義力,qi為廣義坐標(biāo),i=1,2,3…。

在有限元解法中,單元的動(dòng)能為

勢(shì)能為

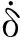
單元的剛度矩陣為

依據(jù)Hamilton原理和應(yīng)力—應(yīng)變、應(yīng)變—位移的關(guān)系[10],可導(dǎo)出電機(jī)離散后單元的運(yùn)動(dòng)方程為

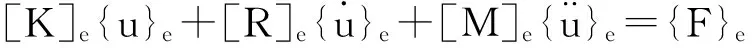
將各個(gè)離散的單元方程組聯(lián)合成總的系統(tǒng)方程組,經(jīng)過(guò)整理則可得出系統(tǒng)標(biāo)準(zhǔn)的運(yùn)動(dòng)方程為

(8)

([K]-ω2[M]){u}={0}

(9)

根據(jù)線性方程組理論有非零解的充分必要條件為

|[K]-ω2[M]|=0

(10)

解出滿(mǎn)足方程(9)、(10)的頻率ω2和對(duì)應(yīng)的非零解向量{ur}(r=1,2,3…),則ωr,{ur}分別為電機(jī)結(jié)構(gòu)的固有頻率和固有振型。

有限元法ANSYS軟件提供了子空間法、分塊Lanczos法、Power Dynamics法、縮減法、非對(duì)稱(chēng)法、阻尼法和QR阻尼法七種模態(tài)提取方法。大多數(shù)分析都選用前四種求解方法,非對(duì)稱(chēng)法和阻尼法只在特殊情況下會(huì)用到。本文主要采用分塊Lanczos方法對(duì)問(wèn)題展開(kāi)求解。此方法應(yīng)用于提取大模型的多階模態(tài),經(jīng)常應(yīng)用在具有實(shí)體單元或殼單元的模型中,特別是在模型中包含形狀較差的實(shí)體和外殼單元中,它的計(jì)算速度很快,但要以消耗內(nèi)存為代價(jià)[11]。

分塊Lanczos法的特征值求解器采用缺省求解器,它采用Lanczos算法,是由一組向量來(lái)實(shí)現(xiàn)Lanczos遞歸運(yùn)算。這種方法和子空間法一樣精確,但速度更快。無(wú)論EQSLV命令指定過(guò)何種求解器進(jìn)行求解,分塊法都將自動(dòng)采用稀疏矩陣方程求解器。計(jì)算某系統(tǒng)特征值譜所包含一定范圍的固有頻率時(shí),采用這種方法特別有效。計(jì)算時(shí),求解從頻率譜中間位置到高頻端范圍內(nèi)的求解收斂速度和求解低階頻率時(shí)基本上一樣快。因此,當(dāng)采用頻移頻率(FREQB)來(lái)提取從FREQB(起始頻率)的模態(tài)時(shí),提取大于FREQB的n階模態(tài)和提取n階低頻模態(tài)的速度基本相同。在本節(jié)的計(jì)算中均采用了這種方法。

3.2 定子鐵芯的模態(tài)分析

永磁同步電動(dòng)機(jī)定子鐵芯的彈性模量通常取2.05～2.15×1011N/m2,密度為7305kg/m2,泊松比是0.3。采用有限元軟件進(jìn)行模態(tài)仿真時(shí),模型選用的單元類(lèi)型為PLANE82,分析類(lèi)型選用分塊的蘭索斯(Block Lanczos)法,求解的模態(tài)數(shù)選擇為40,擴(kuò)展的模態(tài)數(shù)選擇為40。圖2是定子鐵芯三維有限元模型,圖3是模態(tài)分析后的固有頻率及振型。

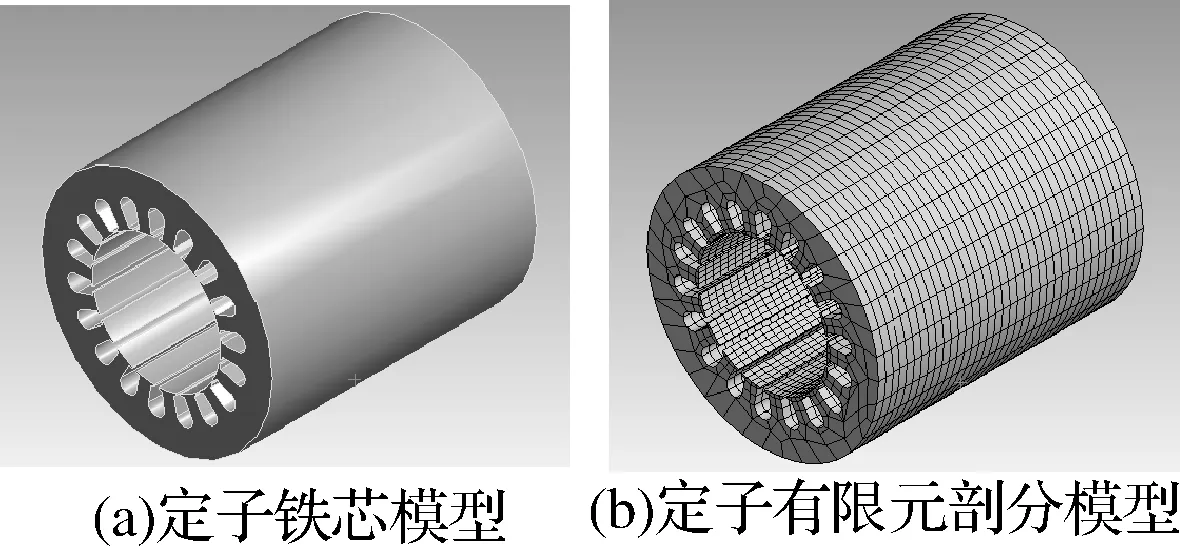
圖2 定子鐵芯三維有限元模型

(a) 二階振型

(b) 三階振型

(c) 四階振型

(d) 五階振型圖3 定子鐵芯模態(tài)分析的固有頻率及振型表1 永磁同步電動(dòng)機(jī)定子三維模型的振型和固有頻率

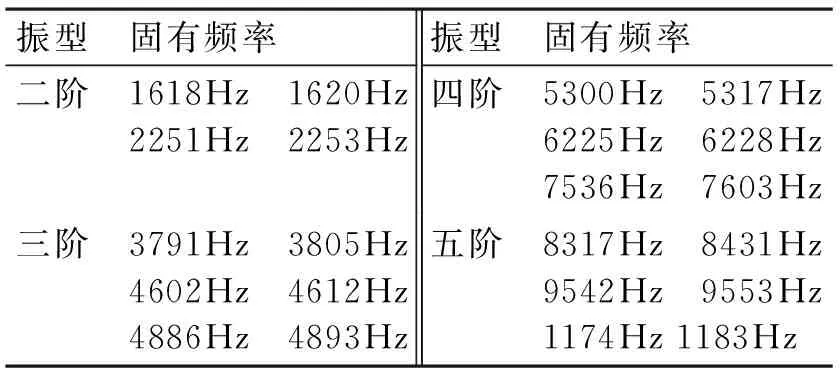
振型固有頻率振型固有頻率二階1618Hz 1620Hz2251Hz 2253Hz四階5300Hz 5317Hz6225Hz 6228Hz7536Hz 7603Hz三階3791Hz 3805Hz4602Hz 4612Hz4886Hz 4893Hz五階8317Hz 8431Hz9542Hz 9553Hz1174Hz1183Hz

從表1中可以看出三維定子模型更加接近實(shí)際模型,可以得到豐富的模態(tài)和固有頻率信息。有些頻率相近是由于電機(jī)定子結(jié)構(gòu)是對(duì)稱(chēng)的,會(huì)出現(xiàn)振型和頻率相同但相位不同的情況;考慮永磁同步電動(dòng)機(jī)定子結(jié)構(gòu)的固有模態(tài),有利于避免電磁共振,減少振動(dòng)幅值,從而有利于降低電磁振動(dòng)和噪聲。

4 結(jié)語(yǔ)

本文運(yùn)用機(jī)電類(lèi)比的方法推導(dǎo)出了定子固有頻率的計(jì)算方法。利用有限元分析軟件ANSYS建立了永磁同步電動(dòng)機(jī)樣機(jī)定子的三維有限元模型,計(jì)算得到了樣機(jī)的振型及振動(dòng)固有頻率的關(guān)系,從而為避免共振起到了預(yù)見(jiàn)性作用,為高轉(zhuǎn)速和低噪聲的永磁同步電動(dòng)機(jī)定子設(shè)計(jì)提供理論參考。

[1] 袁安富,陳俊.ANSYS在模態(tài)分析中的應(yīng)用[J].中國(guó)制造業(yè)信息化,2007,36(11):42-44.

[2] S. J. 楊著.低噪聲電動(dòng)機(jī)[M].北京:科學(xué)出版社出版,1985.

[3] 張培強(qiáng),馮文琴.現(xiàn)代實(shí)驗(yàn)?zāi)B(tài)分析的基本原理[J].武漢水運(yùn)工程學(xué)院學(xué)報(bào),1984,(4):99-115.

[4] 李德葆.振動(dòng)模態(tài)分析及其應(yīng)用[M].北京:宇航出版社,1989:57.

[5] 陳永校,諸自強(qiáng),應(yīng)善成.電機(jī)噪聲的分析與控制[M].杭州:浙江大學(xué)出版社,1987:1-200.

[6] 孫劍波.開(kāi)關(guān)磁阻電機(jī)的減振降噪和低轉(zhuǎn)矩[D].武漢:華中科技大學(xué),2005.

[7] 王宏華,王治平,江泉.開(kāi)關(guān)磁阻電動(dòng)機(jī)固有頻率解析計(jì)算[J].中國(guó)電機(jī)工程學(xué)報(bào),2005,25(12):133-135.

[8] 王建江,胡仁喜,劉英林,等.ANSYS11.0結(jié)構(gòu)與熱力學(xué)有限元分析實(shí)例指導(dǎo)教程[M].北京:機(jī)械工業(yè)出版社,2008,3.

[9] 盛劍霓.工程電磁場(chǎng)數(shù)值分析[M].西安:西安交通大學(xué)出版社,1991.

[10] 吳建華.基于物理模型開(kāi)關(guān)磁阻電機(jī)定子模態(tài)和固有頻率的研究[J].中國(guó)電機(jī)工程學(xué)報(bào),2004,24(8):109-114.

[11] 佟寧澤.大中型感應(yīng)電機(jī)電磁力及定子振動(dòng)分析[D].沈陽(yáng):沈陽(yáng)工業(yè)大學(xué),2006.

Model Analysis of Permanent Magnet Synchronous Motor

LI Ping1MA Yonglong2

(1. Hubei Sanjiang Aerospace Xianfeng Electronic Information Co., Ltd., Wuhan 432000) (2. Navy Representative Office in EO System of Central-South Area, Wuhan 430074)

The paper introduces the theory of the model analysis. The electromechanical analogy method is used to derive the calculation method of the natural frequency of the stator, and the ANSYS software is used to set up motor stator three-dimensional finite element model and model analysis. The natural frequency and vibration mode are calculated to avoid resonance of frequencies and force with electromagnetic force then reduce electromagnetic vibration and noise of PMSM.

permanent magnet synchronous motor, model analysis, ANSYS

2013年8月5日,

2013年9月27日

李娉,女,工程師,研究方向:電子信息、技術(shù)改造等。馬永龍,男,碩士,工程師,研究方向:艦船電子。

TM359.4

10.3969/j.issn1672-9730.2014.02.041