某小型渦噴發動機擴壓輪結構可靠性分析

張 遜，姜年朝，，宋 軍，周光明

（1．總參六十所，江蘇 南京210016；2．南京航空航天大學航空宇航學院，江蘇 南京210016）

0 引言

壓氣機是航空渦噴發動機的重要組成部件，其主要功能是提高流過它的空氣總壓［1－2］。壓氣機一般采用分體式結構，由導風輪和擴壓輪組合而成［3－4］。壓氣機工作時，如果葉片本身強度不夠，產生變形、撓曲或折斷，都將影響發動機的工作性能、安全性能，甚至造成不同程度的故障和飛行事故。因此，壓氣機的葉片強度可靠性計算就非常重要。

壓氣機組件一般都比較昂貴和制作周期較長，通過試驗的方法來確定其可靠性數據不太現實；同時這些關鍵結構所承受的載荷又十分復雜，同類產品之間的可靠性數據往往都不具有可比性。因此，需要對渦噴發動機壓氣機組件結構開展相應的結構可靠性分析，作為可靠性試驗的補充。

在此，基于有限元軟件ANSYS，考慮溫度和離心力的作用，計算擴壓輪的結構強度；采用響應面法，得到擴壓輪的結構可靠性；編制接口程序，實現結構可靠性計算的自動化。

1 擴壓輪有限元分析

組成某無人機用渦噴發動機壓氣機的擴壓輪和導風輪的裝配關系如圖1所示。導風輪為整個壓氣機組件的進口段，考慮到進口空氣中容易吸入顆粒狀硬物，選用高強度合金鋼材料0Cr17Ni4Cu4。氣流通過導風輪之后，在擴壓輪表面形成高速氣流，擴壓輪直徑較大，葉片數較多，材料選為鍛鋁LD7。因為高強度合金鋼的彈性模量遠大于鍛鋁材料的彈性模量，而且導風輪直徑較小、使用的溫度比擴壓輪低，溫度變化小，所以在整個壓葉輪組件中，導風輪的外部環境較溫和；而擴壓輪由于其外形尺寸比導風輪大，材料彈性模量小，一旦承受溫度、離心力等載荷后更容易產生變形或局部應力集中。在整個壓葉輪組件中，擴壓輪部件工作環境最嚴酷，受力后最易變形，其可靠性直接影響壓氣機性能。因此，主要研究壓氣機的擴壓輪結構可靠性。

如圖1所示，擴壓輪采用大小葉片設計，整體是循環對稱模型。為減小計算規模，選取整個擴壓輪的1／13進行網格劃分［5］，采用 ANSYS中的 Solid95單元對擴壓輪進行有限元模型建立。有限元模型如圖2所示。

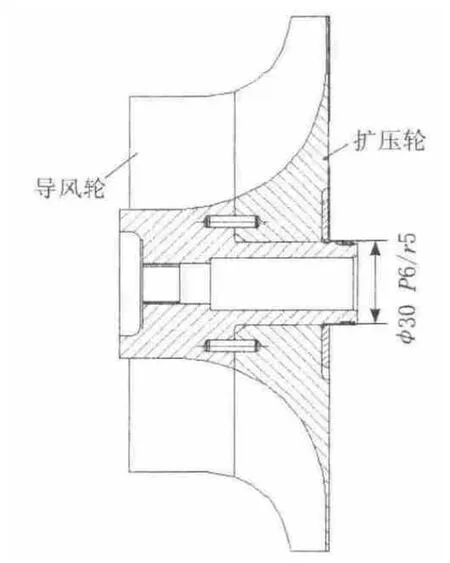
圖1 導風輪和擴壓輪裝配圖

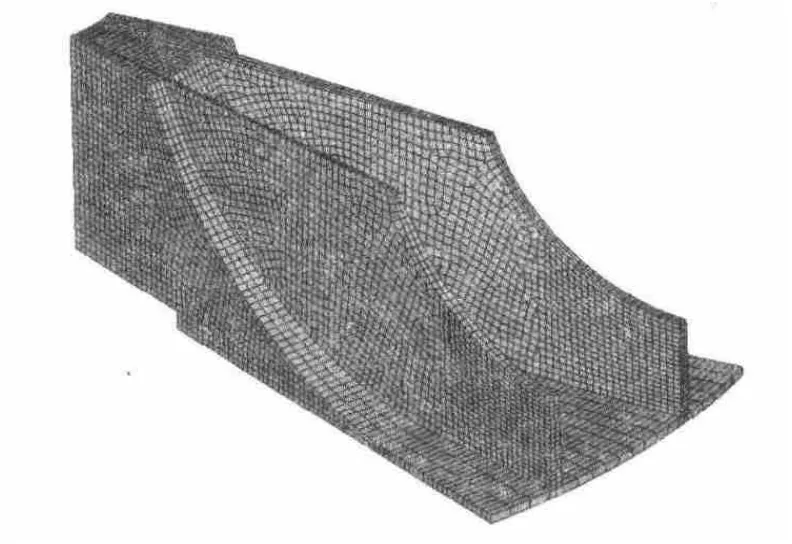
圖2 擴壓輪有限元網格模型（1／13）

渦噴發動機工作時，擴壓輪承受載荷有：葉片本身質量所產生的離心力、通過擴壓輪的氣體流動對葉片產生的氣動力以及葉片受熱不均產生的熱應力［6］。選取發動機地面試車狀態為強度可靠性計算的典型工作狀態，此時，高度為零，無飛行，轉速為最高。由于擴壓輪氣體作用的壓強為0．1～0．2 MPa，量值較小，為突出主要受力影響和簡化問題，計算時忽略了氣動力作用。地面試車時，發動機的冷卻沒有空中飛行時效果好，因此，計算時考慮了熱應力和離心力的耦合作用。考慮熱固邊界絕熱條件下，大小葉尖處溫度最高（214℃），氣流方向轉為水平方向以后溫度梯度上升較快，在擴壓輪葉底部弧度從曲轉直的過程中，擴壓輪表面溫度從57℃上升到127℃左右，溫度分布如圖3所示（57～214℃，整體循環對稱）。擴壓輪材料LD7的性能數據如表1所示。

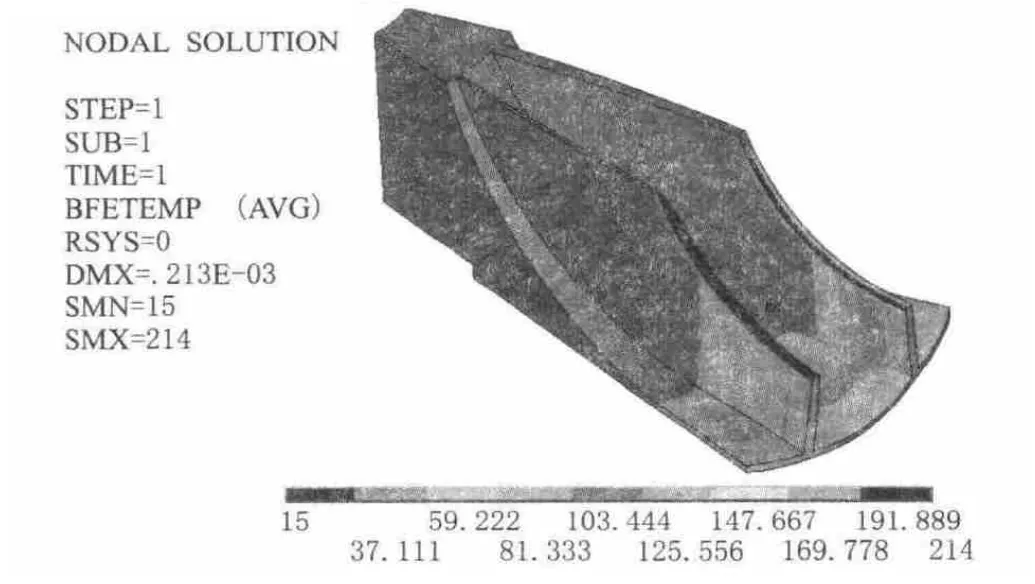
圖3 擴壓輪表面溫度邊界條件

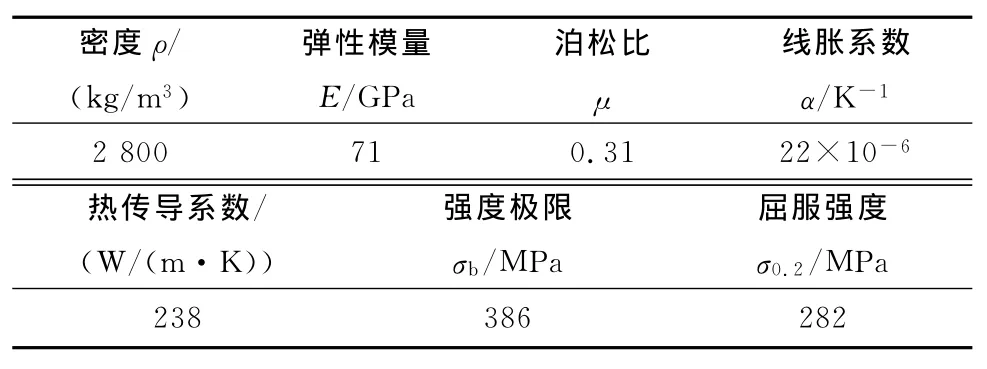
表1 LD7材料性能參數

有限元分析時，對擴壓輪中心裝配孔內表面采用了固定約束（將節點自由度UX，UY，UZ設置為0），同時，對擴壓輪上底面與導風輪接觸的面的節點，約束其UZ方向位移。離心力載荷為輸入轉速49 000 r／min，溫度載荷如圖3所示，計算此時的擴壓輪最大節點應力為312 MPa，最大變形為0．214 mm。有局部區域進入了塑性，其工作狀態下的變形包含有彈性變形和塑性變形，絕大部分變形在室溫下可恢復。

一次計算得到擴壓輪最大等效節點應力和最大變形數據如表2所示，等效應力云圖和最大變形如圖4和圖5所示。

圖4 等效應力云圖

表2 擴壓輪強度計算結果

圖5 變形云圖

2 擴壓輪結構可靠性計算

2．1 可靠性變量

有限元計算時，擴壓輪的幾何尺寸、承受的外載荷和材料性能等都是確定的。實際上，這些參數都是概率意義上的量，是隨機變化的，都影響著擴壓輪的結構可靠性。選取擴壓輪材料的強度極限σs、密度ρ、彈性模量E、泊松比μ、熱傳導系數K、熱膨脹系數α、工作轉速v和溫度載荷T等共8個變量，來計算擴壓輪的結構可靠性。假定所有的變量均服從正態分布，其均值和標準差的確定根據經驗推薦確定。8個隨機變量的均值和標準差如表3所示。

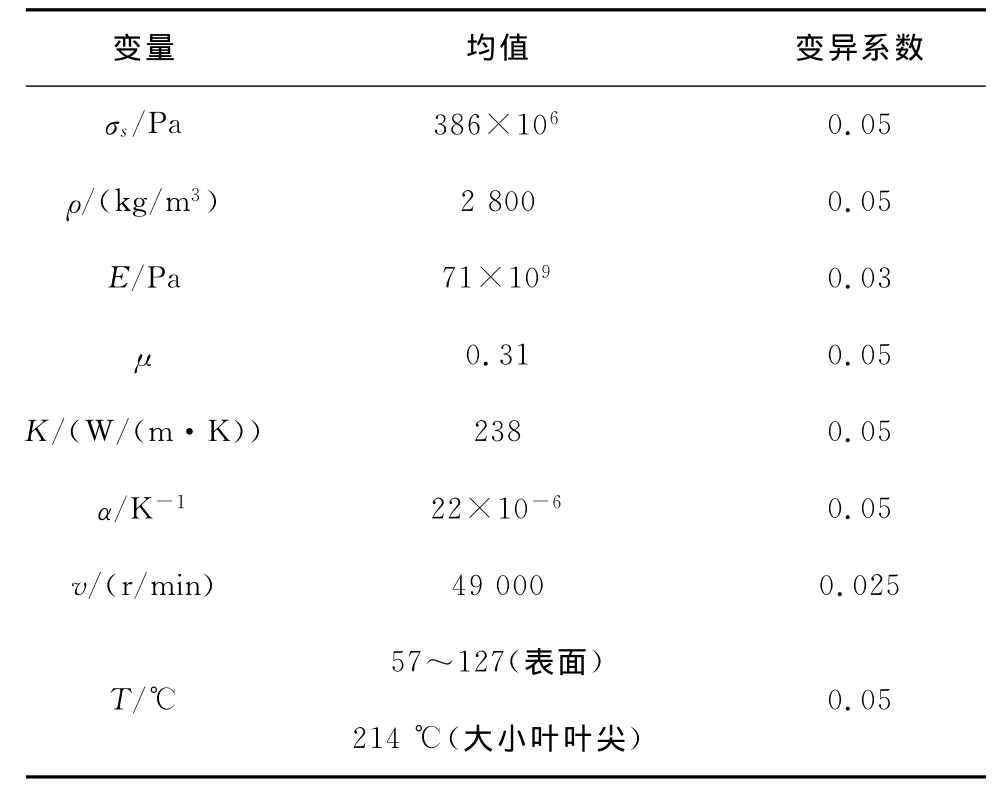
表3 計算變量的分布類型及其參數

2．2 可靠性模型

擴壓輪結構形狀和所承受的載荷復雜，用解析法求擴壓輪的應力很困難。應力－強度干涉模型是分析結構可靠性的基本模型［7－10］，擴壓輪結構可靠性分析采用隱式功能函數，即以擴壓輪上最大的應力不超過使用材料的屈服極限作為判別失效的依據，因此，擴壓輪的結構可靠性功能函數為：

σs為選取材料（LD7）的屈服極限；σmax為擴壓輪的最大等效應力。由于最大等效應力σmax與擴壓輪的尺寸參數以及材料參數之間沒有顯式關系表達式，只能通過有限元軟件計算出它們之間的隱式關系，所以將σmax表示為σmax＝σmax（ρ，E，μ，K，α，v，T），其間的隱式關系由有限元計算軟件ANSYS計算確定。

2．3 可靠性方法選擇

由于每次有限元分析的時間都比較長，而擴壓輪的失效概率比較小，所以無法使用蒙特卡羅法對擴壓輪進行結構可靠性分析（需要調用ANSYS軟件的次數為（102～104）／PF次）。綜合考慮，選取響應面法對擴壓輪進行結構可靠性分析。響應面法如下所述［11－16］：

對于一個階數未知的隱式極限狀態方程，g（x）＝0，x＝（x1，x2，…，xn）為基本隨機向量。傳統的響應面法采用下列不含交叉項的二次多項式（x）來近似g（x），即

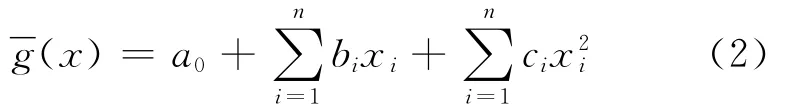
a0，bi，ci（i＝1，2…，n）為（2n＋1）個待定常數。下列2n＋1個以均值點xu＝（u1，u2，…，un）（ui，i＝1，2，…，n為xi的均值）為中心的抽樣點，即

σi為基本變量xi的標準差；f為一個經驗常數，通常取1～3。

由式（3）和式（4）的抽樣點可以首次確定式（2）響應面函數中的2n＋1個待定常數，以上標（1）來表示第1次迭代的結果，則有響應面極限狀態方程為：

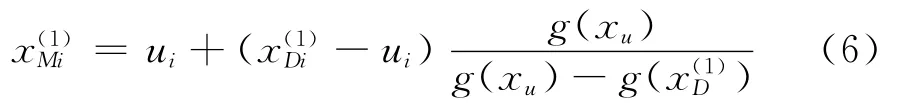
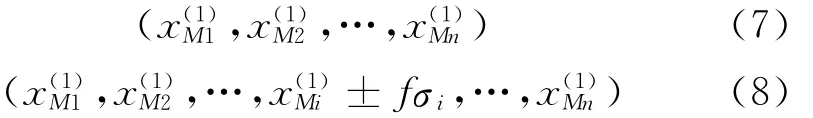
由式（7）和式（8）的抽樣點可以第2次確定式中的待定常數，得到g－（2）（x）＝0及相應的設計點。此迭代過程可以一直進行下去，直到迭代前后2次的設計點距離為止。

3 結果分析

編制接口程序，調用ANSYS軟件，并提取有限元軟件分析的應力，應用響應面方法，計算出擴壓輪的結構可靠性，結果如表4所示。

表4 擴壓輪結構可靠性分析結果

分析結果表明，以超過材料的強度極限為失效準則的時候，擴壓輪結構可靠性比較高，失效概率為3．915 418×10－5，即105件擴壓輪產品大約有4個出現強度失效，能滿足工程實際的需要。

4 結束語

由于計算時忽略了氣動力和葉片振動對擴壓輪強度的影響，溫度載荷也是流場分析的結果，而且所有的變量都假設為正態分布，影響擴壓輪結構可靠性計算的準確度，這些需要進一步完善和研究。但是，基于響應面法，編制接口軟件，調用ANSYS軟件對結構進行可靠性分析的方法，可為計算發動機其他結構可靠性提供借鑒。

［1］ 彭澤琰．航空燃氣輪機原理［M］．北京：國防工業出版社，2000．

［2］ 侯曉春．高性能航空燃氣輪機燃燒技術［M］．北京：國防工業出版社，2002．

［3］ г．C．斯庫巴切夫斯基．航空燃氣渦輪發動機零件結構與計算［M］．北京：國防工業出版社，1992．

［4］ 黃治國，單 鵬，王延榮．微型渦噴發動機結構設計研究［J］．北京航空航天大學學報，2004，30（3）：206－209．

［5］ 姜年朝．ANSYS和 ANSYS／FE－SAFE軟件的工程應用及實例［M］．南京：河海大學出版社，2006．

［6］ 宋兆泓，熊昌炳，鄭光華．航空燃氣渦輪發動機強度設計［M］．北京：北京航空學院出版社，1988．

［7］ 謝里陽，王 正，周金宇，等．機械可靠性基本理論與方法［M］．北京：科學出版社，2009．

［8］ 拓耀飛，李少宏．論結構可靠性的發展［J］．榆林學院學報，2006，16（4）：32－35．

［9］ 黃學明，李國芬．結構可靠性研究綜述［J］．山西建筑，2007，33（11）：76－77．

［10］ 貢金鑫，仲偉秋，趙國藩．結構可靠指標的通用計算方法［J］．計算力學學報，2003，20（1）：12－18．

［11］ 趙 潔，呂震宙．隱式極限狀態方程可靠性分析的加權響應面法［J］．機械強度，2006，28（4）：512－516．

［12］ 王燕萍，呂震宙，岳珠峰．隱式極限狀態方程可靠性研究［J］．應用數學和力學，2005，26（9）：1055－1059．

［13］ 劉成立，呂震宙．結構可靠性分析中考慮高次項修正的組合響應面法［J］．航空學報，2006，27（4）：594－599．

［14］ 呂震宙，楊子政，趙 潔．基于加權線性響應面法的神經網絡可靠性分析方法［J］．航空學報，2006，27（6）：1063－1067．

［15］ 呂震宙，趙 潔，岳珠峰．機械可靠性分析的高精度響應面法［J］．應用數學和力學，2007，28（1）：17－24．

［16］ Romero V J，Swiler L P，Giunta A A．Construction of response surfaces based on progressive－lattice－sampling experimental designs with application touncertainty propagation［J］．Structural Safety，2004，26（2）：201－219．