改進的BP 網絡PID 控制器在無刷直流電機中的應用*

曹 雪，付光杰，牟海維

(1.東北石油大學秦皇島分校 電氣信息工程系，河北 秦皇島 066004;2.東北石油大學a.電氣信息工程學院;b.電子科學學院，黑龍江 大慶 163318)

0 引言

無刷直流電機是電機領域的一個新生代，與傳統的電機裝置進行比較，這種裝置擁有很多的優勢，所以現在已經在實際工業生產過程中得到了大范圍的使用。對于BLDCM 的控制部分而言，它具有控制變量比較多，耦合性能強等特點，并且它的系統變量呈現的并非是線性變化，現代的一些新的控制策略或者相應的控制技術已經開始在BLDCM 的調速過程中得到了驗證。

神經網絡具有非線性映射逼近、分布式信息優化處理、自適應學習等能力，能夠在不明確運行環境的情況下，特別是比較復雜的并且控制變量不能呈現線性變化的，很好地解決一些控制方面的存在的問題，從而使得控制部分魯棒性能增強、擁有適應較高需求的動靜態能力。但是神經網絡學習的缺點是收斂速度過慢，而且容易收斂于局部極小值。

所以本文提出了基于改進的BP 神經網絡PID 控制器的控制理論，并應用在無刷直流電機的調速控制部分，以此來增強裝置調速部分的靜動態能力，從而達到精準性更高、抗干擾信號能力強的穩定安全的控制系統。

1 無刷直流電機的數學模型

(1)電壓方程

根據電機學知識可知，無刷直流電機定子三相繞組電壓方程式為如式(1)所示。

(2)電磁轉矩方程

無刷直流電機的電磁轉矩方程為:

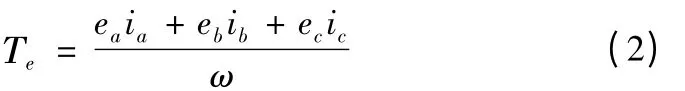
(3)機械運動方程

無刷直流電機的機械運動方程為:

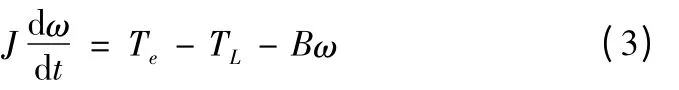
(4)狀態方程

無刷直流電機的狀態方程如下:

無刷直流電機的等效電路圖如圖1 所示。

圖1 無刷直流電機本體的等效電路圖

2 分層調整學習速率的改進BP 算法

BP 算法本質上是梯度下降法，在求取最佳步長的過程中可以看出，增加了網絡的計算量，即計算f(x)的一階導數、一階導數的模和二階導數。為了解決這一問題，本文提出一種分層調整學習速率的改進方法，既改變輸入層與隱含層之間的網絡連接權值的學習速率，又調整隱含層與輸出層之間的網絡連接權值的學習速率。改進方法的基本思想如圖1 所示。

圖2 分層調整學習率的基本思想

設定網絡的學習速率η 為一個較小的值，當滿足f(xk -λkpk)＜f(xk)條件時，則學習速率的改變趨勢為:

如圖2a 中所示，ω* 為ω0的負梯度方向上網絡誤差取得最優值時對應的連接權值，ω0為取得當前網絡誤差值對應的連接權值，ω0按照圖中箭頭方向即負梯度方向運動。當運動到ω1的位置時，ω1處的誤差等值線更接近于誤差最小等值線，所以ω1點對應的誤差值小于ω0點對應的誤差值，則把ω1對應的誤差值賦值給ω0，按照式(5)增大學習速率η，并與連接權值相乘后使得ω0運動到ω2點。ω2點對應的誤差值還是小于ω0點對應的誤差值，繼續把ω2對應的誤差值賦值給ω0，再按照式(5)增大學習速率η，增大后與連接權值相乘后使得ω0運動到ω3點，此時ω3點對應的誤差值大于ω0點對應的誤差值，則終止繼續增大學習速率，認為在ω0點的負梯度方式上的迭代結果為ω2點，而得到的ω2點已經相當靠近ω* 。

這種情況下的學習速率原理如2b 圖所示，ω* 仍為ω0的負梯度方向上網絡誤差最優點。當ω0按照負梯度方向運動到ω1的位置時，ω1點對應的誤差值大于ω0點對應的誤差值，則把ω1對應的誤差值賦值給ω0，按照式(6)減小學習速率η，并與連接權值相乘后使得ω0運動到ω2點。ω2點對應的誤差值小于ω0點對應的誤差值，則終止繼續減小學習速率，認為在ω0點的負梯度方式上的迭代結果為ω2點，而得到的ω2點已經相當靠近ω* 。

3 改進的BP 網絡PID 控制器

BP 網絡的優勢是根據調整網絡連接權值來修正輸出的誤差，通過迭代計算可以極限接近適應度函數，并且由于學習算法易于實現，在神經網絡優化PID 控制中經常采用BP 網絡結構來建立PID 控制器。基于BP 算法的神經網絡可以通過自學習和自適應能力搜索到一組最適合系統性能的PID 參數組合。基于改進的BP 網絡的PID 控制系統結構如圖3 所示，控制器主要由PID 控制器和BP 網絡兩部分構成［2］。

圖3 改進BP 網絡整定參數的PID 控制

BP 網絡通過自學習和自適應能力調節網絡連接權值，盡量使得系統實際輸出值與目標值的差值接近于零，當系統達到最佳性能時，神經網絡輸出值對應KP、KI、KD三個參數。

規定BP 網絡優化PID 控制器的網絡結構是一個3 層網絡，有M個輸入層節點、Q個隱含層節點、3 個輸出層節點。輸出節點的三個輸出值分別對應PID 控制器的三個可調參數KP、KI、KD。隱含層的激發函數可取正負對稱的Sigmoid函數，而輸出層的激發函數為非負的Sigmoid 函數。

網絡輸出層連接權值的學習方法為:

同理可以得到隱含層連接權值的學習算法為:

公式中，g'(x)= g(x)· 1- g(x)，

基于改進的BP 網絡的PID 控制器算法如下:

(1)確定BP 網絡的網絡結構，即確定輸入層節點個數M和隱含層節點個數Q，同時初始化各層的連接權值，對學習速率η 賦值，k =1 ;

(2)采集樣本得到r(k)和y(k)，計算e(k)=r(k)- y(k);

(3)對r(i)，y(i)，u(i -1)e(i)(i = k，k -1，…，k- p)進行統一化處理，作為神經網絡的輸入;

(4)計算神經網絡的各層神經元的輸入和輸出，輸出層的輸出即為PID 控制器的三個可調參數KP(k)、KI(k)、KD(k);

(5)計算PID 控制器的控制輸出u(k)，參與控制和計算;

(6)在網絡的權值都更新一次后，按照(12)計算誤差e(k +1)，如果可以滿足e(k +1)＜e(k)，對其學習速率按照式(5)增大，直到誤差不再減小時停止，則記錄誤差e(k +1)對應的連接權值和如果滿足e(k +1)＞e(k)，對其學習速率按照式(6)減小，直到誤差減小時停止，則記錄誤差對應的連接權值

(7)置k=k+1，返回(2)。

4 改進BP 網絡PID 控制器仿真實驗

假設被控對象為:

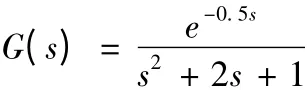
輸入r(k)=1.0 為階躍信號，網絡結構選為三層4-5-3 的結構，即輸入層4 個輸入節點、隱含層5 個節點、輸出層3 個節點。輸入層的4 個輸入分別為系統在k時刻的給定輸入r(k)、輸出y(k)、誤差e(k)=r(k)-y(k)和1，輸出分別為KP、KI、KD三個參數。學習速率η=0.01 ，加權系數初始值取值區間為［-1，1］的隨機數。仿真得到的單位階躍響應曲線和誤差變化曲線如圖4 和圖5 所示。

圖4 單位階躍響應曲線圖

圖5 誤差變化曲線

由于被控對象為二階系統，所以階躍響應曲線呈現衰減正弦振蕩形式。從階躍響應曲線圖和誤差曲線圖可以看出，雖然在剛啟動的時候系統振蕩較大并伴隨較大誤差，但在t=0.2s 左右的時候正弦振蕩明顯衰減，誤差迅速減小，在t=0.3s 時系統運行穩定，誤差趨近于0。從圖中可以看出，改進的BP 網絡在單位階躍響應中的超調量比BP 網絡小，收斂速度更快。由此可以看出，基于改進的BP 算法的神經網絡優化的PID 控制器具有響應速度快、精確性高和穩定性強等特點，通過自學習和自適應能力調節KP、KI、KD三個參數使系統達到最佳性能。本次仿真實驗輸出層輸出值為KP=0.5050、KI=0.5014、KD=0.5009。如圖6 所示。

圖6 輸出層輸出的KP、KI 和KD 的曲線圖

5 改進的BP 算法在無刷直流電機調速控制系統的仿真

在MATLAB 的集成開發環境下［4-5］，利用Simulink提供的豐富仿真模型庫構建出控制系統的仿真模塊。

仿真實驗內容包括加速和加負載兩種情況下進行。在第一種加速情況下:系統空載啟動時額定轉速nref=900r/min，在t=0.2s 時加負載TL=1.5N·m，分別在t=0. 4s、t =0. 6s 和t =0. 8s 加速到nref=1000 r/min、nref=1100r/min 和nref=1200r/min，對改進的BP 網絡PID 控制器進行加速實驗，得到的轉速和轉矩響應曲線如圖7 所示。

從圖中可以看出，轉速的曲線平滑且無超調量，并且在加載負載TL=1.5N·m 的情況下加速轉矩波動小得多，說明本控制系統有較好的跟隨性。

圖7 改進BP 網絡加速時轉速和轉矩反應曲線

在第二種加負載的情況下:系統空載啟動時額定轉速nref= 1000r/min，在t = 0. 2s 時加負載TL= 1 N·m，分別在t =0. 4s 和t =0. 6s 加負載TL=1. 5 N·m和TL=2.0N·m，在t =0.8s 時撤去負載。得到圖8 所示的轉速和轉矩響應曲線。

從圖中可以看出，轉速波動小，本文設計的控制器有很好的帶負載能力。

圖8 改進BP 網絡加負載時轉速和轉矩響應曲線

6 結論

本文從無刷直流電機調速的平穩性和提高帶負載能力方面考慮，設計了改進的BP 網絡的PID 控制器，改進的BP 網絡具有更優秀的學習能力，能夠出色地適應系統的突然變化，建立該控制器的無刷直流電機調速系統，仿真表明，該系統既有較好的快速性和較強的穩定性。

［1］紀志成，薛花，沈艷霞.無刷直流電機調速系統模糊神經網絡控制新方法［J］.電機與控制學報，2003，8(1):5-9，89.

［2］Chang H J，Kim P J，Song D S. Optical image stabilizing system using multirate fuzzy pid controller for mobile device camera［J］.Consumer Electronics，IEEE Transactions on，2009，55(2):

［3］高俊山，牟曉光，楊嘉祥.一種基于遺傳算法和神經網絡的PID 控制［J］.電機與控制學報，2004，8(2):108 -111.

［4］郭宇飛，姚猛. 無刷直流電動機調速的實現［J］. 電機技術，2008(6):8 -10，14.

［5］張琛. 直流無刷電動機原理及應用［M］. 北京:機械工業出版社，2004.