基于PSO-NP 機(jī)械加工尺寸的PI 型廣義預(yù)測(cè)控制*

李國(guó)龍，李國(guó)勇

(太原理工大學(xué) 信息工程學(xué)院，太原030024)

0 引言

機(jī)械加工通過(guò)對(duì)工件的幾何參數(shù)進(jìn)行改造能夠有效的提高社會(huì)生產(chǎn)效率從而產(chǎn)生更大的經(jīng)濟(jì)效益，因此研究機(jī)械加工尺寸的預(yù)測(cè)控制顯得尤為重要。機(jī)械加工過(guò)程中對(duì)加工尺寸進(jìn)行檢測(cè)和控制能夠有效的保證零件加工尺寸的精度，其首要條件是建立適當(dāng)?shù)哪Ｐ蛯?duì)加工尺寸的變化情況進(jìn)行準(zhǔn)確的描述和預(yù)測(cè)，而通過(guò)廣義預(yù)測(cè)控制中的多步預(yù)測(cè)，使系統(tǒng)根據(jù)以往尺寸的輸入，輸出數(shù)據(jù)和已選定的未來(lái)尺寸輸入值，不斷的預(yù)測(cè)未來(lái)尺寸的輸出值從而克服系統(tǒng)的不確定性以及增強(qiáng)系統(tǒng)的魯棒性。但是GPC 中所選的參數(shù)與工程實(shí)際要求的指標(biāo)聯(lián)系不夠緊密，并且對(duì)于隨機(jī)突發(fā)的干擾不能達(dá)到實(shí)時(shí)的控制效果。PI 型廣義預(yù)測(cè)控制能夠有效提高實(shí)時(shí)跟蹤性，改善系統(tǒng)的控制品質(zhì)，結(jié)合兩種控制技術(shù)的優(yōu)勢(shì)可以產(chǎn)生控制效果更加符合實(shí)際要求的PI 型廣義預(yù)測(cè)控制。然而加工過(guò)程中各種因素的機(jī)理非常復(fù)雜，并且加工過(guò)程受到很多實(shí)際條件的約束，在控制系統(tǒng)中存在了約束，勢(shì)必會(huì)對(duì)控制量求解帶來(lái)難度，使問(wèn)題復(fù)雜，計(jì)算量加大，影響了算法的性能，再加之PI 型廣義預(yù)測(cè)控制的比例因子和積分因子整定比較困難，所以對(duì)其參數(shù)整定就有十分重要的意義。文獻(xiàn)［2］利用遺傳算法優(yōu)化整定PI 型廣義預(yù)測(cè)控制的參數(shù)，但并沒(méi)有考慮實(shí)際尺寸加工過(guò)程對(duì)控制作用的約束，文獻(xiàn)［3］在PI 型廣義預(yù)測(cè)控制的基礎(chǔ)上，使用lagrange 乘子法處理PI 型廣義預(yù)測(cè)控制輸入輸出的約束條件，但并沒(méi)有考慮PI 型廣義預(yù)測(cè)控制參數(shù)整定困難的問(wèn)題。本文在PIGPC 算法的基礎(chǔ)上引入MATLAB 最優(yōu)工具箱中求解非線性規(guī)劃問(wèn)題的fmincon 函數(shù)處理機(jī)械加工尺寸過(guò)程中的約束條件，再通過(guò)粒子群算法對(duì)其比例因子和積分因子進(jìn)行優(yōu)化整定，并通過(guò)MATLAB 仿真實(shí)驗(yàn)從而獲得更有效的控制策略，從而提高加工零件的質(zhì)量。

1 加工尺寸的建模和預(yù)測(cè)

1.1 確定目標(biāo)函數(shù)

預(yù)測(cè)控制中的預(yù)測(cè)模型是一個(gè)基礎(chǔ)的模型，主要是被用來(lái)描述系統(tǒng)的動(dòng)態(tài)變化。將通過(guò)在線測(cè)量獲得的加工尺寸數(shù)據(jù)序列作為一個(gè)時(shí)間序列，采用適當(dāng)?shù)脑诰€建模方法建立起相應(yīng)的模型，該預(yù)測(cè)模型能夠根據(jù)系統(tǒng)以往的加工尺寸數(shù)據(jù)預(yù)測(cè)出之后的尺寸數(shù)據(jù)。該預(yù)測(cè)模型將PID 的反饋結(jié)構(gòu)和GPC 的預(yù)測(cè)功能相結(jié)合，其設(shè)計(jì)基于下面的CARMA 模型。

A(z-1)、B(z-1)、C(z-1)分別是na、nb和nc階的z-1的多項(xiàng)式;y(k)、u(k)和ω(k)分別表示尺寸輸出、輸入和噪聲序列;Δ=1- z-1;

式中

PI 型廣義預(yù)測(cè)控制所采用的目標(biāo)函數(shù)為:

其中，{yr(k + j)}是設(shè)定的尺寸輸出值;{y∧(k +j)}為預(yù)測(cè)向前第j步的尺寸預(yù)測(cè)值，Nμ表示輸出控制時(shí)域，輸出的預(yù)測(cè)時(shí)域?yàn)镹y;λ＞0 為控制加權(quán)因子，Kp，Ki為比例因子及積分因子。

在目標(biāo)函數(shù)中加入后一項(xiàng)為了使過(guò)于劇烈的控制增量得到壓制，其目的是為了避免系統(tǒng)超出限制范圍并且抑制劇烈振蕩。

為了獲得尺寸輸出y(k)的向前多步預(yù)測(cè)值，求解如下丟番圖方程:

其中j =1，2，…，N，系數(shù)項(xiàng)Ej、Fj、Gj、Hj都是Z-1的多項(xiàng)式。

由式(1)、(3)可求得k +j時(shí)刻尺寸預(yù)測(cè)值的輸出為:

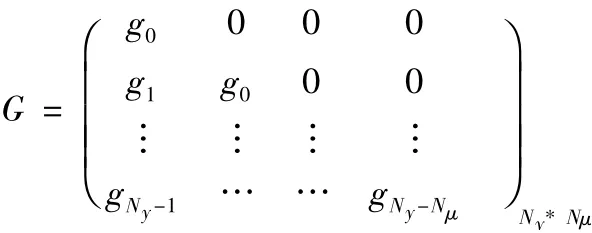
式中，GNy中Z-1項(xiàng)的系數(shù)為gi。

目標(biāo)函數(shù)式(2)的向量形式為:

式(6)中，

1.2 帶約束條件的控制律的求解

1.2.1 控制對(duì)象的約束條件

在實(shí)際生產(chǎn)中對(duì)于尺寸的輸入輸出有一定的限制，一般主要有如下三種約束情況，即控制增量約束，控制量約束和輸出約束。

控制量增量約束:

控制量幅值約束:

輸出量約束:

上式中，

帶約束條件的PI 型廣義預(yù)測(cè)控制問(wèn)題，可以歸結(jié)為在滿足(7)，(8)，(9)三個(gè)約束條件下，使目標(biāo)函數(shù)(6)達(dá)到最小。

1.2.2 非線性規(guī)劃

非線性規(guī)劃中的目標(biāo)函數(shù)和約束條件至少有一個(gè)是未知量的非線性函數(shù)，其主要研究一個(gè)n元實(shí)函數(shù)在一組等式或不等式的約束條件下的極值問(wèn)題。因此上述問(wèn)題可以轉(zhuǎn)化為求解非線性規(guī)劃問(wèn)題進(jìn)而求得目標(biāo)函數(shù)(6)在約束條件下的最小值，進(jìn)而求得帶約束的PI 型廣義預(yù)測(cè)控制的控制律。

非線性規(guī)劃的形式可以表達(dá)如下:

其中，設(shè)計(jì)變量x =［x1，x2，…xn］T是n維歐式空間Rn的向量，f(x)為(6)式中的目標(biāo)函數(shù)，hi(x)=0，gj(x)≤0 為式(7)，(8)，(9)的約束條件。

求解該非線性規(guī)劃問(wèn)題，通過(guò)使用MATLAB 最優(yōu)化工具箱中的fmincon 函數(shù)，其搜索在約束條件下非線性多元函數(shù)的最小值是從一個(gè)預(yù)估值開(kāi)始的。其形式可以表示如下:

上式中，x、b、beq、lb和ub是矢量;A和Aeq為矩陣;c(x)和cep(x)返回矢量的函數(shù);f(x)、c(x)和cep(x)是非線性函數(shù)。

2 基于粒子群算法的約束PI 型廣義預(yù)測(cè)控制參數(shù)整定

帶約束的PI 型廣義預(yù)測(cè)控制存在著比例因子、積分因子整定的困難，所以對(duì)其參數(shù)優(yōu)化整定顯得非常重要，在計(jì)算智能領(lǐng)域，粒子群算法是一種針對(duì)群體的智能優(yōu)化算法。該算法通過(guò)個(gè)體之間的協(xié)作來(lái)尋找最優(yōu)解的進(jìn)化計(jì)算技術(shù)，用于解決復(fù)雜系統(tǒng)的優(yōu)化問(wèn)題，算法簡(jiǎn)單且容易實(shí)現(xiàn)。該算法最早是在1995 年由Kennedy 和Ebennedy 共同提出的，其主要是根據(jù)人工生命和演化計(jì)算理論。PSO 算法是通過(guò)觀察鳥(niǎo)類(lèi)的捕食行為發(fā)現(xiàn)，鳥(niǎo)通過(guò)跟蹤其周?chē)邢迶?shù)量的同伴從而使整個(gè)鳥(niǎo)的群體保持在一個(gè)中心控制范圍中，其表明簡(jiǎn)單規(guī)則的相互作用可以引起復(fù)雜的全局行為。鳥(niǎo)類(lèi)只有在離食物最近的鳥(niǎo)的附近范圍內(nèi)尋找才能最快速的找到食物。PSO 算法就是根據(jù)鳥(niǎo)類(lèi)尋找食物的方法得到的啟發(fā)，依次來(lái)解決求解最優(yōu)解的問(wèn)題，算法中每個(gè)粒子都有可能解決這個(gè)問(wèn)題，并且每個(gè)粒子的適應(yīng)度值都是由適應(yīng)度函數(shù)決定的。其中粒子的速度決定粒子的距離和移動(dòng)方向的，根據(jù)其他粒子的移動(dòng)經(jīng)驗(yàn)該速度不斷的進(jìn)行動(dòng)態(tài)的調(diào)整，從而使個(gè)體粒子在整個(gè)可解空間中尋求到最優(yōu)解。

粒子群算法初始化的一群粒子中每個(gè)粒子的特征是用位置，速度和適應(yīng)度值三個(gè)指標(biāo)表示的，粒子的優(yōu)劣是由適應(yīng)度值的好壞決定的，適應(yīng)度值的求解是通過(guò)計(jì)算適應(yīng)度函數(shù)得到的。空間中粒子的運(yùn)動(dòng)，更新個(gè)體極值位置時(shí)取決于個(gè)體極值Pbest和群體極值Gbest。個(gè)體極值Pbest表示個(gè)體有經(jīng)歷的所有位置中最優(yōu)的那個(gè)位置。粒子每變化一次位置要通過(guò)適應(yīng)度函數(shù)計(jì)算一次該位置的適應(yīng)度值，而為了獲得個(gè)體極值Pbest及群體極值Gbest的位置，可以通過(guò)將新粒子的適應(yīng)度值和個(gè)體極值，群體極值的適應(yīng)度值做比較得出。粒子就是根據(jù)這兩個(gè)極值不斷更新自己的速度和位置。

式中，w為慣性權(quán)重;d =1，2…，D;D表示一個(gè)粒子的總維數(shù)，根據(jù)具體的優(yōu)化問(wèn)題而定;i =1，2，…，n;n表示粒子的總個(gè)數(shù);n為當(dāng)前迭代次數(shù);Vid為粒子的速度;c1，c2是非負(fù)的常數(shù)，稱為加速度因子;r1，r2是分布于［0，1］區(qū)間的隨機(jī)數(shù)。為降低粒子搜索的盲目性，一般將其位置和速度限制在一定的區(qū)間［- Xmax，Xmax］。

2.1 慣性權(quán)重的選取

慣性權(quán)重體現(xiàn)的是粒子繼承先前速度的能力，Shi.Y 指出較大的慣性權(quán)值能夠獲得較好的全局搜索能力，而要想獲得較好的局部搜索則需要較小的慣性權(quán)值［8］。為了使算法同時(shí)具有較強(qiáng)的局部搜索能力和全局搜索能力，線性遞減慣性權(quán)重被提出，即:

其中，初始慣性權(quán)重為wstart;wend為迭代至最大次數(shù)時(shí)的慣性權(quán)重;k為當(dāng)前迭代代數(shù);Tmax為最大迭代代數(shù)。通常而言，慣性權(quán)值wstart =0.9 ，wend =0.4 時(shí)算法性能最好。這樣，隨著迭代的進(jìn)行，慣性權(quán)重由0.9 逐漸遞減至0.4，迭代初期較大的慣性權(quán)重是為了使算法的全局搜索能力較強(qiáng)，為了獲得更加精確的局部搜索能力可以使迭代后期的慣性權(quán)重較小。

2.2 適應(yīng)度函數(shù)的選取

應(yīng)用粒子群算法整定帶約束條件的PI 型廣義預(yù)測(cè)控制問(wèn)題歸根到底是一個(gè)優(yōu)化問(wèn)題，是通過(guò)求Kp，Ki從而求得目標(biāo)函數(shù)(6)的最小值，故采用目標(biāo)函數(shù)(6)做為PSO 算法的適應(yīng)度函數(shù)。

2.3 參數(shù)整定的算法實(shí)現(xiàn)

PI 型廣義預(yù)測(cè)控制在實(shí)際應(yīng)用中存在著復(fù)雜多樣的約束條件，只有當(dāng)目標(biāo)函數(shù)可微時(shí)，才能求解約束的二次規(guī)劃，且只能獲得局部最優(yōu)解。而PSO 算法不要求目標(biāo)函數(shù)以及約束條件可微，便能快速的求得全局最優(yōu)解，所以將PSO 算法與具有PI 廣義預(yù)測(cè)控制相互結(jié)合，能夠很好的解決在約束條件下被控對(duì)象很難獲得準(zhǔn)確參數(shù)以及收斂速度慢的問(wèn)題。

粒子群算法整定帶約束的PI 型廣義預(yù)測(cè)控制的比例因子、積分因子算法如下:選取性能指標(biāo)式(6)為PSO 算法的適配值評(píng)價(jià)函數(shù);比例，積分因子Kp，Ki可認(rèn)為是PSO 算法的尋優(yōu)目標(biāo);粒子的種群為待求解的集合;根據(jù)PSO 算法的原理，首先初始化粒子的位置和速度，評(píng)價(jià)每個(gè)粒子的適配值，得到個(gè)體最優(yōu)值Pbest和種群的最優(yōu)值Gbest和此時(shí)粒子的位置，利用式(10)、(11)對(duì)粒子位置Xt和慣性權(quán)值w進(jìn)行迭代更新，并重新計(jì)算每個(gè)粒子的適配度值。如果滿足算法的結(jié)束條件，具有最小適配值的粒子的位置就是所要求最佳Kp，Ki。

該算法的流程圖如下:

圖1 PSO 算法優(yōu)化參數(shù)流程圖

3 基于PSO-NP 機(jī)械加工尺寸的PI 型廣義預(yù)測(cè)控制

首先獲得m(視具體情況取值)個(gè)加工尺寸檢測(cè)數(shù)據(jù)，，加工開(kāi)始后對(duì)式(3)中的參數(shù)進(jìn)行非線性最小二乘估計(jì)，然后按式(4)求取y∧(k +j)，之后每增加一個(gè)數(shù)據(jù)，進(jìn)行一次上述過(guò)程，從而得到各時(shí)刻超前j步預(yù)測(cè)的加工尺寸數(shù)據(jù)序列;當(dāng)所得的數(shù)據(jù)量達(dá)到m(視具體情況取值)時(shí)，每次新得一個(gè)尺寸數(shù)據(jù)就丟棄一個(gè)最老的數(shù)據(jù)，使在線預(yù)測(cè)的數(shù)據(jù)量始終為m。為了將控制性能的指標(biāo)達(dá)到最優(yōu)，通過(guò)非線性規(guī)劃處理機(jī)械尺寸預(yù)測(cè)過(guò)程中輸入輸出的約束條件，再通過(guò)粒子群算法對(duì)該算法中的參數(shù)Kp，Ki進(jìn)行優(yōu)化整定。其整個(gè)算法的流程圖如下:

圖2 PSO-NP 優(yōu)化PI 型廣義預(yù)測(cè)控制

4 仿真研究

選取仿真的機(jī)械加工系統(tǒng)為:y(k)=0.3y(k -2)+0.3y(k -2)u(k -2)+0.5u(k -1)，帶約束的廣義PI 廣義預(yù)測(cè)控制的預(yù)測(cè)長(zhǎng)度Ny =3，控制長(zhǎng)度Nu =2，控制加權(quán)系數(shù)λ=1，初始比例、積分因子Kp =9，Ki =3，設(shè)置對(duì)象的輸入輸出為的約束為-0.3 ≤Δu(k)≤0.3，-1≤u(k)≤1，0 ≤y(t)≤2.5;粒子群算法整定Kp，Ki，學(xué)習(xí)因子c1= c2=2，慣性權(quán)重根據(jù)式(12)確定。

仿真結(jié)果如下:

圖3 PSOPIGPC 與GAPIGPC 優(yōu)化參數(shù)后對(duì)比輸出

圖4 未對(duì)算法中參數(shù)進(jìn)行優(yōu)化整定的仿真

圖5 對(duì)參數(shù)進(jìn)行優(yōu)化整定后的本文算法仿真

通過(guò)圖3 的仿真結(jié)果可以看出，用粒子群算法取代文獻(xiàn)［2］中的遺傳算法優(yōu)化參數(shù)，可以有效減少系統(tǒng)的超調(diào)，縮短調(diào)整時(shí)間，從而達(dá)到更好的控制效果。通過(guò)圖4 和圖5 中輸出量跟蹤曲線的比較可以看出，本文算法相比于文獻(xiàn)［3］中未對(duì)參數(shù)進(jìn)行優(yōu)化的算法具有更好的跟蹤性能和適應(yīng)能力，輸出的波動(dòng)更小，通過(guò)圖4，圖5 中控制量曲線的對(duì)比，對(duì)帶約束的PI 型廣義預(yù)測(cè)的參數(shù)進(jìn)行優(yōu)化整定后，控制量變化更加緩和并且減少了因模型失配引起的控制量振蕩。

5 結(jié)束語(yǔ)

本文將工程中廣泛應(yīng)用的PI 控制技術(shù)與廣義預(yù)測(cè)相結(jié)合應(yīng)用到機(jī)械尺寸加工過(guò)程中，通過(guò)粒子群算法對(duì)其進(jìn)行參數(shù)的優(yōu)化整定從而達(dá)到良好的控制效果，通過(guò)仿真可以看出本文算法能夠更加保證零件的加工質(zhì)量，且本文算法策略便于實(shí)施，可應(yīng)用于數(shù)控機(jī)床或自動(dòng)化生產(chǎn)線上。

［1］李國(guó)勇. 智能預(yù)測(cè)控制及其MATLAB 實(shí)現(xiàn)(第2 版)［M］.北京:電子工業(yè)出版社，2010.

［2］仉寶玉.肖軍.基于GA 參數(shù)優(yōu)化整定的PI 型廣義預(yù)測(cè)控制［J］.科學(xué)技術(shù)與工程，2011，11(2):367 -370.

［3］滕達(dá)，于佐軍，趙繼偉.帶約束的PI 型廣義預(yù)測(cè)控制［J］.青島科技大學(xué)學(xué)報(bào)，2012，33(5):495 -499.

［4］陳進(jìn)東，王鮮芳，潘豐. 基于PSO 滾動(dòng)優(yōu)化的LS-SVM 預(yù)測(cè)控制［D］. 無(wú)錫:江南大學(xué)，2009.

［5］李明.詳解MATLAB 在最優(yōu)化計(jì)算中的應(yīng)用［M］.北京:電子工業(yè)出版社，2011.

［6］張強(qiáng)，李少遠(yuǎn).基于遺傳算法的約束廣義預(yù)測(cè)控制［J］.上海交通大學(xué)學(xué)報(bào)，2004，38(9):1562 -1566.

［7］楊春，李國(guó)勇.基于RBF 神經(jīng)網(wǎng)絡(luò)的PI 型廣義預(yù)測(cè)控制［D］.中國(guó)科技論文在線，2013.

［8］徐青鶴，劉士榮，呂強(qiáng). 一種改進(jìn)的粒子群算法［D］. 杭州:杭州電子科技大學(xué)自動(dòng)化研究所，2008.

［9］李旭芳，王士同. 一種自適應(yīng)粒子群算法［D］. 無(wú)錫:江南大學(xué)，2009.

［10］龔立雄，萬(wàn)勇，侯智，等.基于雙隱曾L-M 算法的BP 神經(jīng)網(wǎng)絡(luò)機(jī)械加工誤差預(yù)測(cè)控制模型［D］. 重慶:重慶理工大學(xué)，2013.