面向綠色制造的刀具評價方案的研究*

牛印寶，汪永超，王 宇

(四川大學 制造科學與工程學院，成都 610065)

0 引言

在機械制造系統中，刀具占有很重要的地位，它不僅影響著產品的加工質量、生產效率以及加工成本，同時還影響著產品加工過程中能源的消耗、粉塵的產生、噪聲的產生、使用的安全性以及切削液污染等，也就是影響著刀具的綠色性。刀具的合理選用已成為綠色制造的關鍵所在，對刀具評價方案的研究顯得尤為重要。

目前對產品評價的方法有很多種，一般包括層次分析法、灰度關聯分析法、模糊評價法、模糊層次法等。這些方法在一些領域已經取得了一些成果，例如章毅使用層次分析法對瀝青路面的施工質量進行評價［1］、沈強等使用灰色多層次判斷模型對生物質能開發方案進行評價［2］、丁麗宏則把灰度關聯分析法和層次分析法相結合起來對邊坡的穩定性進行評價［3］、王新民等人用層次分析法和可拓學模型對巖質邊坡穩定性進行評價［4］、王桂萍等人則使用模糊可拓層次分析法對數控機床的綠色度進行評價［5］，這些方法都有他們的優點和缺點。但是這些方法在刀具上運用的比較少，在這方面做過研究的是譚顯春等人的利用模糊聚類綜合評價法對刀具進行評價［6］但是這種方法過于單一，而且不能進行單指標的比較。

本文在前人的基礎上吸取他們優點并結合層次分析法中幾種標度的比較［7］，在綠色制造的前提下提出了以en/5為標度的改進的層次分析法，結合模糊綜合評價法對刀具進行評價。這種方法可以解決以下問題:判斷刀具是否是綠色的;刀具綜合評價的綠色度是多少;刀具單指標綠色度是多少;當刀具總得分相近時可根據單指標和企業喜好進行選擇;可以對刀具進行改進。

1 刀具評價體系的建立

刀具的評價是一個多因素、多層次的綜合評價問題。傳統的刀具選擇往往強調加工質量、加工時間和加工成本而忽略了能源的消耗和對環境的影響，這顯然是不符合綠色制造的要求的。對于綠色制造企業來說刀具選擇時最理想的狀態是要求加工時間最短、加工質量最好、加工成本最低(可以是單價加工成本)、資源消耗最少以及對環境的影響最弱。但是事實上這幾種因素它們之間相互影響相互制約很難同時滿足理想狀態的要求，只能根據側重點的不同對它們進行一個綜合的評價。本文就從這5 個方面出發以它們作為指標建立了刀具的綜合評價體系，如圖1 所示。由于各評價指標又包含了很多子因素集所以還可以繼續進行劃分，比如加工時間指標可以劃分為輔助時間和切削時間兩個子指標。

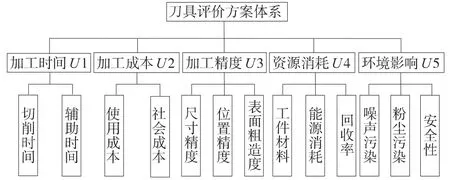
圖1 刀具綜合評價體系

2 改進的層次分析法

層次分析法(AHP:Analytic Hierarchy Process)是由美國著名運籌學家T.L.Saaty 教授提出來的一種系統分析方法。這種方法把一個復雜的問題按屬性的邏輯關系逐層分解，形成一個層次結構來加以分析，以簡化分析問題的難度，并在逐層分解的基礎上加以綜合，給出復雜問題的求解結果［8］。本文采用的是改進了的層次分析法，具體的分析步驟如下。

2.1 判斷矩陣的建立

在傳統的層次分析法中，判斷矩陣建立的時候多采用的是1～9 標度，這種標度雖然簡單明了，標度均勻性很好，但是一致性很差，這就給判斷矩的建立帶來了麻煩。若一致性不滿足就要從新確立判斷矩陣，直到滿足為止，這不僅有很大的盲目性而且可能限制參與評定判斷矩陣的專家的真實想法，造成結果不準確［9］。一般情況下對判斷矩陣有三種評估的準則，即一致性指標、最大偏差值和均方差，它們的取值都是越小越好，根據這三種評估準則我們就可以判斷出那種標度較好。本文通過對文獻［7］和文獻［9］的學習決定采用en/5標度來代替1～9 標度，具體的證明過程可以參考上面兩個文獻。這兩種標度定義如下表所示，我們可以進行一下對比。

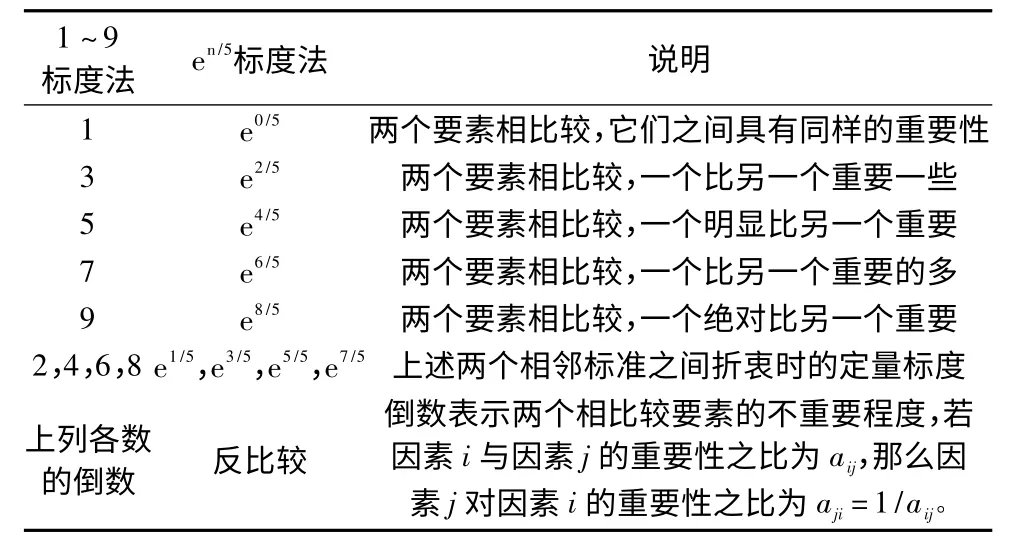
表1 標度定義

2.2 層次單排序

判斷矩陣是針對上一層要素而言，進行兩兩比較的重要性評比數據。層次單排序就是把本層所有要素針對上一層某要素來說，排出評比的優劣次序，這種次序以相對數值的大小表示出來，成為相對權重向量。層次單排序的計算過程可以歸結為求判斷矩陣的最大特征值和其所對應的特征向量。傳統的算法在計算過程中為了避免龐大的計算過程而多采用近似計算的方法，常用的有“方根法”和“求和法”。事實上我們可以借助MATLAB 工具中的eig()函數可以很快的計算出判斷矩陣的最大特征值和所對應的特征向量。最大特征值用來判斷矩陣的一致性指標，而其對應的特征向量則對應這幾種因素的相對重要程度，將它們進行歸一化后就能得到每一個因素對應的相對權重。

假設指標層要素U1，U2，…，Un，所對應的判斷矩陣的最大特征值是λmax，最大特征值對應的特征向量為M=［m1，m2，…，mn］T，那么此指標層的相對權重向量為W=［w1，w2，…，wn］T，W 和M 滿足如下的公式:

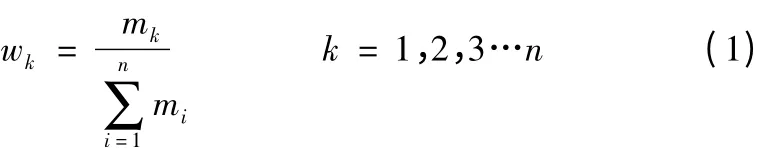
2.3 一致性檢驗

一致性是指判斷矩陣中各要素的重要性判斷是否一致，不能出現矛盾。只有滿足了一致性的條件上述的權重向量才有用，否則就需要重新設置判斷矩陣。滿足完全一致性的條件是判斷矩陣的akj = akl/ajl，但是事實上人們在進行主觀判斷時對系統評價方案的認識具有片面性，所建立的判斷矩陣很難滿足完全一致性。此時我們引入判斷矩陣的一致性指標，來檢驗人們思維判斷的一致程度。一致性指標記為C.I.，計算公式如下:

為了度量不同階判斷矩陣是否具有滿意的一致性，再次引入判斷矩陣平均一致性指標R.I.。我們把C.I.和R.I.的比值稱為隨機一致性比值［10］，公式如下:

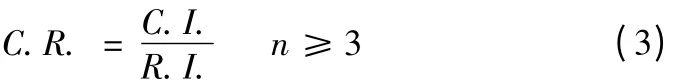
當矩陣是一階或者是二階時肯定具有滿意的一致性，不用利用上述公式就可判斷。對于3 階以上的矩陣只要滿足C.R.＜0.1，我們就可以認為該矩陣具有滿意的一致性，其中R. I.的值和判斷矩陣的階數有關，具體關系如表2 所示。

表2 平均隨機一致性指標

2.4 層次總排序

所謂的層次總排序就是對于目標層而言，本層次各要素重要程度的次序排列。假設上一層要素U1，U2，…，Um的總排序已經確定，其數值為w1，w2，…，wm;且本層各要素A1，A2，…，An對Ui的層次單排序結果為，如果設本層的總排序為M=［m1，m2，…，mn］T那么M 的元素mj滿足如下的公式:

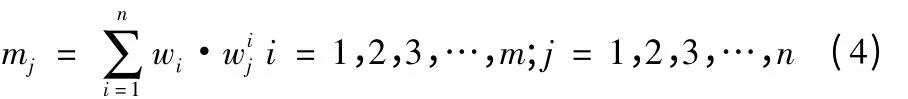
3 模糊綜合評價法

3.1 評價模型的選擇

模糊評價模型包括評價因素集、評價指標集、因素權重集和單因素評價四個要素。如果我們把U=［u1，u2，…，um］作為評價因素集，把E =［e1，e2，…，eg］作為評價等級集。那么在評價因素集和評價質量集之間的模糊關系就可以用模糊矩陣R 表示出來［11］，如下公式:

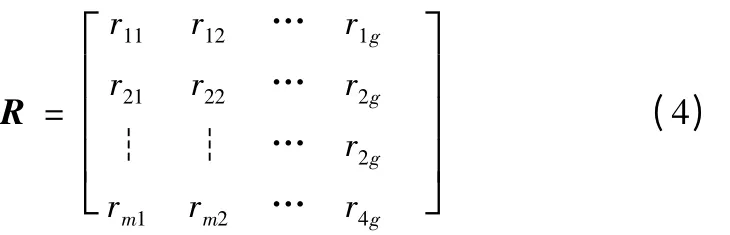
其中:rij表示評價因素ui相對于上層因素U 來說對評價等級集ej的隸屬度，且rij滿足0≤rij≤1。

假設U=［u1，u2，…，um］中ui相對于U 的權重集(層次單排序)為W=［w1，w2，…，wn］T那么因素U的評價矩陣V 有如下公式:

一般情況下一個評價因素集有很多層，如果ui是U 的下層因素而ui本身沒有下層因素那么我們就可以稱V 是U 的單因素評價矩陣，事實上U 的評價矩陣確定后如果還有上層因素，則可以和它同層次的因素重新組成更高一層的模糊矩陣，以此類推就可以求出目標層的最終的評價矩陣。求最終的評價矩陣還有另外一種方法就是把先算出各個基層要素的層次總排序設為MZ，然后再得到基層各要素組成的模糊判斷矩陣RZ，那么最終的評價矩陣VZ可以用下面的公式表示:

3.2 計算綜合評價分數

為了更直觀的對刀具進行評價，我們以一定的分數表示出刀具的評價結果，此時根據越大越好的原則［12］可以選擇評價集E=［很好，好，一般，差，很差］并把它們附上相應的分值為E=［100，80，60，40，20］規定得分為60 分以上的為綠色刀具，那么各級指標的綜合評價得分是:

4 實例分析

某機床廠的切削加工過程中使用的刀具是傳統的普通高速鋼，現進口了一種TiN 涂層高速鋼刀具，該廠家想知道進口的刀具是不是綠色的以及綠色度有多大，除此外廠家還想知道進口刀具比傳統刀具優越性主要體現在哪些方面。為此本文使用上述方法對刀具進行評價。

本文使兩種刀具分別在相同的條件下對工件進行加工，然后請10 位專家按照評價集對它們進行評價以確定模糊矩陣，結合指標權重對兩種刀具進行單指標評價。各指標的權重如表3 所示。

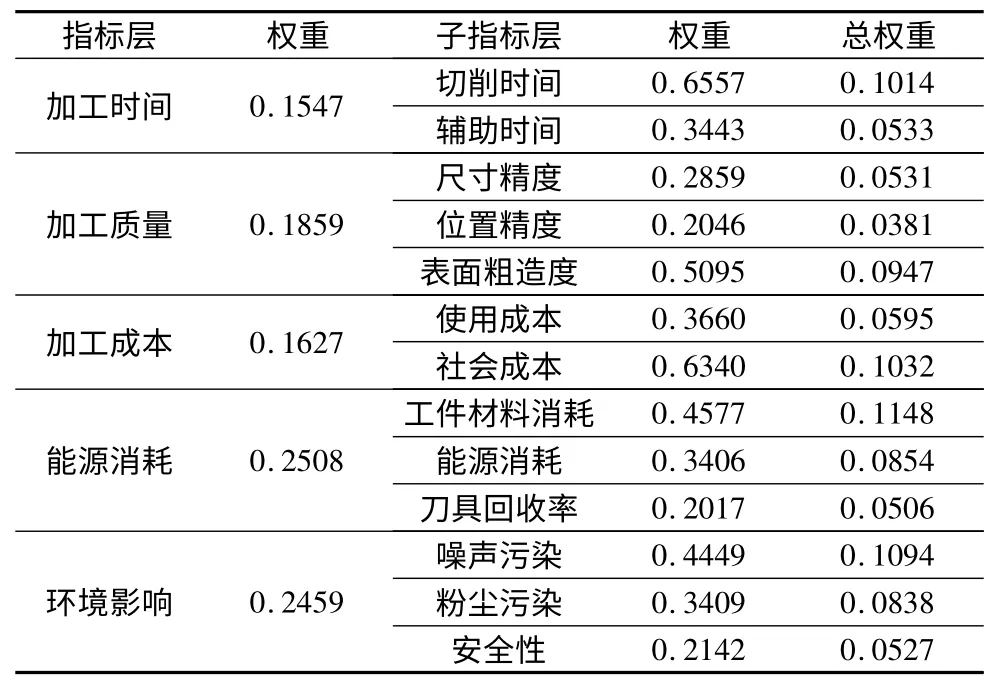
表3 指標權重

對于模糊判斷矩陣的建立，在表中我們已經做了隸屬度的處理，結果如表4 所示。

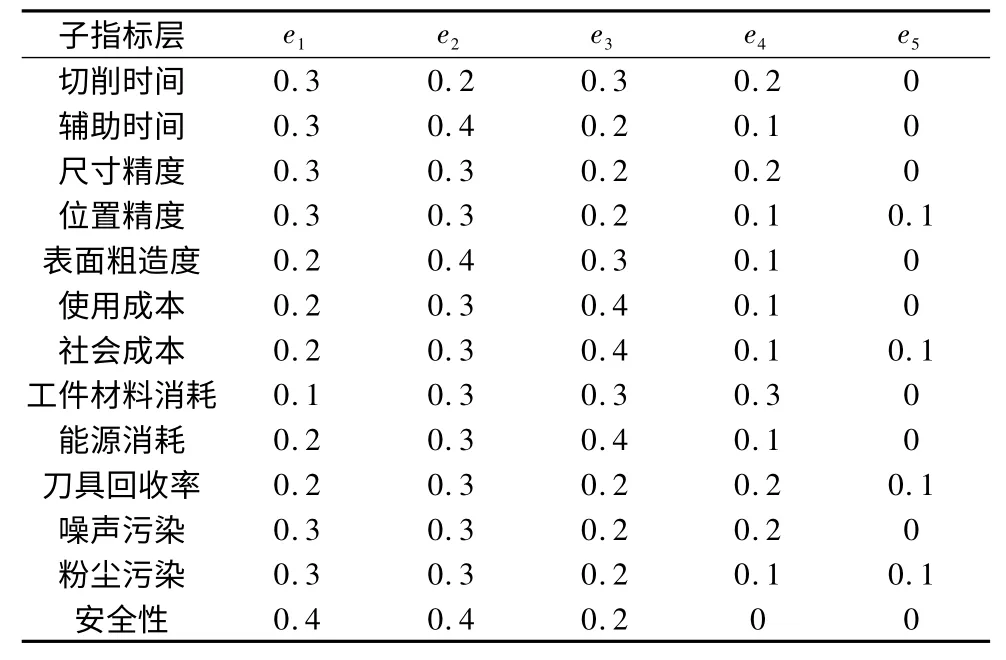
表4 進口TiN 涂層刀具評價數據

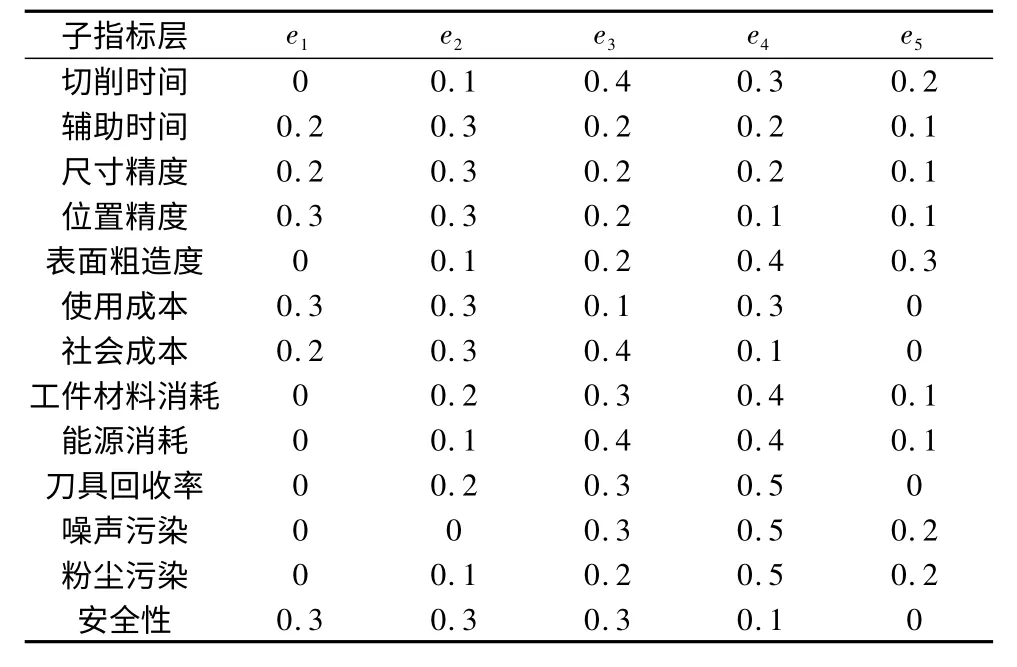
表5 傳統刀具評價數據

在上表中我們以進口TiN 涂層刀具的加工時間為例進行單因素的評價，由表3 和表4 我們知道加工時間對應的兩個子指標的權重為和對應的模糊矩陣如下:

由此我們可以得到單因素的評價矩陣為:

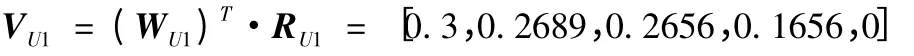
由公式7 可以得到評價分數F=74.0658.

用同樣的方法我們可以得到其它單因素的評價矩陣和評價分數如下:

傳統刀具各因素評價矩陣和分數如下

上述單指標評價矩陣和評價分數計算出來后，我們來對他們進行綜合的比較，即計算它們的綜合評價矩陣和綜合評價得分，計算綜合評價矩陣的方法有上面提到的兩種，下面以進口TiN 涂層刀具為例使用第一種方法進行計算。

按照第一種方法，綜合評價的模糊矩陣由單因素指標評價矩陣組成，如下公式:

而綜合評價的權重值則可由表3 得到:W=

那么綜合評價矩陣可以表示為

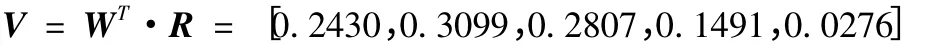
綜合評價分數F =E·VT =72.4496 。

使用同樣的方法可以得到傳統刀具的評價矩陣和綜合評價分數如下:

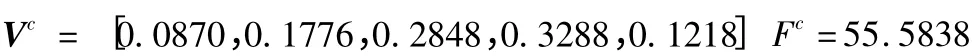
通過上述兩個刀具的綜合評價我們可以看出，進口的TiN 涂層刀具得分是72.4496 屬于綠色刀具，而且綠色度中等偏上，傳統的刀具得分55.5838 不屬于綠色道具。從單因素評價我們可以看出雖然進口的TiN 涂層刀具和傳統的刀具成本基本相同，但是其他方面要比傳統刀具優越的多，因此選擇進口的TiN 涂層刀具是符合綠色制造要求的。

5 結論

刀具的選擇是綠色制造的關鍵，對刀具進行評價對于制造業來說是十分重要的事情。通過以加工質量、加工時間、加工成本、能源消耗和環境影響為指標采用層次分析法和模糊綜合評價法對刀具進行評價，結合實例說明了該方法是可行的和實用的。事實上這種方法還能對刀具進行其他方面的評價，上述實例中雖然進口TiN 涂層刀具是綠色刀具，評價總得分是72.4496，但是能源消耗方面得分只有67.1282 低于總得分，因此在能源消耗方面有待改進。此外，如果機床加工廠有兩種刀具使用上述方法得到的評價總得分相似，無法進行選擇時，我們可以根據單因素得分進行選擇，假設此加工廠對環境影響方面比較看重，那么可以選擇環境影響得分較高的刀具。此評價方案的計算過程全部在Matlab 中進行，簡單而且快捷，能夠準確快速的對刀具進行評價。

［1］章毅，李立寒.基于層次分析法的瀝青路面施工質量評價模型［J］.同濟大學學報(自然科學版)，2011，39(2):253-258.

［2］沈強，姚炎明，何勇. 基于灰色多層次綜合評判模型的生物質能開發方案優選［J］.農業工程學報，2012，28(17):179 -185.

［3］丁麗宏.基于改進的灰關聯分析和層次分析法的邊坡穩定性研究［J］.巖土力學，2011，32(11):3437 -3441.

［4］王新民，康虔，秦健春，等.基于層次分析法—可拓學模型在巖質邊坡穩定性安全評估中的應用［J］. 中南大學學報(自然科學版)，2013，44(6):2455 -2462.

［5］王桂萍，賈亞洲，周廣文. 基于模糊可拓層次分析法的數控機床綠色度評價方法及應用［J］.機械工程學報，2010，46(3):142 -147.

［6］譚顯春，劉飛，曹華軍，等.面向綠色制造的刀具選擇決策模型及其應用［J］.重慶大學學報，2003，26(3):117-121.

［7］駱正清，楊善林.層次分析法中幾種標度的比較［J］.系統工程理論與實踐，2004，24(9):51 -60.

［8］謝家平.綠色設計評價與優化［M］.武漢:中國地質大學出版社，2004.

［9］孫東升，朱懿，周水興. 基于指數標度的層次分析法在橋梁評定中的應用［J］.重慶交通大學學報(自然科學版)，2010，29(6):867 -870.

［10］Metin Dagdeviren，Serkan Yavuz，Nevzat Ki-linc. Weapon selection using the AHP and TOPSI-S methods under fuzzy environment［J］.Expert Systms with Applications，2009，36:8143 -8151.

［11］HE Ke-qiang，，JIA Yu-yue，Wang Bin，et al . Comprehensive fuzzy evaluation model and evaluation of the karst collapse susceptibility in Zaozhuang Region，China［J］. Natural Hazards. 2013，68(2):613 -629.

［12］ZHANG Jing，WANG Xin-yi，CAOMo.New LCA approa-ch with fuzzy evaluation［J］.Journal of Bering Institute ofTechnology，2001，10(1):56 -62.