電偶極子激發(fā)的電場及其MATLAB軟件的模擬仿真

矯洪楠 侯 恕

(東北師范大學物理學院 吉林 長春 130024)

1 MATLAB簡介

1.1 MATLAB軟件

MATLAB是MathWorks公司推出的用于科學和工程計算的交互式軟件系統(tǒng).它以矩陣作為數(shù)據(jù)操作的基本單位,提供數(shù)值計算函數(shù),具有強大的數(shù)值計算與分析功能. MATLAB 與符號計算語言Maple結合,從而具有符號計算功能. MATLAB還具有繪圖功能,也可以對圖形進行修飾和控制,其數(shù)據(jù)處理能力和工具箱亦使得用它編程比傳統(tǒng)的編程問題容易、簡便[1].因此, MATLAB既是一種編程環(huán)境,又是一種程序設計語言,與高級程序語言C和Fortran相比更加數(shù)學化,使用起來也更方便,但是MATLAB是解釋性語言,程序執(zhí)行速度較慢,而且不能脫離MATLAB環(huán)境而獨立運行.

1.2 用MATLAB模擬電偶極子場分布的優(yōu)點

首先用MATLAB可以實現(xiàn)模擬電偶極子周圍場分布,以實現(xiàn)物理模型的可視化.其次，給定空間任意一點坐標，即可用給定的公式計算這一點的電位，對電位求梯度可得到空間任意一點的場強表達式.再次，可以用MATLAB實現(xiàn)電偶極子近區(qū)場分布的模擬以及遠區(qū)輻射場的模擬，這對于充分理解電偶極子的場分布具有重要的作用.

2 偶極子簡介

2.1 電偶極子

電偶極子是指一對等值異號的點電荷相距一微小距離所構成的電荷系統(tǒng)，它是一種常見的場源存在形式.它同點電荷、分子電流等一樣是電磁學中的一個重要物理模型.特別是在電介質(zhì)極化理論及天線理論中,電偶極子是一個基本模型[2].

2.2 電偶極子激發(fā)的遠區(qū)場

圖1表示中心位于坐標系原點上的一個電偶極子，它的軸線與z軸重合，兩個點電荷q和-q間的距離為L.此電偶極子在場點P處產(chǎn)生的電位等于兩個點電荷在該點的電位之和，即

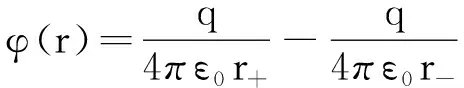
(1)

其中r+與r-分別是q和-q到P點的距離.

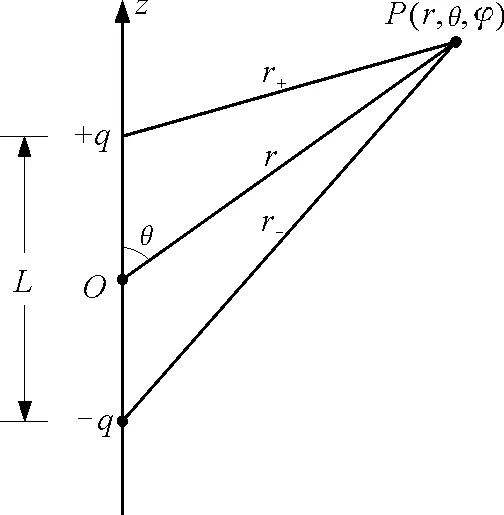
圖1 電偶極子

一般情況下，我們關心的是電偶極子產(chǎn)生的遠區(qū)場，即電偶極子到場點的距離r遠遠大于偶極子長度L的情形，此時可得到電偶極子的遠區(qū)表達式

(2)

可見電偶極子的遠區(qū)電位與qL成正比，與r的平方成反比，并且和場點位置矢量r與z軸的夾角θ有關.

為了便于描述電偶極子，引入一個矢量p，該矢量的模p=qL，方向由-q指向q，稱之為此電偶極子的電矩矢量，簡稱為偶極矩，記作

p=qL

(3)

此時式(2)又可以寫成

(4)

電偶極子的遠區(qū)電場強度可由式(4)(球坐標系)求梯度得到.因電位φr只是坐標r和θ的函數(shù)，于是有

E=-

(5)

從式(4)和式(5)可以看到，電偶極子的遠區(qū)電位和電場分別與r的平方和r的三次方成反比.因此，其電位和場強隨距離r的下降比單個點電荷更為迅速，這是由于兩個點電荷q和-q的作用在遠區(qū)相互抵消的緣故.

根據(jù)式(4)，電偶極子的等電位面方程可由式(2)為定值得到.

將電場線微分方程寫成球坐標形式，并注意此時電場只有r和θ兩個分量，有

(6)

把電場表達式(5)帶入式(6)，得

(7)

解式(7)得

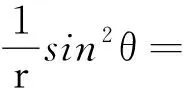
(8)

式(8)即是電偶極子遠區(qū)場的電場線方程.

圖2繪出了電偶極子在φ為常量的平面內(nèi)，式(8)取不同的常量所對應的等電位線和電場線.

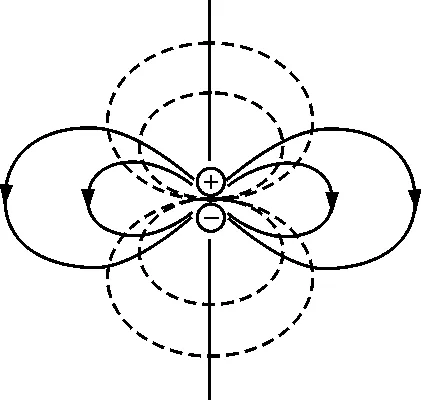
圖2 電偶極子的電場線與等位線

需要說明的是圖中準確的只是電場線的形狀，電場線的疏密并不嚴格與場強成正比，只是疏的地方場強小些，密的地方場強大些而已.

前面討論了電偶極子的中點位于坐標系原點且偶極矩方向為z方向的情況.對于中點不在原點和偶極矩非z方向的一般情況，通過與前面類似的推導，可以得到遠區(qū)的電位

(9)

其中，er是電偶極子中心指向場點P的相對單位位置矢量，偶極矩p=qL，L的方向依然規(guī)定為從-q到q.

經(jīng)推導還可得到遠區(qū)場的電場強度表達式

E=-

(10)

由式(10)可以看出,電偶極子的電場線均分布于子午面上,即由r,θ構成的平面上,并且任意一個子午面上的電場線分布都相同.

從以上幾種不同情況下電偶極子在空間激發(fā)的電場結果來看, 電場強度與p=qL成正比, 與源點到場點的距離r的三次方成反比,電偶極子在遠處的性質(zhì)是由其電偶極矩來表征的. 電偶極矩是電偶極子的重要特征. 研究電偶極子在空間激發(fā)的電場為分析電介質(zhì)的極化現(xiàn)象、電磁波的發(fā)射、吸收以及輻射等奠定了重要的理論基礎.

3 MATLAB軟件模擬電偶極子過程

3.1 建立模型

空間任意一點的電位為

在直角坐標系中可確定r+及r-與空間任意位置坐標的關系

(11)

因此，只要給定空間任意一點的位置坐標P(x，y，z)，就可以算出這一點的電位.

3.2 流程圖

程序流程圖如圖3所示，其主要步驟如下.

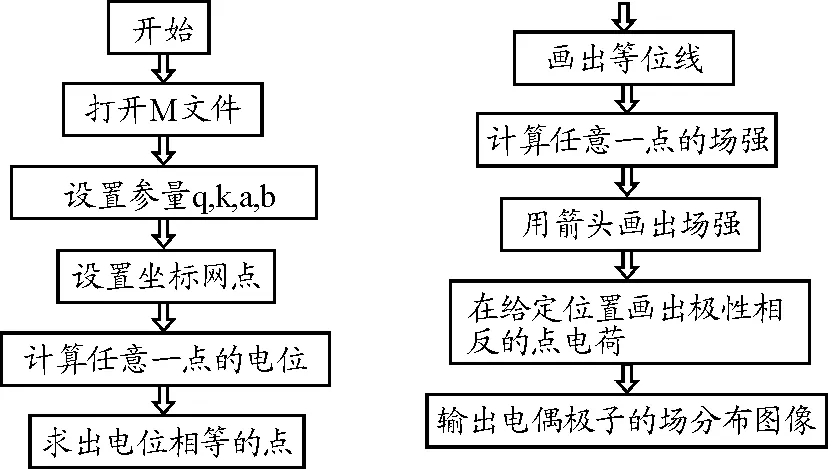
圖3

3.3 演示程序及圖形

用MATLAB模擬電偶極子場分布(二維情況)的程序(略).

用MATLAB模擬電偶極子場分布(三維情況)的程序如下：

clear;

b=1.5;

x=-10∶0.6∶10;

y=x;

[X,Y]=meshgrid(x,y);

U=(1./rp-1./rn);

clf;

surf(X,Y,U)

box on

axis tight

alpha(0.8)

shading interp

hold on

plot3([0;0],[1.5;-1.5],[0;0],′r′,′LineWidth′,1)

plot3(0,1.5,0,′ro′,0,1.5,0,′r+′)

plot3(0,-1.5,0,′ro′,0,-1.5,0,′r-′)

title(′電偶極子電勢三維分布′,′FontSize′,16)

xlabel(′X′,′FontSize′,16)

ylabel(′Y′,′FontSize′,16)

zlabel(′U′,′FontSize′,16)

u=0.5∶0.25∶3;

由以上程序所得到的圖形如圖4所示.

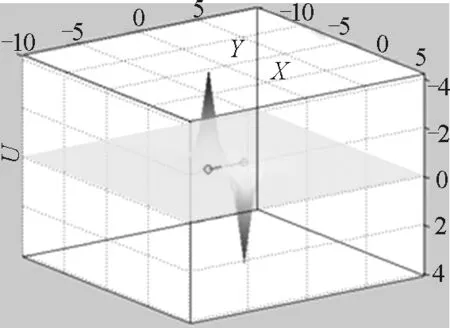
圖4 電偶極子電勢三維分布圖形

4 結果分析

本文得到的電偶極子的場分布圖形既形象又直觀，模擬的過程簡單易懂.在電磁場輻射研究中, 由于電磁場的不可觸和不可視性, 使理論過于抽象.電偶極子是研究電磁場輻射過程中最具代表性的物理模型, 如果我們充分地理解了電偶極子的輻射, 就可以更加深入了解電磁波輻射.本文的分析無論用于電磁場輻射的理論研究與說明, 還是用于相關物理現(xiàn)象的探索, 都是非常有意義的.在條件許可的情況下, 也可以用于教學課堂的演示,從而把復雜的物理現(xiàn)象直觀地展示出來.

5 需要的改進

通過計算機程序設計,我們對計算機編程技術有了一定的了解,并且對電偶極子這個最基本的物理模型也有了較為深入的認識.雖然用MATLAB得到了電偶極子的輻射模型,結果較為理想,但覺得這些程序還有一些需要改進.

(1)本文得到的電偶極子的場分布圖形是靜態(tài)的,另外,本次設計得到的圖形并不十分精確,而僅是給出了電場線的大體形狀,因此,如果我們能夠得到更加精確的圖像，將更加具有現(xiàn)實意義.

(2)模擬出來的圖形如果能夠采用動畫的形式播放,既可以用于教學,又可以給人以視覺上的享受,把抽象的問題具體化、圖形化.

參考文獻

1 高會生.MATLAB原理與工程應用(第1版).北京：電子工業(yè)出版社，2006.107～130

2 陳重.電磁場理論基礎 (第3版).北京：北京理工大學出版社,2003.63～70

3 陳軍, 田亞蘭, 于成，等．ScienceWord軟件輔助高中物理教學實踐的初級應用．物理教師，2009(2)：39～40