基于一致性準則的屬性約簡改進算法

陳媛，茍光磊，盧玲

(重慶理工大學計算機科學與工程學院，重慶 400054)

基于一致性準則的屬性約簡改進算法

陳媛，茍光磊，盧玲

(重慶理工大學計算機科學與工程學院，重慶 400054)

針對基于粗糙集的連續值屬性約簡存在速度較慢的問題，提出一種改進的一致性準則的屬性約簡算法。從相對核的角度出發，將一致性準則的概念和屬性的重要度的概念結合運用，優化了原算法的結構，加快了屬性約簡的速度。實驗結果表明該算法有效可行。

粗糙集;一致性準則;屬性約簡;相對核

粗糙集理論由波蘭數學家Pawlak.Z在20世紀80年代初提出，用于處理不精確、不完整與不相容數據的數學理論［1］，在數據的決策與分析、機器學習與模式識別等多個領域得到了廣泛的應用［2］。針對連續值屬性的約簡，已有多種擴展粗糙集模型被用于研究。屬性約簡是粗糙集理論的核心內容之一，其主要思想是在保持某種能力不變的前提下，刪除冗余或不重要的屬性，從而減少搜索空間，提高效率。在處理連續值屬性的約簡時，一是將連續值屬性離散化，用離散值屬性約簡算法處理連續值屬性約簡，但該方法只適合處理少量的連續值屬性的約簡;二是直接使用拓展粗糙集模型進行約簡。如胡清華教授等提出一種基于鄰域的屬性約簡算法［3］，但該算法需求解各對象的鄰域，計算代價過高，且鄰域參數的選取缺乏理論上的合理解釋［4］。南京師范大學的楊明教授提出了一種基于一致性準則的屬性約簡算法ARBCC(attribute reduction based on consistency criterion)，該算法無須計算各對象的鄰域，理論分析和實驗結果證明該算法是有效可行的。

文獻［4］提出一種基于一致性準則的屬性約簡算法，可針對離散值或連續值屬性進行有效的約簡。但當處理的數據集中含有眾多屬性時，數據的分類速度不是很理想。本文針對文獻［4］的算法，提出一種改進的一致性準則的屬性約簡算法。該算法以決策表的相對核為起點，在決策表中添加屬性時，引起決策表一致性量的變化，用變化的大小來反映該屬性的重要程度，即R=R∪{a}。該算法將一致性準則的概念和屬性重要度的概念結合運用，優化了算法的結構，加快了約簡的速度，并通過實例分析驗證了改進算法的有效性。

1 粗糙集理論的基本概念

設DT=(U，AV，f)為一個信息系統。其中:U是非空對象集合，稱為論域;A=C∪D是屬性集合，C和D分別為條件屬性集和決策屬性集。具有條件屬性集和決策屬性集的信息系統稱為決策表，設P?A是U上的一個等價關系，即

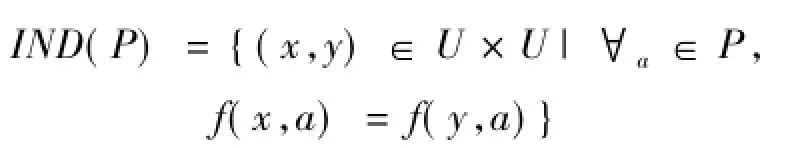
其中:x，y為U中的對象;V=∪Va，Va為a屬性的

a∈A值域集;信息函數f:U×A→V指定U中每個對象的屬性值［5－6］。

定義1設P?C，P為C的D約簡，當且僅當P是C的D獨立子集族，且posP(D)=posC(D)，則P是D的相對約簡。P中所有D的等價關系構成的集合稱為P的D核，即相對核。

定義2［7］設U為一個論域，P為定義在U上的一個等價關系族，P中所有必要關系組成的集合稱為族集P的核，記作Core(P)。

定理1core(P)=∩red(P)，其中red(P)表示屬性集P的所有約簡。

證明反證法。設A，B，C為屬性集P的所有約簡，若core(P)≠∩red(P)，必有A∩B∩C= φ，這與A∩B∩C≠φ矛盾，故假設不成立。

從定理可知，核概念的使用有2個方面:

1)可以作為所有約簡的計算基礎，由核的定義可知，核包含在所有的約簡之中。

2)核可以被解釋成屬性最重要部分的集合，在進行屬性約簡時是不能去掉的。

2 改進的一致性準則的屬性約簡算法

本文首先對一致性和不一致性的概念及其性質進行介紹。

定義3［8］設DT為一決策表，P?C，對2個對象x，y∈U，f(x，D)≠f(y，D)，若有dp(x，y)＞ε (其中ε≥0)，則稱x，y在p上是ε－一致的;否則，x，y在p上是ε－不一致的。其中dp(x，y)表示2個對象x和y之間的不相似度或距離，即

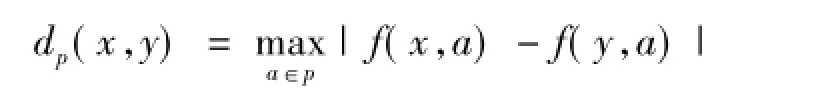
根據定義4，可以將任意兩個對象的一致性概念推廣到一組對象在某個屬性集上的一致性，即定義5。

為保證快速有效地得到屬性約簡，需了解在屬性集擴大的情況下，一致性對象的變化情況。

定理2給定ε(ε≥0)，對任意的A?B，B?C，①設dA(x，y)＞ε，則有dB(x，y)＞ε成立;②若x(x∈U)是關于A的ε－一致對象，則x(x∈U)是關于B的ε－一致對象。

證明

1)反證法:假設dB(x，y)≤ε，因A?B，則存在dA(x，y)≤ε，這與dA(x，y)≤ε矛盾，故假設不成立。

2)反證法:假設x(x∈U)是關于B的ε－不一致對象，對?y∈U，dB(x，y)≤ε，則存在f(x，D)= f(y，D);由于A?B，則x，y在屬性A上必然存在f(x，D)=F(y，D);又有dA(x，y)＞ε，則x是關于A的ε－不一致對象，這與x(x∈U)是關于A的ε－一致對象矛盾，故假設不成立。

由定理2可知:改進的一致性準則的屬性約簡算法具有單調性。

根據定理2，若給定的不相似度滿足單調性，則通過逐步擴展重要屬性即可得到一個有效的屬性約簡。本文提出了一種改進的屬性約簡算法，以決策表的相對核為起點，逐步添加增量最大的屬性，最后得出屬性約簡。

定義4給定ε(ε≥0)，A?C，定義差別矩陣MA={MA(x，y)}為

從定義4可以看出:對任意的兩個元素x，y∈U，dp(x，y)≤ε，說明對象x，y在p上不一致。在條件屬性P下，決策表對應的差別矩陣中含有矩陣分量值為1的元素越多，說明屬性越重要，否則說明該屬性越不重要。

本文提出的改進一致性準則約簡算法逐次選擇最重要的屬性添加到相對核中，直到滿足終止條件。IARBCC(improved attribute reduction based on consistency criterion)算法具體描述如下:

輸入1)決策表

2)一致性參數

輸出該決策表的一個屬性約簡R

主要步驟

1)求核core:

①初始化核core=?;

②對?a∈C，x，y∈C－a，有f(x，D)≠f(y，D)且dC－a(x，y)≤ε，則說明為核a;

2)對全部數據的全部屬性求其一致性量;

3)令R=core，計算R的一致性量;

4)對?a∈C－R，計算R+a的一致性量:

①初始化區別矩陣中數值為 1;

②計算MR+a，即計算所有對象關于當前屬性集的不一致性(0的個數);

③計算矩陣中1的個數;

④判斷該屬性是否為C－R中最后一個屬性，如果是，轉5，否則，轉 4;

5)找出一個數最多的屬性，即該屬性為最重要的屬性，有R=R+a;

6)計算R的一致性量，當R的一致性量等于全部數據全部屬性的一致性量時，算法終止，否則，轉4)。

3 實驗分析

3.1 適合約簡的屬性集

本文的實驗采用文獻［4］中的部分數據集，其描述如表1所示。

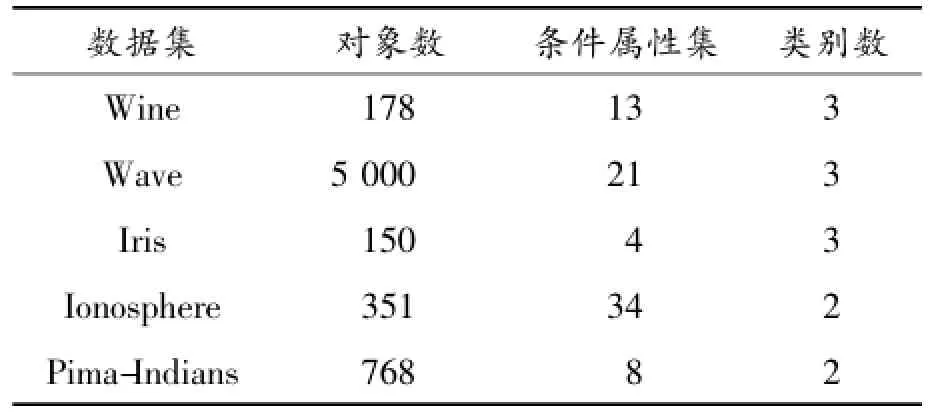
表1 數據集的描述

其中:Iris的屬性為離散值屬性，即ε=0。對Iris數據集進行屬性約簡，得到屬性約簡R={1，3，4}。由此可知:必須有3個條件屬性才能將Iris數據集區分開。因此，Iris數據集不具有屬性約簡的價值。所以，本章采用剩余4個數據集來進行實驗。

3.2 ε的取值

為了解一致性參數ε與屬性約簡結果之間的關系，本文對Wine和Wave數據集進行了處理和分析，所得結果如表2、3所示。

從表2可見:當ε取0.15或更小的值時，屬性可以約簡，但由于沒有產生相對核，所以ε在該范圍內取值對本算法而言是無效的;當ε在［0.175，0.181 8］內取值，屬性可以約簡，同時產生了相對核，ε在該范圍內取值對本算法是有效的;隨著ε取值的不斷增大，屬性無法約簡。同樣，從表3可以得出:當ε在(0.095，0.097］內取值時，對本算法是有效的。由此說明本文提出的算法在某些情況下是有效的。

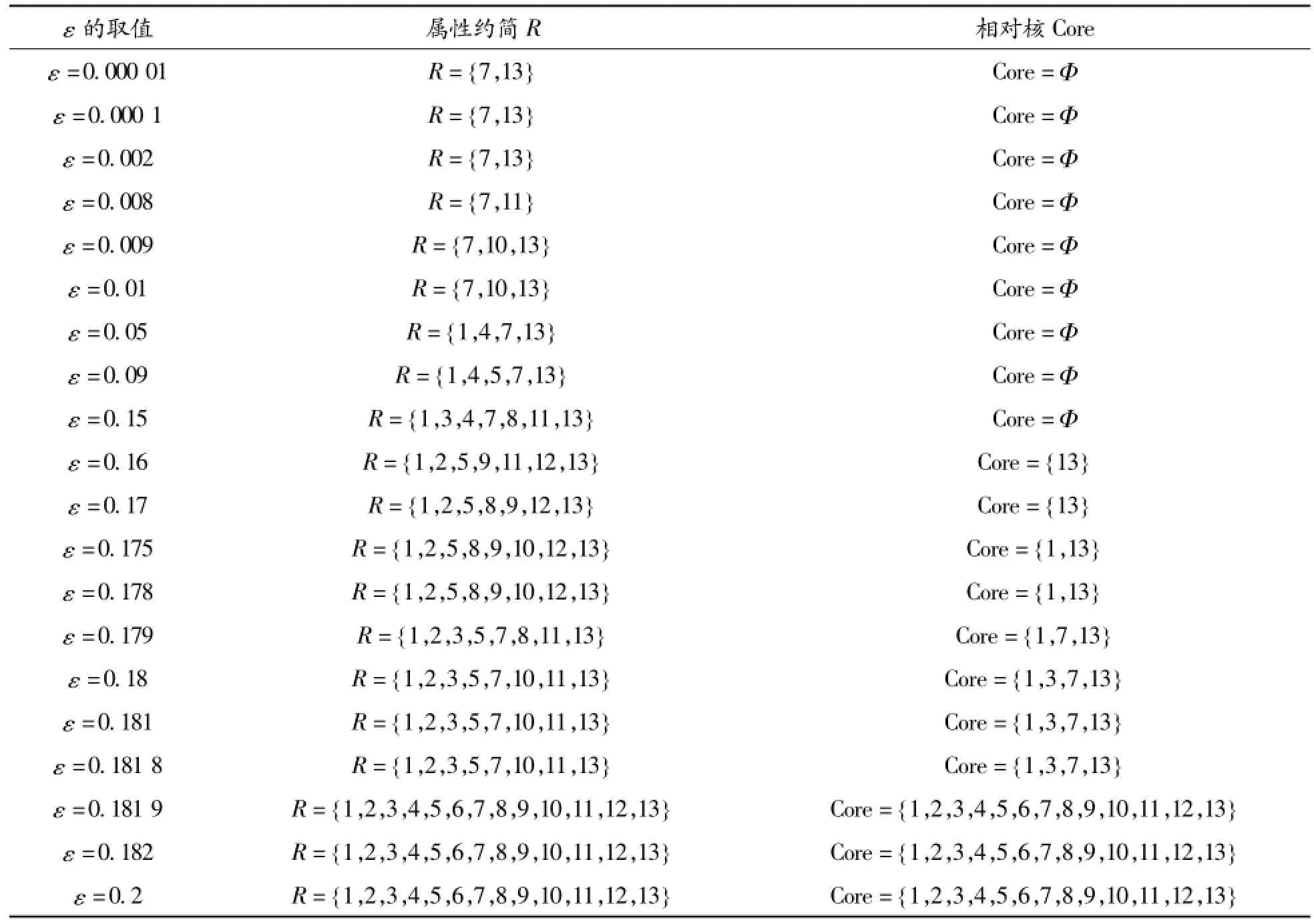
表2 Wine數據集中ε的取值與屬性約簡和相對核之間的關系

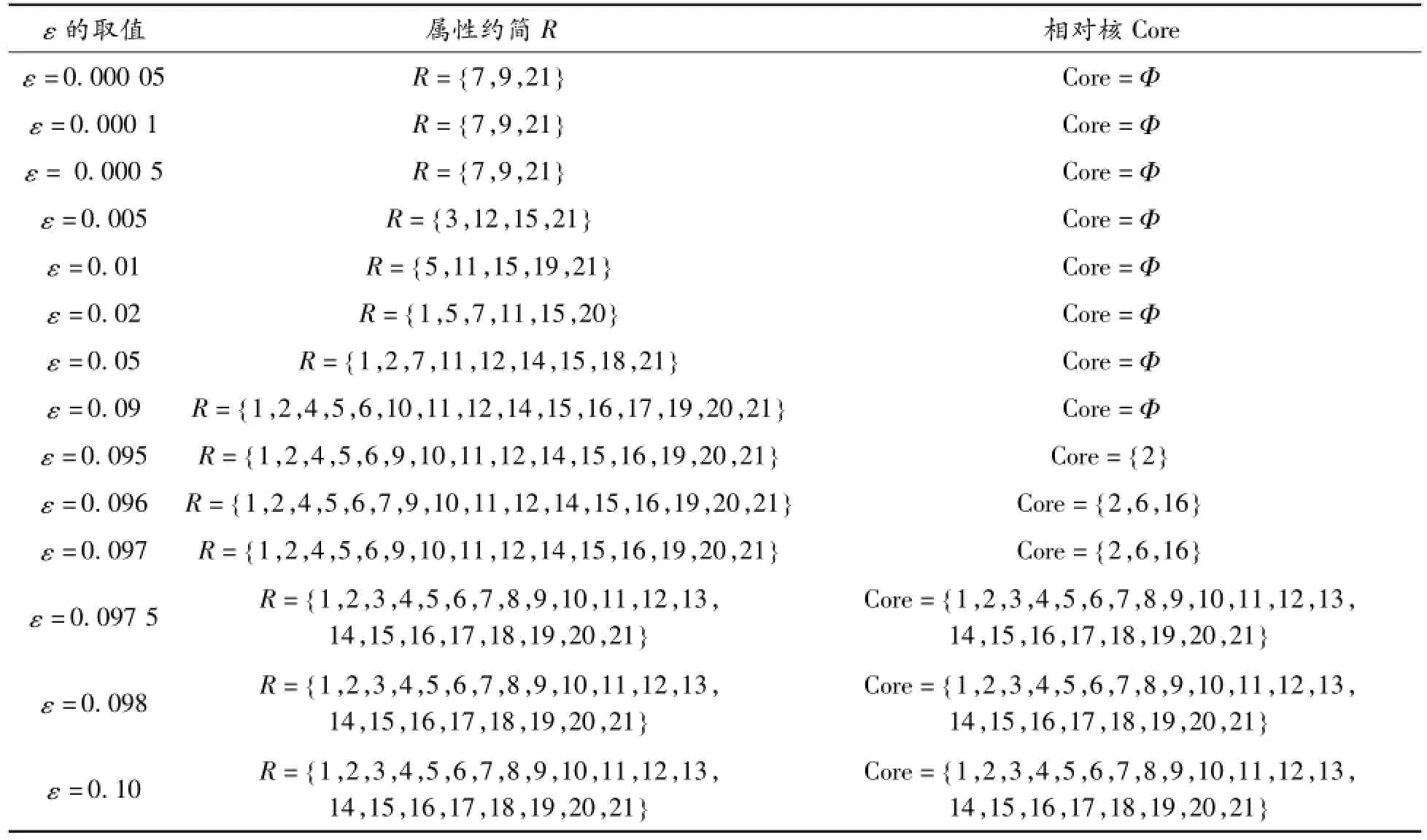
表3 Wave數據集中ε的取值與屬性約簡和相對核之間的關系

3.3 實驗結果

選取適合的數據集以及相對應的一致性參數ε，對ARBCC算法和IARBCC算法進行決策表的運行效率和分類精度在內的算法的有效性分析。

首先，比較ARBCC算法和IARBCC算法在一致性參數ε不變、數據集變化情況下的執行效率。本文從Wave中隨機抽取了500到3 000的一系列數據，對一致性參數ε=0.095和ε=0.097，分別比較ARBCC算法和IARBCC算法的執行效率。所得結果如圖1所示。

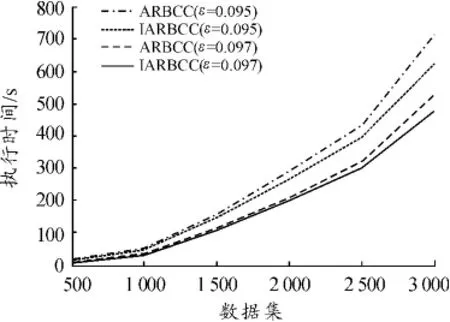
圖1 算法ARBCC和IARBCC的運行時間

圖1的實驗結果表明:IARBCC算法比ARBCC算法擁有更快的運行速度。

針對Wine數據集，在一致性參數ε變化的情況下，ARBCC算法和IARBCC算法的分類精度和執行時間情況如圖2、3所示。

觀察圖2、3的實驗結果可知:無論是對小樣本數據集還是大樣本數據集，IARBCC算法都比ARBCC算法擁有更高的屬性約簡的效率。

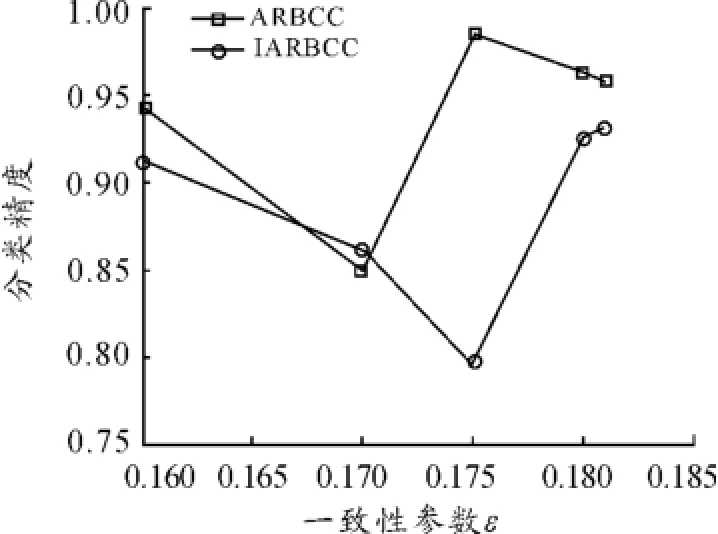
圖2 算法ARBCC和IARBCC的分類精度隨一致性參數ε的變化

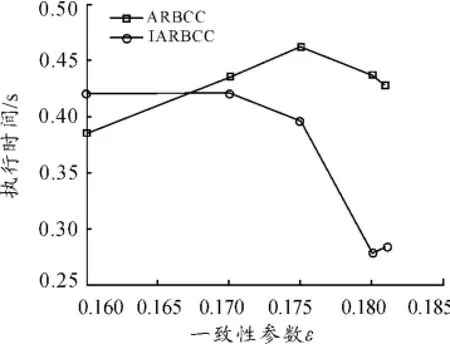
圖3 算法ARBCC和IARBCC的執行時間隨一致性參數ε的變化

最后，針對Ionosphere和Pima數據集，分析ARBCC算法和IARBCC算法的執行時間。實驗結果如表4所示。

表4 運行速度的對比

從表4的實驗結果可見:與ARBCC算法相比，IARBCC算法加快了運行的速度。

綜合分析上述的實驗結果，在分類精度保持不變或較高的情況下，與ARBCC算法相比，IARBCC算法是有效可行的。它有效地改進了屬性約簡的效率，提高了運行的速度。在對屬性眾多的數據集進行約簡時，這種改進是十分必要的。

4 結束語

目前，粗糙集被廣泛應用于各個領域，屬性約簡成為信息科學研究的熱點之一。面對復雜的數據，如何高效地進行連續值屬性約簡已成為當前粗糙集研究的熱點。本文提出了一種改進的一致性準則的屬性約簡算法，該算法以ARBCC算法為BaseLise。實驗分析結果表明:本文方法取得了比BaseLise算法更快的運行速度，證明了該方法的有效性。

［1］Pawlak Z.Rough Sets［J］.International Journal of Information and Computer Science，1982，11(5):341－365.

［2］Pawlak Z.Rough Sets and Intelligent Data Analysis［J］.Information Science，2002，147(1－4):1－12.

［3］胡清華，于達仁，謝宗霞.基于鄰域粒化和粗糙逼近的數值屬性約簡［J］.軟件學報，2008，19(3):640－649.

［4］楊明.一種基于一致性準則的屬性約簡算法［J］.計算機學報，2010，33(2):231－238.

［5］張文修，仇國芳.吳偉志.粗糙集屬性約簡的一般理論［J］.信息科學，2005，35(12):1304－1313.

［6］宋佳娟，曲朝陽，李翔坤.基于信息熵的粗糙集屬性約簡算法研究［J］.軟件時空，2010，26(6－3):212－214.

［7］吳尚智，茍平章.粗糙集和信息熵的屬性約簡算法及其應用［J］.計算機工程，2011，37(7):56－59.

［8］陳堃，李心科.基于一致性度量的屬性約簡的研究［J］.計算機技術與發展，2008，18(10):64－67.

(責任編輯 楊黎麗)

Improved Algorithm for Attribute Reduction based on Consistency Criterion

CHEN Yuan，GOU Guang－lei，LU Ling
(School of Computer Science and Engineering，
Chongqing University of Technology，Chongqing 400054，China)

To solve the low efficiency of reduction of continuous－valued attributes based on rough sets，an improved attribute reduction algorithm based on consistency criterion is proposed.From the view of relative core，the concept of consistency criterion and important degree of attributes is used to optimize the structure of the original algorithm and improve the efficiency.The experiment results show that this algorithm is feasible and effective.

rough set;consistency criterion;attribute reduction;relative core

TP18

A

1674－8425(2014)05－0079－05

10.3969/j.issn.1674－8425(z).2014.05.016

2014－01－20

陳媛(1966—)，女，重慶人，教授，主要從事智能信息處理研究。

陳媛，茍光磊，盧玲.基于一致性準則的屬性約簡改進算法［J］.重慶理工大學學報:自然科學版，2014(5): 79－83.

format:CHEN Yuan，GOU Guang－lei，LU Ling.Improved Algorithm for Attribute Reduction based on Consistency Criterion［J］.Journal of Chongqing University of Technology:Natural Science，2014(5):79－83.