模糊PID控制在磁懸浮系統中的應用

宋榮榮，馬衛華

(1.西南民族大學計算機科學與技術學院，成都 610041; 2.西南交通大學牽引動力國家重點實驗室，成都 610031)

模糊PID控制在磁懸浮系統中的應用

宋榮榮1，馬衛華2

(1.西南民族大學計算機科學與技術學院，成都 610041; 2.西南交通大學牽引動力國家重點實驗室，成都 610031)

基于模糊控制的思想，建立以懸浮系統為對象的數學模型，根據懸浮系統自身特點并結合實際經驗，找出輸入變量誤差E和誤差變化率EC與PID的3個參數之間的模糊關系，制定模糊控制規則，設計了一種模糊自整定PID控制器。該控制策略的優點是能在懸浮系統工作時，對PID參數進行在線調節，以適應軌道不平順的變化，使控制器跟蹤精度高，響應速度快，魯棒性好。利用Matlab中Fuzzy和M函數的有機結合，通過仿真驗證了模糊自整定PID控制系統的可行性。結果表明:與傳統的PID控制器相比，該方法能夠對軌道的正弦波擾動和方波擾動實現更有效的跟蹤，對外加干擾具有更強的抑制能力。為解決軌道不平順問題提供了一種思路。

軌道不平順;磁懸浮系統;模糊PID控制;Matlab仿真

在磁懸浮列車行駛過程中，軌道不平順是影響懸浮性能的一個重要方面。有效克服軌道干擾是提高懸浮控制系統性能的一個重要因素［1］。從列車運行的安全性和乘客乘坐的舒適性兩方面進行考慮，懸浮系統需能跟蹤軌道表面的變化，如彎道、坡道等;對由軌道表面的不平整帶來的低頻和高頻振動不敏感;同時還應該能有效克服由于車輛負載變化帶來的擾動。目前的控制算法大多是以懸浮間隙作為位置信號，并結合電磁鐵的加速度和線圈的電流等信號進行傳統的PID控制［2－3］。實踐證明:這種控制方法在克服軌道不平順帶來的影響方面效果并不理想。目前，很多國內外專家學者采用模糊控制的方法提高磁懸浮系統抗干擾的能力［4－10］。

模糊控制是近年來發展起來的一種新型控制方法［4］。其優點是無需受控對象的精確數學模型，它根據人工控制規則組織控制決策表，然后由該表決定控制量的大小。將模糊控制和PID控制器兩者結合，揚長避短，得到的這種Fuzzy－PID復合型控制器既具有模糊控制靈活性和適應性強的優點，又具有PID控制精度高的特點，對單磁鐵懸浮系統具有良好的控制效果，是近年來十分熱門的研究課題［5－10］。

本文首先建立單電磁鐵懸浮系統的數學模型，然后設計了一個模糊－PID復合型控制器。其主要思想是以誤差和誤差變化率作為輸入，利用模糊控制規則，在不同時刻對PID參數進行自調整。基于Matlab軟件的仿真結果表明:與傳統的PID控制器相比，該控制器對軌道干擾和負載擾動具有更好的抑制效果。

1 懸浮系統模型

單電磁鐵懸浮系統結構如圖1所示。假設電磁鐵不僅在垂直方向運動，還沿軌道以速度V運行。圖1中:絕對氣隙z(t)為磁極表面與絕對參考平面的距離;h(t)為軌道面與絕對參考平面的距離;相對氣隙c(t)為磁極表面與軌道面的氣隙;加速度計所測得的輸出為加速度¨z(t);氣隙傳感器測得的輸出為相對氣隙c(t);i(t)為電流互感器測得的控制線圈電流;u(t)為繞組回路的電壓。

圖1 單電磁鐵懸浮系統結構

設N為電磁鐵線圈的匝數，A為磁極面積，R為線圈的電阻，μ0為空氣磁導率，mg為電磁鐵重力，F(i，c)為懸浮電磁力，fd(t)為外界干擾力。

在分析單電磁鐵懸浮系統的動力學模型時，假設［11］:①忽略漏磁的影響;②忽略磁鐵芯和導軌中的磁阻，磁勢均勻降落在氣隙c(t)上;③電磁鐵僅有垂直方向上的移動，其他方向受限無運動。

根據電磁學和動力學理論，得到基于絕對參考平面的單電磁鐵動態模型方程:

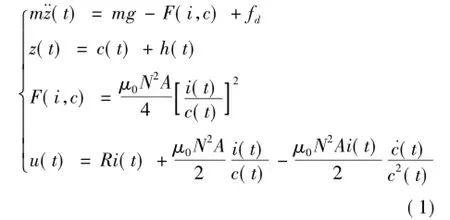
其中，平衡點的邊界條件為:

2 模糊PID控制器的設計

模糊PID控制器的關鍵技術是找出誤差E和誤差變化率EC與PID的3個參數之間的模糊關系。根據確定的模糊控制規則對PID的3個參數進行在線調整，滿足不同的E和EC對3個參數的要求，控制結構如圖2所示。

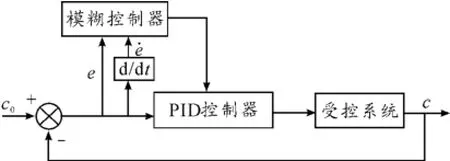
圖2 模糊PID控制結構

2.1 傳統PID控制器的參數設定

對系統(2)增加一個狀態變量∫Δc(t)dt，以電流為控制變量，得到開環系統的狀態方程:

比較閉環特征方程(4)和期望的閉環傳遞函數(5)，可求得參數Kp=19 638.65，KI=603 880.52，KD=215.68。

2.2 各變量隸屬函數的確定

以E和EC為輸入語言變量，以Δkp，Δki和Δkd為輸出語言變量。定義E和EC的模糊集均為{NB，NM，NS，ZO，PS，PM，PB}，控制量Δkp、Δki和Δkd的模糊集均為{NB，NM，NS，ZO，PS，PM，PB}。各變量的隸屬函數曲線分別如圖3～7所示。

圖3 變量E的隸屬函數

圖4 變量EC的隸屬函數

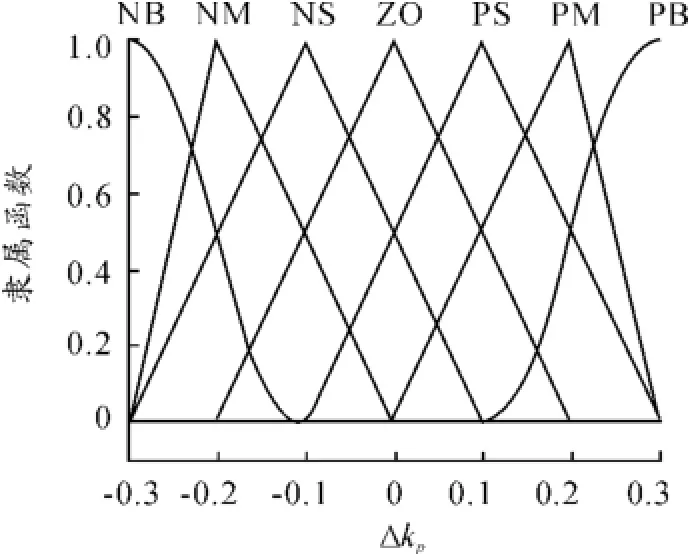
圖5 變量Δkp的隸屬函數

圖6 變量Δki的隸屬函數

圖7 變量Δkd的隸屬函數

2.3 模糊控制規則

模糊控制規則是模糊控制器設計的核心內容。根據單電磁鐵懸浮系統的特點與專家經驗，通過分析大量成功的控制策略經驗，制定模糊控制規則。制定的原則主要有:

1)仿真開始時，減少積分作用以防止飽和;仿真快結束時，增大積分作用以減少系統等穩態誤差。

2)誤差偏大時，增大比例作用以增加響應速度;誤差偏小時，增大積分作用以保證系統穩定。

3)誤差變化率偏大時，減少微分作用;誤差變化率偏小時，增大微分作用。

采用模糊規則“IF A AND B THEN C”形式制定。由于2個輸入變量各有7個語言值，因此分別建立Δkp，Δki和Δkd的49條模糊規則，見表1～3。

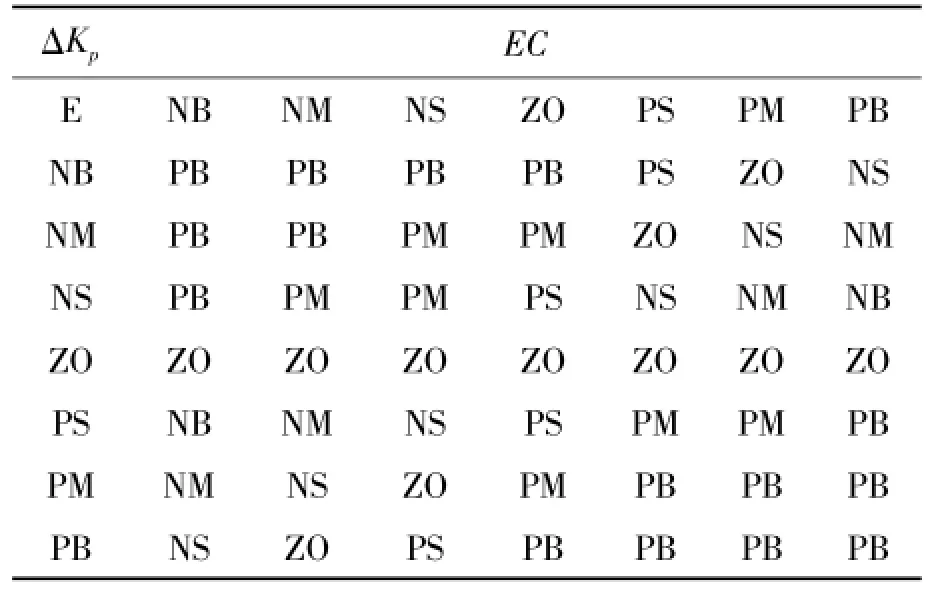
表1 Δkp的模糊規則

表2 Δki的模糊規則表

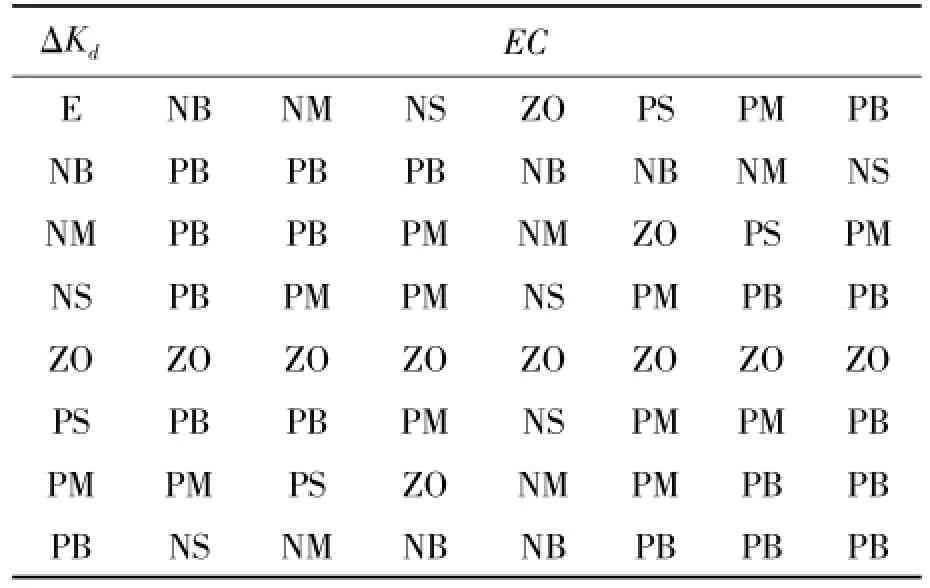
表3 Δkd的模糊規則表

根據上述模糊規則表，可以對kp，ki，kd進行動態整定。通過狀態方程(3)和期望的閉環傳遞函數(5)，求得k'p，k'i，k'd的預整定值分別為: k'p=19 638.65，k'I=603 880.52，k'D=215.68。選擇適當的模糊化和去模糊化方法，得到模糊PID參數分別為:kp=k'p+Δkp，ki=k'i+Δki，kd= k'd+Δkd。

3 Matlab仿真分析

采用計算機仿真軟件Matlab中的Fuzzy工具箱和M函數進行仿真［15］，驗證模糊自整定PID控制器的性能。設定采樣時間為1 ms，取1 000個采樣點。單電磁鐵懸浮控制系統的參數如表4所示:

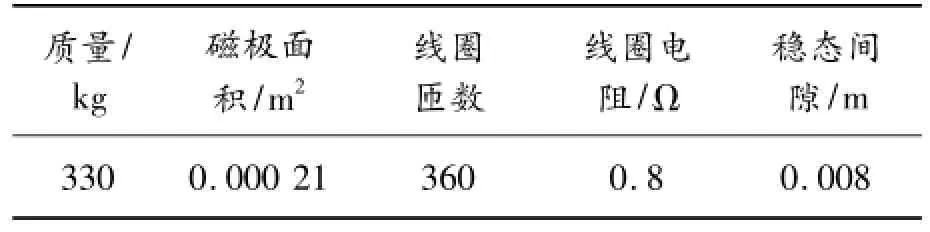
表4 單電磁鐵懸浮系統的參數

針對軌道干擾和負載干擾問題，對比傳統PID控制和模糊PID控制的跟蹤效果。

3.1 軌道正弦波擾動的跟蹤性能

設軌道不平順對應的正弦波信號的幅值為1 mm，振動頻率為2 Hz。仿真對比結果如圖8所示。

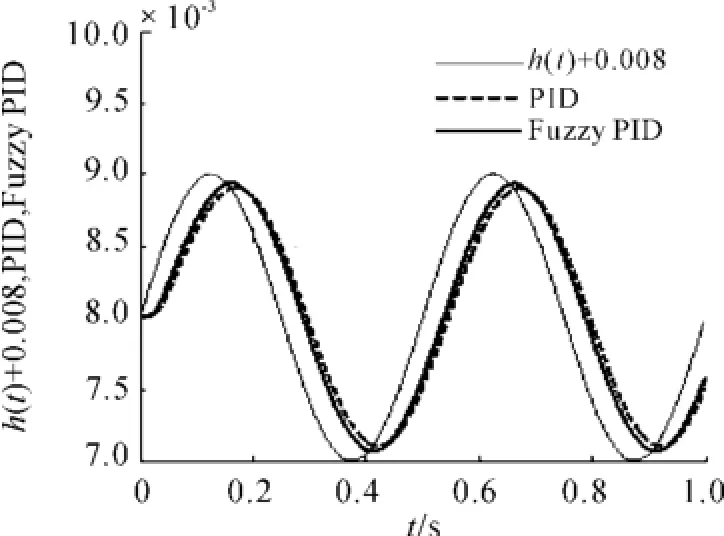
圖8 對軌道正弦波擾動的跟蹤性能比較

3.2 軌道方波擾動的跟蹤性能

設軌道不平順所對應的方波信號的幅值為0.001 mm，振動頻率為2 Hz。仿真對比結果如圖9所示。

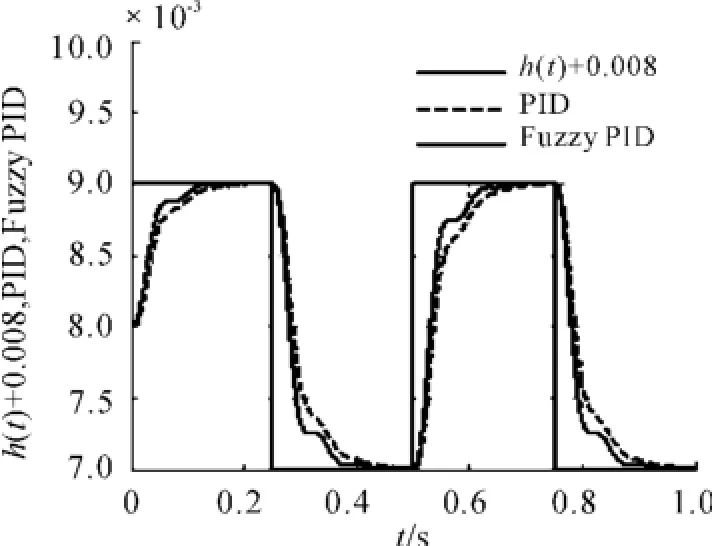
圖9 對軌道方波擾動的跟蹤性能比較

3.3 帶有干擾信號軌道階躍擾動的跟蹤性能

設軌道所對應的階躍信號為h(t)=0。在第300個采樣點處，加干擾ξ(300)=0.005，仿真對比結果如圖10所示。

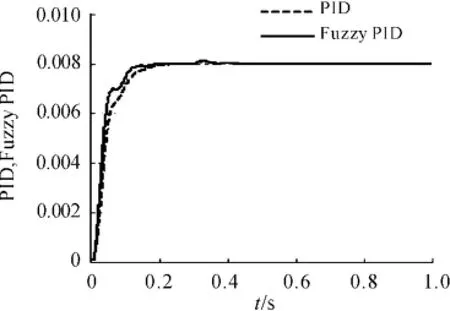
圖10 抗負載擾動的性能

4 結束語

本文首先建立3階懸浮系統，增加干擾項，然后以電流為控制量，基于模糊免疫PID控制器設計控制方案，利用PSO尋優算法求解控制參數，最后，基于Matlab中的M函數形式進行軌道不平順的跟蹤研究。研究結果表明:

1)由于軌道不平順對懸浮系統的影響，因此懸浮系統的控制性能對PID控制參數有很強的依賴性。要克服軌道干擾，就必須在線調整控制參數以獲得最佳的系統控制特性。模糊自整定PID控制可以根據模糊控制規則實現在線調整PID參數的功能。

2)對于軌道的正弦波擾動及方波擾動，與傳統的PID相比，模糊自整定PID控制均表現出較好的跟蹤性能;對于負載擾動，該系統有較好的抑制性能。上述結果表明:與傳統的PID控制相比，模糊自整定PID控制能夠更好地解決軌道不平順問題。

一個理論必須在實踐中得到成功的應用才能推動其不斷完善和向前發展，模糊控制理論亦如此。今后的研究將考慮如何將其和智能控制的方法相結合，以更好地應用于磁懸浮控制。

［1］Zhiqing Long，Guohua Shi，Lianchun Wang.Suspension influence analysis of track irregularity of maglev train［C］//Control and Decision Conference.［S.L.］:［s.n.］，2010:942－947.

［2］Hengkun Liu，Xiao Zhang，Wensen Chang.PID control to Maglev train system［C］//Industrial and Information Systems，［S.l.］:［s.n.］，2009:341－343.

［3］Moazen M，Sharifian M B B，Afshari H.PID control of Maglev guiding system for linear elevator［C］//Power E－lectronics，［S.l.］:［s.n.］，2012:1－6.

［4］汪培莊，李洪興.模糊系統理論與模糊計算機［M］.北京:科學出版社，1996.

［5］Shing－Jen Wu，Cheng－Tao Wu，Yen－Chen Chang.Neural－Fuzzy gap control for a Current/Voltage－controlled 1/4－vehicle maglev system［J］.Intelligent Transportation Systems，2008(9):122－136.

［6］Ahmad A K，Saad Z，Osman M K，et al.Control of magnetic levitation system using fuzzy logic control［C］// Computational Intelligence，Modelling and Simulation (CIMSIM)，2010 Second International Conference on Digital Object Identifier.［S.l.］:［s.n.］，2010:51－56.

［7］Yang Xia，Gao Yan，Du Jiguang.P－Fuzzy－PID control in a machine tool magnetic suspension system［C］//Electrical Machines and Systems，2008 ICEMS.USA:［s.n.］，2008:2201－2204.

［8］Jie Ma，Wenjun Fan，Fenghua He.Parameters self－adjusting fuzzy PID control in magnetic levitation system［C］//Systems and Control in Aerospace and Astronautics，2008 ISSCAA.USA:［s.n.］，2008:1－5.

［9］Trisanto A，Yasser M，Jianming Lu，et al.Implementation of a Fuzzy PID controller using neural network on the magnetic levitation system［C］//Intelligent Signal Processing and Communications.USA:［s.n.］，2006:669－672.

［10］Qing Hu，Hao Liu，Lisheng Ou.Fuzzy PID nonlinear control of maglev guiding system for linear elevator based in feedback linearization［C］//Fuzzy Systems and Knowledge Discovery(FSKD)，2010 Seventh International Conference.USA:［s.n.］，2010:1277－1280.

［11］宋榮榮.單電磁鐵懸浮系統的指數趨近律滑模控制［J］.重慶理工大學學報:自然科學版，2012，26(1): 11－16.

［12］李惠光，張廣路，周巧玲，等.垂直軸磁懸浮風電懸浮系統的模糊滑模控制［J］.武漢理工大學學報，2010，32(10):136－140.

［13］鄭大鐘.線性系統理論［M］.北京:清華大學出版社，2002.

［14］陶永華.新型PID控制及其應用［M］.北京:機械工業出版社，1998.

［15］張智星.Matlab程序設計與應用［M］.北京:清華大學出版社，2002.

(責任編輯 劉舸)

Application of Fuzzy PID Controller in the Magnetic Levitation System

SONG Rong－rong1，MA Wei－hua2
(1.College of Computer Science and Technology，Southwest University for Nationality，Chengdu 610041，China;2.Traction power state key laboratory Southwest Jiaotong University，Chengdu 610031，China)

Based on the theory of fuzzy control，the article established the mathematical model of the electromagnetic levitation system，found out the fuzzy relation between the three parameters of PID and the two input variables of error and error change rate and instituted the more appropriate fuzzy control rules according to the characteristics of single electromagnet levitation system combined with the expert experience.Then we designs a fuzzy self－tuning PID controller.The advantages of the control strategy is that it is able to adjust PID parameters online in the suspension system work adapting to the change of the track irregularity，which makes the controller to be high tracking accuracy，fast response，andgood robustness.Using the organic combination of Fuzzy and Simulink in Matlab，the fuzzy self－tuning PID control system is feasible through the simulation，the results shows that the fuzzy self－tuning PID control can be more effective to track rail low frequency changes，has stronger suppression ability for the high frequency vibration caused by the track irregularity compared with the traditional PID controller.The article provides a very good method for solving problem of track irregularity.

track irregularity;magnetic levitation system;fuzzy PID control;Matlab simulation

TP13

A

1674－8425(2014)05－0001－06

10.3969/j.issn.1674－8425(z).2014.05.001

2013－12－18

國家自然科學基金資助項目(51005190)，四川省科技支撐計劃項目(2012GZ0103)，西南民族大學中央高校專項資金項目(12NYZQN19)

宋榮榮(1979—)，女，博士研究生，副教授，主要從事泛函分析方面的研究。

宋榮榮，馬衛華.模糊PID控制在磁懸浮系統中的應用［J］.重慶理工大學學報:自然科學版，2014(5):1－6.

format:SONG Rong－rong，MA Wei－hua.Application of Fuzzy PID Controller in the Magnetic Levitation System［J］.Journal of Chongqing University of Technology:Natural Science，2014(5):1－6.