橢球體的視電阻率特征

張 超，湯井田，強建科

(中南大學(xué) 地球科學(xué)與信息物理學(xué)院， 長沙 410083)

0 前言

橢球體是最具代表性的典型三維地電體，它三個軸的長短變化后可以和多種形狀的地電體相似，球體、柱體、橢球柱體及板狀體都是橢球體的特例。因此實現(xiàn)了在常用場源激勵下橢球體電阻率的求解，就可以模擬絕大多數(shù)三維地電體的電阻率曲線。

J．H．Webb[1]提出了通過鏡像法推導(dǎo)均勻半空間點電流場中橢球體的精確解的思路[1];傅良魁等[2-3]研究了橢球類礦體(球體、圓柱體、橢球柱體)和橢球體的電阻率和形狀對礦頂上方視電阻率異常值大小的作用規(guī)律;宋子齊[4]對橢球類礦體的電場和磁場進行了一般性討論;雷林源[5]通過求解直角坐標(biāo)系中的拉氏方程，導(dǎo)出了橢球位函數(shù)的一般形式，并通過邊界條件和泊松公式，應(yīng)用橢球位場的一般形式給出了均質(zhì)橢球地質(zhì)體和均勻磁化橢球地質(zhì)體的重力位場和磁位場表達式;張秋光[6]詳細推導(dǎo)了橢球坐標(biāo)系下拉普拉斯方程的通解和均勻外磁場中的橢球體;羅延鐘等[7]給出了直流電法中和頻率域電法中傾斜旋轉(zhuǎn)橢球體的視電阻率公式;強建科等[8]計算了橢球體復(fù)電阻率相應(yīng)的幅頻率并討論了旋轉(zhuǎn)橢球體的充電率、中心埋深和長軸傾角對幅頻率異常和曲線形態(tài)的影響;徐淳寧等人[9]利用模擬電荷法對橢球體的電阻率曲線進行了數(shù)值計算;段長生[10]對不同場源的橢球異常進行了正演擬合反演并確定異常體的各模型參數(shù)。

1 均勻場中橢球體及板狀體的視電阻率公式

1.1 橢球坐標(biāo)系及其通解

對給定空間任意點P的直角坐標(biāo)(x，y，z)，解以下關(guān)于t的三次方程

(1)

可以求得三個不同的實根λ、μ、ν，且λ>-c2>μ>-b2>ν>-a2，這三個根(λ、μ、ν)稱為P點的橢球坐標(biāo)。

圖1 橢球坐標(biāo)系示意圖Fig．1 Schematic diagram of ellipsoid coordinate system

橢球坐標(biāo)系中拉普拉斯方程為：

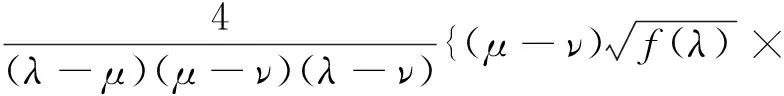
(2)

將公式(2)分離變量

φ=Λ(λ)Μ(μ)Ν(ν)

(3)

整理后可得到三個形式完全相同的拉梅函數(shù)，統(tǒng)一寫為

(4)

我們可以用公式(5)表示橢球內(nèi)部的拉普拉斯方程的解(有界)。

(5)

用式(6)表示橢球外部拉普拉斯方程的解。

(6)

1.2 均勻電場中橢球體的視電阻率

假設(shè)在電阻率為ρ1的均勻各向同性無限導(dǎo)電巖石中，有一個電阻率為ρ2，三個半軸分別為a、b、c的橢球體。取直角坐標(biāo)系，原點位于橢球體中心，坐標(biāo)軸X、Y、Z分別與a、b、c重合。均勻電流場的電流密度為j0，方向與X軸相同(見圖2)。

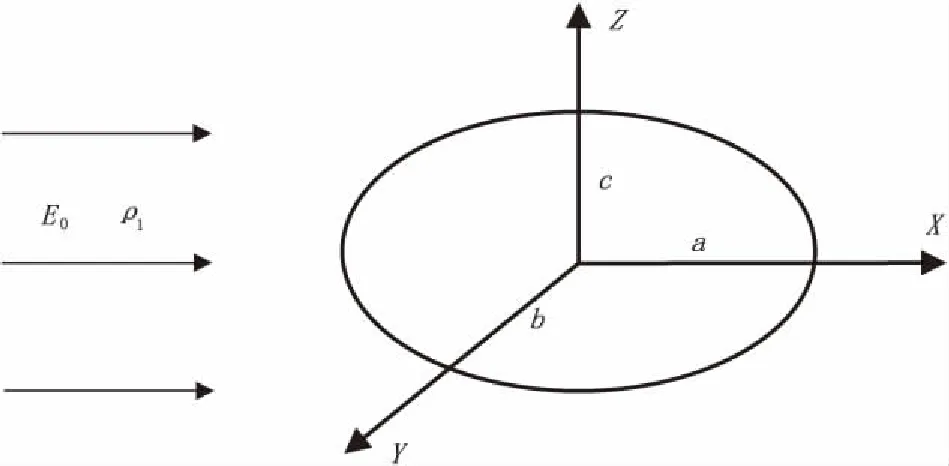
圖2 均勻電流場中的橢球體Fig．2 Ellipsoid in uniform electric field

橢球體內(nèi)、外的總場電位表達式：

(7)

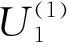
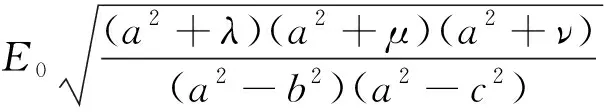
(8)

根據(jù)邊界條件， 橢球體與圍巖分界面上電位連續(xù)：

以及橢球體與圍巖分界面上電流密度法向分量連續(xù)：

(9)

式(9)可變形為式(10)。

(10)

經(jīng)過一系列計算與變量代換后，可得到橢球體內(nèi)、外的總場電位為式(11)。

(11)

其中

L=2πabc·

(12)

L0=2πabcIx=2πabc·

(13)

(14)

均勻半空間情況下，采用將異常電位加倍的近似方法得到橢球體外部電位：

(15)

將E0=j0ρ1代入公式(9)得式(16)。

(16)

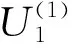
(17)

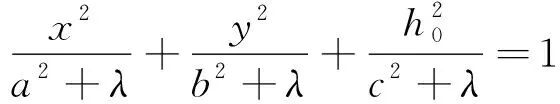
(18)

h0為橢球體中心埋深。

因此地面上沿x方向的視電阻率表達式為式(19)。

ρs=(1+2F1g′)ρ1

(19)

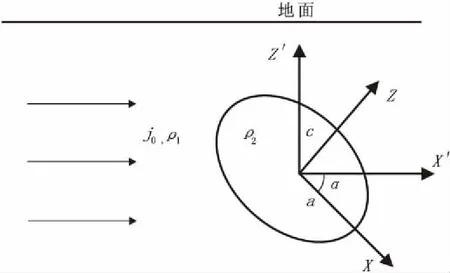
圖3 均勻電流場中的傾斜橢球體Fig．3 Inclined ellipsoid in uniform electric field

1.3 均勻電場中傾斜橢球體的視電阻率

如圖3所示為均勻電場中的傾斜橢球體。在求解傾斜橢球體時，用到了兩套坐標(biāo)系：XYZ坐標(biāo)系-分別與橢球體的三個軸重疊；X′Y′Z′坐標(biāo)系-X′的正方向與電流密度方向相同(即水平方向)，Z′的正方向垂直于水平地面，Y軸和Y′軸的正方向均垂直紙面向里。它們的轉(zhuǎn)換關(guān)系為：

(20)

其中α為X軸逆時針旋轉(zhuǎn)與X′軸的夾角，α∈[0,π)。

在推導(dǎo)出均勻電場中水平橢球體和直立橢球體的視電阻率公式之后，通過觀察傾斜旋轉(zhuǎn)橢球體公式的特點，導(dǎo)出傾斜橢球體的視電阻率的表達式：

ρs={1-2[Vx·R·cos2α+(Vx+Vz)·S·

sinα·cosα+Vz·T·sin2α]}ρ1

(21)

(22)

其中

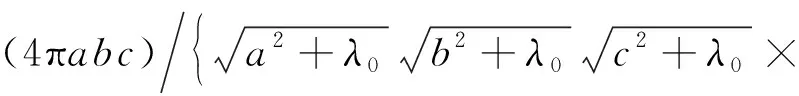
(23)

(24)

(25)

電性因子：

(26)

1.4 均勻場中的傾斜板狀體

板狀體由橢圓柱體近似得到。當(dāng)b→∞，a遠大于c(a?c)時，可得到柱軸平行地面的橢球柱體的視電阻率表達式，公式仍有前式的形式，不過當(dāng)中各因子都有所簡化。

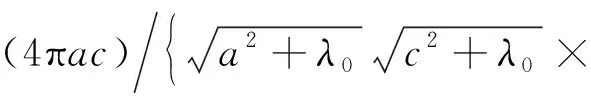
(27)

(28)

(29)

2 不同模型的視電阻率特征

2.1 旋轉(zhuǎn)橢球體的視電阻率曲線特征

圖4為低阻旋轉(zhuǎn)橢球體的視電阻率曲線，模型參數(shù)為長軸a=10,兩短軸b=c=2，中心埋深h=13。旋轉(zhuǎn)橢球體分別沿順時針旋轉(zhuǎn)0°、30°、60°和90°。當(dāng)?shù)妥栊D(zhuǎn)橢球體水平或直立時，視電阻率曲線關(guān)于中心對稱，且直立橢球體的極小值相比水平橢球體更小；當(dāng)橢球體傾斜時，異常體頂部附近的視電阻率異常為零，在傾向一側(cè)有極小值，在反傾向一側(cè)有極大值，且傾角α越大，極大值越大；隨著傾角α的增大，曲線逐漸變陡。

圖4 低阻旋轉(zhuǎn)橢球體的視電阻率曲線Fig．4 Apparent resistivity curve of rotating ellipsoid with low resistance

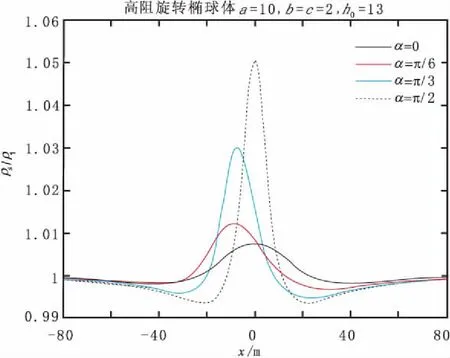
圖5 高阻旋轉(zhuǎn)橢球體的視電阻率曲線Fig．5 Apparent resistivity curve of rotating ellipsoid with high resistance

圖5為高阻旋轉(zhuǎn)橢球體的視電阻率曲線，模型參數(shù)為長軸a=10,兩短軸b=c=2，中心埋深h=13。旋轉(zhuǎn)橢球體分別沿順時針旋轉(zhuǎn)0°、30°、60°和 90°。當(dāng)高阻旋轉(zhuǎn)橢球體水平或直立時，視電阻率曲線關(guān)于中心對稱且直立橢球體的極大值明顯大于水平橢球體。視電阻率曲線的極大值約在異常體頂部附近，兩側(cè)有極小值點。傾向一側(cè)的曲線較緩和而反傾向一側(cè)的曲線較陡峭，隨著傾角α的增大，視電阻率異常變大。

2.2 板狀體的視電阻率曲線特征

板狀體的視電阻率曲線與旋轉(zhuǎn)橢球體的視電阻率曲線的走向大致相同。由于板狀體的b軸趨近無窮大，因此板狀體的視電阻率曲線相比旋轉(zhuǎn)橢球體的曲線更緩和。

圖6為低阻板狀體的視電阻率曲線，模型參數(shù)為長度a=10,厚度c=2，中心埋深h=13。板狀體分別沿順時針旋轉(zhuǎn)0°、30°、60°和90°。當(dāng)?shù)妥璋逅交蛑绷r，視電阻率曲線關(guān)于中心對稱且水平板狀體的極小值比直立板狀體更小；當(dāng)板狀體傾斜時，異常體頂部附近的視電阻率異常為零，在傾向一側(cè)有極小值，在反傾向一側(cè)有極大值。隨著傾角α的增大，視電阻率異常變?nèi)酢?/p>

圖6 低阻板狀體的視電阻率曲線Fig．6 Apparent resistivity curve of plate with low resistance

圖7為高阻板狀體的視電阻率曲線，模型參數(shù)為長度a=10,厚度c=2，中心埋深h=13。板狀體分別沿順時針旋轉(zhuǎn)0°、30°、60°和90°。當(dāng)高阻板狀體水平或直立時，視電阻率曲線關(guān)于中心對稱且直立板狀體的極大值明顯大于水平板狀體，視電阻率曲線的極大值約在板狀體頂部附近，兩側(cè)有極小值點，傾向一側(cè)的曲線較陡峭而反傾向一側(cè)的曲線較緩和。隨著傾角α的增大，視電阻率異常變大。

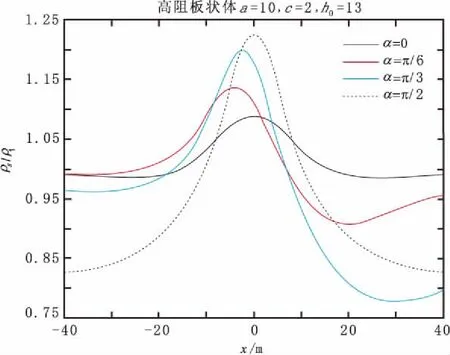
圖7 高阻板狀體的視電阻率曲線Fig．7 Apparent resistivity curve of plate with high resistance

3 結(jié)論

作者首先敘述了國內(nèi)、外對橢球體的視電阻率異常的研究狀況，在此基礎(chǔ)上推導(dǎo)了均勻場中橢球體的電位和視電阻率的公式，得到了傾斜橢球體的視電阻率，并進一步簡化得到板狀體的視電阻率。對傾斜旋轉(zhuǎn)橢球體和板狀體的視電阻率曲線的變化規(guī)律進行了總結(jié)。

旋轉(zhuǎn)橢球體與板狀體的視電阻率曲線的走向大體相似。對于低阻情況，異常體頂部的視電阻率異常為零，在傾向一側(cè)出現(xiàn)極小值，反傾向一側(cè)有極大值，且傾角α越大，極大值越大，隨著傾角α的增大，曲線逐漸變陡；對于高阻情況，視電阻率的極大值出現(xiàn)在異常體頂部，兩側(cè)有極小值，傾向一側(cè)的曲線較緩和而反傾向一側(cè)的曲線較陡峭，隨著傾角α的增大，視電阻率異常變大。

參考文獻：

[1] WEBB J H. The potential due to a buried spheroid[J]. Physical review,1931,38:2056-2067.

[2] 傅良魁,史元盛.論金屬礦電阻率和形狀對ρs異常值的作用規(guī)律[J].桂林冶金地質(zhì)學(xué)院學(xué)報，1981(04)：1-12.

[3] 傅良魁,史元盛. 橢球體電阻率和形狀對其視電阻率異常的影響[J]. 地球物理學(xué)報, 1982,25(04):382-386.

[4] 宋子齊. 橢球類礦體電場和磁場的一般性探討[J]. 長安大學(xué)學(xué)報:地球科學(xué)版,1982(01):88-104.

[5] 雷林源. 論橢球位場函數(shù)的一般形式及其意義 [J]. 桂林工學(xué)院學(xué)報，1982(02):45-51.

[6] 張秋光.場論[M]. 北京：地質(zhì)出版社,1985.

[7] 羅延鐘，張桂青.頻率域激電法原理[M]. 北京：地質(zhì)出版社,1988.

[8] 強建科,何繼善.橢球體上雙頻激電法的正演與反演算法[J].中南大學(xué)學(xué)報:自然科學(xué)版,2007,38(6):1199-1205.

[9] 徐淳寧,魏萍,劉陽.常用場源激勵下橢球體電阻率的數(shù)值計算 [J].長春理工大學(xué)學(xué)報:自然科學(xué)版，2008,31(3):144-146.

[10] 段長生.橢球異常體中梯激電正反演研究[D].桂林：桂林理工大學(xué),2010.

[11] 傅良魁. 電法勘探教程[M]. 北京：地質(zhì)出版社,1980.

[12] 李金銘 .地電場與電法勘探[M].北京：地質(zhì)出版社, 2005.

[13] 段長生,阮百堯,呂玉增,等.任意形態(tài)橢球體中梯激電異常計算[A]. 中國地球物理·2009[C]. 2009:263-264.

[14] 朱佩泓.均勻外電場中的介質(zhì)球和橢球的場[J].宜春學(xué)院學(xué)報,2003,25(02):25-27.

[15] 中南礦冶學(xué)院.金屬礦電法勘探[M].北京：冶金工業(yè)出版社,1980.

[16] 梁昆淼. 數(shù)學(xué)物理方法[M]. 北京：高等教育出版社,1998.