單軸掃頻誘發帆板同步鋼索旋轉振動分析

黃鐵球，閻紹澤

（1.北京交通大學機械與電子控制工程學院，100044北京；2.清華大學精密儀器與機械學系，100084北京）

單軸掃頻誘發帆板同步鋼索旋轉振動分析

黃鐵球1，閻紹澤2

（1.北京交通大學機械與電子控制工程學院，100044北京；2.清華大學精密儀器與機械學系，100084北京）

為明確某帆板面內單軸掃頻力學環境試驗中同步鋼索振動幅度過大和限位結構被破壞的原因，考慮集中質量和限位結構影響，采用有限段方法建立帆板同步鋼索系統的動力學模型，對其在面內單軸掃頻激勵條件的響應進行數值模擬，結果再現了標志點的響應從面內振動發展到面外振動，再到繞兩支撐點軸旋轉振動的復雜振動模式，同時給出限位接觸力和鋼索標志點振幅，仿真結果與試驗狀態吻合.分析表明，持續旋轉振動鋼索施加在限位孔壁上的交變接觸力是導致限位結構破壞的主要原因.

帆板；鋼索；旋轉振動；有限段方法；多體動力學；掃頻激勵

太陽帆板（也稱太陽電池陣或太陽翼）是在軌航天器的典型能源供給裝置.作為航天器的主要附件，其動力學性能的優劣影響著航天器在軌運行的質量.為了減少太陽電池陣展開與鎖定時的多次碰撞與沖擊，以及避免個別關節驅動力不足或失效，需采用一些措施使各塊帆板能同步展開.常用的同步驅動方式是采用繩索聯動機構式（CCL）同步鋼索協同各帆板同步展開.很多國內外學者研究了同步鋼索對太陽帆板動力學性能的影響.如Kumar［1］、王天舒等［2］、閻紹澤［3］等學者，其研究工作主要集中于帆板展開過程的動力學仿真與試驗研究.

太陽電池陣在運輸、發射、飛行和在軌工作等任務過程中經歷振動、沖擊、噪聲等復雜力學環境.火箭發射過程中發動機對衛星及帆板的激勵是最嚴酷的，它是衛星制定振動力學環境的主要依據，其激勵形式往往是寬譜范圍的隨機激勵.雖然火箭發射過程中衛星的振動響應研究很多，但對于同步鋼索自身的振動，無論是在力學環境試驗中還是發射過程中均沒有受到重視，發射過程中的振動狀態更是難以了解.

為了驗證衛星等航天產品是否能夠承受整個工作周期中各種振動環境的考驗，需要在地面對產品進行鑒定和驗收等振動試驗.雖然實際激勵是隨機的，但受制于條件約束，目前正弦掃頻的振動試驗仍是對產品質量進行鑒定和驗收的主要手段［4-6］.

某太陽電池陣產品在地面單軸掃頻振動試驗過程中，同步鋼索出現了非常復雜的動力學響應形態.本文發現并介紹了同步鋼索在單軸掃頻激勵下旋轉運動這一現象，同時，同步鋼索限位結構件出現了明顯的裂紋破損，且同步鋼索中張緊力調節器有劇烈敲擊帆板端面的現象.本文采用有限段方法對含集中質量和限位結構在內的復雜張緊鋼索系統進行了動力學建模，借助Adams軟件形成數學方程并進行數值積分，再現了同步鋼索在單軸掃頻激勵下出現的旋轉運動模式，并對試驗過程中出現的限位結構件破壞和調節器敲擊帆板等事故給出合理解釋，為產品改進提供了重要依據.

1 單軸掃頻激勵誘發的同步鋼索旋轉振動現象

太陽翼展開同步鋼索的兩端纏繞在固定同步輪上，靠近一端的位置布置有一個張緊力調節器，依靠調節器可將鋼索張緊到所需張緊力.同時，中間位置有一限位孔，以防止同步鋼索的振動幅度過大.鋼索與太陽翼試驗裝置及其示意圖如圖1、2所示.

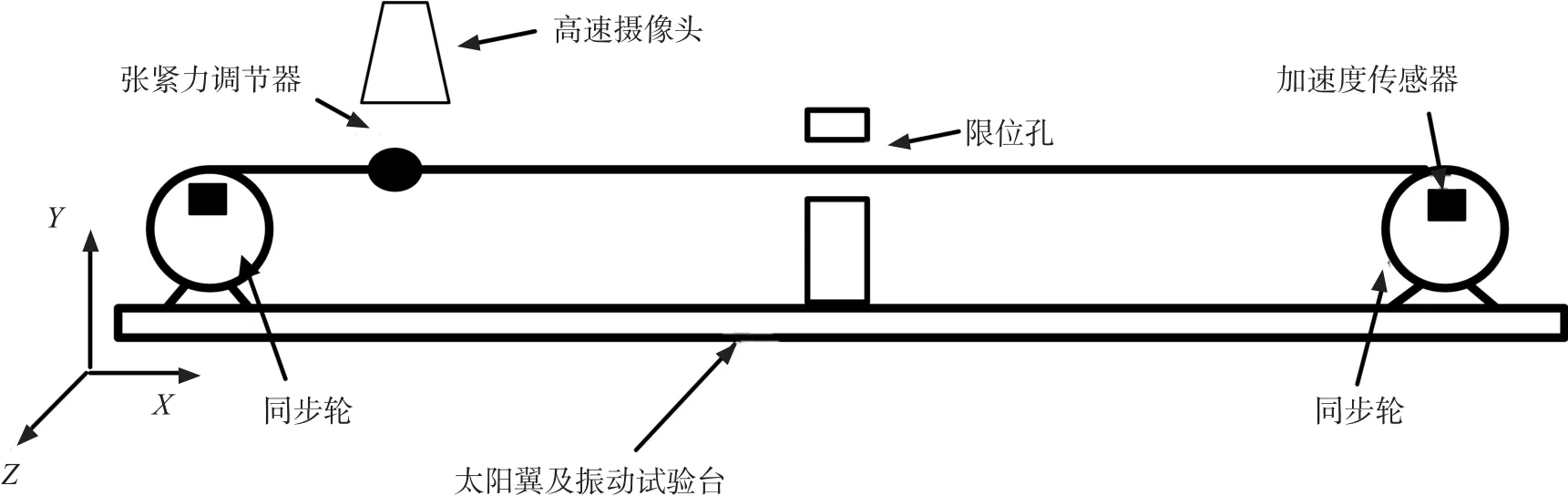
圖1 試驗裝置

圖2 同步鋼索與太陽翼安裝圖

試驗過程中振動臺對太陽翼進行掃頻激勵，掃頻范圍為5.0～100.0 Hz，激勵方向沿圖示坐標系Z方向.利用高速攝像機對鋼索振動情況進行記錄，同時采用加速度計記錄鋼索兩端固定點的加速度值.張緊力調節器為集中質量，其振幅較大.為了保護調節器裝置，將調節器用白色膠紙包裹.圖3給出了不同激勵頻率下錄像得到的鋼索振動情況.

觀察白色包裹后調節器中部的軌跡發現，從8.0～26.0 Hz進行掃頻時，鋼索和調節器的振動基本在一個平面內，但振幅隨掃頻的頻率上升逐漸增大.白色調節器右端面影像軌跡基本是直線，據此可以判斷調節器的振動為與鋼索垂直面內的“往復”式橫向振動.

從40.0～56.0 Hz掃頻結果來看，調節器“振幅”逐漸增大，且白色調節器右端面影像已經不再是直線，而是呈現出清晰的圓周型弧線，這預示著鋼索出現了一種特殊的振動模式——“旋轉振動”，這種振動模式類似于“跳繩運動”.此時，鋼索上任何點的振動不再是平面內的“往復”運動，而是鋼索垂直平面內的近似“圓周”運動.這一振動模式是在26.0～40.0 Hz之間掃頻激勵逐漸發展形成的.掃頻到65.0 Hz時，可看到鋼索振幅減小到很小，振幅已不明顯.這意味著從62.0～65.0 Hz的短暫掃頻過程中，劇烈的旋轉振動突然消失.

同時，在試驗過程中發現兩個問題：一是調節器有劇烈而清脆的敲擊帆板端部現象；二是某限位孔結構件出現裂紋破壞現象.該試驗過程中調節器的響應幅值和限位孔接觸力大小有待研究.

圖3 張緊力調節器振動錄像記錄

2 同步鋼索系統動力學建模

為了對同步鋼索的奇特動力學行為有深入了解，并對被破壞限位結構件受力及調節器敲擊帆板端部原因進行準確分析，為產品改進設計提供準確依據，需要對同步鋼索系統在掃頻激勵下的動力學行為進行深入研究.

同步鋼索可以看作是兩端張緊的弦系統.關于弦的動力學行為的研究是比較豐富的［7～16］，最具代表性的是Reilly等［11］對于標準張緊弦在面內簡諧激勵下的面外運動的詳細研究.上述研究均是針對均勻一致弦索來開展的.

帆板同步鋼索系統相對上述研究的對象而言，有兩點結構上的重要不同：一是同步鋼索包含有張緊力調解器，該調節器可簡化為弦上的集中質量；二是同步鋼索系統中為了約束較長鋼索的擺動，中間往往布置有一個或多個限位孔，當鋼索的擺動幅度大于孔徑時，限位孔與鋼索接觸，對鋼索擺動起到限位的作用.由于同步鋼索系統存在集中質量和限位接觸的作用，推導其非線性振動的理論公式并求其解析解是較難的.基于有限段方法在柔性繩索動力學精細建模上的大量應用［8-9］，本文借助多體動力學中的有限段方法來對同步鋼索系統進行建模和仿真研究.

有限段方法的基本思想是將連續的單個物體，離散為多個子單元，將質量和轉動慣量按照幾何和分段規律分配到各個子物體上，子單元的柔性特征等效到其節點處，即將“柔軟”的子單元等效為多個“剛性段”與“柔性連接”的離散化系統，從而實現對復雜變形物體的動力學建模.采用有限段方法，無論物體多么“柔軟”，理論上只要離散的段足夠多，連接關系足夠準確，總是可以以給定計算精度逼近真實狀態的.

2.1 同步鋼索的有限段模型

將同步鋼索等分離散成N個剛性段，段與段之間采用彈簧阻尼器連接．取其中任意段i，如圖4所示，其中，Oi為i段質心位置，在i段上該點沿慣性主軸建立坐標系Oi-χiyizi，Ri為i段質心在慣性系下的位置矢量．Pi、Qi分別為該段兩端彈性力的作用點，Ti和Ti＋1分別為第i-1段和第i＋1段對其作用的彈性連接力矢，由于同步鋼索張緊力遠遠大于重力，可忽略重力的影響．該段為典型的自由剛體，采用牛頓定律可得到其平動的動力學方程為

我國常規天然氣儲量相對煤炭資源偏低，但非常規天然氣儲量和開發潛力較大。我國頁巖氣探明儲量高達134.4萬億立方米，按可采資源量預計可達到世界第一。2016年，我國頁巖氣產量為80億立方米，同比增長68%，居世界第三位；煤層氣產量為50億立方米，煤制氣產量為17億立方米。通過開發國內非常規天然氣，同時加大管道氣、 LNG的引進，可充分保障我國天然氣供應。

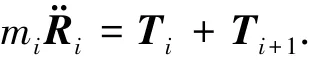
式中mi為i段的質量．

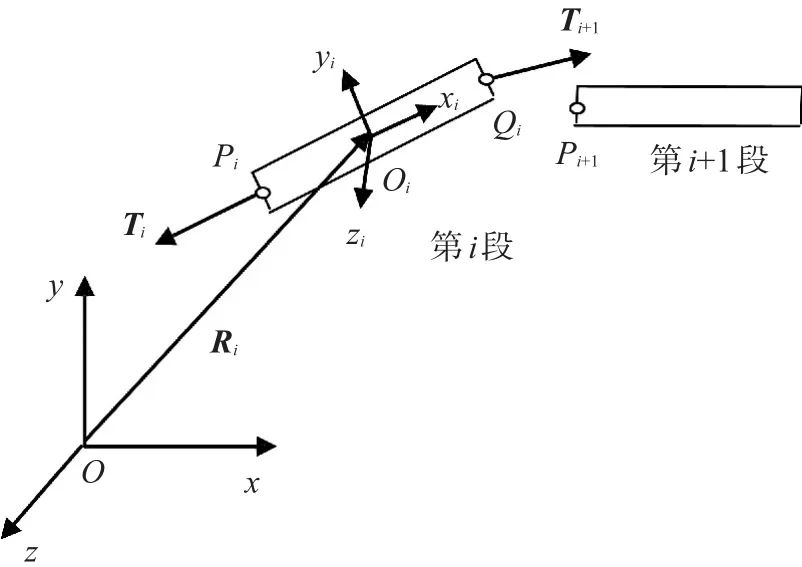
圖4 任意段的受力圖

運用歐拉轉動動力學方程，可得到i段轉動的動力學方程如下：

式中：Ii為主慣量對角陣，ω·為繞質心坐標系的轉動角加速度矢量，si為質心到Pi的位置矢量，si＋1為質心到Qi的位置矢量．

令li＋1為由Qi指向Pi＋1的位置矢量，.li＋1為相應速度矢量．彈性連接力矢可寫為

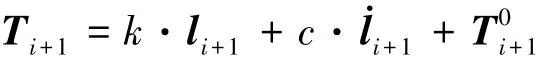
式中，k為連接剛度，由段長度、弦索拉伸彈性模量和截面積決定；c為阻尼；為預緊力項．

第一段與最后一段同樣通過彈性力與慣性系連接．在慣性系上的連接點為Q0、Plast，其位置不變，速度為零．

張緊力調節器作為其一個有限段，賦予相應的質量、轉動慣量特性，即可實現集中質量的建模.

2.2 限位孔接觸力模型

鋼索與護座接觸時，護座給鋼索的力可以分解為y和z兩個方向，令其為Fy、Fz，接觸力模型簡化為彈簧模型，給定的接觸力如下：

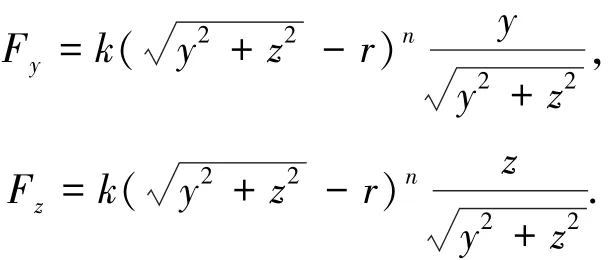
式中：k為接觸剛度，n為接觸剛度的冪級數，y、z分別為鋼索相對限位孔在接觸面內的位移，r為限位孔半徑與鋼索半徑之差．

依照上述方法建立每個子段的動力學方程，聯立可得到整個系統的動力學方程組，借助現有多體動力學方法可快速組裝動力學方程，通過數值積分可得到弦索上各點的運動特性.經典弦索振動力學模型的基本假設中，要求弦索橫向振動的幅度較小，即弦索上任意點切線的傾角都很小，而基于多體動力學的有限段方法沒有這個假設條件的限制.

3 仿真結果

以上述力學模型為依據，利用Adams軟件對試驗中的帶集中質量的鋼索進行分段建模.模型鋼索長2 m，分段數量200段，單段質量0.038 8 g，調節器質量10 g，連接剛度18 760 N／mm，阻尼0.5 N·s／mm，鋼索預緊力40 N.限位孔與鋼索間隙1.5 mm，接觸剛度400 N／mm.對鋼索在單向掃頻激勵條件下的響應進行數值模擬.激勵方向為圖1中坐標系Z向，掃頻激勵從20.0～80.0 Hz.太陽翼振動試驗過程中測量得到同步輪的加速度響應，該響應作為鋼索的加速度激勵輸入，對測量的同步輪標志點加速度響應進行平整，得到如圖5所示的加速度激勵波形作為仿真模型的激勵輸入.

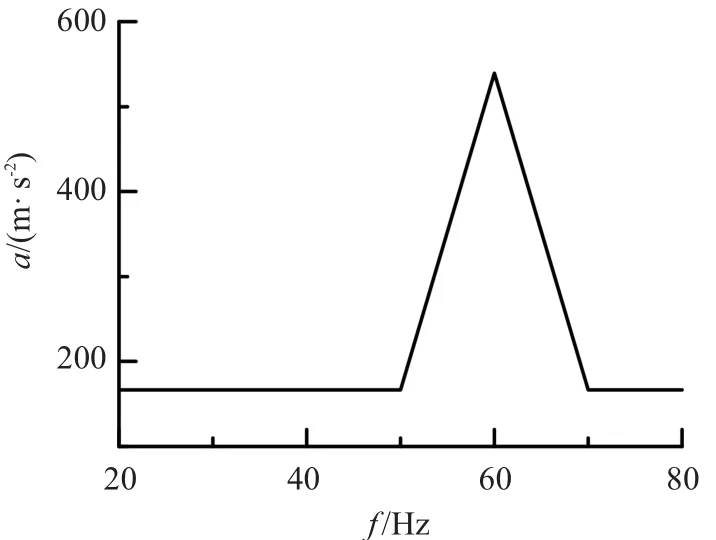
圖5 激勵頻域波形

試驗時，實際的激勵時間往往達到數分鐘，這樣長時間的數值仿真數據規模很大，在保證響應時間充分的條件下本仿真將激勵時長壓縮到12 s，對應的加速度激勵時域函數設計如下：

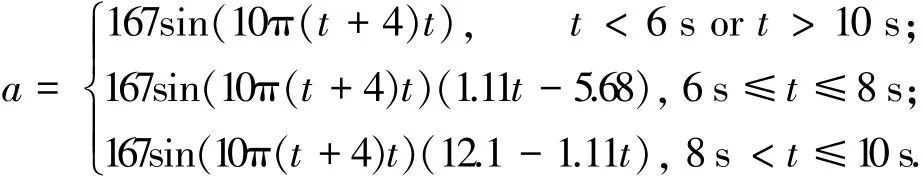
圖6為標志點的時域響應曲線.由圖6可看出，在掃頻激勵作用下，標志點響應幅值逐漸增大，在激勵頻率約為66.0 Hz時達到最大，然后迅速衰減.標志點響應最大幅值達到38 mm，而鋼索離帆板端面的距離約為30 mm，因此試驗中調節器出現了敲擊帆板的現象.

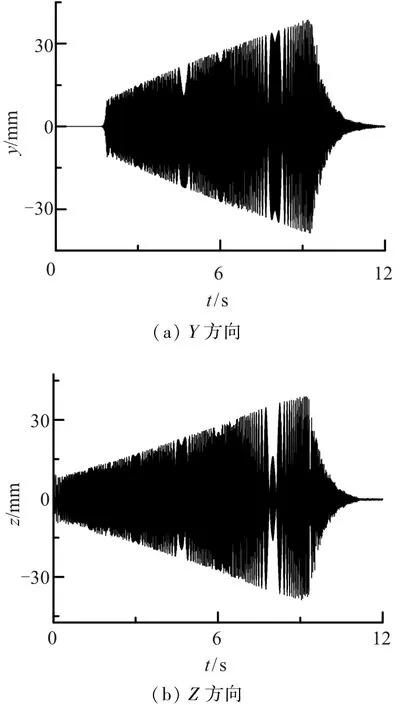
圖6 標志點響應曲線

圖7 為掃頻過程中調節器上標志點在YZ平面（與鋼索縱軸即X軸垂直的平面）內的運動軌跡.圖7（a）、（b）表明在20.0～26.0 Hz內標志點的運動軌跡基本為直線，即標志點在XZ平面內振動.隨著激勵頻率的增加，從28.0～30.5 Hz的掃頻過程中，標志點的運動軌跡線從直線形式開始迅速轉變為近似圓周的軌跡，如圖7（c）所示，這表明鋼索產生了旋轉運動.從30.5～72.0 Hz掃頻范圍內，經歷了近似圓周軌跡半徑逐漸增大，再到圓周半徑逐步縮小的振動過程，見圖7（c）～（f）.由圖7的數值模擬結果可以看出，在面內單方向掃頻激勵下標志點的響應從面內振動，逐漸發展到面外振動，再到繞兩支撐點軸的旋轉運動，振動幅度由小變大，再由大變小的過程，與圖3所示的試驗結果是基本吻合的.另外，該旋轉振動模式沒有線性系統意義下的共振點，其振幅在掃頻激勵下能長時間持續增大.

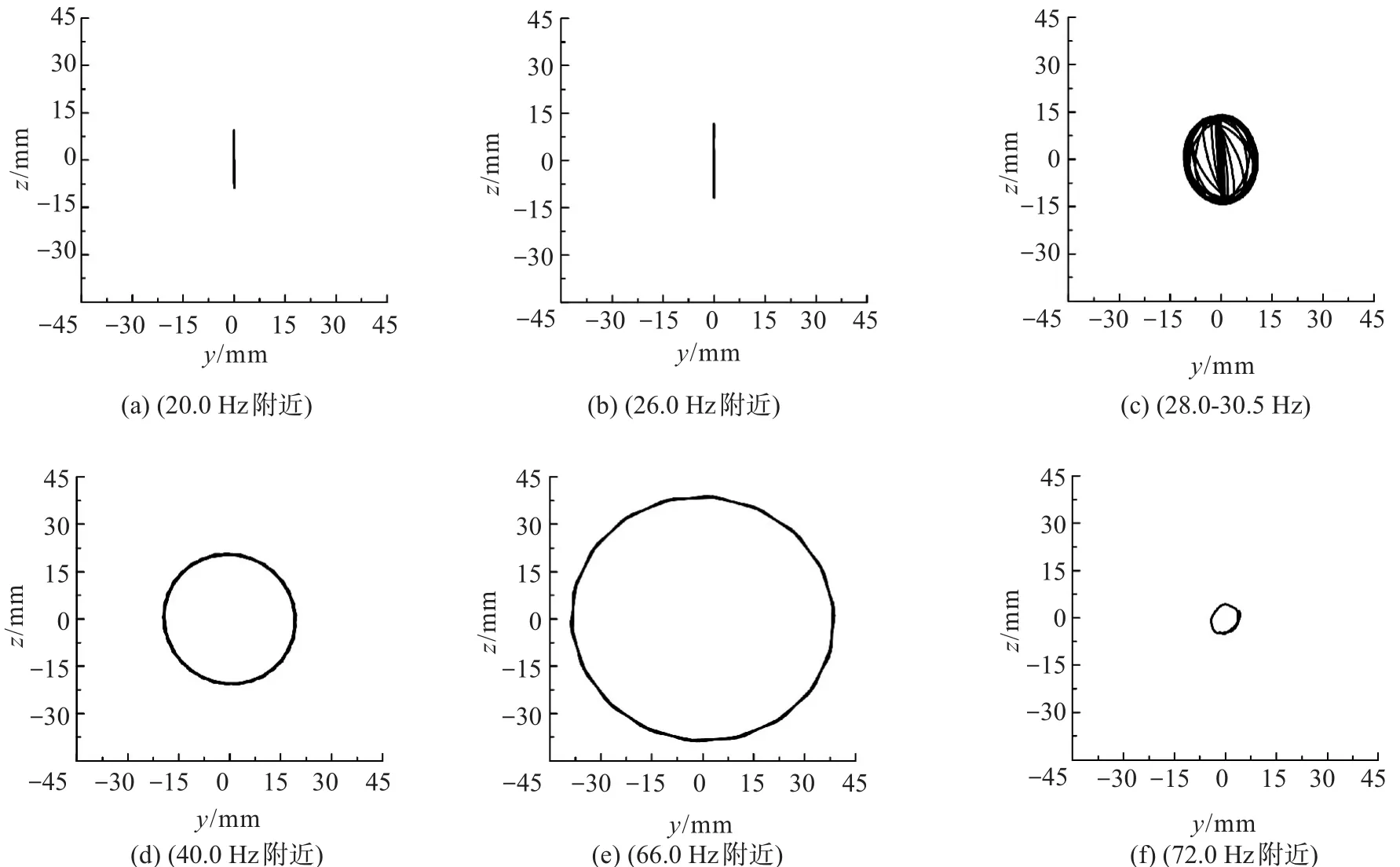
圖7 掃頻過程中調節器上標志點在YZ平面內的運動軌跡

圖8 為鋼索與限位孔的接觸力.由圖8可以看出，由于旋轉振動的持續存在并不斷加劇，鋼索與限位孔接觸力也持續增大，仿真中最大值達到了近60 N.另外，由于鋼索的旋轉運動形式導致該力為繞限位孔圓周持續作用的交變循環力.在接觸力持續作用這一點上，旋轉振動與往復振動的效果是有著本質區別的.往復振動往往只是在共振點上激起較大的響應，一旦激勵頻率越過了共振點，其響應很快衰減，結果是鋼索與限位孔接觸力僅5 N以內（圖8中0～1 s）或甚至無接觸（圖8中11 s后）.但是，旋轉振動使得該接觸力變成了較長時間的持續作用（圖8中1.6 s～9 s）.

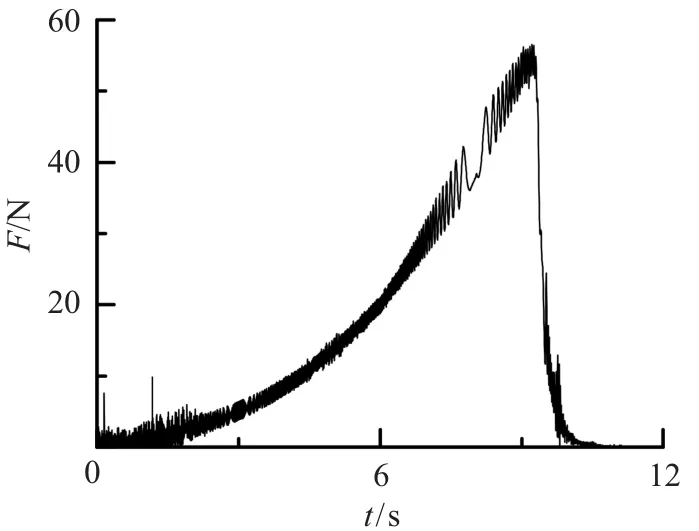
圖8 限位孔接觸力

振動試驗中，由于該掃頻作用的時間長達數分鐘，且試驗進行了多次，限位結構件實際接觸力交變循環次數超過60 000余次.并且，由于減重的需要，限位結構件采用的是工程塑料，其疲勞許用應力不高.依據該載荷進行的疲勞計算表明，限位結構件可在此條件下疲勞破壞.

4 結 論

1）在帆板掃頻激勵振動試驗中，首次發現帆板同步鋼索在單軸掃頻激勵下誘發了的旋轉運動狀態，并且限位結構出現裂紋破壞，同時張緊力調節器劇烈敲擊帆板端面.

2）考慮集中質量和限位結構對張緊鋼索系統的影響，采用有限段方法建立該類鋼索系統的動力學模型，并進行了數值模擬.

3）仿真結果準確再現了在面內單軸掃頻激勵下，系統響應從面內振動，逐漸發展到面外振動，再到繞兩支撐點軸的旋轉運動，振動幅度由小變大，再迅速衰減的過程.

4）由于掃頻激勵可以激起鋼索系統持續大幅度的旋轉振動，從而形成持續交變循環的限位接觸力，該類型接觸力是限位結構破壞的最重要因素.持續旋轉振動所帶來的振幅持續增加也是鋼索敲擊帆板端面的重要原因.

5）雖然有限段方法在模擬該類弦索系統旋轉振動響應上被證明是準確有效的，但單軸掃頻激勵下旋轉振動出現的條件仍不甚清楚.其產生機理和量化試驗均有待繼續深入研究.

［1］KUMAR P.Deployment and retraction of a cable?driven rigid panel solar array［J］.Journal of Spacecraft and Rockets，1996，33（6）：836-842.

［2］王天舒，孔憲仁，王本利，等.太陽帆板繩索聯動同步機構的機理和功能分析［J］.宇航學報，2000，21（3）：29-33，38.

［3］閻紹澤，蔡仁宇，丁袆，等.基于ADAMS的太陽電池陣動力學模擬參數化建模系統［J］.電子機械工程，2011，27（3）：18-23.

［4］王萍萍，陳昌亞，羅文波，等.衛星振動試驗中頻漂現象分析［J］.哈爾濱工業大學學報，2006，38（1）：74-75，80.

［5］劉沫，馮咬齊，何玲.衛星產品多軸隨機振動試驗條件制定方法初探［J］.航天器環境工程，2013，30（2）：155-159.

［6］邢天虎.力學環境試驗技術［M］.西安：西北工業大學出版社，2003：216-253.

［7］金棟平，文浩，胡海巖.繩索系統的建模、動力學和控制［J］.力學進展，2004，34（3）：304-313.

［8］楊志軍，馮文賢，陳新.非線性索單元等效多體動力學模型研究［J］.中國機械工程，2011，22（3）：262-264.

［9］RUBIN M B，GOTTLIEB O.Numerical solutions of forced vibration and whirling of a non?linear string using the theory of a cosserat point［J］.Journal of Sound and Vibration，1996，197（1）：85-101.

［10］ZHOU Xiaodong，YAN Shaoze，CHU Fulei.In?plane free vibrations of an inclined taut cable［J］.Journal of Vibration and Acoustics，2011，133（3）：031001.

［11］REILY O O，HOLMES P J.Non?linear，non?planar and non?periodic vibrations of a string［J］.Journal of Sound and Vibration，1992，153（3）：413-435.

［12］TAKAHASHI K，KONISHI Y.Non?linear vibrations of cables in three dimensions，Part I：Non?linear free vibrations［J］.Journal of Sound and Vibration，1987，118（1）：69-84.

［13］TAKAHSHI K，KONISHI Y.Non?linear vibrations of cablesinthreedimensions，partII：out?of?plane vibrations under in?plane sinusoidally time?varying load［J］.Journal of Sound and Vibration，1987，118（1）：85-97.

［14］BENEDETTINI Y，REGA G.Numerical simulations of chaotic dynamics in a model of an elastic cable［J］. Nonlinear Dynamics，1991（1）：23-38.

［15］LIN Bisen，RAVI?CHANDAR K.An experimental investigation of the motion of flexible strings：whirling［J］.Journal of Applied Mechanics，2006，73：842-851.

［16］DEMENTBERG M F，LOURTCHENKO D V.Transition from planar to whirling oscillations in a certain nonlinear system［J］.Nonlinear Dynamics，2000，23：165-174.

（編輯 楊 波）

Whirling response analysis of a cable on solar array under single?axial swept frequency excitation

HUANG Tieqiu1，YAN Shaoze2

（1.School of Mechanical，Electronic and Control Engineering，Beijing Jiaotong University，100044 Beijing，China；2.Dept.of Precision Instruments and Mechanology，Tsinghua University，100084 Beijing，China）

To find the reason of limiting hole fracture and over?expected vibration amplitude on the mechanical environmental test to a Close Cable Loop（CCL）under only single?axial inner?plane swept frequency excitation，the finite segment method of multi?body dynamics was introduced to model and simulate the cable system with a concentrated mass and a position limiting hole，the cable vibration response and the contact force in limiting hole were obtained.The results showed that the vibration response started from inner?plane vibration to outer?plane vibration and to continuous rotational vibration.Cable vibration amplitude enhanced continuously due to rotational vibration process，and attenuated suddenly.The response process and vibration amplitude was coincided with the test.Continuous rotational vibration under swept frequency excitation is the key reason for the problem of fractures.

solar panel；steel string；rotational vibration；finite?segment method；multi?body dynamics；swept frequency excitation

V415.4

：A

：0367-6234（2014）11-0070-06

2013-11-14.

中央高校基本科研業務費專項資金（2011JBM105）.

黃鐵球（1971—），男，博士，講師；閻紹澤（1964—），男，教授，博士生導師.

黃鐵球，tqhuang＠bjtu.edu.cn.