復合材料汽車板簧的優化設計

趙燕 蔡艷濤 王聲濤 李宇菲 鄭銀環

（武漢理工大學機電工程學院）

隨著汽車平順性和節能環保要求的提高，對汽車輕量化的要求越來越高。汽車鋼板彈簧的質量約占整車質量的5%～7%，因此鋼板彈簧的輕量化對汽車的輕量化有十分積極的影響。傳統鋼板彈簧的設計，國內外學者進行了很多的研究并提出了很多優化和可靠性的設計方法[1-4]。纖維增強復合材料具有單向強度高、單位質量儲能大、彈性模量小及耐腐蝕等優點，所以近年來科研人員開始致力于復合材料板簧的研究[5-7]。文章對復合材料板簧進行優化設計并與相同條件下的鋼板彈簧進行對比，結果表明，復合材料板簧的性能優于鋼板彈簧。

1 復合材料汽車板簧的優化設計

根據復合材料層合板力學的相關理論，對復合材料板簧進行優化設計。選擇適合汽車板簧的復合材料并設計計算板簧的尺寸以便選取合適的設計變量，以最小的板簧質量為目標函數，以板簧的尺寸參數為設計變量，以板簧的強度和剛度為約束條件，建立復合材料汽車板簧的優化數學模型。最后結合某車型板簧的原始數據，調用Matlab 優化工具箱中的有約束非線性優化函數求得板簧最小質量下的最佳尺寸，為板簧模型的建立和有限元分析奠定基礎[8-10]。

1.1 板簧材料的選擇

目前，國內外復合材料板簧所用材料主要是E- 玻璃纖維增強樹脂基復合材料（Glass fiber reinforced plastics，GFRP）。該材料符合汽車板簧的力學性能要求，且制造工藝成熟、成本低，滿足輕量化要求，故文章采用E- 玻璃纖維。考慮到復合材料汽車板簧的受力特點和工況，其樹脂基體要在靜載荷與動載荷作用下工作并能吸收振動，文章所選基體材料為環氧樹脂，對某車型的主副簧復合式板簧進行研究，主簧為2 片，副簧為1 片，利用E- 玻璃纖維環氧樹脂來取代彈簧鋼。

1.2 板簧的尺寸設計計算

為了使板簧各片的疲勞壽命大致相同，在確定各片的長度時，應盡量使應力沿著長度方向合理分布，文章采用計算法來確定板簧各片的長度。

如圖1所示，第i 片板簧的彎曲應力沿片長的分布有3 種情況。圖1中，s 為板簧在夾緊時2 個騎馬螺栓（或稱U 形螺栓）的中心距；σi/Pa 為板簧在中心螺栓夾緊處的應力；σxi/Pa 為與下一片板簧的端部相接觸處的應力。

理論上圖1c 的應力分布是最合理的，因為能保證板簧的葉片在長度方向上強度相等，充分利用了材料，但由于卷耳處與車架聯接后在使用中能產生附加應力（如扭轉應力），所以主片的疲勞壽命能降低；圖1b 所示的應力分布情況只有在特殊條件下才能使用，如為了補償騎馬螺栓或中心螺栓夾緊板簧時產生的預應力；圖1a 所示的應力分布可以使主片卷耳處的附加應力與本身的應力相加后和中心螺栓處的應力大致相等，所以圖1a 的應力分布較為合理，文章采用這種應力分布。

圖1中，令:γi=σxi/σi，γ 稱為應力分布系數，則3 種情況下的值分別為 γ＜1，γ＞1 和 γ=1。表1示出γ的推薦值。

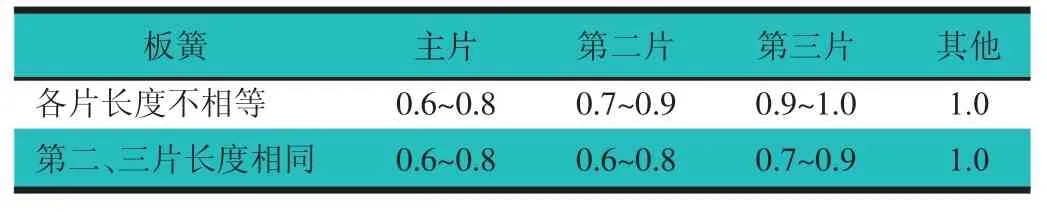
表1 應力分布系數（γ）推薦值

1.2.1 主簧的尺寸設計

每片主簧的長度和片端部的受力情況，如圖2所示。

對于第一片主簧（圖2中i=1），從P1～P2為懸臂梁，在P2處的力矩平衡，結合圖1a 和圖2的受力分析，可列出如下方程:

由此可得:

已知板簧根部的彎曲應力最大，所以可得:

式中:l1，l2——第一、二片板簧從中心螺栓到片端部的長度，mm；

σ1——第一、二片板簧從中心螺栓到片端部的應力，N；

P1，P2——第一、二片板簧端部的載荷，N，其中P1為已知力，即作用在第一片簧卷耳上的力；

W1——第一片板簧從中心螺栓到端部的截面系數，mm3；

γ1——第一片板簧的應力分布系數；

s——U 形螺栓的中心距，mm。

文章取γ=0.7，代入原始數據（原始數據在后文）可初步估算得:

1.2.2 副簧的尺寸設計

當板簧承受較小的載荷時，只有主簧工作，隨著載荷不斷地增加，副簧也開始工作，假設主副簧剛開始接觸時的載荷為Pi，主副簧完全接觸時的載荷為Pj，則需要滿足式（3）:

式中:i——伸直時副簧與主簧的長度比，i=l3/l1。

從式（3）可見，Pj和Pi的比值與主簧和副簧的長度比有關。

由式（3）可初步估算得:i=0.634 4，l3=0.634 4l1。

1.3 板簧的優化設計

板簧優化設計的目標函數為板簧的質量，并以主簧第一片的長度和主副簧的厚度為設計變量，以空載和滿載載荷下板簧的剛度和各片的強度為約束條件，得到板簧最小質量下的最佳尺寸。該問題為不等式約束條件的非線性優化問題。

某車型的板簧原始參數如下:空載載荷Q1=2P1=2 200 N，滿載載荷Q2=2P2=7 800 N，主副簧剛開始接觸時的載荷Pi=1 700 N，主副簧完全接觸時的載荷Pj=4 650 N，第一片板簧的伸直長度L=2l1=978 mm，s=100 mm，主簧每片厚度h1=6 mm，副簧厚度h2=7.5 mm，板簧寬b=60 mm，原鋼板彈簧總成質量m=9.05 kg，空載載荷下板簧剛度的期望值滿載載荷下板簧剛度期望值設計允許誤差η=0.4%。

板簧材料的剛度系數Q11=39.17GPa，Q12=Q21=2.18GPa，Q22=8.39 GPa，Q66=4.14 GPa，縱橫向拉伸極限應力分別為Xt=1 062 MPa，Yc=118 MPa，體積質量 ρ=1.8 g/cm3，安全系數取n=3。x，y，z 方向失效拉伸應力分別為Ex=34000MPa，Ey=6 530 MPa，Ez=6 530 MPa；xy，xz，yz 方向失效剪切應變分別為 Pxy=0.217，Pxz=0.217，Pyz=0.366；xy，yz，xz 方向失效剪切應力分別為 Gxy=2 433 MPa，Gyz=1 698 MPa，Gxz=2 433 MPa。

用Matlab 優化后得到的結果，如表2所示。

表2 板簧優化設計結果

2 板簧的靜態有限元分析

通過板簧的靜態有限元分析來研究其靜態力學行為，從而驗證板簧優化結果及模型建立的正確性。在得到板簧優化設計的結果后，將板簧的Pro/E 三維幾何模型導入ANSYS 中，在前處理器中選擇單元類型，定義實常數和材料參數，做布爾運算、劃分網格及設置接觸對后，進行板簧裝配，然后分析滿載載荷下的變形和應力，并計算滿載剛度。

2.1 板簧的三維實體建模

根據1.3 節對板簧模型的優化結果，建立Pro/E 模型，如圖3所示，板簧的有限元模型，如圖4所示。

2.2 板簧裝配仿真結果

圖5示出板簧總成在中心螺栓夾緊后的預應力分布圖。由圖5所示可知:裝配預應力主要出現在主簧的中央和主簧第二片兩側，且預應力對稱分布。裝配預應力的最大值為284 MPa，位于主簧第一片的下表面；其次為主簧第二片的兩側，預應力范圍是189～252 MPa，其他部位預應力較小。

2.3 滿載下應力分析及靜剛度計算

2.3.1 滿載下的應力分析

在完成板簧裝配預應力的分析后即可進行滿載載荷下的靜力分析。在主簧第一片兩端施加垂直載荷，每個節點加780 N，左右兩端總共10 個節點，所以板簧受到的總載荷為7 800 N，圖6示出應力分析結果。

從圖6可以看出，在滿載情況下，應力的最大值為429 MPa，位于主簧第一片的下表面中央和主簧第二片的上表面中央；其次為主簧第二片靠近兩端處，應力的值為333～381 MPa，左右兩端呈對稱分布。副簧由于未與主簧完全接觸，此時的應力值為95～143 MPa。板簧的極限應力值為1 062 MPa，遠大于滿載載荷下的最大應力值，所以在滿載載荷作用下板簧應力滿足要求。

2.3.2 板簧的靜剛度計算

圖7示出板簧總成在滿載載荷下位移分布圖。由圖7可知，主簧第一片自由端向下的位移量為28.26 mm，減去其在裝配過程中的預變形量-18.01 mm，在加載過程中主簧第一片的自由端向下的位移量為46.27 mm，即板簧的靜撓度為46.27mm，所以滿載剛度為168.58N/mm，而滿載期望的剛度為146 N/mm，有限元計算的剛度值偏大，主要是由于接觸對設置的誤差所致。由2.2 節裝配過程的仿真結果可知，板簧總成在裝配夾緊后的弧高為144 mm，所以滿載狀態下的弧高為97.73 mm。

仿真分析結果表明，板簧在裝配過程中各片中部相互貼緊，上片的曲率半徑會減小，而下片的曲率半徑會變大，裝配后中心螺栓附近的應力最大；在滿載工作載荷的作用下，片端會產生沿工作載荷方向的位移，該位移在一定范圍內與工作載荷的大小成正比。

3 板簧的動特性仿真分析

板簧在實際使用過程中，經常受到路面的動態激勵。本節研究板簧在正弦載荷作用下片端的位移響應和動剛度，并進行疲勞壽命的仿真分析，預測板簧的疲勞壽命。

3.1 板簧的動剛度分析

在板簧中部施加約束，在其端部施加正弦力:F1=5 000+2 800sin（2πt）。由于板簧模型左右對稱，則板簧每端的動載荷為F2=2 500+1 400sin（2πt）。而每端有 5 個節點，所以每個節點上施加動載荷為F3=500+280sin（2πt）。

根據文獻[11]，考慮摩擦情況的影響，并取摩擦系數為0.2。

分析過程中分2 個載荷步加載，第1 個載荷步模擬中心螺栓夾緊板簧的裝配過程，第2 個載荷步模擬板簧在端部受正弦載荷作用下的響應過程。

求解完成后，在時間歷程后處理器中選取片端3751 號節點z 方向的位移，生成位移隨時間的響應曲線，如圖8所示。

由圖8可知，在前1 s 時間內，由于中心螺栓的夾緊，板簧第一片曲率半徑減小，片端會向上移動。由于定義z 軸的正方向是垂直板簧向下，所以圖8中曲線在前1 s 是下降的，完全裝配夾緊后z 方向的位移量是-17.195 mm，即夾緊過程使片端向上移動17.195 mm。在后1 s 時間內，板簧片端加的正弦力，由于各片間存在摩擦且考慮到裝配過程中的預應力效應，片端位移按近似正弦規律曲線變化，最大值為26.74 mm，最小值為0.91 mm。

在正弦載荷作用期間，片端的位移量減去裝配夾緊后z 方向的位移量-17.195 mm，即可得到正弦載荷作用下的撓度，如表3所示。

表3 板簧載荷與撓度關系表

表3的數據在Matlab 中進行曲線擬合后得到動態載荷增加和減少過程中動剛度曲線，如圖9所示。

從圖9可知，加載階段的剛度曲線在卸載階段的剛度曲線上方，即加載階段的剛度（172 N/mm）大于卸載階段的剛度（166 N/mm）。加載過程與卸載過程有差別，大小相同的載荷在加載階段的撓度要小于卸載階段的撓度。

3.2 板簧的疲勞壽命仿真分析

對于板簧而言，疲勞壽命指的是任何一片板簧最先產生宏觀裂紋時的循環次數，而宏觀裂紋指的是簧片某一個位置的兩個側面沿厚度方向的裂通。

3.2.1 板簧疲勞危險區域的確定

文章中板簧在由中心螺栓夾緊的過程中，最大應力處出現在第一、二片簧中間段的上下表面處，所以選主簧中間段中心螺栓附近為疲勞危險區域。

在 F1=5 000+2 800sin（2πt）的作用下，板簧發生變形，當載荷達到7 800 N 時和載荷在2 200 N 時的應力分布，如圖10所示。

從圖10a可以看出，在正弦力處于最大值的時刻（板簧載荷為7 800 N），應力最大值為429 MPa 出現在主簧中間段中心螺栓附近，此處的節點號為1658；在交變載荷處于最小值的時刻（板簧載荷為2 200 N），應力最大值為342 MPa，還是出現在主簧中間段中心螺栓附近，節點號仍為1658，如圖10b所示。因此應力幅為43.5 MPa。

在ANSYS 中通過通用后處理POST1 當中的列表選項可得節點號為1658 的節點在交變載荷最小和最大時各個方向的應力值，如表4所示。

表4 板簧危險區域1658 號節點應力值 Pa

3.2.2 板簧的疲勞壽命仿真分析過程及結果

在ANSYS 的疲勞計算模塊當中，疲勞計算的節點位置數可以大于5 個，事件數可取10 個，每個事件可取3 種載荷。本次疲勞試驗仿真分析當中疲勞位置取1 個，疲勞事件取1 個，載荷取2 個。

根據文獻[12]給出的E- 玻璃纖維環氧樹脂的S-N曲線圖，找出一系列關鍵點并確定關鍵點的近似坐標值，輸入ANSYS 的疲勞分析模塊，定義循環次數為30 萬次，激活疲勞壽命運算器后，得到板簧的疲勞計算結果，如圖11所示。

由圖11可見，疲勞分析的仿真結果是5 000 萬次。實際工程應用中零部件通常取200 萬次作為理論上的無限次循環，所以該仿真結果可認為是無限次。

4 結論

文章利用Matlab 中的相關優化函數對板簧結構進行了優化設計，結果表明:優化后的板簧質量比優化前減少了50%。建立了板簧模型，進行了滿載載荷下的靜力分析。結果表明:在滿載工作載荷的作用下，片端會產生沿工作載荷方向的位移，該位移在一定范圍內與工作載荷的大小成正比，仿真計算所得滿載剛度值與設計要求剛度值接近，而滿載載荷下的應力最大值仍出現在中心螺栓附近。仿真結果基本與實際情況相符。

在正弦載荷的作用下，分析了板簧端部的位移隨時間的響應，計算了動剛度，然后進行了疲勞分析，預測板簧的疲勞壽命。結果表明，在正弦載荷的作用下，位移隨時間的響應按照近似正弦函數的規律變化；由于板簧片間存在摩擦，在加載階段的剛度大于卸載階段的剛度；疲勞壽命的仿真結果為5 000 萬次，即實際工程應用中的無限次。