復雜網(wǎng)絡(luò)中節(jié)點重要度的一個評估指標

蔣豐景，陳玥琪

(西安電子科技大學理學院，陜西西安710071)

復雜網(wǎng)絡(luò)中節(jié)點重要度的一個評估指標

蔣豐景，陳玥琪

(西安電子科技大學理學院，陜西西安710071)

為了簡單而有效地評估網(wǎng)絡(luò)拓撲結(jié)構(gòu)中各節(jié)點重要性，本文基于節(jié)點的連接度和局部連通性，定義了一個節(jié)點重要度函數(shù).該重要度函數(shù)指標實質(zhì)上與網(wǎng)絡(luò)中的平均最短距離指標是一致的，通過該重要度函數(shù)指標值的大小可以得到網(wǎng)絡(luò)中各節(jié)點的重要度排序.理論分析與實例表明，對于小型網(wǎng)絡(luò)，該方法的計算比較簡單，且直觀、有效、合理.

節(jié)點重要度;鄰居節(jié)點;節(jié)點刪除;平均最短距離

隨著信息技術(shù)飛速發(fā)展，互聯(lián)網(wǎng)已成為社會輿論傳播的主要載體之一，無論是現(xiàn)實生活還是系統(tǒng)科學，都與網(wǎng)絡(luò)密切相關(guān).特別是很多實際網(wǎng)絡(luò)所抽象出來的復雜網(wǎng)絡(luò)，表現(xiàn)出了與以往網(wǎng)絡(luò)理論不同的特性［1］，如小世界特性、無尺度特性等.如何在復雜網(wǎng)絡(luò)環(huán)境下，保證網(wǎng)絡(luò)的可靠性和抗毀性［2］成為復雜網(wǎng)絡(luò)研究的重要課題.研究表明，在選擇性打擊下，即優(yōu)先攻擊網(wǎng)絡(luò)中“核心節(jié)點”，無標度網(wǎng)絡(luò)異常脆弱，網(wǎng)絡(luò)基本處于癱瘓狀態(tài).因此，找出網(wǎng)絡(luò)中的“核心節(jié)點”并將它們保護起來對維持整個網(wǎng)絡(luò)的可靠性具有重要作用;同時，“核心節(jié)點”的保障和維護對實現(xiàn)網(wǎng)絡(luò)信息流通和降低網(wǎng)絡(luò)信息交換成本，提高信息流通效率有重要意義.網(wǎng)絡(luò)節(jié)點的重要度指標的度量方法有節(jié)點的度、接近度、介數(shù)、信息、特征向量和累計提名等.其中最簡單的方法是以節(jié)點的度作為節(jié)點重要性的衡量標準，認為節(jié)點的度越大則該節(jié)點越重要，但一個節(jié)點的度僅僅描述了該節(jié)點對于其他節(jié)點的直接影響力，因此有很大的片面性;文獻［3］提出了一種基于生成樹數(shù)目的節(jié)點刪除法，如果多個節(jié)點的刪除都使得網(wǎng)絡(luò)不連通，那么這些節(jié)點的重要度將是一致的，從而使得評估不精確;文獻［4］提出的介數(shù)能很好地衡量節(jié)點重要度，但計算節(jié)點的介數(shù)非常復雜，不僅要計算各個節(jié)點對之間的最短路徑長度，還要記錄這些最短路徑的路線.

本文利用網(wǎng)絡(luò)的連通性來反映系統(tǒng)某種功能的完整性，通過度量節(jié)點刪除對網(wǎng)絡(luò)連通的破壞程度來反映網(wǎng)絡(luò)節(jié)點(集)的重要性，即“破壞性等價于重要性”.從這種思想出發(fā)構(gòu)造了一個和平均最短路徑指標具有等價性的節(jié)點重要度函數(shù)指標I(vi)，利用該函數(shù)可以有效地判定網(wǎng)絡(luò)中各節(jié)點重要程度的大小，并且無需復雜的計算，實例計算也驗證了該方法的合理性.

1 節(jié)點重要度評估模型

本文所研究的復雜網(wǎng)絡(luò)均為無向、無權(quán)、無重邊網(wǎng)絡(luò)，用圖G=(V，E)表示，其中V={v1，v2，…，vn}表示網(wǎng)絡(luò)G中節(jié)點的集合，E={e1，e2，…，em}為G中邊的集合.

定義1節(jié)點vi的度是指與它相關(guān)聯(lián)的邊的條數(shù)，記為ki.

定義2節(jié)點vi的鄰居節(jié)點是指與vi直接有邊相連的那些節(jié)點，這些節(jié)點的集合構(gòu)成vi的鄰居節(jié)點集.

定義3把vi和vj之間跳數(shù)最少的路徑稱為它們的最短路徑，顯然，vi和vj之間的最短路徑可能不止一條.

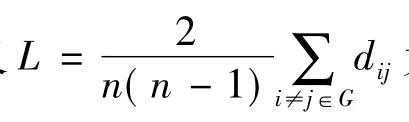
定義5定義li為刪除節(jié)點vi后，網(wǎng)絡(luò)中vi的鄰居節(jié)點集中保持連通的節(jié)點對數(shù)目.根據(jù)網(wǎng)絡(luò)中節(jié)點與邊的關(guān)系，有l(wèi)i為介于0與ki(ki-1)/2的正整數(shù).當li比較大時，表明刪除節(jié)點vi后，網(wǎng)絡(luò)的連通性仍然很好，即節(jié)點vi自身的重要性相對比較小，這個指標可以有效地反映節(jié)點的局部連通情況，因此可以用它來考慮網(wǎng)絡(luò)中節(jié)點的重要性.

定義6稱I(vi)=［ki(ki-1)］/［2(li+1)］為節(jié)點vi的重要度函數(shù)，考慮到葉子節(jié)點的li為0的情況，定義分母為li+1.該指標從節(jié)點自身的連接度和節(jié)點的局部連通性考慮了節(jié)點的重要性.同等條件下，連接度越大的節(jié)點收縮以后，網(wǎng)絡(luò)中節(jié)點和邊的數(shù)目就越少，因此該節(jié)點相對越重要.而處于關(guān)鍵位置的節(jié)點重要度也相對而言比較高，因為很多節(jié)點對之間的最短路徑都要經(jīng)過該節(jié)點，該節(jié)點收縮后將減少網(wǎng)絡(luò)的平均最短距離，因此該節(jié)點比較重要.

2 節(jié)點重要性指標

網(wǎng)絡(luò)節(jié)點之間進行通信的路徑首選最短路徑，如果某個節(jié)點被許多最短路徑經(jīng)過，則表明該節(jié)點在整個網(wǎng)絡(luò)中的作用和影響力是比較大的.因此，把網(wǎng)絡(luò)中平均最短路徑作為節(jié)點重要性指標是比較合理的，但是它的計算式比較復雜，因為不僅要計算出每個節(jié)點對之間的最短路徑長度，并且還要記錄這些最短路徑.下面分析說明本文定義的節(jié)點重要度函數(shù)指標與網(wǎng)絡(luò)中平均最短路徑指標具有一致性，只是放大的顯著性程度有所差別.

當節(jié)點vi被刪除或者收縮后網(wǎng)絡(luò)中平均最短路徑變化情況如下：

如果節(jié)點vi不在最短路徑上，則一部分節(jié)點的最短路徑不經(jīng)過vi.因此，當節(jié)點vi被刪除或者收縮后對這些節(jié)點的最短路徑無影響，從而對整個網(wǎng)絡(luò)的平均最短路徑也沒有影響.如果節(jié)點間的最短路徑經(jīng)過vi，則刪除節(jié)點vi后這些節(jié)點間的最短路徑將會發(fā)生變化.假設(shè)被刪除節(jié)點的li比較小，即節(jié)點vi的鄰居節(jié)點的連通性比較差，則最短路徑中經(jīng)過vi的鄰居節(jié)點的概率比較小.相對而言，經(jīng)過vi的最短路徑的概率就比較大，這與li減小，I(vi)增大是一致的.因此，節(jié)點的I(vi)越大，表明刪除節(jié)點vi后，通過vi的最大路徑變大，從而網(wǎng)絡(luò)的平均最短路徑變大.也就是，節(jié)點vi的I(vi)越大，刪除vi后網(wǎng)絡(luò)的平均最短距離變大.因此，本文定義的節(jié)點重要度函數(shù)指標與網(wǎng)絡(luò)中平均最短路徑指標具有一致性.

3 實例分析

設(shè)某網(wǎng)絡(luò)的拓撲結(jié)構(gòu)如圖1，用文獻［3］與文獻［5］得到節(jié)點4與節(jié)點6的重要度是一樣的，使用本文的方法有：節(jié)點4的度k4=4，l4為刪除節(jié)點4后，節(jié)點4的鄰居節(jié)點中保持連通的節(jié)點對數(shù)目，顯然l4=1，因此I(v4)=3.同樣很容易計算l(v6)=6.因此節(jié)點4的重要性程度比節(jié)點6要小.從直觀上也可以發(fā)現(xiàn)，當刪除節(jié)點4，節(jié)點1，2，3的連通性比刪除節(jié)點6后節(jié)點7，8，9的連通性要好，因此，節(jié)點4的重要性比節(jié)點6的重要性要小.

由表1知，本文使用節(jié)點重要度函數(shù)指標得到的節(jié)點重要度排序結(jié)果與文獻［7］中的方法得到的節(jié)點重要度排序結(jié)果是一致的，并且與實際結(jié)果是一致的.但是對于小型網(wǎng)絡(luò)，本文中計算節(jié)點重要度的方法更為簡單.此外，若通過文獻［3］的方法，即考慮刪除節(jié)點后網(wǎng)絡(luò)的生成樹變化數(shù)目的變化情況，則節(jié)點4～7的重要度是一樣的.然而從直觀上看，網(wǎng)絡(luò)中這幾個節(jié)點的重要度是有差別的.因此本文的方法是合理有效的.

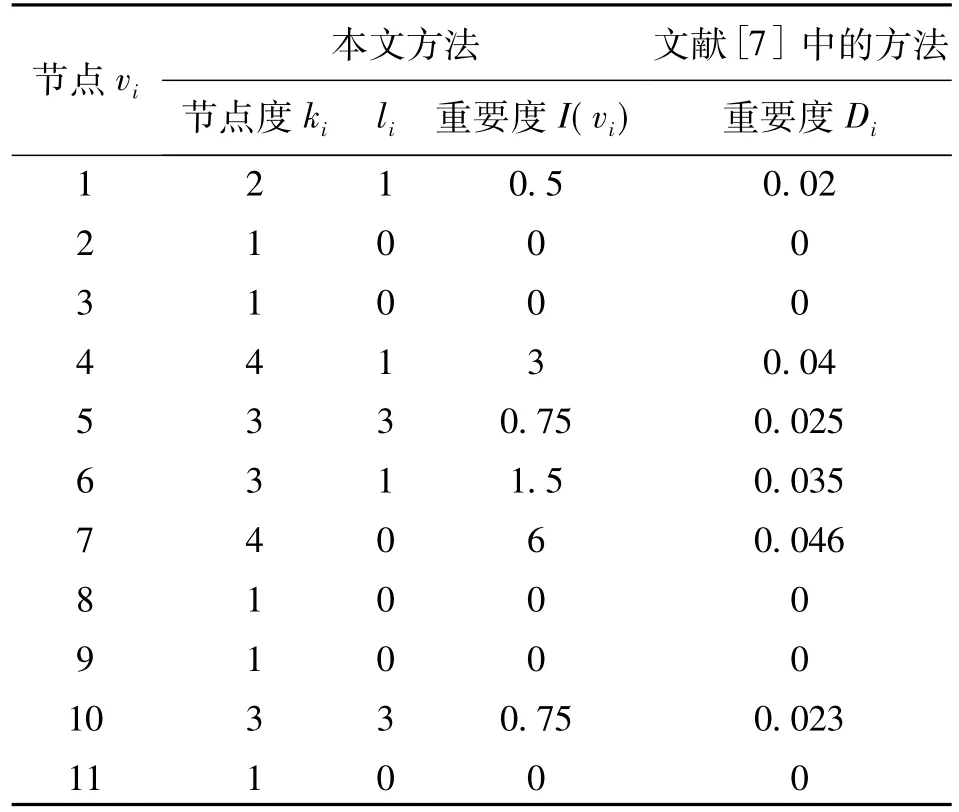
表1 節(jié)點重要度評估結(jié)果

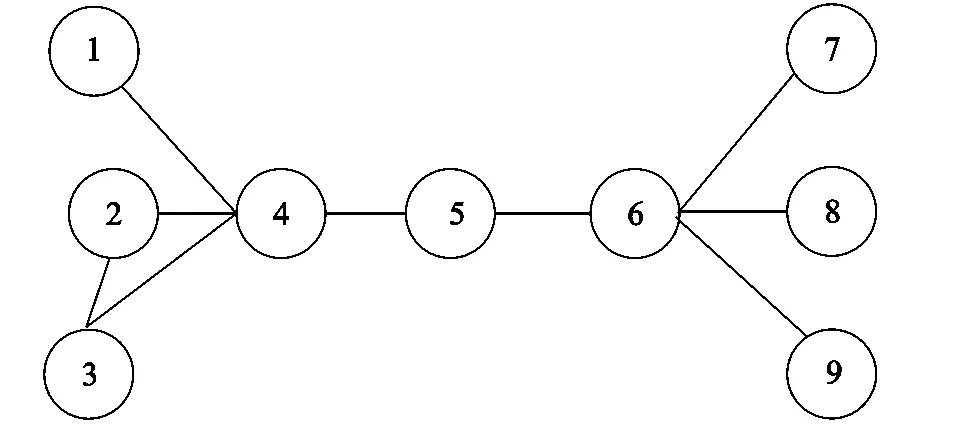
圖1 含有9個節(jié)點的網(wǎng)絡(luò)拓撲圖

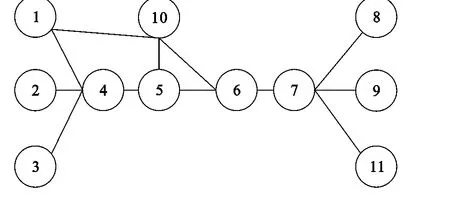
圖2 網(wǎng)絡(luò)拓撲結(jié)構(gòu)

4 結(jié)束語

評估網(wǎng)絡(luò)中的節(jié)點重要性一直是社會網(wǎng)絡(luò)分析領(lǐng)域和系統(tǒng)科學研究領(lǐng)域的一個熱點，本文基于“破壞性等價于重要性”這一思想，構(gòu)造了一個節(jié)點重要度函數(shù)，從而使這一思想得到了精細的量化.對于小型網(wǎng)絡(luò)，該方法避免了復雜的計算，實例分析也驗證了該方法的合理性、有效性和優(yōu)越性.

［1］汪小帆，李翔，陳光榮.復雜網(wǎng)絡(luò)理論及其應用［M］.北京：清華大學出版社，2006.

［2］饒育萍.林競焉，月東方.網(wǎng)絡(luò)抗毀度和節(jié)點重要性評價方法［J］.計算機工程，2009，35(6)：14-16.

［3］陳勇，胡愛群.通信網(wǎng)絡(luò)中最重要節(jié)點確定方法［J］.高技術(shù)通訊，2004(1)：573-575.

［4］FREEMAN L C.A set of measures of centrality based upon betweenness［J］.Sociometry，1977，40(1)：35-41.

［5］譚躍進，吳俊，鄧宏鐘.復雜網(wǎng)絡(luò)中節(jié)點重要度評估的節(jié)點收縮方法［J］.系統(tǒng)工程理論與實踐，2006，26(11)：78-83.

［6］陳勇，胡愛群，胡嘯.通信網(wǎng)中節(jié)點重要性的評價方法［J］.通信學報，2004，25(8)：129-134.

［7］陳靜，孫林夫.復雜網(wǎng)絡(luò)中節(jié)點重要度評估［J］.西南交通大學學報，2009，44(3)：426-429.

［8］孫睿，羅萬伯.網(wǎng)絡(luò)輿論中節(jié)點重要性評估方案綜述［J］.計算機應用研究，2012，29(10)：3 606-3 608.

［8］葉春森，汪傳雷，劉宏偉.節(jié)點重要度評價方法研究［J］.統(tǒng)計與決策，2010(1)：22-24.

［9］李鵬翔，任玉晴，席酉民.網(wǎng)絡(luò)節(jié)點(集)重要性的一種度量指標［J］.系統(tǒng)工程，2004，22(4)：13-20.

An evaluation index of node importance in complex networks

JIANG Feng-jing，CHEN Yue-qi

(College of Science，Xidian University，Xi'an 710071，China)

To simply and effectively evaluate the importance of each node in network topology structure，a node importance function based on the node connectivity degree and local connectivity is defined.The index of the node importance function is substantially consistent with the index of the average shortest path in networks，the importance of each node in the network can be sorted by the size of the index value.For small networks，it is relatively simple in calculation，the method is vertified more intuitive，effective and reasonable by theoretical analysis and practical examples.

node importance;neighbor node;node removal;average shortest distance

C 934

A

1674-649X(2014)01-0140-03

編輯：：武暉;校對：孟超

2013-04-15

蔣豐景(1989-)，男，江蘇省淮安市人，西安電子科技大學碩士研究生.E-mail：727729909@qq.com