實值信息系統上基于熵的屬性約簡

魯文霞，馬盈倉

(西安工程大學理學院，陜西西安710048)

實值信息系統上基于熵的屬性約簡

魯文霞，馬盈倉

(西安工程大學理學院，陜西西安710048)

研究實值系統中的知識獲取是粒計算研究的主要方向之一.為給出一種高效的知識獲取方法，文中基于鄰域粗糙集的原理，針對實值特點，在實值信息系統上給出熵和基于熵的屬性重要度的定義和約簡定理.同時研究其性質，并給出了實值信息系統上基于熵的屬性重要度的約簡算法，對算法的性質進行了分析，通過實例驗證了該算法的有效性.

粗糙集理論;實值系統;屬性約簡;熵

0 引言

粗糙集作為一種處理不協調、不確定與不完備數據的新的數學理論［1-2］，最初是由波蘭科學家Pawlak于1982年提出的.近幾年來，它已經成功地應用于機器學習、模式識別、決策支持、數據挖掘、過程控制等領域［3-5］.

然而經典粗糙集理論是基于等價關系的，分類過于苛刻，它適用于處理離散型變量，對于現實中廣泛存在的數值型數據卻不能直接處理.在金融、醫療、科研和工程領域，實值型變量無處不在，如：配電系統診斷的電流信號［6］等.為了解決這種問題，人們在經典粗糙集的基礎上進行了許多有意義的推廣，引入了很多新的模型，如模糊粗糙集模型［7-10］、鄰域系統粗糙集模型［11］和鄰域關系模型［12］.其中，在鄰域模型方面，Hu提出基于鄰域粒化和粗糙逼近的數值屬性約簡［12］，Yao［13］提出1-step鄰域，Wu［14］提出并研究了k-step鄰域信息系統的性質，以及帶有誤差范圍和測試代價的數據屬性約簡［15］等.可以看出，不同的模型是基于不同的粒化和逼近機制來處理現實中實值型數據.

粗糙集理論中的約簡一直是核心問題.合理的屬性約簡可以起到非常有效的作用，對于知識獲取、決策分析等起到指導作用.一般地講，一個決策系統的屬性約簡往往不是惟一的，理想中人們期望找到決策系統中的最小約簡，但是找到最小約簡是一個NP-hard的問題，所以在現實生活中人們解決這一類問題一般采取啟發式算法來求出最優或次最優約簡.在經典粗糙集模型上，借助熵及條件熵作為度量可以對屬性進行約簡［16］.在實值系統上也有人在這方面作了文章，如：協調覆蓋決策系統下基于條件信息熵的屬性約簡［17］，覆蓋決策信息系統的約簡［18］，模糊概率近似空間及其信息度量［19］等.本文在經典粗糙集熵的定義和鄰域粗糙集模型研究的基礎上，提出了實值信息系統上的熵和基于熵的屬性重要度的定義，它是等價關系上一個推廣，并研究了其性質.在實值信息系統上，給出了在熵定義下的約簡定理，提出了基于熵的屬性重要度約簡算法，同時對算法的性質進行了理論分析，揭示了屬性重要度作為啟發式算法的合理性;最后通過實例，表明該算法是有效的.

1 鄰域覆蓋粗糙集

定義1［11］給定一個n維的實數空間Ω，ΔRN×RN→R，稱Δ是RN上的一個度量，如果Δ滿足：

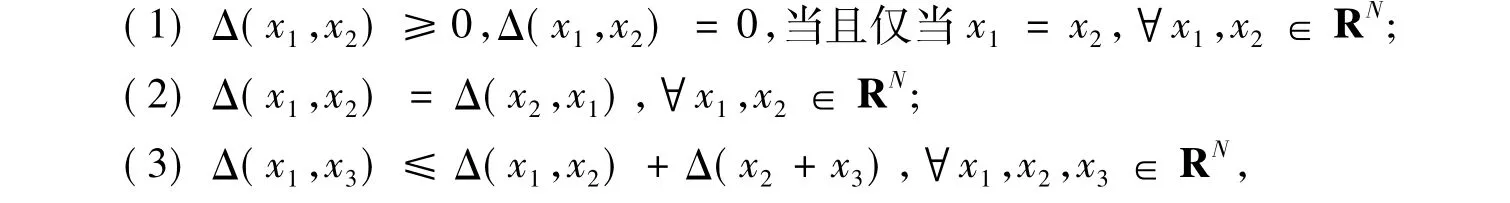
則稱〈Ω，Δ〉為度量空間.歐式距離是實數空間上常用的度量.

定義2實值信息系統S=(U，A)，xi∈U，a∈A，xi的關于屬性a的e-鄰域為

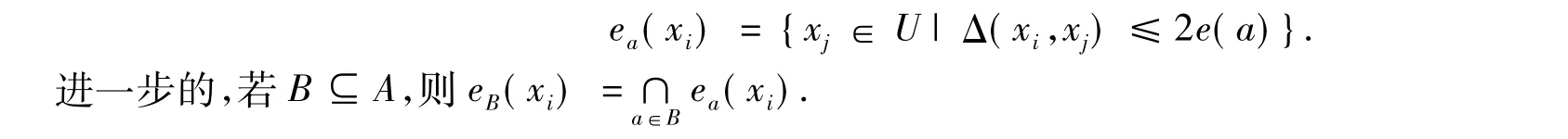
注e(a)為誤差范圍.

根據度量的性質，有如下結論：

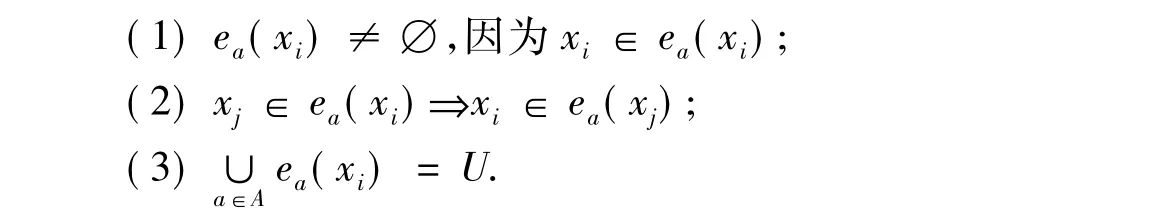
不難看出，鄰域粒子族{ea(xi)|i=1，2，…，n}構成了U的一個覆蓋.

進一步的，由鄰域的定義，可以得到

性質1(1)eB1∪B2=eB1∩eB2，(2)?xi∈U，e1≤e2，則e1(xi)?e2(xi).

2 實值信息系統中基于熵的約簡

2.1 鄰域下的熵

定義3實值信息系統S=(U，A)，xi∈U，B?A，則屬性集B具有的信息熵定義為

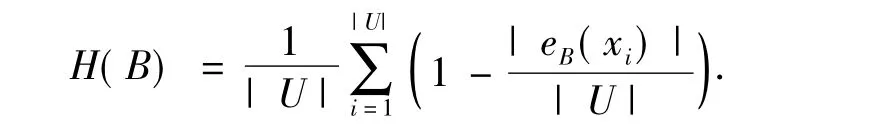
其中|U|表示論域中元素的個數，|eB(xi)|/|U|表示xi的B鄰域在U中的概率.

注此定義是經典粗糙集中熵的一種推廣，可以退化為等價關系中定義的熵.

定理1實值信息系統S=(U，A)，xi∈U，B?A，則H(B)≤H(A).

證明由于

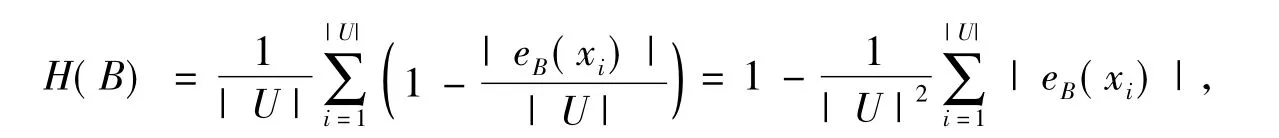
由鄰域的定義B?A，則

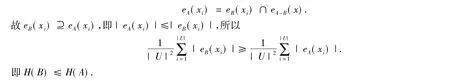
2.2 鄰域下的屬性重要性的度量

定義4實值信息系統S=(U，A)，xi∈U，a∈A，屬性a在A中的重要性定義為

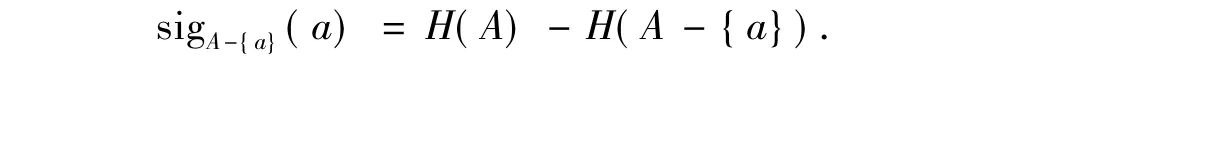
特別當A={a}時，用sig(a)表示sig?(a)：

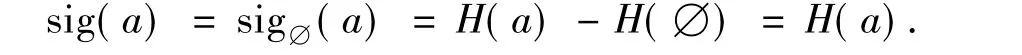
定義5實值信息系統S=(U，A)，a∈A，若H(A)≠H(A-{a})，則稱屬性a在A中是必要的，否則就是不必要的.

性質2(1)0≤sigA-{a}(a)≤1;(2)屬性a∈A在A中是必要的充要條件是sigA-{a}(a)＞0;(3) CORE(A)={a∈A|sigA-{a}(a)＞0}.

證明(1)由定理1的結論可知，0≤sigA-{a}(a)≤1.

(2)充分性：若a∈A在A中是必要的，則H(A)≠H(A-{a}).而H(A)≥H(A-{a})，故sigA-{a}(a)＞0.

必要性：若sigA-{a}(a)＞0，即H(A)≠H(A-{a})，故a∈A在A中是必要的.

(3)由性質(2)可知.

定義6實值信息系統S=(U，A)，xi∈U，B?A，任意屬性a∈A-B關于屬性集B中的重要性定義為

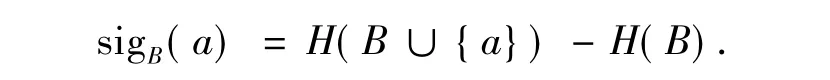
通過信息系統屬性約簡的概念和以上結論，可以容易地得到如下定理，它通過熵來刻畫信息系統約簡.

定理2實值信息系統S=(U，A)，B?A，如果：(1)H(A)=H(B)，(2)?a∈B，有sigB-{a}(a)＞0，則B為A的一個約簡.

證明在實值信息系統中B?A為A的一個約簡的充分必要條件為eA(xi)=eB(xi)且B是獨立的.

由定理1知，當B?A時，eA(xi)=eB(xi)成立的充分必要條件是H(A)=H(B).B是獨立的成立的充分必要條件是?a∈B是必要的，則H(B)≠H(B-{a})，即sigB-{a}(a)＞0.故定理成立.

2.3 屬性重要性的約簡算法

由于核屬性是所有約簡的交集，因此，在求最小約簡時可以把核作為起點，在性質2中可以很容易地求出屬性集的核.再根據定義4中定義的屬性重要度作為啟發式函數，選擇重要度最大的屬性添加到核中去，直到熵等于整個條件屬性的熵為止.

實值信息系統的核與約簡算法：

輸入：實值信息系統S=(U，A)，其中U為論域，A為條件屬性.

輸出：該信息系統的核和約簡.

步驟1求CORE(A)，計算每個屬性a∈A在A中是否必要，且令CORE(A)=?.若sigA-{a}(a)＞0，則CORE(A)：=CORE(A)∪{a}，最后得到的CORE(A)為屬性集A的核;若H(A)=H(CORE(A))則終止(此時CORE(A)為A的最小約簡);否則，執行步驟2.

步驟2令C=CORE(A)，對屬性集A-C重復執行：當C=?時，計算每一個屬性a∈A的熵H({a})，若H({a})=H(A)，則終止(此時{a}為A的最小約簡);當C≠?時，轉以下步驟：

(1)對每個屬性a∈A-C，計算sigC(a).

(3)若H(C)=H(A)，則終止(此時C為A的最小約簡);否則，轉(1).

以上是依據熵的屬性重要度求屬性約簡的算法步驟，該算法是有效的，下面通過例子進行分析.

例1實值信息系統S=(U，A)，如表1，其中U={x1，x2，x3，x4，x5}，A={a1，a2，a3}，求其信息表的核與約簡.其中，Δ(x1，x2)=|a(xi)-a(xj)|.

步驟1由于

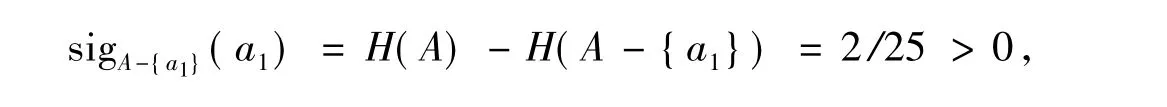
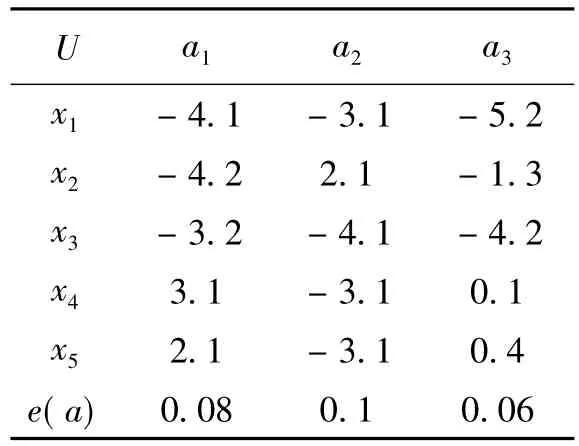
表1 信息表

故A中必要元素為a1，即CORE(A)={a1}.

步驟2令C={a}，對屬性a2，a3∈A-C，計算sigC(a2)，sigC(a3).

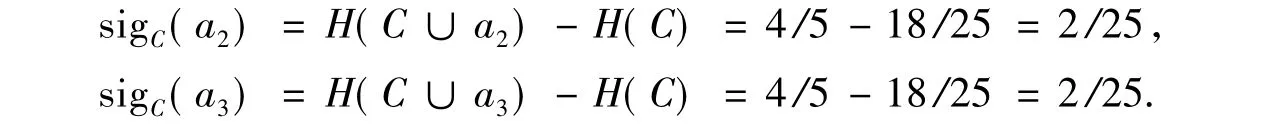
若選擇屬性a2，C：=C∪{a2}，則H(C)=H(A)，終止.

若選擇屬性a3，C：=C∪{a3}，則H(C)=H(A)，終止.

所給算法求出信息系統的核CORE(A)={a1};約簡為{a1，a2}或{a1，a3}.

3 結束語

本文在鄰域覆蓋粗糙集的定義下，將經典粗糙集中的熵和屬性重要度推廣到實值信息系統中，給出了其在實值系統上的定義，并給出了實值信息系統在熵下的約簡定理.在此基礎上，提出了一種基于熵的屬性重要度的實值信息系統上的屬性約簡算法，并通過例子驗證了該算法的有效性.今后將對實值決策系統在條件熵上的屬性約簡進行研究，并將其應用到UCI數據中，與其他算法進行比較.

［1］PAWLAK Zdzislaw.Rough sets［J］.International Journal of Computer and Information Sciences，1982，11(5)：341-356.

［2］張文修，吳偉志，梁吉業，等.粗糙集理論與方法［M］.北京：科學出版社，2005：1-15.

［3］朱永利，吳立增，李雪玉.貝葉斯分類器與粗糙集相結合的變壓器綜合故障［J］.中國電機工程學報，2005，25(10)：159-165.

［4］孫秋野，張化光.基于粗糙集的配電系統連續信號故障診斷方法［J］.中國電機工程學報，2006，26(11)：156-161.

［5］劉清，劉少輝，鄭非.Rough邏輯及其在數據約簡中的應用［J］.軟件學報，2001，12(3)：415-419.

［6］SNN Q Y，ZHANG H G.Fault diagnose algorithm of distribution system by continuous signals based on rough sets［J］.The Chinese Society for Electrical Engineering，2006，26(11)：156-161.

［7］羅承忠.模糊集引論［M］.北京：北京師范大學出版社，2007：45-48.

［8］高新波.模糊聚類分析及其應用［M］.西安：西安電子科技大學出版社，2004：44-45.

［9］SLAVKA B.Approximation of fuzzy concepts in decision making［J］.Fuzzy Sets and Systems，1997，85(2)：23-29.

［10］RADZIKOWSKA M，KERRE E E.Comparative study of fuzzy rough sets［J］.Fuzzy Sets and System，2002，126(2)：29-34.

［11］HU Qinghua，ZHANG Lei，CHEN Degang.Gaussian kernel based fuzzy rough sets：Model，measures and applications［J］.International Journal of Approximate Reasoning，2010，51(1)：453-471.

［12］胡清華，于達仁，謝宗霞.基于鄰域粒化和粗糙逼近的數值屬性約簡［J］.軟件學報，2008，19(3)：640-649.

［13］YAO Y.Y.Relational interpretation of neighborhood operators and rough set approximation operators［J］.Information Science，1998，111(1)：239-259.

［14］WU Weizhi，ZHANG Wenxiu.Neighborhood operator systems and approximations［J］.Information Science，2002，144(1-4)： 201-217.

［15］MIN Fan，ZHU William.Attribute reduction of data with error ranges and test costs［J］.Information Science，2012，18(4)：3-14.

［16］張海軍，梁吉業，梁春華.一種基于知識量的約簡算法［J］.小型微型計算機系統，2007，28(11)：1968-1971.

［17］夏秀云，秦克云，田浩.協調覆蓋決策系統下基于條件信息熵的屬性約簡［J］.河南大學學報：自然科學版，2010，40 (4)：406-410.

［18］許晴媛，李進金，張燕蘭.覆蓋決策信息系統的約簡［J］.山東大學學報：理學版，2010，45(1)：89-93.

［19］HU Qinghua，YU Daren，XIE Zongxia，et al.Fuzzy probabilistic approximation spaces and their information measures［J］.IEEE Transactions on Fuzzy Systems，2006，14(2)：191-201.

Attribute reduction of the real value information system based on entropy

LU Wen-xia，MA Ying-cang

(School of Science，Xi'an Polytechnic University，Xi'an 710048，China)

Research knowledge acquisition of the real value system is one of the main directions of the granular computing research.For giving an efficient knowledge acquisition method，based on the neighborhood of rough set theory and according to the characteristics of the real value，the definition of the entropy and attribute importance based on the entropy and reduction theorem in the real value information system are given，and its properties are studied.Moreover，the algorithm of attribute reduction based on attribute importance in the real value information system is proposed.Lastly，the properties of algorithm are discussed and the effectiveness of the algorithm are showed by an example.

rough set theory;real system;attribute reduction;entropy

TP 18;B 815

A

1674-649X(2014)01-0128-05

編輯、校對：武暉

2013-07-04

國家自然科學基金資助項目(61170128);陜西省教育廳專項科研計劃項目(12JK0878);西安工程大學研究生創新基金資助(chx131114)

馬盈倉(1972-)，男，陜西省合陽縣人，西安工程大學教授，博士，主要研究領域為粗糙集理論及應用、非經典數理邏輯.E-mail：mayingcang@126.com