相空間混沌擴頻通信及其誤碼率

吳成茂，李杜娟

（西安郵電大學 電子工程學院，陜西 西安710121）

隨著通信技術的快速發展，擴頻通信現已具有較強的抗干擾、抗噪聲、抗多徑衰落等性能特性，在軍事通信中不僅發揮出了不可替代的作用，同時在民用和商用通信的各個方面也有了廣泛地滲透，如衛星通信、移動通信、微波通信、全球個人通信、蜂窩系統、無線定位系統、無線局域網等［1］。擴頻通信，其傳輸速率不僅較高，而且其傳輸的可靠性和安全性能也得到了較大改善。近年來，在擴頻通信理論研究中，信號調制方式［2］、擴頻增益［3］、干擾方式［4］，以及信噪比［1］等對擴頻通 信誤碼率的影響，已被學者們進行了探討，并將采用誤碼率作為衡量擴頻系統性能指標的重要依據，以此來解決信道干擾、多徑信號引起的衰落，以及通信安全等重要問題。但是擴頻通信系統還尚有一些不足，由于信號之間非正交性且相似，易與其他設備間產生相互干擾，使得通信系統通信效率降低且傳輸的可靠性變差，以致通信系統質量受到影響。為了解決擴頻通信中存在的以上問題，文獻［5－7］提出了采用混沌映射產生擴頻碼實現直擴通信，但不同類型的混沌信號所產生混沌序列［8］性能具有較為明顯的差異。因此，尋找適合擴頻通信的混沌信號成為當前混沌通信中的熱點問題，也正是本文所要探究的問題所在。通過測試經典Logistic映射所產生混沌序列和相空間混沌序列作為擴頻碼應用于擴頻通信系統的誤碼率，對比分析誤碼率與相應序列間的統計相關特性，并揭示二者之間的關聯性，為擴頻通信系統尋找較低誤碼率的擴頻碼產生方式。

1 相空間混沌擴頻通信系統

為了使得擴頻通信系統的通信質量有所提高，擬將在擴頻通信系統中引入不同相空間混沌信號，其中相空間混沌擴頻通信的原理如圖1所示。

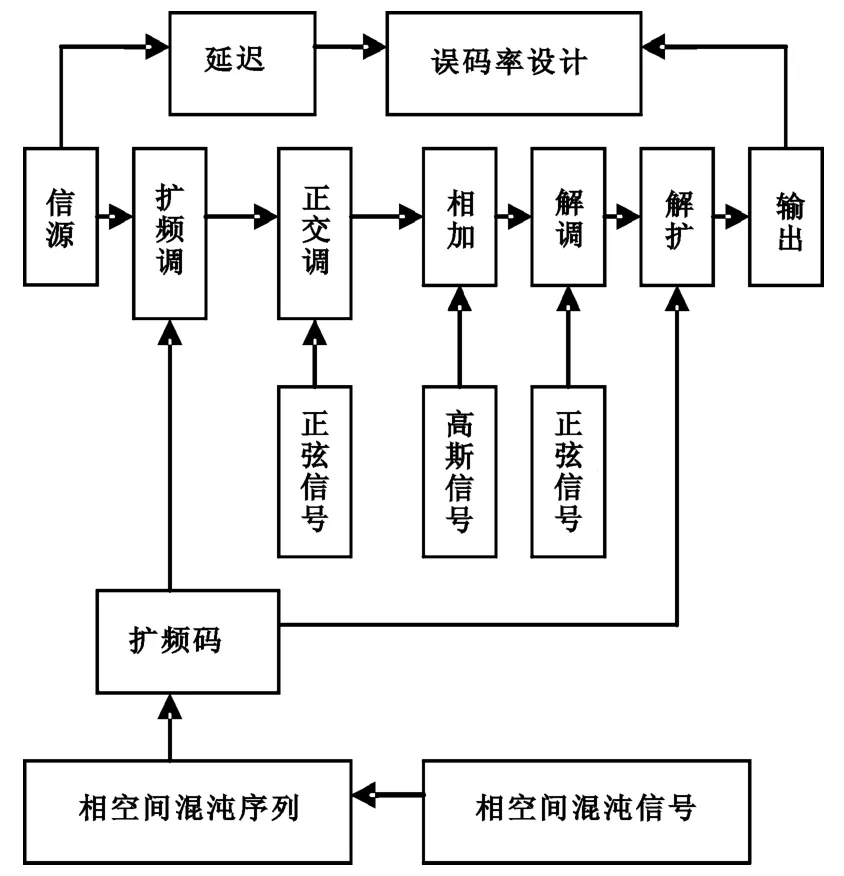
圖1 相空間混沌擴頻通信系統

2 混沌序列的產生方式

擴頻碼作為擴頻通信的關鍵，其產生方式不同，使得擴頻通信系統的性能將會有所差異。經典Logistic映射及其利用相空間法改良混沌序列產生擴頻碼的基本原理如下。

2.1 Logistic映射

Logistic映射具有良好的混沌特性，在混沌保密通信的很多領域都被廣泛應用。Logistic映射表達式為［9］

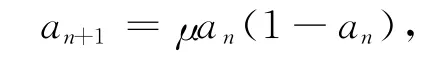
其中μ為控制參數，a1為初始條件。若該映射的控制參數滿足

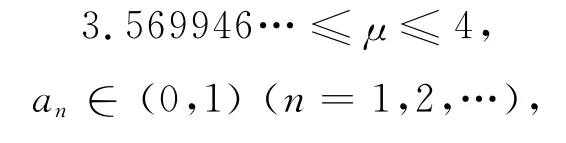
則Logistic映射處于混沌狀態。當μ＝4時，Logistic映射為滿射。

2.2 相空間混沌信號

混沌信號具有良好的初值敏感性和相關特性等性能，近年來被作為擴頻序列產生研究的重要方法。

文獻 ［10］提出了 Autocorrelation of Phasespace Axial Symmetric（APAS）定理，對于一個平穩遍歷的離散實動力系統

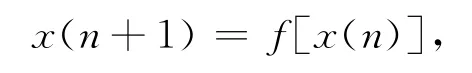
其值域為［－a，a］，a為正實數；｛x（n）｝的均值為0，且取值的正負具有統計平衡性。

相空間混沌信號分為低維混沌信號、高維混沌信號和空時混沌信號3種。

（1）低維混沌信號

在低維混沌信號中，以改良Henon序列為例來對其特性作說明，其動力方程為［10］

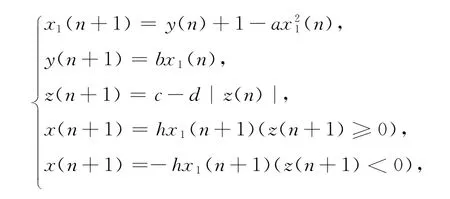
其中x（n）∈ ? 是狀態變量；a，b，c，d，h是系統參數，且為正數。

（2）高維混沌信號

在高維混沌信號中，其序列在多個方向上都具有擴張性。選取CML序列作對稱性改良，其動力方程為［10］

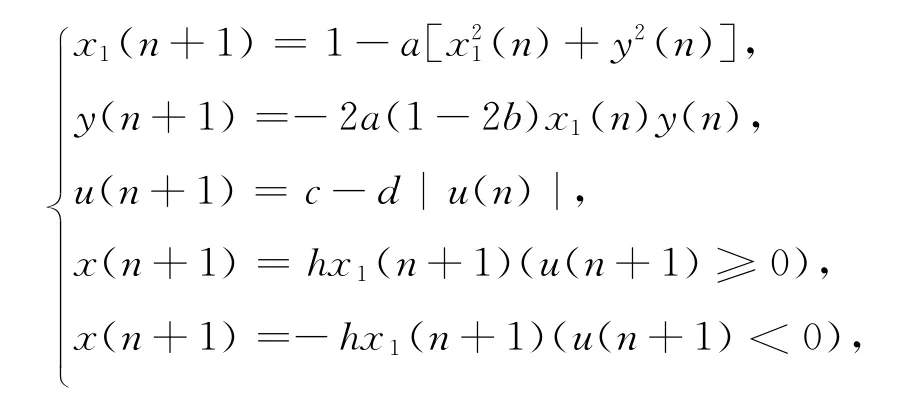
其中x（n）∈ ? 是狀態變量；a，b，c，d，h是系統參數，且為正數。

（3）空時混沌信號

所謂空時混沌系統，就是序列在空間和時間上的演化都有耦合性，并且該行為表現出了極大的復雜性，現如今已有了廣泛應用。因此，利用空時混沌系統來改良基于Logistic映射的OCML序列，其動力方程為［10］

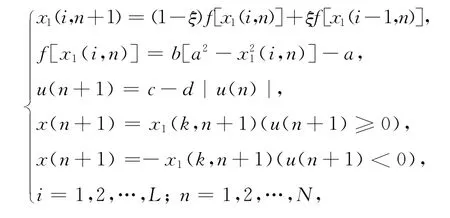
其中x（i，n）∈ ? 是狀態變量；f（x）是Logistic映射；a，b，c，d，ξ，k是系統參數；L 是空時系統的尺度；N是序列的長度。

3 混沌序列性能分析

混沌序列性能指標是衡量混沌信號性能好壞的重要指標，對擴頻通信系統的性能有著重要影響。因此，對以下混沌信號的指標性能進行測試分析。

3.1 李雅普諾夫指數

n維系統的Lyapunov指數定義式為［10］

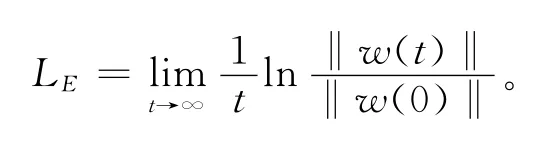
在Matlab下，對經典Logistic映射及其利用相空間法改良后混沌序列的Lyapunov指數進行仿真測試，所得結果分別如圖2和圖3所示。

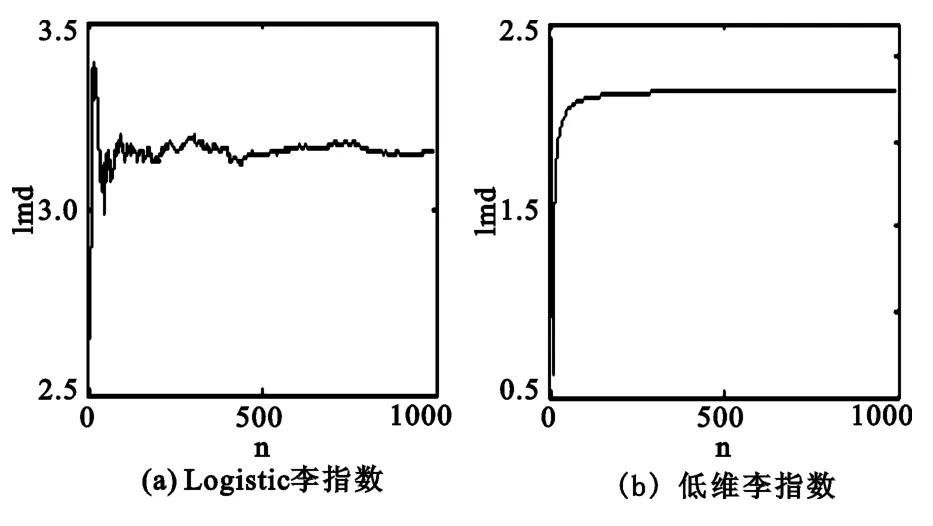
圖2 Logistic和低維混沌序列Lyapunov指數

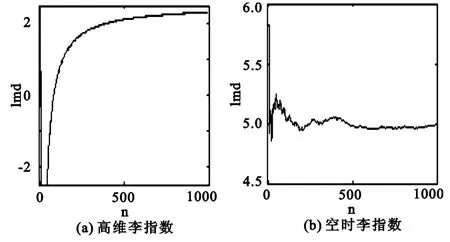
圖3 高維和空時混沌序列Lyapunov指數

將上述不同擴頻序列的最大Lyapunov指數測試結果進行比較，詳細結果如表1所示。

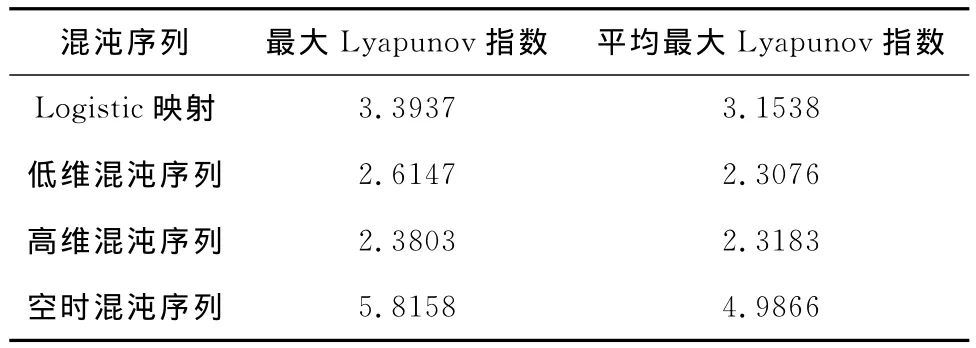
表1 最大Lyapunov指數仿真測試結果

3.2 相關性

對于擴頻序列，設｛ai｝與｛bi｝是周期為N的兩個碼序列，即

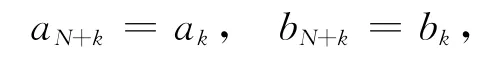
碼字｛ai｝與｛bi｝的互相關函數Rab（τ）定義為［11］

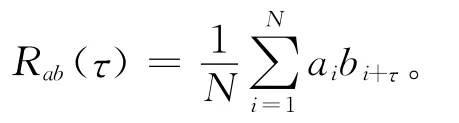
若Rab（τ）＝0，則｛ai｝與｛bi｝正交。

長度為N的碼序列｛ai｝的自相關函數Ra（τ）定義為［11］

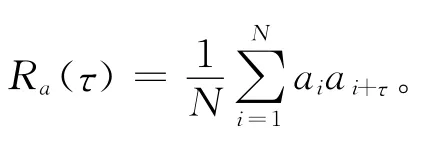
在Matlab下，對經典Logistic映射及其利用相空間法改良后混沌序列的相關特性進行仿真測試，所得結果分別如圖4至圖7所示。

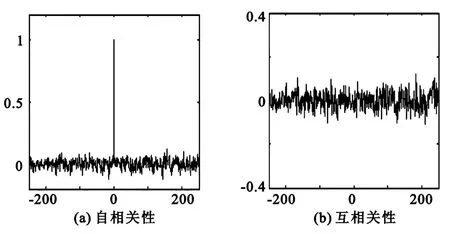
圖4 Logistic混沌序列相關性

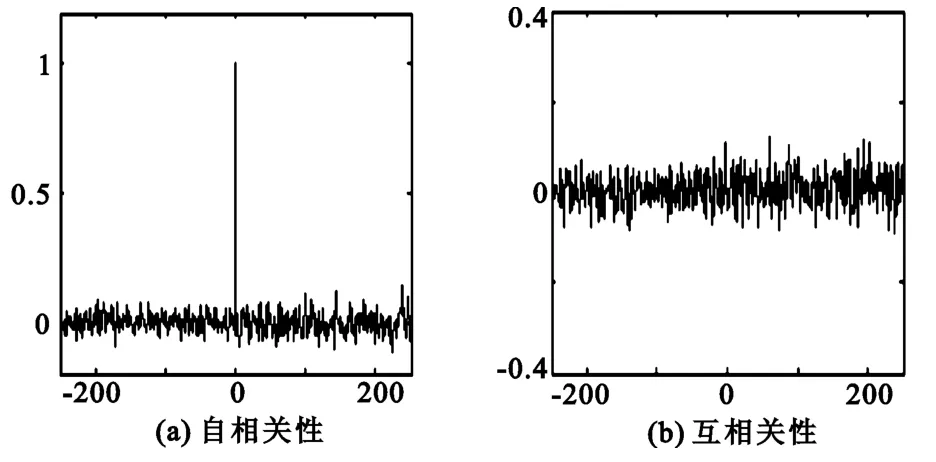
圖5 低維混沌序列相關性

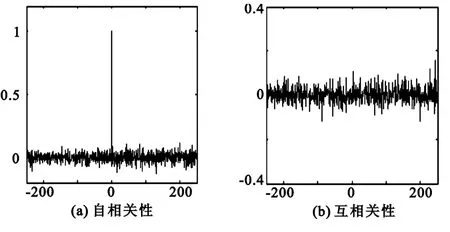
圖6 高維混沌序列相關性

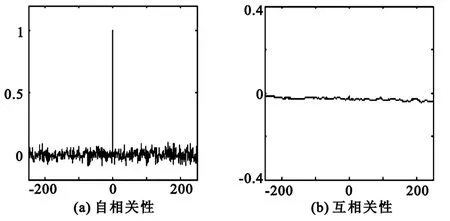
圖7 空時混沌序列相關性

將上述不同類型混沌序列的相關性曲線測試結果進行比較和分析，其詳細結果如表2所示。

表2 不同混沌序列的相關性比較

3.3 均值和方差

概率論中，均值和方差是用來描述隨機變量分布特點的兩種最常用的數字特征。

均值反映了隨機變量平均取值的大小，其定義式為［12］

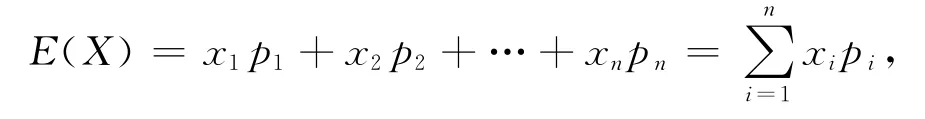
其中E（X）是均值，pi為不同情況下的隨機變量X對應的概率。

方差是用來度量隨機變量和均值之間的偏離程度，其計算公式定義為

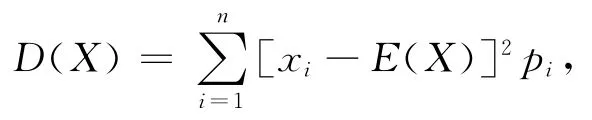
其中D（X）為方差，E（X）和pi分別為隨機變量X對應的均值和X＝xi的概率。

為了對混沌序列的互相關性作進一步的定量分析，在仿真測試經典Logistic映射和利用相空間法改良混沌信號所產生的混沌序列互相關特性時，對其描述互相關特性曲線特征的均值和方差也進行了測試，其測試結果如表3所示。

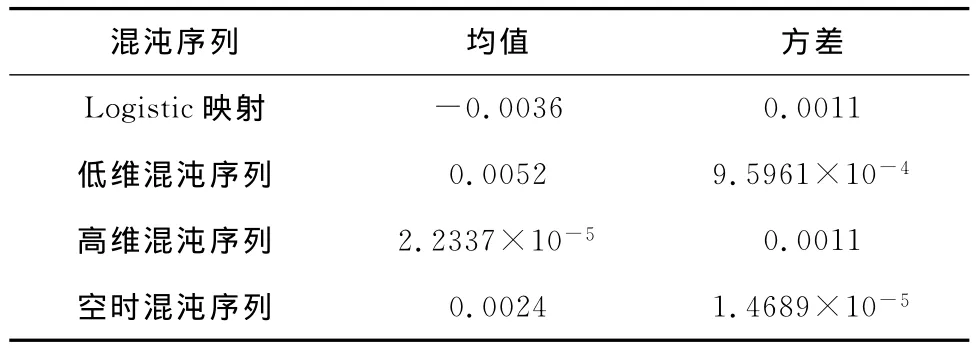
表3 混沌序列互相關性曲線的均值和方差

4 擴頻系統的誤碼率

將不同混沌序列作為擴頻碼應用于擴頻通信系統中，并對其誤碼率進行測試。

4.1 擴頻通信系統的誤碼率

誤碼率作為衡量通信系統可靠性的一個重要指標，其計算方法依據柯捷爾尼科夫理論可知，擴頻通信系統誤碼率的表達式為

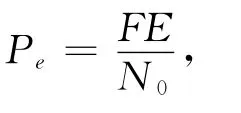
其中F為信號的頻率，E為信號能量；N0為噪聲功率譜密度。而在實際的相空間混沌擴頻通信中，其誤碼率的計算可采用

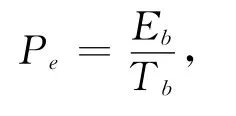
其中信號傳輸中出現錯誤的比特數為Eb，總的傳輸信號的比特數為Tb。

在實驗仿真測試中，所采用的測試條件和測試方法參照文［13］所述，此處不再贅述。

4.2 相空間擴頻碼誤碼率測試分析

在混沌擴頻通信中，將不同混沌序列作為擴頻碼應用于擴頻通信系統中，其誤碼率結果如表4所示。

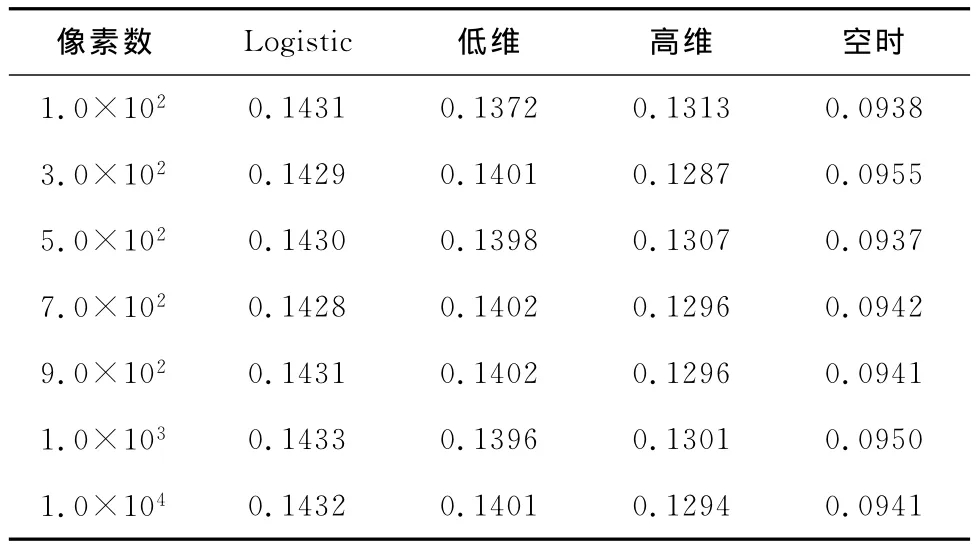
表4 不同混沌序列在不同像素下的誤碼率

由表4可知，經典Logistic映射所產生混沌序列的誤碼率平均值約為0.143；利用相空間法改良混沌序列，采用低維混沌序列作為擴頻碼的誤碼率平均值約為0.139，采用高維混沌序列作為擴頻碼的誤碼率平均值約為0.130，采用空時混沌序列作為擴頻碼的誤碼率平均值約為0.094。表明Logistic混沌序列誤碼率性能相對最差，改良后的空時混沌序列的誤碼率性能相對最好。其原因在于改良后的空時混沌序列的自相關性和互相關性相比都非常好，而經典Logistic映射產生混沌序列的自相關性和互相關性都是較好，相比其他相空間混沌序列的相關特性較差（見表2）。相比而言，利用相空間法改良低維混沌序列比經典Logistic映射產生混沌序列的誤碼率降低了0.004，高維混沌序列比經典Logistic混沌序列的誤碼率降低了0.013，空時混沌序列比經典Logistic混沌序列的誤碼率降低了0.049。顯然，空時混沌序列的誤碼率相對減少的最多，其值為4.9%。原因在于利用相空間法改良后的空時混沌序列所對應的自相關和互相關特性都相比最好，因此，所對應的誤碼率更低是合理的，保證了信號傳輸的準確率，有利于擴頻通信系統的需要。

通過將表2中的擴頻碼序列的統計相關特性與表4中所對應的誤碼率作對照，結果發現擴頻碼序列的統計相關特性與其相應誤碼率的大小之間存在很大的關聯性。相比統計互相關特性，擴頻碼的統計自相關特性對擴頻系統誤碼率的影響頗為明顯。而對于統計自相關特性相同的兩個擴頻序列，其統計互相關特性相對較好的擴頻序列所對應的誤碼率將會更低。

5 結論

通過仿真實驗，對經典Logistic映射所產生混沌序列和利用相空間法改良后混沌序列作為擴頻碼的誤碼率進行了測試，結果表明擴頻碼的誤碼率大小與其相應的統計相關特性之間有密切聯系。實驗發現，利用相空間法改良后的空時混沌序列作擴頻碼，能夠相對較好的降低擴頻系統的誤碼率，保證信號傳輸的準確率，提高了擴頻系統的安全性，有利于擴頻通信需要。

［1］黃乘順，李星亮.基于混沌的擴頻通信系統及性能分析［J］.通信技術，2008，41（12）：37－39.

［2］張蕾，鄭實勤.基于MATLAB的直接序列擴頻通信系統性能仿真分析研究［J］.電氣傳動自動化，2007，29（3）：39－42.

［3］王亥，胡健東.數字混沌擴頻通信系統［J］.北京郵電大學學報，1998，21（4）：7－11.

［4］曾璐，謝曉堯.基于MATLAB擴頻通信系統誤碼率的研究［J］.通信技術，2011，44（11）：25－29.

［5］張怡，費恒敏，趙恒斌，等.混沌序列相關特性研究及在擴頻通信中的應用［J］.火力與指揮控制，2011，36（11）：18－24.

［6］劉利，張建東，鄭志軍.混沌擴頻通信系統仿真［J］.艦船電子工程，2010，196（10）：75－103.

［7］田東，何世彪，鄭鵬宇.基于數字混沌編碼器的擴頻通信研究［J］.數字通信，2012，7（1）：29－36.

［8］劉雪松，李立萍.混沌擴頻通信系統及其干擾技術研究［D］.成都：電子科技大學，2009：22－24.

［9］范九倫，張雪峰.分段Logistic混沌映射及其性能分析［J］.電子學報，2009，29（7）：720－725.

［10］陳濱，周正歐.混沌波形的相關性［M］.西安：西安電子科技大學出版社，2011：13－136.

［11］田日才.擴頻通信［M］.北京：清華大學出版社，2007：61－62.

［12］盛驟，謝式千，潘承毅.概率論與數理統計［M］.3版.北京：高等教育出版社，2001，68－156.

［13］吳成茂，李杜娟，王保平.混沌擴頻通信及其誤碼率［J］.西安郵電大學學報，2013，18（3）：10－13.