數學：連接有限與無限的金橋
——讀趙煥光教授等《夢想相遇無窮》有感

季理真，章勤瓊（譯）

（1．密歇根大學，美國 密歇根 48109；2．溫州大學，浙江 溫州 325035；3．南京師范大學，江蘇 南京 210023）

數學：連接有限與無限的金橋
——讀趙煥光教授等《夢想相遇無窮》有感

季理真1，章勤瓊（譯）2，3

（1．密歇根大學，美國 密歇根 48109；2．溫州大學，浙江 溫州 325035；3．南京師范大學，江蘇 南京 210023）

在數學中，無窮的概念非常重要，處于中心地位．從著作《夢想相遇無窮》出發，討論無窮以及與之相關的幾個概念，如完備、緊致、退化等，進而探討當代數學中由這些概念導出的主要理論與定理．

無窮；極限；完備；緊致；退化

與初等數學以常量為研究對象，以靜止觀點研究問題不同，高等數學的研究對象主要為變量，讓運動和辯證法進入了數學．微積分是高等數學的基礎課程，也是學習許多其它課程的重要工具．微積分以函數為研究對象，通過連續這一橋梁，利用極限為主要方法進行研究．由于微積分有關概念的相對抽象性，不少學生在初學時感到枯燥與困難．因此，為了有助于學生更容易理解微積分相關概念，產生進一步學習與探索的興趣與欲望，有必要從數學、哲學、歷史、人文等更寬廣的視野出發，對微積分中的一些重要概念做出闡釋．

1 無 窮

自人類文明開始以來，人們就已經開始思考并探索無窮的意義．在有限的生命內，由于空間與能力的限制，人們經常會遇到不易解決的難題，出于各種原因，他們只能將問題轉向無窮的上帝或眾神．

哲學家們通常也會深入思考這一問題，試著去理解并解釋無窮．但究竟什么是無窮？數千年以前，古希臘哲學家已經提出更精確的問題，他們知道如何對有限數字進行加與除．但如何理解無窮過程并處理無限數字呢？

關于無窮的嚴格系統理論是晚近才由奇特的數學家康托爾創造出來的．與有限對象相比，人們過去會認為存在一個單獨的無窮集合或無窮量，獨立于所有其余的集合或量，本身并沒有什么結構．但康托爾說存在不同形式的無窮集合，而無窮集合的世界非常復雜，甚至比有限集的世界還要豐富，而且直接對其產生影響．

康托爾的理論，或者說他的觀點，已經永遠改變了數學的全部景觀，從數學的基礎直至當代數學的最前沿．因此，為了理解并欣賞數學的精妙與美，有必要接觸并熟悉無窮．

溫州大學趙煥光教授、應裕林副教授等合著的《夢想相遇無窮》，從數學、歷史以及哲學的觀點對無窮理論作了初步介紹．這是一本真正討論數學的文化著作，全書不失趣味性與可讀性，而且適合高中生與大學生閱讀．我多么希望數十年前我在大學一年級開始學習微積分時，能有機會閱讀這樣的書．

2 極限與連續

如何將無窮的觀點與數量應用到有限的函數與空間中？我們知道有無窮小與無窮大的數量與空間，而它們之間的相互作用就像一支永不停歇的探戈，刺激著數學長河川流不息的發展．其中最好的例子可能是微分與積分的對偶理論，以及將兩者聯系起來的微積分基本定理．

在這兩個理論中，極限與連續的概念都非常關鍵．如何接近才是足夠接近？多大才是足夠大？前者需要期望有多小就有多小，而后者則是需要期望有多大就有多大．這兩種情形都是無限的過程．

在定義這些概念之前，函數存在的空間必須能支持這些無限運算．在有理數集內，對達成上述目的并不完備，需要在有理數之間通過一個無限的過程將無理數添加進去構成一個沒有空洞或缺口的實數連續統集．這本著作正是從基本的集合論與實數構造的戴德金分割開始的．

3 完 備 性

從有理數集到實數集的完備可能是最早的完備化．除此之外，還有許多種，甚至可以說有無窮多種相關的完備化和緊致化方式．每個學生都知道無限級數

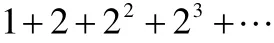
的部分和形成一個發散于實數軸上的無窮有理數列，即

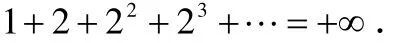
但若我們應用著名的公式

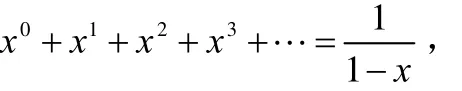
并且無視條件1||＜x，那答案將是

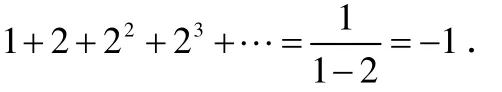
這樣，就從無限的運算中得到了有限數-1．但是正數的和怎么能是負數呢？這似乎是不可能的．然而，如果用不同的方式對有理數域進行完備化，這樣是可以正確而且可取的．可以聲明，當n 充分大時，2n是充分小的．這樣一個度量在2進制數域Q2中是成立的，Q2是p進制數域Qp的一個特殊情況，其中p是一個素數．

現代數學或數論的一個基本觀點是從Q到R的嵌入的方式，僅僅是無窮多種完備化中的一種．在這些完備化中，每一種都對應一個素數p或無窮∞．

我們需要用無窮的觀點來處理有限的有理數．上面的示例還顯示出無窮大和無窮小之間的關系可以比人們預想的更有趣．

分析的核心由微分與積分組成．我們都知道，牛頓和萊布尼茲共同發明了微積分．他們之間工作的區別是什么？在他們之前，還有誰作出了重要貢獻？在他們的工作之后又發生了什么？這本著作提供了細致且生動的論述來回答這些問題．有哪個學習微積分的學生會不想知道這其中完整的故事呢？

連續函數積分的引入可以看作是另一種形式的完備化的開始，它是一個建立在先前的無限過程之上的無限過程．比如說，給定一個有限區間[0, 1]，我們用積分定義一個在[0, 1]上的連續函數的距離，它像有理數域的情況一樣不完備．為了更好地理解這個空間，我們需要通過添加一些理想的函數來使之完備化．這個無窮過程將引導我們離開本書的話題（或者說離開我們所考慮的函數）并進入一個更廣闊的泛函分析世界，而這正是本書第一作者趙教授的專長之一．

就像將Q 完備化為R和Qp的情形一樣，若往其中添加可測函數，關于這類函數空間（巴拿赫空間和希爾伯特空間）也有無限多種完備化方法．這些概念對于目前還不了解它們的讀者而言并不十分重要，然而重要的一點是，需要以無限的過程去理解有限的事情．

4 緊致與退化

在有限與無限的對象之間還有另一個有關聯的交互．實直線R是無限的，如果有人沿著實直線的任一方向行走，他永遠都到達不了某一個點．但如果在無限中添加一個點，將R無窮的兩個方向包起來，就得到了一個圓．這里的關鍵之處是在無限中添加了一個理想的點．戴德金分割的核心之處就是在有理數之間添加理想點．

緊致化的理論以及走向無限的想法在當代數學中被廣泛地運用．有關數學對象退化的探討同樣與之相關，比如流形．佩雷爾曼（G. Perelman，1966—，俄羅斯數學家，2006年第25屆數學家大會欲為他頒發菲爾茲獎，但他拒絕領取）在三維拓撲學中著名的龐加萊猜想和莫斯托（G. D. Mostow，1923—， 美國數學家，獲2013年沃爾夫獎）強剛性重要結論的證明中都運用了這種方法．

該書常將哲學層面的討論融入到數學結論中．這種在更廣闊的視野從無窮的角度來看待事物的觀點，在生活中也非常有用．它能夠幫助人們過濾掉無關緊要的事物而突顯出什么才是人生中真正重要的，這一方法也常常被人們用到數學證明中．

5 小 結

這一著作是源于對數學的愛的勞動成果．作者試圖向讀者傳遞他們對數學的熱情以及數學與人文，諸如中國古代文獻以及中西方哲學的關聯．本書對與無窮、極限以及微積分相關的數學結論與例子給出了全面的描述．她同樣涵蓋了連續與離散數學的世界．本書可以作為微積分標準教材之外良好的補充讀物，因為書中諸多的評論與歷史事實可以拓寬讀者的視野．而從上面的論述可以看出，本書還能作為了解數學中更高深主題的橋梁．

本書的另一特點是其中引用了近幾個世紀以來著名數學家的許多名言．通過閱讀本書，讀者可以與人類歷史上的偉大心靈一起，探索數學核心概念以及它們的分支．

本書僅是趙煥光教授與他的合作者們的系列著作中的一本，這一系列著作試圖以一種友好與輕松的方式展現數學的綜合面貌．如果人們愿意挑選這一系列著作閱讀或瀏覽，將會有助于他們對數學有更好的理解．作者們承擔如此宏大工程所付出的努力及其勇氣，必將受到數學愛好者、學習數學的學生和數學研究工作者的欽佩與贊賞．

注：《夢想相遇無窮》為科學出版社《文化數學欣賞叢書》的第3本．該系列叢書共6本，分別為《生活相遇數學》、《人生相遇函數》、《夢想相遇無窮》、《真理相遇統計》、《文明相遇幾何》以及《智慧相遇代數》．目前，《生活相遇數學》、《人生相遇函數》與《夢想相遇無窮》已出版．

致謝：本文的主體內容為季理真教授為《夢想相遇無窮》所作的序言，由章勤瓊譯成中文，文中的第一段及最后的注為譯者在與作者討論后所加．溫州大學王瑋明教授等對譯文提出了寶貴意見，在此一并感謝．

Golden Bridge between Infinite and Finite: Mathematics

JI Li-zhen1, ZHANG Qin-qiong2,3
(1. University of Michigan, Michigan USA, 48109; 2. Wenzhou University, Zhejiang Wenzhou 325035, China; 3. Nanjing Normal University, Jiangsu Nanjing 210023, China)

The notion of infinity is of central importance in mathematics. In this article, we start from the book “When Dreams Encounter Infinity” and discuss how several related concepts such as completion, compactification, degeneration lead to major theories and theorems in contemporary mathematics.

infinite; limit; completion; compactification; degeneration

G40-03

：A

：1004–9894（2014）02–0093–02

[責任編校：周學智]

2014–01–07

季理真（1964—），男，浙江溫州人，美國密歇根大學教授，浙江大學光彪特聘教授，主要從事幾何、拓撲、數論及數學交叉學科等研究．章勤瓊為本文通訊作者．