Grain型級聯反饋移存器的非奇異性判定

王秋艷，金晨輝

?

Grain型級聯反饋移存器的非奇異性判定

王秋艷，金晨輝

(解放軍信息工程大學三院，鄭州 450004)

Grain算法是歐洲序列密碼工程eSTREAM最終入選的面向硬件實現的3個序列密碼算法之一，它由2個反饋移存器和前饋函數組成，能有效抵御基于線性反饋移存器的序列密碼攻擊。針對以Grain算法為特例的Grain型級聯反饋移存器的非奇異性判定問題，給出Grain型級聯反饋移存器在初始化過程和密鑰流生成過程中，狀態刷新變換均構成雙射的充分條件，并通過反例說明對于有限域上的Grain型級聯反饋移存器，即使所使用的2個移存器都是非奇異的，并且前饋函數滿足相應性質，其狀態刷新變換仍可能不構成雙射。利用Grain v1算法驗證了該非奇異性判定結果的正確性。

序列密碼；Grain算法；非線性反饋移存器；非奇異性；狀態刷新變換；雙射性

1 概述

線性反饋移存器的輸出序列具有良好的密碼學性質，目前很多序列密碼算法都由線性反饋移存器和非線性前饋函數(或非線性有記憶變換)構成。然而，由于線性反饋移存器的輸出信號之間存在線性制約性，從而產生很多針對基于線性反饋移存器設計的序列密碼的攻擊方法，如代數攻擊[1]、快速相關攻擊[2]等，促使人們尋找新的序列密碼結構。在eSTREAM工程中，最終勝出的3個面向硬件實現的序列密碼算法Grain算法[3]、Trivium算法[4]和Mickey算法[5]都是基于非線性反饋移存器設計。目前，基于非線性反饋移存器的設計已逐漸發展為序列密碼設計的重要方式。

Grain算法[6-7]是一個典型的基于非線性反饋移存器設計的序列密碼算法，為保證Grain序列密碼算法的輸出序列具有良好的密碼學性質，Grain算法通過利用一個周期達到最大的線性反饋移存器控制一個非線性反饋移存器的方法設計其亂源結構。這種將線性反饋移存器和非線性反饋移存器有機結合的方式，為序列密碼的設計提供了一個典型的模型。文獻[8]對該模型的安全性進行了分析，對這種模型給出了一種區分攻擊。文獻[9]對該模型進行了代數攻擊和相關攻擊。文獻[10]研究了其輸出序列的周期性質。

反饋移存器的非奇異性[11]，也就是反饋移存器的狀態刷新變換構成雙射，是序列密碼設計中對反饋移存器的基本要求。如果反饋移存器是奇異的，則其狀態圖將出現分叉現象，從而存在2個能產生相同的后續狀態的移存器狀態，此時基于該移存器設計的序列密碼可能存在等效密鑰，甚至可能遭遇基于相關(密鑰-IV)對的差分攻擊[12]。因此，在設計序列密碼時，應該確保反饋移存器的非奇異性，以避免可能存在的安全隱患。

本文研究以Grain算法為特例的一類反饋移存器模型(稱為Grain型級聯反饋移存器)的非奇異性判定問題。給出能使其在初始化過程和密鑰流生成過程中的狀態刷新變換都構成雙射的充分條件，并通過反例證明在一定條件下Grain型級聯反饋移存器的狀態刷新函數不能構成雙射。

2 Grain型級聯反饋移存器簡介

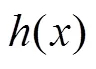
圖1 Grain型級聯反饋移存器的結構框圖

在初始化過程和密鑰流生成過程2種情形下，Grain型級聯反饋移存器采取2種不同的狀態刷新方式：

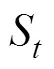
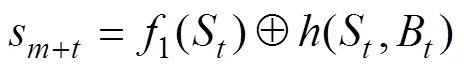
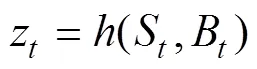
3 Grain型級聯反饋移存器的非奇異性研究

首先給出Grain型級聯反饋移存器在密鑰流生成過程中狀態刷新變換構成雙射的充分條件。

定理1 設在Grain型級聯反饋移存器中FSR1是非奇異的，則以下結論等價：

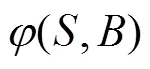
(2)Grain型級聯反饋移存器中FSR2是非奇異的；

證明：由引理可知，結論(2)和結論(3)等價。下文證明結論(1)與結論(3)等價。

設結論(3)成立。由于Grain型級聯反饋移存器的狀態刷新變換為：

當以下等式成立時：

由Grain型級聯反饋移存器的狀態刷新變換定義可知：

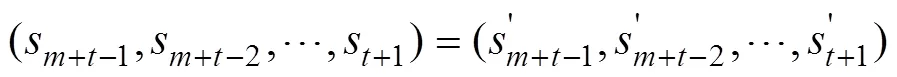
且有：

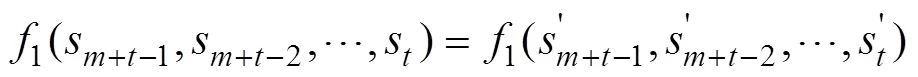
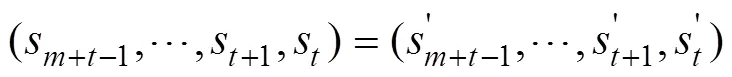
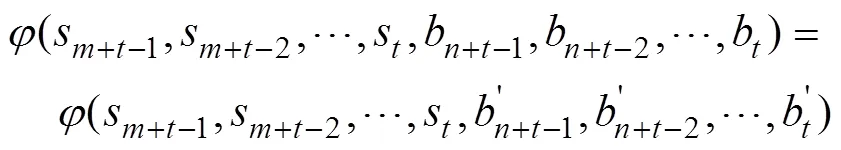
由此即知結論(1)與結論(3)等價。

然后給出Grain型級聯反饋移存器在初始化過程中狀態刷新變換構成雙射的充分條件。

定理2 設在Grain型級聯反饋移存器中FSR1和FSR2都是非奇異的，如果函數：

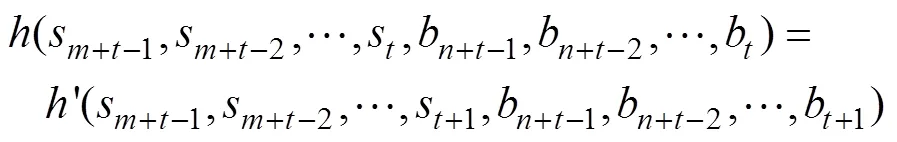
證明：Grain型級聯反饋移存器在初始化過程的狀態刷新變換為：

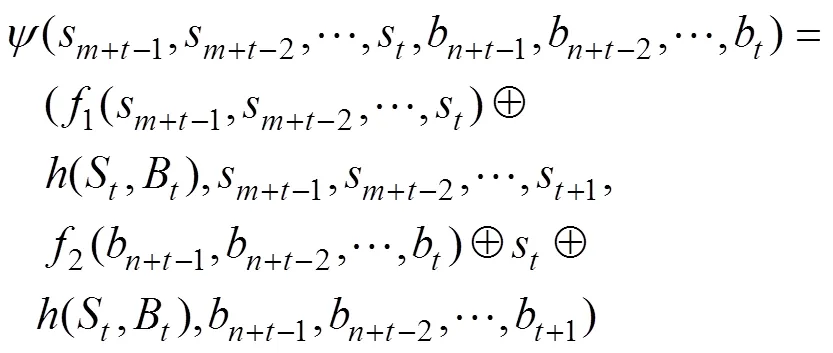
其中：

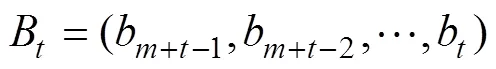
假設：

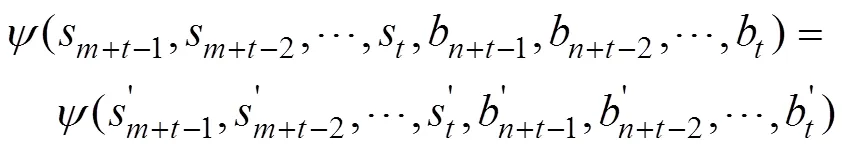
由Grain型級聯反饋移存器的狀態刷新變換定義可知：

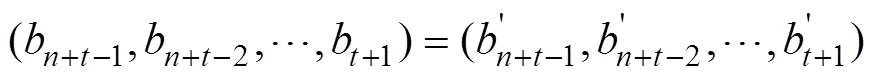
且有：

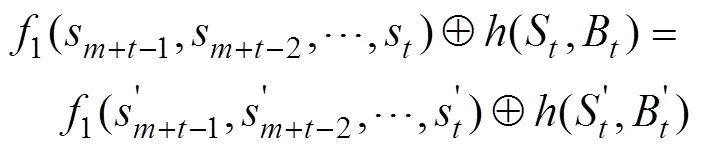
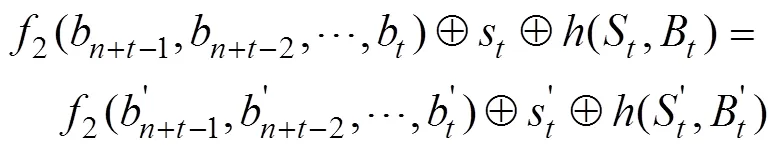
由定理1和定理2可知，為保證Grain型級聯反饋移存器的狀態刷新函數構成雙射，只需將Grain型級聯反饋移存器中的2個FSR都設計成非奇異反饋移存器，且前饋函數的輸入變量都不抽自2個FSR的最低級即可。

定理3表明，即使前饋函數的輸入變量從FSR2的最低級抽取，在一定條件下仍可保證Grain型級聯反饋移存器的狀態刷新函數構成雙射。

定理3 設在Grain型級聯反饋移存器中FSR1和FSR2是非奇異的，如果函數：

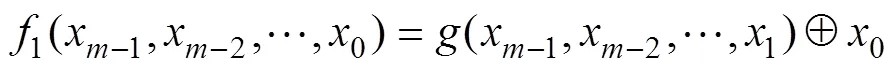
證明：Grain型級聯反饋移存器在初始化過程的狀態刷新變換為：

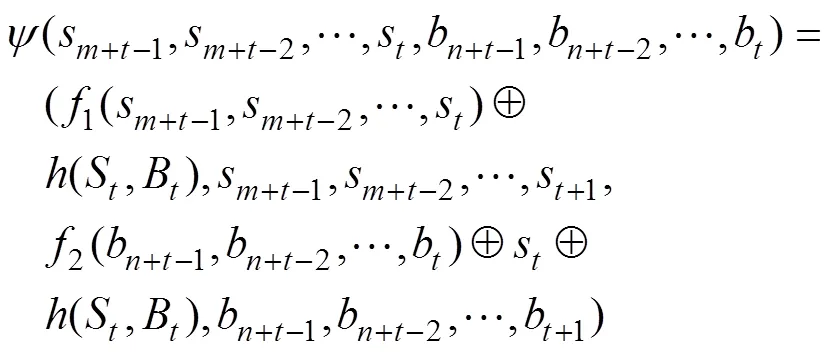
其中：

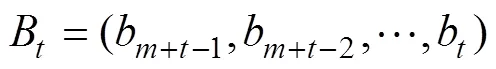
假設：

由Grain型級聯反饋移存器的狀態刷新變換定義可知：

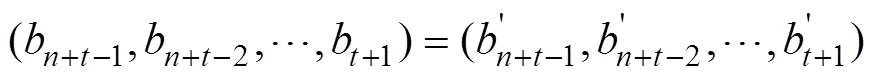
且有：

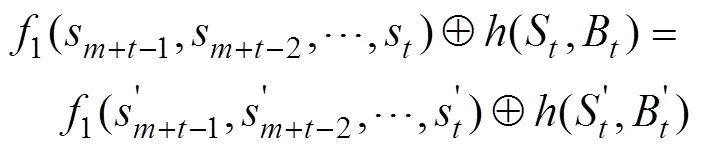
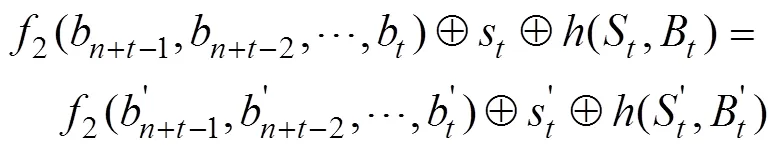
下面給出定理3的一個反例，當前饋函數滿足定理3的條件，輸入變量不從FSR2的最低級抽取，如果FSR1的反饋函數不滿足定理3的條件，則Grain型級聯反饋移存器的狀態刷新函數就有可能構不成雙射。

定理4 設Grain型級聯反饋移存器中FSR1和FSR2的反饋函數滿足：

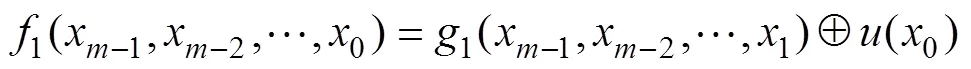
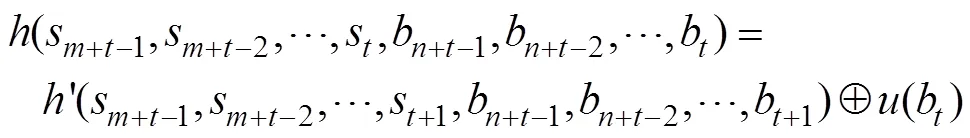
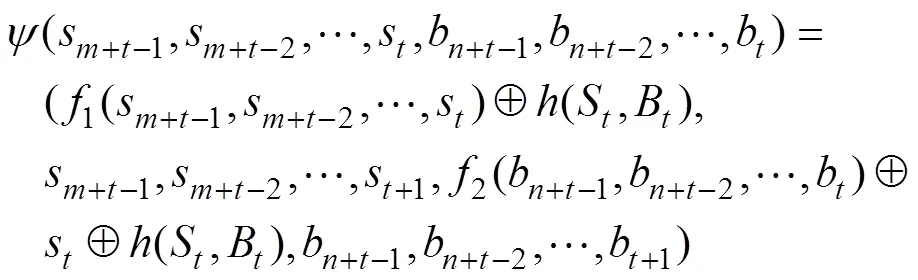
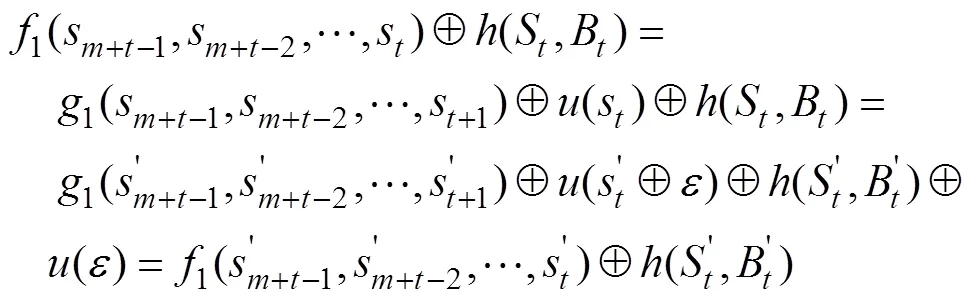
說明：

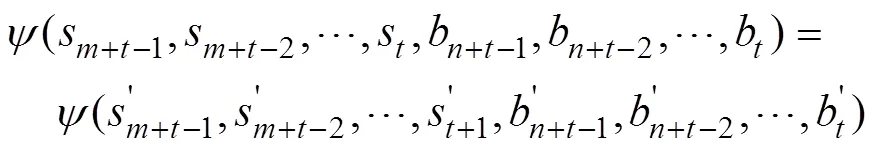
最后證明Grain v1算法在初始化過程和密鑰流生成過程的狀態刷新函數都是雙射的。

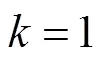
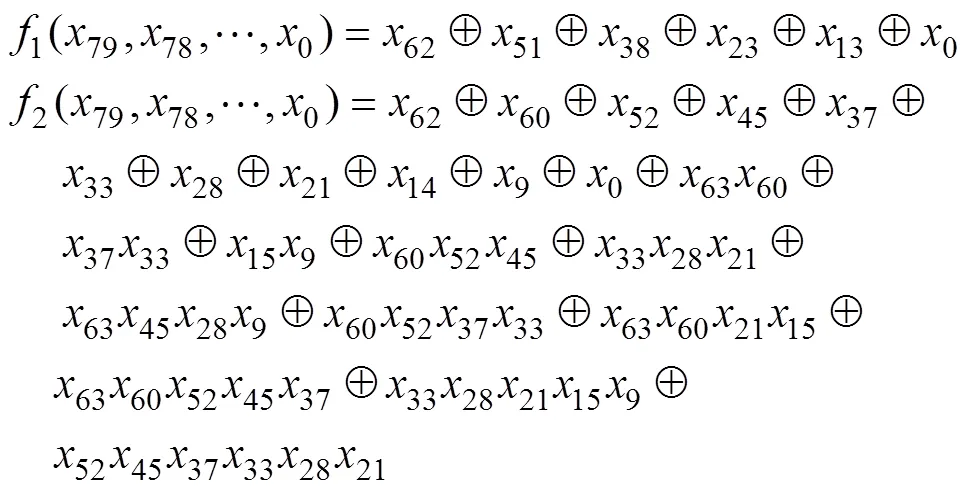
定理5 Grain v1算法在初始化過程和密鑰流生成過程的狀態刷新變換都是雙射的。

4 結束語

本文研究了Grain型級聯反饋移存器的非奇異性問題，給出了其在初始化過程和密鑰流生成過程中狀態刷新變換構成雙射的2個充分條件，并舉例說明了在一定條件下其狀態刷新變換可能不構成雙射，這些結果對于基于Grain型級聯反饋移存器的序列密碼的設計和分析具有實際的應用價值。通過本文分析可知，Grain型級聯反饋移存器存在潛在弱點，必須謹慎選擇其反饋函數和濾波函數以保證其安全性。在下一步的工作中，將進一步對Grain型級聯反饋移存器的密碼學性質進行分析，并研究該類移存器的構造問題。

[1] Courtois N T, Meier W. Algebraic Attacks on Stream Ciphers with Linear Feedback[C]//Proc. of EUROCRYPT’03. Warsaw, Poland: Springer-Verlag, 2003: 345-359.

[2] Meier W, Staffelbach O. Fast Correlation Attacks on Stream Ciphers[J]. Journal of Cryptology, 1989, l(3): 159-176.

[3] Hell M, Johansson T, Meier W. Grain——A Stream Cipher for Constrained Environments[EB/OL]. (2005-06-22). http://www. ecrypt.eu.org/stream/ciphers/grain/grain.pdf.

[4] de Cannière C. Trivium: A Stream Cipher Construction Inspired by Block Cipher Design Principles[C]//Proc. of ISC’06. [S. l.]: Springer-Verlag, 2006: 171-186.

[5] Babbage S. The Stream Cipher MICKEY-128 2.0[EB/OL]. (2006-08-18). http://www.ecrypt.eu.org/stream/p2ciphers/mickey128/ mickey128_p2.pdf.

[6] Maximov A. Cryptanalysis of the “Grain” Family of Stream Cipher[C]//Proc. of ASIACCS’06. New York, USA: ACM Press, 2006: 283-288.

[7] 宋海欣, 范修斌, 武傳坤, 等. 流密碼算法Grain的立方攻擊[J]. 軟件學報, 2012, 23(1): 171-176.

[8] 黃小莉, 武傳坤. 對一種新的序列密碼結構的密碼分析[J]. 軟件學報, 2008, 19(5): 1256-1264.

[9] Berbain C, Gilbert H. Algebraic and Correlation Attacks Against Linearly Filtered Non Linear Feedback Shift Registers[C]//Proc. of SAC’09. [S. l.]: Springer-Verlag, 2009: 184-198.

[10] Hu Honggang. Periods on Two Kinds of Nonlinear Feedback Shift Registers with Time Varying Feedback Functions[J]. International Journal of Foundations of Computer Science, 2011, 22(6): 1317-1329.

[11] Lai Xuejia. Condition for the Nonsingularity of a Feedback Shift Register over a General Finite Field[J]. IEEE Transac- tions on Information Theory, 1987, 33(5): 747-749.

[12] Wu Hongjun, Huang Tao, Nguyen P H. Differential Attacks Against Stream Cipher ZUC[C]//Proc. of ASIACRYPT’12. Beijing, China: [s. n.], 2012: 262-277.

編輯 陸燕菲

Criteria forNonsingularityof Grain-like Cascade Feedback Shift Register

WANG Qiu-yan, JIN Chen-hui

(The Third Institute, PLA Information Engineering University, Zhengzhou 450004, China)

Grain cipher is one of the 3 final hardware-oriented stream ciphers of the eSTREAM project, it is based on two feedback shift registers and a filtering function, and it can effectively resist stream cipher attacks based on linear feedback shift register. In this paper, the nonsingularity of the Grain-like cascade feedback shift registers is investigated, the sufficient conditions of state refresh transformations in initialization phase and key stream generation phase being bijective is given. As a counterexample, for the word-oriented Grain-like cascade feedback shift registers, even if the two feedback shift registers are both nonsingular, and the filtering function satisfies proper conditions, the state update transformation can also be nonbijective. It proves the result of criteria for nonsingularity by using Grain v1 algorithm.

stream cipher; Grain algorithm; nonlinear feedback shift register; nonsingularity; state refresh transformation; bijectivity

1000-428(2014)03-0167-04

A

TN918.1

國家自然科學基金資助項目(61272488, 61272041)。

王秋艷(1985－)，女，博士研究生，主研方向：密碼學；金晨輝，教授、博士生導師。

2013-03-01

2013-04-02 E-mail：wangqiuyan06@gmail.com

10.3969/j.issn.1000-3428.2014.03.034