基于空域?yàn)V波的雷達(dá)目標(biāo)二維散射中心快速提取

張 肖 周建江 汪 飛

?

基于空域?yàn)V波的雷達(dá)目標(biāo)二維散射中心快速提取

張 肖 周建江*汪 飛

(南京航空航天大學(xué)電子信息工程學(xué)院 南京 210016)

針對(duì)幾何繞射(GTD)模型，該文提出一種基于空域?yàn)V波的2維散射中心參數(shù)快速提取方法。該方法利用空域?yàn)V波過程將2維散射中心參數(shù)提取問題分解為多個(gè)1維散射中心提取問題，并利用1維旋轉(zhuǎn)不變技術(shù)(1D-ESPRIT)來估計(jì)散射中心各維參數(shù)，最后利用最小歐氏距離實(shí)現(xiàn)2維參數(shù)的配對(duì)。與基于2維旋轉(zhuǎn)不變技術(shù)(2D-ESPRIT)的方法相比，該方法避免了高維數(shù)的特征值分解，因而可以顯著地降低計(jì)算的復(fù)雜度。仿真實(shí)驗(yàn)表明，與2D-ESPRIT高分辨算法相比，該方法不僅能夠顯著降低計(jì)算量，并且還能獲得較好的估計(jì)精度，可以有效地用于提取目標(biāo)散射中心參數(shù)信息。

雷達(dá)；散射中心；幾何繞射(GTD)模型；空域?yàn)V波；旋轉(zhuǎn)不變技術(shù)

1 引言

本文主要針對(duì)幾何繞射(GTD)模型[12]，提出了一種基于空域?yàn)V波的散射中心提取方法。該方法利用空域?yàn)V波將2維散射中心提取分解為多個(gè)1維散射中心提取的問題，并用1D-ESPRIT分別對(duì)各維參數(shù)進(jìn)行估計(jì)，最后根據(jù)位置參數(shù)粗估計(jì)與精確估計(jì)之間的近似關(guān)系，通過最小歐氏距離實(shí)現(xiàn)配對(duì)。因此，本文方法無需構(gòu)造高維數(shù)的增廣矩陣，從而避免了高維數(shù)的特征值分解，大大降低了計(jì)算量。

2 2維GTD散射模型

以頻率步進(jìn)雷達(dá)為例，根據(jù)幾何繞射理論(GTD)，在寬帶小轉(zhuǎn)角條件下，忽略角度依賴性，目標(biāo)總的回波可以表示為[10]

經(jīng)極坐標(biāo)插值后回波數(shù)據(jù)可以近似為

3 基于GTD模型的2維散射中心快速提取方法

3.1 基于空域?yàn)V波的位置參數(shù)及類型參數(shù)的快速估計(jì)

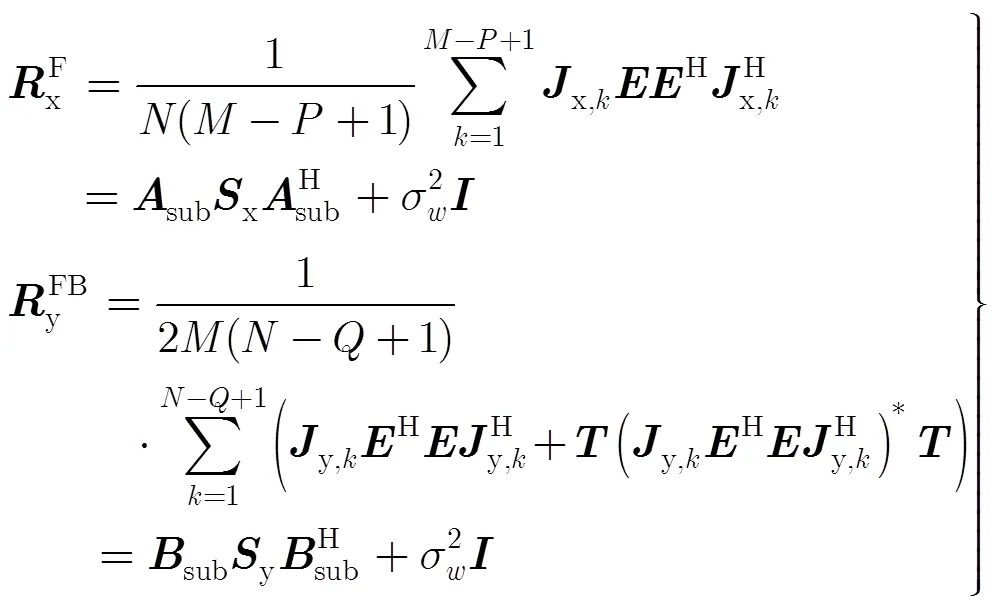
由于在多數(shù)情況下，各散射中心在距離向或方位向上的位置相近，此時(shí)以上方法可能無法單獨(dú)在距離向或方位向上分辨這些相近散射中心，從而導(dǎo)致無法獲得精確的距離向或方位向位置參數(shù)估計(jì)。所以由式(5)得到的只是位置參數(shù)的粗估計(jì)，且不是一一對(duì)應(yīng)的。

3.1.2空域?yàn)V波分組 根據(jù)式(5)得到的兩組散射中心位置參數(shù)的粗估計(jì)，可以構(gòu)造相應(yīng)的空域?yàn)V波器組：

利用式(6)得到的空域?yàn)V波器組對(duì)原數(shù)據(jù)矩陣進(jìn)行濾波分組，可得

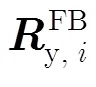
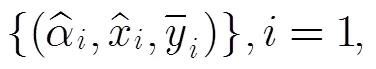
3.2 算法流程以及計(jì)算量分析

綜上所述，本文方法可以總結(jié)為以下幾個(gè)步驟：

(4)利用式(10)，實(shí)現(xiàn)散射中心參數(shù)精確估計(jì)之間的配對(duì)；

(5)最后利用最小二乘法，得到散射中心散射強(qiáng)度的估計(jì)。

4 仿真實(shí)驗(yàn)及性能分析

為了驗(yàn)證本文方法的有效性，對(duì)本文方法和2D-ESPRIT方法[10]的估計(jì)性能作了仿真實(shí)驗(yàn)研究。

圖1 復(fù)乘運(yùn)算量比較

仿真1比較了在不同帶寬、不同信噪比下兩種方法的估計(jì)精度；仿真2驗(yàn)證了本文方法對(duì)復(fù)雜目標(biāo)回波數(shù)據(jù)的有效性。

表1散射中心參數(shù)取值

序號(hào)距離向位置x(m)方位向位置y(m)散射中心類型參數(shù)散射強(qiáng)度A 1-1.00-1.00-1.01 2-0.950 1.01 3-1.00 1.00-1.01 4 1.00 1.08-0.51 5 1.05-1.00 0.51 6 3.00-1.0001 7-0.50 1.0301

仿真2 選取南京航空航天大學(xué)目標(biāo)特性研究中心提供的AMG158導(dǎo)彈模型回波數(shù)據(jù)作為實(shí)驗(yàn)數(shù)據(jù)，測(cè)量條件為：起始頻率為9 GHz，帶寬為800 MHz，頻率采樣點(diǎn)數(shù)均為=51；觀測(cè)方位角范圍為12.5o~17.5o(機(jī)頭方向?yàn)?o)，采樣點(diǎn)數(shù)為=51。

圖6所示為該模型的2維傅里葉變換成像結(jié)果。由于帶寬和轉(zhuǎn)角的限制，導(dǎo)致成像分辨率較低。圖7和圖8所示分別為采用2D-ESPRIT算法和本文方法得到的散射中心位置參數(shù)。從圖7和圖8不難看出，本文方法與2D-ESPRIT算法得到的散射中心位置基本一致，且兩種方法得到的散射中心位置均與目標(biāo)2維傅里葉變換成像結(jié)果吻合良好。表2所示為本文方法的估計(jì)結(jié)果，可見所提取的散射中心能較為準(zhǔn)確地反映目標(biāo)的尺寸以及強(qiáng)弱散射中心的分布。實(shí)驗(yàn)結(jié)果很好地驗(yàn)證了本文方法對(duì)復(fù)雜目標(biāo)回波數(shù)據(jù)的有效性。

5 結(jié)論

本文采用了能夠精確描述目標(biāo)高頻電磁散射特性的GTD模型來表征雷達(dá)目標(biāo)的散射特性。并針對(duì)GTD模型，提出了一種高估計(jì)精度、低運(yùn)算復(fù)雜度的散射中心參數(shù)快速提取方法。該方法利用1D-ESPRIT的高分辨特性和空域?yàn)V波分組技術(shù)實(shí)現(xiàn)了2維散射中心參數(shù)的估計(jì)，避免了高維數(shù)的特征值分解，實(shí)現(xiàn)了散射中心的位置、類型以及散射強(qiáng)度的快速估計(jì)。從仿真實(shí)驗(yàn)可以看出，相比2D- ESPRIT算法，本文方法不僅具有相似的估計(jì)性能，而且顯著地降低了計(jì)算運(yùn)算量，同時(shí)利用前后向空間平滑技術(shù)提高了方位向位置的估計(jì)精度，并且在遇到散射中心距離向位置或方位向位置重復(fù)或近似時(shí)，同樣能夠?qū)崿F(xiàn)正確的配對(duì)。

圖3 400 MHz和600 MHz帶寬下方位向位置估計(jì)的平均均方根誤差

圖4 400 MHz和600 MHz帶寬下類型參數(shù)估計(jì)的平均正確率

圖5 400 MHz和600 MHz帶寬下散射強(qiáng)度估計(jì)的平均均方根誤差

圖6 2維傅里葉變換成像結(jié)果

圖7 2D-ESPRIT算法提取結(jié)果

圖8 本文方法提取結(jié)果

表2本文方法的參數(shù)估計(jì)結(jié)果

序號(hào)123456789 距離向位置(m) 1.8596 1.7474 1.1741 0.7353 0.6548-1.1017-1.4333-1.9680-1.9273 方位向位置(m)-0.4722-0.2827-0.0546-0.2722-0.0850 0.4593 0.3532 0.5871 0.1583 歸一化強(qiáng)度 0.4074 0.7869 0.6647 0.2640 0.7031 0.6534 0.5023 0.9866 1.0000

[1] 黃培康, 殷紅成, 許小劍. 雷達(dá)目標(biāo)特性[M]. 北京: 電子工業(yè)出版社, 2005, 3: 229-278.

[2] Zhou Jian-xiong, Shi Zhi-guang, Xiao Cheng,.. Automatic target recognition of SAR images based on global scattering center model[J]., 2011, 49(10): 3713-3729.

[3] 付強(qiáng), 周劍雄, 秦敬喜, 等. 雷達(dá)目標(biāo)散射中心模型反演及其在識(shí)別中的應(yīng)用[J]. 系統(tǒng)工程與電子技術(shù), 2011, 33(1): 48-52.

Fu Qiang, Zhou Jian-xiong, Qin Jing-xi,.. Global scattering center model extraction and its application in radar target recognition[J]., 2011, 33(1): 48-52.

[4] Gudnason J, Cui Jing-jing, and Brookes M. HRR automatic target recognition from superresolution scattering center features[J]., 2009, 54(4): 1512-1524.

[5] 唐濤, 粟毅. 散射中心特征序貫匹配的SAR圖像目標(biāo)識(shí)別方法[J]. 系統(tǒng)工程與電子技術(shù), 2012, 34(6): 1131-1135.

Tang Tao and Su Yi. Object recognition in SAR imagery using sequential feature matching of scattering centers[J]., 2012, 34(6): 1131-1135.

[6] Ismail J. Scattering features for target recognition using finite rate of innovation model[C]. IEEE International Symposium on Antennas and Propagation (APSURSI2012), Chicago, 2012: 1-2.

[7] 葉礬, 何峰, 張永勝, 等. 基于GTD模型的多雷達(dá)信號(hào)二維融合[J]. 電子與信息學(xué)報(bào), 2011, 33(1): 55-59.

Ye Fan, He Feng, Zhang Yong-sheng,.. Two-dimensional fusion of multi-radar signals based on GTD model[J].&, 2011, 33(1): 55-59.

[8] 周劍雄, 石志廣, 胡磊, 等. 基于頻率稀疏非均勻采樣的雷達(dá)目標(biāo)一維高分辨成像[J]. 電子學(xué)報(bào), 2012, 40(5): 926-934.

Zhou Jian-xiong, Shi Zhi-guang, Hu Lei,.. Radar target one dimensional high resolution imaging based on sparse and non-uniform samplings in frequency domain[J]., 2012, 40(5): 926-934.

[9] Quinquis A, Radoi E,.. Some radar imagery results using superresolution techniques[J]., 2004, 52(5): 1230-1244.

[10] 王菁, 周建江, 汪飛. 基于GTD模型的目標(biāo)二維散射中心提取[J]. 電子與信息學(xué)報(bào), 2009, 31(4): 958-962.

Wang Jing, Zhou Jian-jiang, and Wang Fei. 2D scattering centers extraction of objects based on GTD model[J].&, 2009, 31(4): 958-962.

[11] Wei Shao-ming, Yu Juan,.. State space processing based approach for extracting scattering center parameters of high resolution SAR target[J]., 2012, 7(12): 43-51.

[12] Potter L C, Chiang Da-ming,A GTD-based parametric model for radar scattering[J]., 1995, 43(10): 1058-1067.

[13] Roy R and Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J].,, 1989, 37(7): 984-995.

[14] Li Ming-hui and Lu Yi-long. Dimension reduction for array processing with robust interference cancellation[J]., 2006, 42(1): 103-112.

[15] Lin Jen-der, Fang Wen-hsien, Wang Yung-yi,.. FSF- MUSIC for joint DOA and frequency estimation[J]., 2006, 54(12): 4529-4542.

張 肖： 男，1985年生，博士生，研究方向?yàn)槔走_(dá)信號(hào)處理等.

周建江： 男，1962年生，教授，博士生導(dǎo)師，主要研究方向?yàn)槔走_(dá)信號(hào)處理、目標(biāo)特征的提取與控制.

汪 飛： 男，1976年生，博士，副教授，研究方向?yàn)樽V分析、信號(hào)特征參量估計(jì)等.

Fast Extraction of Radar Target 2D Scattering Centers Based on Spatial Filtering

Zhang Xiao Zhou Jian-jiang Wang Fei

(,,210016,)

For a model derived from the Geometrical Theory of Diffraction (GTD), a fast method based on spatial filtering is proposed to extract parameters of two-dimensionalscattering centers. The proposed method utilizes spatial filtering process todecompose two-dimensionalscattering centers extraction into several times of one-dimensional scattering centers extraction, in which the one-dimensional Estimation of Signal Parameters via Rotational Invariance Techniques (ESPRIT) is employed to estimate the parameters of scattering centers for each dimensional independently. Finally, the pair-matching of two-dimensional parameters is accomplished by searching the minimums of Euclidean distance. Compared with the method based on two-dimensional ESPRIT, the proposed method does not need high-dimensional eigenvalue decomposition, thus the computational complexity is significantly reduced.Simulation resultsshow that the proposed methodnot onlyreduces greatly thecomputational burden, but also keeps high accuracy of parameter estimation compared with 2D-ESPRIT algorithm, and it is proved to be effective in scattering center extraction.

Radar; Scattering center; Geometric Theory of Diffraction (GTD) model; Spatial filtering; Estimation of Signal Parameters viaRotational Invariance Techniques (ESPRIT)

TN957.51

A

1009-5896(2014)03-0523-06

10.3724/SP.J.1146.2013.00365

2013-03-22收到，2013-11-22改回

國家部級(jí)基金和江蘇高校優(yōu)勢(shì)學(xué)科建設(shè)工程資助課題

周建江 zx6632910@hotmail.com