磁流變沖擊后坐控制系統試驗研究

張莉潔，常家東，王 炅，程廣偉

（1．洛陽理工學院機械工程系，河南 洛陽 471023；2．南京理工大學機械工程學院，南京 210094）

磁流變沖擊后坐控制系統試驗研究

張莉潔1，常家東1，王 炅2，程廣偉1

（1．洛陽理工學院機械工程系，河南 洛陽 471023；2．南京理工大學機械工程學院，南京 210094）

針對磁流變阻尼器用于火炮后坐緩沖時對響應時間的嚴苛要求，對磁流變沖擊后坐控制系統進行沖擊試驗研究。對設計的磁流變阻尼器進行固定電流下沖擊特性試驗，獲得輸出阻力模型。對阻尼器線圈電流及輸出阻力響應時間分別進行試驗測試，提出磁流變沖擊后坐軌跡跟蹤控制系統方案，期望可控阻力能準確跟蹤理想阻力曲線。通過用固定曲線無反饋控制及雙閉環反饋控制對磁流變后坐控制系統進行3 g、4 g藥量沖擊試驗結果比較知，采用反饋控制能顯著減小磁流變后坐阻力響應時間，獲得快速跟蹤性能，后坐阻力充滿度更好。后坐位移相同時可減小后坐阻力峰值；后坐阻力峰值相同時可顯著減小后坐位移。由4g藥量中后坐阻力曲線下滑結果分析知，阻尼力可調系數作為重要特性參數在進行磁流變阻尼器結構設計時必須足夠大。

磁流變阻尼器；沖擊載荷；反后坐裝置；響應時間；軌跡跟蹤系統

以磁流變液為介質的磁流變阻尼器（Magneto-rheological dampers）因具有結構簡單、阻尼力實時可控、能耗低等特點在航空及武器裝備緩沖系統中應用前景廣闊［1－2］。將磁流變阻尼器用于火炮反后坐裝置代替制退機并實時控制，以獲得理想后坐動態特性、提高火炮發射的穩定性及射擊精度。高沖擊載荷下火炮后坐過程非常迅速，僅幾百毫秒。在極短時間內實現后坐阻力實時可控對磁流變阻尼器控制系統響應時間提出嚴苛要求。需對磁流變阻尼器響應時間進行論證。對用于汽車、車削及轉子等減振系統的磁流變減振器響應時間均有詳細研究及論述［3－6］，對磁流變沖擊后坐緩沖應用研究大多集中于后坐控制方法論述［7－9］。而普遍忽略評價控制系統優劣的重要指標即動態響應時間，缺乏明確闡述及相關試驗論證，磁流變沖擊后坐控制系統本質仍有待揭示。

本文針對沖擊載荷下磁流變阻尼器響應時間問題，利用阻尼器輸出阻力模型對響應時間試驗測試及分析。考慮響應時間提出磁流變沖擊后坐跟蹤控制系統設計方案及雙閉環反饋控制算法，以提高系統響應時間及抗干擾能力為目的，期望后坐阻力達到理想的跟蹤控制效果；并通過沖擊試驗驗證控制效果及后坐動態特性。

1 磁流變阻尼器沖擊動態特性分析

1.1 固定電流沖擊試驗

沖擊試驗臺架見圖1，僅安裝磁流變阻尼器，未安裝復進裝置。磁流變阻尼器為長行程單出桿單筒式，內徑50 mm。阻尼器缸筒安裝在軸套內與后坐配重質量塊固連，活塞桿與地面支座固連。試驗通過密爆發生器產生沖擊源，阻尼器缸筒受沖擊載荷后帶動后坐配重質量塊沿導軌產生相對活塞桿的后坐運動。緩沖器起保護臺架作用，當后坐運動到達緩沖器位置時提供緩沖，避免剛性碰撞。臺架最大行程600 mm。測試缸筒后坐時動力參數。

圖1 磁流變阻尼器沖擊試驗臺架實物圖Fig．1 Impact test facility for MR damper

沖擊后坐中磁流變阻尼器作為緩沖器將瞬間產生的極大能量沖擊載荷轉化為作用時間長、峰值低的后坐阻力作用于機架。后坐過程運動微分方程［10］為

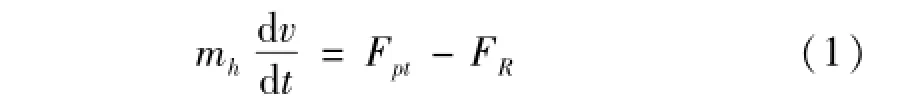
式中：Fpt為沖擊載荷；mh為后坐質量；FR為后坐阻力；FR＝FMR＋FФ＋Ff，FMR為磁流變阻尼器阻尼力，由安裝在支座與活塞桿上的力傳感器測得，FФ為復進機力，未安裝時FФ＝0，Ff＝200 N為后坐接觸構件間摩擦力。

由動能定理，后坐行程為λ時，為使后坐阻力FR總功抵消沖擊載荷總功，應滿足

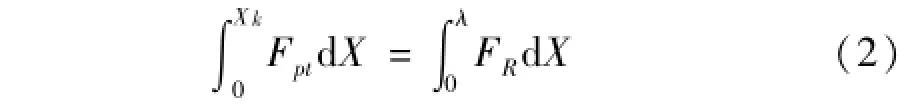
相同后坐位移λ時為使FRmax最小，應使FR＝常數。后坐曲線“充滿”矩形面積，即應保證良好的充滿度，見圖2。采用磁流變阻尼器代替傳統制退機，以期利用其阻力實時可控性改善后坐動態特性。

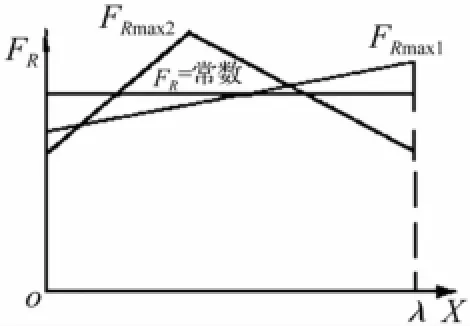
圖2 做功面積相同的幾種后坐阻力變化規律Fig．2 Variation rules of recoil force at the same power area

用3．2 g火藥量分別對磁流變阻尼器線圈施加0 A、0．8 A、1．5 A、2 A固定電流，獲得后坐諸元曲線，見圖3。由于爆炸沖擊力遠大于后坐阻力，沖擊瞬間后坐阻力可忽略不計。由沖量定理知，沖擊沖量大小決定后坐速度峰值。由圖3（a）看出，后坐速度峰值可判斷各次試驗火藥量存在差別，各次沖擊力不完全相等；且后坐過程結束前速度反向，說明阻尼器在此處微量反彈，此因磁流變阻尼器的滯回特性所致。圖3（b）為阻尼力與速度比較，后坐速度達到峰值時后坐阻力峰值同時出現，且阻力峰值隨所加電流增大而增大，顯示磁流變阻尼器輸出阻力的可控性。

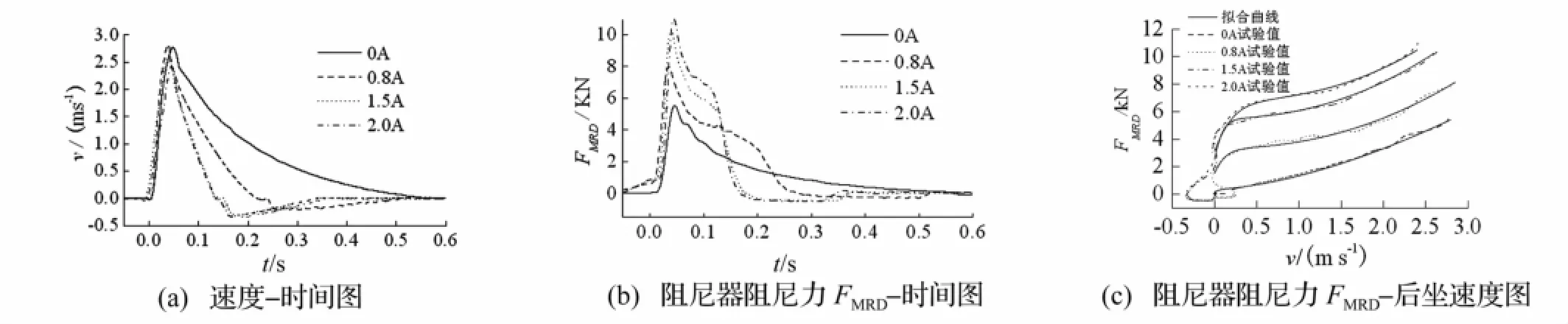
圖3 不同電流后坐諸元曲線圖Fig．3 Curves of v，FMRD－t，FMRD－v for MR recoil damper at different currents

1.2 建模分析

速度達峰值后因慣性力作用輸出阻力與后坐速度vr成指數函數關系［11］，見圖3（c）。通過曲線擬合及參數辨識可得磁流變阻尼器輸出阻力簡化模型［11－12］，即

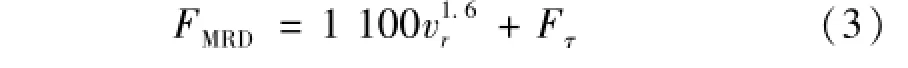
式中：vr為后坐速度。該模型將磁流變阻尼力分為兩部分，第一部分與后坐速度vr有關，反映流體粘滯阻尼特性，稱粘性阻尼力，記Fη；第二部分Fτ與磁流變液屈服強度τy有關，其大小受工作電流控制，稱可調庫侖阻尼力。Fτ為磁流變阻尼器阻尼力可控部分［12］。

該模型雖與實測曲線有一定誤差，但可實現阻尼力隨速度、電流變化的完全解耦；遵循復雜問題簡單化、去末求本思想，該模型在對磁流變阻尼力實施快速線性控制算法時體現出重要的實用價值。

1.3 后坐控制原理論述

由圖3（b）看出，在固定電流下后坐速度峰值過后磁流變輸出阻力FMRD隨時間逐漸下滑，充滿度不好。因此，通過施加適當工作電流增大可調阻尼力Fτ，補償粘性阻力隨后坐速度下降，從而保證充滿度飽滿。磁流變沖擊后坐控制目的在于使可調庫倫阻力Fτ按理想曲線輸出，屬于跟蹤控制問題，要求系統快速響應。

2 磁流變阻尼器沖擊響應時間測定

2.1 電磁電路響應時間測定

磁流變阻尼器輸出阻力響應時間具體指［13］磁流變阻尼器從感知擾動（輸入控制信號變化）至產生穩定的阻力所需時間。本文在階躍輸入下對磁流變阻尼器電磁電路及輸出阻力響應時間分別進行測試分析。

磁流變阻尼器電流驅動電路采用脈寬調制PWM（Pulse Width Modulation）電流驅動技術，通過PWM信號對磁流變阻尼器勵磁線圈中的電流進行控制，繼而產生可控阻力。開關管為MOS－FET，原理見圖4。

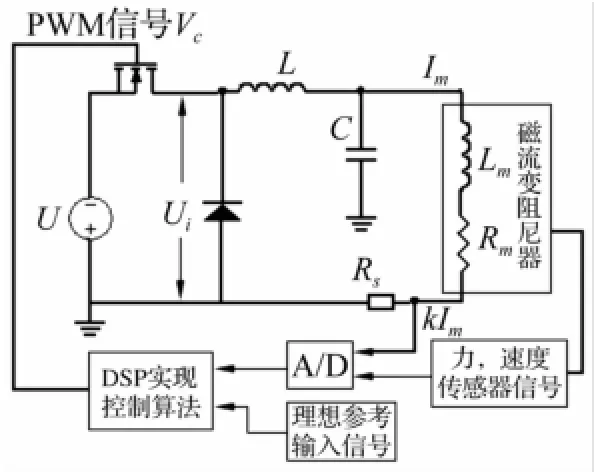
圖4 電磁回路原理圖Fig．4 The schematic diagram of electromagnetic driver circuit

電路達穩態時阻尼器勵磁線圈中電流大小與PWM信號的占空比D成正比例關系，即Im＝DU／R。其中U為電源電壓。該電路響應時間為毫秒級較短，在對響應時間無苛刻要求的控制系統中可忽略不計，簡化為比例環節。但因沖擊后坐過程僅幾百毫秒，故該電路動態響應時間可能對控制效果產生重要影響，不可忽略［13］。該電路以控制電壓Vc（獲得一定占空比D的PWM信號）為控制輸入，線圈電流Im為輸出，電磁電路為三階系統，其響應時間與磁流變阻尼器負載鐵芯線圈電阻及電感大小有關［14］，即

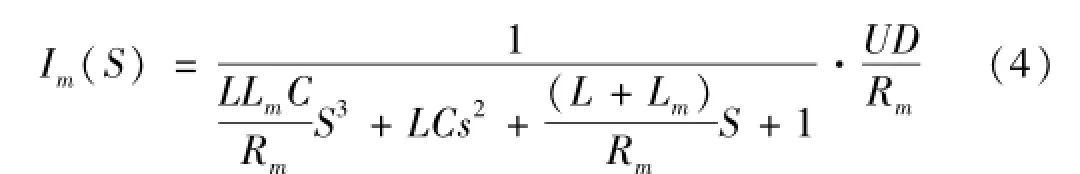
式中：D＝5V／Vc為PWM信號的占空比，對電路分別施加階躍電壓控制信號Vc＝1．60 V、2．66 V、3．75 V、5．00 V，對應電流Im的穩態值為0．5 A、1 A、1．5 A、2 A。通過電阻Rs對線圈電流進行采樣，觀察線圈電流信號Im的響應。

為方便信號比較對Vc進行歸一化處理，使其值與電流穩態值相等，記為見圖5。由于帶鐵芯線圈的非線性電感作用，對不同輸入值Vc系統參數在一定范圍內變化，電流響應時間分別為40 ms（0．5 A時），30 ms（1 A時），40 ms（1．5 A時），65 ms（2 A時）不等。且超調量較大。因響應時間較長，難以滿足幾百毫秒后坐控制要求。因此設計中應考慮對電磁驅動電路進行PI校正，加快電流響應時間。

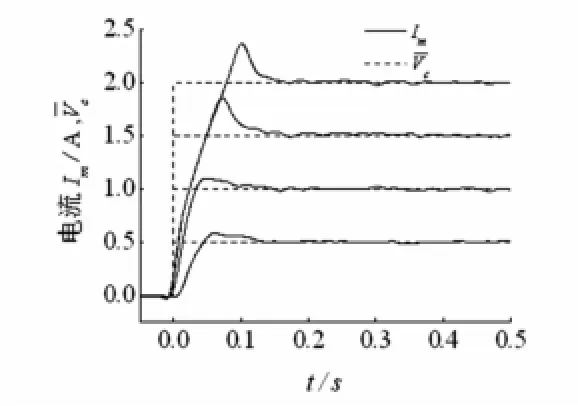
圖5 電磁驅動電路電流響應Fig．5 Current response of the electromagnetic driver circuit

2.2 磁流變阻尼器阻尼力響應時間測定

測試阻尼器輸出阻力及電流Im對Vc的階躍響應。火藥量4．0 g后坐開始50 ms處對阻尼器施加階躍電壓輸入信號Vc分別為1．6 V、2．66 V、3．75 V、5．00 V，對應電流穩態值0．5 A、1 A、1．5 A、2．0 A。Vc＝2．66 V，Im＝1 A的試驗結果見圖6。因磁流變輸出阻力中僅庫倫阻力Fτ受工作電流控制，其粘性力僅與后坐速度vr有關，故本文定義磁流變阻尼器輸出阻力響應時間為庫侖阻尼力Fτ對工作電流Im的響應時間。由圖6（b）中無法觀察到阻尼器輸出阻力中Fτ的響應時間，此因隨后坐速度變化的粘性阻力Fη存在。利用阻尼力模型（式（3））去除隨速度變化的粘性阻力，間接獲得Fτ，即

Fτ曲線見圖6（c）。為比較Fτ與電流Im的響應時間，將Fτ及Vr歸一化處理，使其最大值相同，記為＝ Fτ／3 300。由圖6（c）可觀察到Fτ的響應略慢于線圈電流響應，存在短暫延遲，庫倫阻尼力相對電流延遲時間（即磁流變液材料響應時間）約8 ms。

由以上分析知，磁流變阻尼器阻尼力響應時間受線圈電磁回路電流響應影響較大，可視為三階線性系統；而磁流變液材料響應時間可視為延遲單元［13－14］。與電流響應相比，磁流變液材料延遲時間較短且難以調節，因此在磁流變后坐控制系統設計時應對電磁回路進行校正，加快電流響應，提高阻尼器輸出阻力響應時間，獲得快速跟蹤性能。

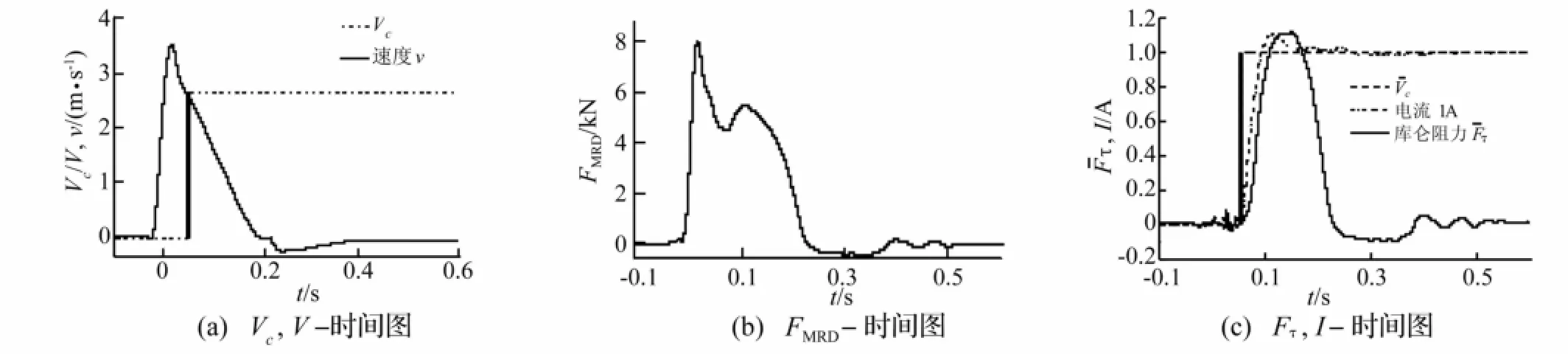
圖6 Vc＝2．66 V時磁流變阻尼器響應Fig．6 Response time of MR damper at Vc＝2．66 V

3 磁流變沖擊后坐控制系統研究

3.1 磁流變后坐阻尼控制系統總體方案設計

為獲得理想的后坐動態特性，應使后坐阻力FR為常數。由于磁流變阻尼器阻尼力構成中僅Fτ受電流控制，而粘性力Fη由后坐速度vr決定不受電流控制，因此磁流變后坐控制系統為：以線圈電流驅動電路控制電壓Vc為控制量，可調庫侖阻力Fτ為輸出，要求Fτ（t）能快速準確跟蹤理想參考庫倫阻力曲線Fτr（t），從而獲得理想后坐阻力。應離線獲得理想庫侖阻力曲線Fτr。設理想后坐阻力FRr＝常數（圖1），由式（1）在matlab下仿真理想后坐過程，獲得其速度軌線vrr，再由式（5）得Fτr。

控制區域應在后坐速度峰值后開始（0．03 s處），3．2 g藥量下仿真所得Fτr曲線見圖7。由圖7看出，Fτr逐漸上升以補償粘性阻力下降。

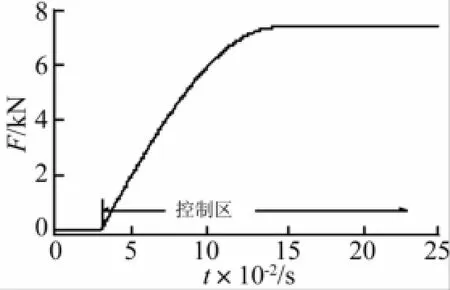
圖7 理想庫倫阻力Fτr曲線及控制區域Fig．7 Ideal curve of Fτrand determination of the control region

控制系統由控制電壓Vc獲得庫侖阻力Fτ，本身即構成穩定的閉環。為使Fτ能更快速準確跟蹤理想曲線，并具有抗干擾能力，本文據閉環反饋思想，擬定雙閉環反饋回路對其進行校正，磁流變沖擊后坐控制系統方案見圖8，具體①內環對阻尼器線圈電磁回路電流進行PI校正，提高電流響應時間；②外環對輸出可調庫侖阻力Fτ進行誤差反饋，消除阻尼力模型誤差，提高系統抗干擾性。該控制系統數學模型明確，且控制時間較短，應選快速簡潔的PI校正控制。

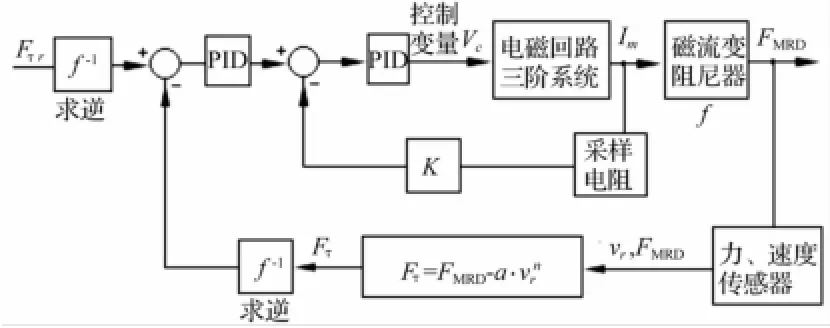
圖8 控制系統方案圖Fig．8 Scheme of the recoil control system

方案說明：①Fτ反饋計算中考慮實際后坐速度，故該控制系統對后坐過程速度波動及阻力波動均具有抗干擾性。由線圈電流產生的庫倫阻力Fτ為非線性環節f，應先用逆系統原理進行反饋線性化，通過取逆Im＝f－1（Fτ）消除非線性環節，再利用線性反饋PI控制算法。②電流與庫倫阻力非線性關系f－1由動態特性試驗測得。為保證運算快速，避免（圖8）Fτ指數運算及f－1，在程序中用表格方式實現。

3.2 試驗結果

控制系統實現原理見圖4。采用dspace硬件在回路系統實現快速原型。試驗用3．2 g及4 g兩種藥量進行測試。對每種藥量沖擊試驗分別采用固定參考曲線Fτr無反饋及雙閉環反饋跟蹤控制方案。

3．2 g藥量試驗結果見圖9。由圖9（b）看出，速度峰值接近，沖擊能量相近。后坐時間170 ms時兩次后坐位移相近，見圖9（a）。由圖9（c）、（d）看出，兩種控制方法對后坐阻力FR均產生有效控制，而反饋控制曲線更平坦。其速度峰值處兩條阻力曲線均出現局部峰值，大小相近。無反饋時速度峰值過后出現明顯凹陷（最低點6 417 N），而末端出現凸起峰值（最高點7 501 N），浮動1 084 N；反饋控制曲線相對平坦，阻力峰值出現在速度峰值處，為7 255 N，最小值為7 013 N，僅浮動242 N。后坐位移相同情況下反饋控制較無反饋時阻力峰值減小246 N，后坐特性更理想。其改善原因可由電流Im及Fτ響應時間說明，見圖9（e）、（f）、（g）。其中歸一化處理后曲線擾動因后坐速度傳感器信號波動所致。由圖9（e）看出，反饋控制電流響應時間明顯加快，能快速跟蹤理想電流曲線。比較圖9（f）、（g），無反饋及反饋控制下，電流Im到終值2 A的時間分別為114 ms、84 ms，Fτ到終值時間分別為121 ms、89 ms。在38 ms處（對應圖9（c）無反饋曲線凹陷處），反饋控制Fτ已達1 677 N，無反饋控制Fτ僅854 N。無反饋控制時（圖9（f）），由于Im、Fτ未及時響應，使后坐阻力在38ms處出現凹陷。反饋控制（圖9（g））電流Im、Fτ的響應明顯加快，使后坐阻力能快速補償粘性力的下降，未出現明顯凹陷。

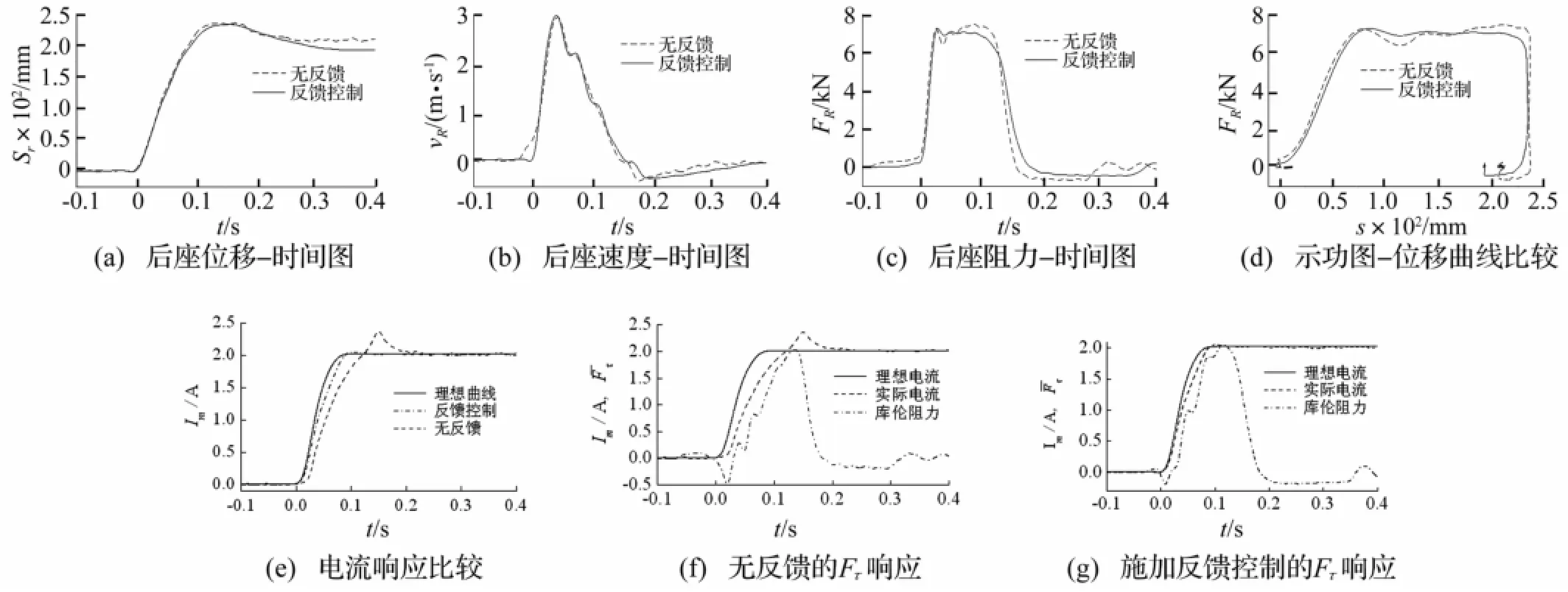
圖9 3 g藥量后坐控制比較圖Fig．9 Curves of MR recoil damper with 3 g powders

4 g藥量試驗結果見圖10。由圖10（b）看出速度峰值相等，且圖10（d）中兩曲線包圍面積近似相等，故兩次沖擊能量相近。比較圖10（c）、（d），反饋控制能明顯補充無反饋時阻尼力產生的凹陷，充滿度更好，顯著減小后坐位移（圖10（a）），即由300 mm降到270 mm。沖擊藥量增大后，反饋控制對提高阻尼器響應時間效果更顯著，見圖10（e）、（f）、（g）。然而亦有不足之處，即兩條阻力曲線均為下降趨勢（圖10（c）），未達理想水平線。其原因為4 g藥量沖擊載荷增大，后坐速度峰值增大，導致粘性阻力峰值增大，粘性阻力峰值（對應速度峰值處）達9 280 N。而庫倫阻力Fτ最大只能達7 300 N，后坐臨近結束時速度趨近零，粘性阻力降為零，剩余的庫倫阻力7 300 N無法使總阻尼力保持水平。

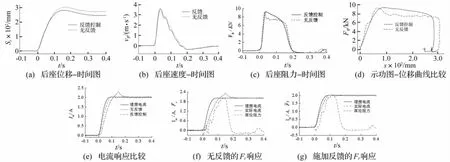
圖10 4 g藥量后坐控制比較圖Fig．10 Curves of MR recoil damperwith 4 g powders

庫倫阻力與粘性阻力最大值的比值稱為可調系數，決定磁流變阻尼器阻尼力的可控范圍。該值由阻尼器結構設計決定。試驗結果表明，結構設計中若可調系數達不到，則無論施加何種控制方法也無法獲得飽滿的后坐阻力充滿度。因此，可調系數作為重要幾何特性參數在進行磁流變阻尼器結構設計中應足夠大。

4 結 論

兩種藥量的沖擊試驗充分驗證了磁流變沖擊后坐控制系統響應時間對后坐動態特性的重要性。試驗結果總結如下：

（1）磁流變阻尼器響應時間受電磁電路電流響應影響較大，影響輸出阻力的跟蹤性能。用理想軌跡跟蹤控制方案及PID雙閉環反饋控制算法可有效加快后坐阻力動態響應，使充滿度飽滿，可獲得良好的后坐動態特性。

（2）4 g藥量試驗用反饋控制雖可加快后坐阻力動態響應，但充滿度不夠。由于磁流變阻尼器可調阻力相對粘性力不足，設計時應保證足夠大的可調系數，以增大阻尼力可控范圍，以使大藥量時亦能獲得飽滿的充滿度。

［1］Ahmadian M，Poynor J C．An evaluationg of magneto rheological dampers for controlling gun recoil dynamics［J］．Shock and Vibration，2001，8（3）：147－155．

［2］Ahmadian M，Appleton R，James A．An analytical study of fire out of battery using magneto theological dampers［J］．Shock and Vibration，2002，9：129－142．

［3］周淵，張永亮，劉軍，等．一種剪切式磁流變車削減振器的設計與減振試驗［J］．振動與沖擊，2013，32（4）：167－172．

ZHOU Yuan，ZHANG Yong-liang，LIU Jun，et al．Design and test of a sheartype MR damper for turning vibration suppression［J］．Journal of Vibration and Shock，2013，32（4）：167－172．

［4］祝長生．盤型磁流變流體阻尼器懸臂轉子系統響應時間測試［J］．航空動力學報，2006，21（3）：550－555．

ZHU Chang-sheng．Response time measurement of a cantilever rotor with a disk-type Magnetorheological fluid damper［J］．Journal of Aerospace Power，2006，21（3）：550－555．

［5］郭鵬飛，關新春，歐進萍．磁流變液阻尼器響應時間的實驗研究及其動態磁場有限元分析［J］．振動與沖擊，2009，28（6）：1－5．

GUO Peng-fei，GUAN Xin-chun，OU Jin-ping．Experimental study and dynamic magnetic finite element analysis on the response time of Magnetorheological fluid dampers［J］．Journal of Vibration and Shock．，2009，28（6）：1－5．

［6］董小閔，丁飛耀，管治，等．面向高速的磁流變緩沖器多目標優化設計及性能研究［J］．機械工程學報，2014，5：1－8．

DONG Xiao-min，DING Fei-yao，GUAN Zhi，et al．Multiobjective optimization and performance research of magnetorheological absorber under high speed［J］．Chinese Journalof Mechanical Engineering，2014，5：1－8．

［7］李趙春，王炅．基于磁流變阻尼器的沖擊緩沖系統控制方法［J］．南京理工大學學報，2012，36（4）：656－661．

LI Zhao-chun，WANG Jiong．Control methods for shock isolationg system using Magnetotheological fluid damper［J］．Journal of Nanjing University of Science and Technology，2012，36（4）：656－661．

［8］Hu Hong-sheng，Jiang Xue-zheng，Wang Jiong，et al．Design，modeling，and controlling of a large-scalemagnetorheological shock absorber under high impact load［J］．Journal of Intelligent Material Systems and Structures，2012，23（6）：635－645．

［9］Li Zhao-chun，Wang Jiong．A gun recoil system employing a magnetorheological fluid damper［J］．Smart Materials and Structures，2012，21（10）：105003．

［10］高樹滋．火炮反后坐裝置設計［M］．北京：兵器工業出版社，1995：71－79．

［11］張莉潔，王炅．沖擊載荷下磁流變阻尼器動態特性分析及模型參數辨識［J］．機械工程學報，2009，45（1）：211－217．

ZHANG Li-jie，WANG Jiong．Dynamic performance analysis and model parameter identifications of mr dampers under impact load［J］．Chinese Journal of Mechnical Engineering，2009，45（1）：211－217．

［12］Wang X J，Gordaninejad F．Study of field-controllable，electro-and magneto-rheological fluid dampers in flow mode using herschel-bulkley theory［J］．Smart Structures and Materials 2000：Damping and Isolation，Proceeding of SPIE，2000，3989：232－243．

［13］Koo J H，Fernando D．Goncalves．Investigation of the respose time of magnetorheological fluid dampers［J］．Damping and Isolation，Proc．of SPIE，2004，5386：63－71．

［14］Yang G，Spencer Jr B F．Large scale MR fluid dampers：modeling and dynamic performance considerations［J］．Engineering Structures，2002，24：309－323．

Experiments on magneto-rheological recoil control system

ZHANG Li-jie1，CHANG Jia-dong1，WANG Jiong2，CHENGGuang-wei1
（1．Dept．of Mechanical Engineering，Luoyang Institute of Science and Technology，Luoyang471023，China；2．School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，China）

Since the critical demand for time response of MR damper in gun recoil buffering applications，experimental studies on MR recoil control system were carried out on an impact test rig with the special designed MR damper．The impact performance of the MR damper described by a physical model under fixed operating current was obtained．The time responses of the MR damper's coil current and the damping force were respectively tested，then a trajectory tracking control scheme for MR recoil system was put forward，so that the adjustable damping force of MR can accurately track an ideal reference curve．Experimental results with 3g and 4g powders under the double close-looped feedback control aswell as the fixed damping curve controlwithout feedback were obtained．By comparisons，it is shown that the feedback control can efficiently reduce the response time of the damping force and provide more rapid tracking ability．With the same displacement，smaller peak of recoil force is produced，while with the same peak of recoil force，more less displacement is achieved．Analyzing the decline of the damping force curve with 4g powders，it’s suggested the adjustable coefficient of the damping force，as an important parameter，must be large enough in MR dampers’structural design．

magneto-rheological damper；impact loading；recoil buffering；response time；trajectory tracking control

TH113．1

：A

10．13465／j．cnki．jvs．2014．22．021

國家自然科學基金資助項目（50675106）；國家自然科學基金（51175265）

2014－02－14 修改稿收到日期：2014－06－27

張莉潔女，博士，講師，1976年12月生