基于各向同性本構關系薄層單元的螺栓連接參數識別

姜 東，吳邵慶，史勤豐，費慶國

（1．東南大學工程力學系，南京 210096；2．江蘇省工程力學分析重點實驗室，南京 210096）

基于各向同性本構關系薄層單元的螺栓連接參數識別

姜 東1，2，吳邵慶1，2，史勤豐1，2，費慶國1，2

（1．東南大學工程力學系，南京 210096；2．江蘇省工程力學分析重點實驗室，南京 210096）

針對螺栓連接建模與參數識別問題開展研究。基于各向同性本構關系薄層單元理論，提出螺栓連接結構接觸面力學性能識別方法。對單個螺栓搭接及多個螺栓搭接兩種結構分別進行有限元建模，忽略螺栓質量、螺孔影響，搭接界面采用各向同性本構關系的薄層單元模擬。根據試驗模態參數構造優化問題，識別搭接界面薄層單元材料參數。結果表明，兩種螺栓連接結構前四階彎曲模態頻率計算精度較高，薄層單元能準確反映接觸界面力學性能。該方法適用于單個螺栓及螺栓較密集工況動力學精確模擬。

螺栓連接；各向同性；薄層單元；參數識別

機械結構中的螺栓等連接件會嚴重影響結構局部剛度及整體動力學性能。連接處動力學參數對建立準確的動力學模型起決定性作用，是準確計算結構動態特性與響應的前提。

螺栓連接結構有限元模擬方法主要分兩類，即非線性接觸算法與界面單元法［1－2］。前者需不斷通過接觸算法判別接觸狀態，迭代計算結構響應，計算量較大；而后者可在保證計算精度前提下降低計算量。彈簧單元、一般單元（Generic element）、零厚度單元（Zero thickness element）及薄層單元（Thin layer element）為較常用接觸界面力學性能參數化方法。Ren等［3］僅考慮接觸界面平動自由度，轉動自由度通過平動自由度實現。Ahmadian等［4］采用一般單元方法模擬螺栓連接搭接情況，通過試驗頻響函數識別單元參數；Mayer等［5］利用零厚度單元及薄層單元提出能有效模擬接觸面方法。薄層單元理論最早來自模擬巖石接觸力學分析［6－7］。已有研究將薄層單元成功用于焊接、螺栓連接等形式的機械連接建模［8－9］。金峰等［10］用薄層單元分析重力壩體的抗震穩定性；黃耀英等［11］分析基于橫觀各向同性體本構方程簡化獲得薄層單元本構方程。楊紅平等［12］基于分形幾何及接觸力學理論表征粗糙表面微凸體參數，提出機械結合面法向接觸剛度計算模型。田紅亮等［13］采用虛擬各向同性材料模擬固定連接界面，基于赫茲接觸理論與分形理論推導等效虛擬材料參數，有限元分析頻率與試驗值誤差小于9%。黃開放等［14］基于虛擬材料方法研究預緊力變化的連接結構動力學仿真，結果與試驗值誤差在±6%以內。

本文針對螺栓連接建模與參數識別問題在線性范圍內開展研究。基于薄層單元理論，對單、多螺栓搭接兩種結構進行有限元建模與參數識別。接觸界面采用基于各向同性本構關系的薄層單元模擬。進而提出基于薄層單元的螺栓連接結構接觸面力學性能模擬方法。

1 薄層單元基本理論

對于固定接觸界面的螺栓連接結構，結合面始終保持接觸，接觸狀態為粘附或者僅發生微小的局部相對位移（微觀滑移和微觀拍擊）。在該前提下，接觸面之間的作用力僅存在線性的法向接觸力與切向摩擦力。薄層單元能夠較準確的反映接觸面力學性能。

薄層單元最早由Desai等［6］提出并用于巖土結構接觸分析，在相鄰接觸體間定義一層單元等效模擬連接界面接觸力學特征。考慮尺寸l1×l2×d薄層單元，據虛位移原理得虛功方程為

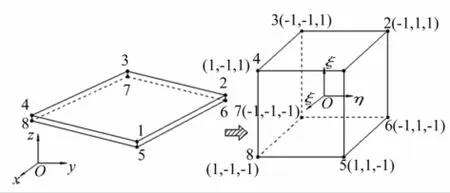
圖1 薄層單元等參變換Fig．1 Isoparametric transformation of thin-layer element

對薄層單元，設厚度d遠小于另兩方向特征尺寸l1，l2。研究表明［6］，單元面內應變分量（εx，εy，γxy）、應力分量（σx，σy，τxy）會被忽略。用單元形函數［11］分析時則有?Ni／?z遠大于?Ni／?x及?Ni／?y（Ni為單元形函數），可認為?Ni／?x＝?Ni／?y≈0，從而得出應變分量εx＝εy＝γxy≈0。因此薄層單元在高斯點的應變分量有三個不為零，應變分量可簡化為ε＝［εzγyzγzx］T。若接觸面法向｛e｝n與兩切向｛e｝t分別定義為薄層單元局部坐標系z，x，y方向，據以上分析，設連接界面法向、切向接觸性能相互獨立，兩切向接觸性能具有一致性，表征界面接觸性能的薄層單元本構方程為

此時法向彈性常數與切向彈性常數為非獨立的。

2 薄層單元參數確定

2.1 單元厚度

薄層單元厚度選擇對計算結果影響較大。厚度過大則單元會有6個應變分量，難以準確體現接觸界面力學特征，不能用于模擬接觸情況；厚度過小則會導致雅可比矩陣行列式值趨向于零，致矩陣病態、求逆困難、無法計算位移－應變關系。對薄層單元建模單元厚度選擇定義比例系數［1，6－7］為

文獻［6］認為Ratio取值為10～100時能獲得較準確結果。

2.2 接觸剛度

接觸剛度的確定為基于薄層單元螺栓連接結構有限元模擬關鍵。接觸面保持線性粘合狀態時彈性矩陣中G，E均為常數［1］，需試驗獲得。通過測試接觸界面應力與位移間關系得到法向、切向接觸剛度［6］為

式中：kn為法向接觸剛度；kτ為切向接觸剛度；d為薄層厚度；ur，vr為薄層法向及切向位移；σ，τ為薄層法向及切向應力。

該方法雖基于混凝土接觸試驗，但對機械連接結構界面接觸問題亦具有一定參考意義。通過螺栓連接結構切向受力試驗獲得接觸面等效剪切模量與切向剛度之關系［15］為

式中：A為實際接觸面積；k為連接切向剛度，與接觸界面面壓及摩擦性能等有關，其值為試驗所得連接處切向力與切向位移關系曲線斜率。

以上兩種界面接觸剛度測試方法可獲得近似薄層單元彈性參數，將材料本構關系集成于薄層單元中能對連接結構進行準確有限元動力學分析。采用該方法對不同方向接觸剛度需分別進行試驗；對試驗裝置、試驗方法要求較高。本文采用動態試驗數據識別螺栓連接結構結合面薄層單元參數。

3 算例研究

分別對單個螺栓及多個螺栓搭接結構開展研究。結構Ⅰ由一個螺栓與兩塊鋁板搭接；結構Ⅱ由兩塊鋁板通過4個螺栓搭接。螺栓型號均為M10。結構幾何尺寸及搭接見圖2、圖3，搭接板材料參數見表1。

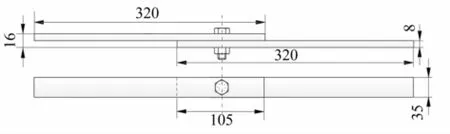
圖2 螺栓搭接結構Ⅰ（單位：mm）Fig．2 Bolted joint structureⅠ

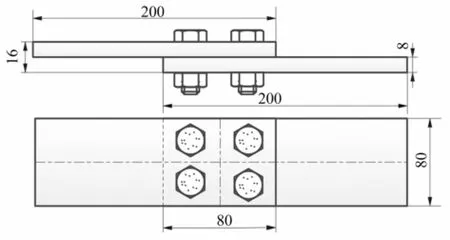
圖3 螺栓搭接結構Ⅱ（單位：mm）Fig．3 Bolted joint structureⅡ

表1 搭接板材料參數Tab.1 Material properties of the lapp ing p late

3.1 模態試驗結果

對兩種螺栓搭接模型分別進行模態試驗。螺栓預緊力對連接結構動態特性有較大影響，預緊力大到一定程度時結構固有頻率不會隨預緊力的增加而變化。用錘擊法以螺栓搭接結構Ⅱ為例進行模態試驗說明，測試與測點布置見圖4、圖5。采用彈簧繩懸掛方法模擬自由－自由邊界條件，傳感器布置于結構端部以避開振型節點；為獲得較光滑振型曲線共布置13個測點。螺栓搭接結構Ⅰ的試驗條件與此類似。通過試驗得螺栓搭接結構Ⅰ，Ⅱ前四階試驗模態數據見圖6。

圖4 螺栓搭接結構Ⅱ測試情況Fig．4 The experiment condition of bolted structureⅡ

圖5 測點布置Fig．5 Test point arrangement

圖6 螺栓搭接結構Ⅰ，Ⅱ前四階試驗模態數據Fig．6 The first four experimentalmode shapes and modal frequencies of bolted structureⅠandⅡ

3.2 薄層單元參數識別

本文對模型Ⅰ，Ⅱ建立有限元模型，忽略螺栓質量及螺孔影響，搭接板用實體單元模擬，界面用各向同性薄層單元模擬。將薄層單元材料參數識別轉化為優化問題。待識別參數為接觸面薄層單元材料彈性模量E與剪切模量G。建立目標函數為前四階彎曲振型計算、試驗結果殘差加權平方和最小，即

式中：J（p）為目標函數定義在結構待識別參數合理取值范圍p1≤p≤p2內，試驗與計算模態參數殘差加權平方和取極小值；ε為模態參數殘差；zm，za（p）分別為試驗與計算的模態參數；W為反映各模態參數殘差相對權重的對角陣。

設定待修正參數初值，用靈敏度分析法迭代求解式（14）。第j個迭代步問題可描述為

式中：Sj＝W1／2?zj／?pj為模態參數對待修正參數的加權靈敏度矩陣。迭代直到待識別參數p收斂。計算模態參數精度滿足要求時可得準確的接觸面材料參數。

3．2．1 螺栓搭接結構Ⅰ

螺栓搭接結構Ⅰ結合面薄層單元示意圖見圖7。由于靠近螺栓部位接觸剛度高于遠離螺栓部位，將接觸面薄層單元等分為三部分，采用兩種不同的各向同性本構關系模擬及參數識別。靠近螺栓（圖中深色）區域待識別參數為彈性模量E1與剪切模量G1；遠離螺栓（圖中淺色）區域待識別參數為彈性模量E2及剪切模量G2。薄層比例系數Ratio＝10，材料密度為0。

圖7 螺栓搭接結構Ⅰ結合面薄層單元示意圖Fig．7 Thin-layer element in the contact surface of bolted structureⅠ

圖8為螺栓搭接結構Ⅰ結合面薄層單元材料參數迭代收斂曲線，表2為薄層單元材料參數初始值與識別值，表3為參數識別前后計算與試驗模態參數誤差比較。由識別結果看出，固有頻率最大誤差不超過1．0%，識別精度較高。表2中楊氏模量E大于剪切模量G，能反映接觸界面法向剛度大于切向接觸剛度特征；靠近螺栓區域結合面材料參數識別結果均遠大于遠離螺栓區域，能較好反映實際情況。因此基于各向同性材料的薄層單元能準確反映結合面切向、法向接觸性能，計算模態參數精度高。

表2 結合面薄層單元材料參數初始值和識別值Tab.2 The initial and the identified material parameters of the thin-layer element

表3 參數識別前后計算與試驗模態參數誤差比較Tab.3 Com parison betw een the com putational and experimental modal data before and after parameter identification

3．2．2 螺栓搭接結構Ⅱ

螺栓搭接結構Ⅱ由兩塊鋁板通過4個螺栓搭接而成。接觸界面螺栓分布更密集，與結構Ⅰ相比結構Ⅱ的接觸情況更復雜。由于螺栓預緊力產生的接觸面面壓分布非均勻，且4個螺栓距離較近，導致接觸剛度分布不均勻。結構Ⅱ在接觸界面定義兩種材料，在約兩倍螺桿直徑的矩形區域內定義各向同性材料1，待識別參數為彈性模量E1及剪切模量G1，其它區域定義各向同性材料2，識別參數為彈性模量E2及剪切模量G2。參數設置方法與結構Ⅰ相同。

圖9為螺栓搭接結構Ⅱ結合面等效材料參數迭代收斂曲線，表4為結合面薄層單元材料參數初始值與識別值，表5為參數識別前后計算與試驗模態參數誤差比較。由識別結果看出，計算模態頻率最大誤差不超過2．5%，識別精度較高；薄層單元材料彈性參數在螺栓附近明顯高于其它區域，且法向彈性模量大于剪切模量，與實際搭接結構接觸面接觸性能一致。因此基于各向同性材料的薄層單元能較好模擬多個螺栓搭接結構的連接性能。

圖8 螺栓搭接結構Ⅰ結合面薄層單元材料參數迭代收斂曲線Fig．8 Material parameter convergence of the thin-layer element in the contact surface of bolted structureⅠ

圖9 螺栓搭接結構Ⅱ結合面薄層單元材料參數迭代收斂曲線Fig．9 Parameter convergence of the thin-layer element in the contact surface of bolted structureⅡ

表4 結合面薄層單元材料參數初始值和識別值Tab.4 The initial and the identified material parameters of the thin-layer element

表5 參數識別前后計算與試驗模態參數誤差比較Tab.5 Com parison betw een the com putational and experimental modal data before and after param eter identification

4 結 論

（1）本文在各向同性本構關系薄層單元理論基礎上提出螺栓連接結構接觸面力學性能識別方法。通過固定結合面單、多個螺栓搭接兩種結構對方法進行驗證。

（2）采用線性各向同性本構關系薄層單元模擬接觸面，所提方法建模與參數識別效率較高，識別后參數能準確反映螺栓搭接結構結合面接觸性能。近螺栓區域接觸面材料參數識別結果大于遠離螺栓區域，能較好反映接觸界面剛度分布不均勻性。

（3）該方法能準確描述螺栓搭接結構接觸面力學性能，適用于單、多個螺栓搭接等多種工況有限元精確模擬。

［1］Bograd S，Reuss P，Schmidt A，et al．Modeling the dynamics of mechanical joints［J］．Mechanical Systems and Signal Processing，2011，25：2801－2826．

［2］Mackerle J．Finite element analysis of fastening and joining：a bibliography（1990－2002）［J］．International Journal of Pressure Vessels and Piping，2003，80（4）：253－271．

［3］Ren Y，Beards C F．Identification of effective linear joints using coupling and joint identification techniques［J］．Journal of Vibration and Acoustics，1998，120（2）：331－338．

［4］Ahmadian H，Jalali H．Generic element formulation for modelling bolted lap joints［J］．Mechanical Systems and Signal Processing，2007，21：2318－2334．

［5］Mayer M，Gaul L．Segment-to-segment contact elements for modeling joint interfaces in finite element analysis［J］．Mechanical Systems and Signal Processing，2007，21：724－734．

［6］Desai C S，Zaman MM，Lightner J G，et al．Thin-layer element for interfaces and joints［J］．International Journal for Numerical and Analytical Methods in Geomechanics，1984，8（1）：19－43．

［7］Sharma K，Desai C．Analysis and implementation of thinlayer element for interfaces and joints［J］．Journal of Engineering Mechanics，1992，118（12）：2442－2462．

［8］Ahmadian H，Jalali H．Identification of bolted lap joints parameters in assembled structures［J］．Mechanical Systems and Signal Processing，2007，21：1041－1050．

［9］Jalali H，Hedayati A，Ahmadian H．Modeling mechanical interfaces experiencingmicro-slip／slap［J］．Inverse Problems in Science and Engineering，2011，19（6）：751－764．

［10］金峰，邵偉，張立翔，等．模擬軟弱夾層動力特性的薄層單元及其工程應用［J］．工程力學，2002，19（2）：36－40．

JIN Feng，SHAOWei，ZHANG Li-xiang，et al．A thin-layer element for simulation of static and dynamic characteristics of soft interlayer and its application［J］．Engineering Mechanics，2002，19（2）：36－40．

［11］黃耀英，吳中如，王德信．薄層單元基本假設和簡化探討［J］．力學與實踐，2008，130（2）：49－52．

HUANG Yao-ying，WU Zhong-ru，WANG De-xin．Discuss on fundamental assumption and simplification of thin-layer element［J］．Mechanics in Engineering，2008，130（2）：49－52．

［12］楊紅平，傅衛平，王雯，等．基于分形幾何與接觸力學理論的結合面法向接觸剛度計算模型［J］．機械工程學報，2013，49（1）：102－107．

YANG Hong-ping，FU Wei-ping，WANG Wen，et al．Calculation model of the normal contact stiffness of joints based on the fractal geometry and contact theory［J］．Journal of Mechanical Engineering，2013，49（1）：102－107．

［13］Tian Hong-liang，Li Bin，Liu Hong-qi，et al．A new method of virtual material hypothesis-based dynamic modeling on fixed joint interface in machine tools［J］．International Journal of Machine Tools＆Manufacture，2011，51：239－249．

［14］黃開放，金建新．基于虛擬材料方法的螺栓預緊力模擬的研究［J］．機械設計與制造，2012（8）：148－150．

HUANG Kai-fang，JIN Jian-xin．Research on bolt preload simulation based on virtual material method［J］．Machine Design＆Manufacture，2012（8）：148－150．

［15］Schmidt A，Bograd S，Gaul L．Measurement of join patch properties and their integration into finite-element calculations of assembled structures［J］．Shock and Vibration，2012，19（5）：1125－1133．

Parameter identification of bolted-joint based on themodelwith thin-layer elements with isotropic constitutive relationship

JIANG Dong1，2，WU Shao-qing1，2，SHIQin-feng1，2，FEIQing-guo1，2
（1．Department of Engineering Mechanics，Southeast University，Nanjing 210096，China；2．Jiangsu Key Laboratory of Engineering Mechanics，Nanjing 210096，China）

The finite elementmodeling and parameter identification of bolted jointswere concerned．According to the basic theory of thin-layer element with isotropic constitutive relationship，a parameter identification method for recognizing the mechanical characteristics of contact surface in bolted structures was proposed．The finite element modelingmethods for single andmultiple bolted structureswere investigated respectively，ignoring the hole and themass of the bolt，and modeling the contact surface by using thin-layer elements．Experimentalmodal datawere used for identifying the constitutive parameters of thin-layer elementwith an optimization procedure．Applying the identified parameters in the finite element model，the maximum error between the computational and experimental modal frequencies was reduced reasonably．It is shown that thin layer elementwith identified parameters can be used for accurately simulating the normal and tangential stiffness of contact surface．The proposed approach is available for precisely simulating the single and multiple bolted structures．

bolted-joint connection；isotropic；thin-layer element；parameter identification

TU318

：A

10．13465／j．cnki．jvs．2014．22．007

國家自然科學基金（10902024）；教育部新世紀優秀人才支持計劃（NCET－11－0086）；江蘇省自然科學基金（BK2010397）；江蘇高校優勢學科建設工程資助項目（1105007001）

2013－07－08 修改稿收到日期：2013－08－16

姜東男，博士生，1985年12月生

費慶國男，教授，博士生導師，1977年生