非線性弓形彈簧的設(shè)計(jì)與仿真

侍紅巖

(內(nèi)蒙古民族大學(xué))

1.引言

弓形彈簧是一種特殊形式的彈簧，最初主要應(yīng)用于箭術(shù)【1】方面，工業(yè)上應(yīng)用的相對(duì)較少。它屬于一種介于板彈簧和片彈簧之間的彈簧，其潛在應(yīng)用領(lǐng)域很廣。目前主要的應(yīng)用還是在油井開采過(guò)程中，弓形彈簧套管扶正器【2】作為一種輔助工具使用，也可以作為壓縮彈簧【3】或是減震彈簧【4】使用。但就目前來(lái)看弓形彈簧的建模方法比較少見，已有的設(shè)計(jì)方法與弓形彈簧的實(shí)際性質(zhì)差距較大。對(duì)于弓形彈簧來(lái)說(shuō)對(duì)機(jī)械特性（彎曲形狀和變形力）進(jìn)行建模比較難，因?yàn)槠鋬?nèi)力、力矩和幾何形狀都是未知數(shù)，而且其間的關(guān)系不是很明確。而且該系統(tǒng)的唯一閉合解對(duì)研究人員來(lái)說(shuō)用處不大。

對(duì)弓形彈簧進(jìn)行機(jī)械分析比較難，因?yàn)槠鋷缀涡螤钆c內(nèi)力和力矩錯(cuò)綜復(fù)雜地結(jié)合在一起，而內(nèi)力與力矩的力學(xué)分析比較直觀，最難不過(guò)為二階單變量積分。但是，弓形彈簧的幾何形狀不能簡(jiǎn)化為單微分方程。現(xiàn)有文獻(xiàn)中很少有關(guān)于弓形彈簧幾何變形與力之間關(guān)系的描述。

采用標(biāo)準(zhǔn)力學(xué)分析技術(shù)進(jìn)行兼容性分析。設(shè)弓形彈簧的長(zhǎng)度為L(zhǎng)，弓形彈簧首尾之間的變形為D，將弓形彈簧彎曲進(jìn)行安裝。因?yàn)楣螐椈蓮澢蟮男螤罴炔皇菕佄锞€也不是圓弧。因此外力與變形之間是非線性的關(guān)系，對(duì)這種非線性關(guān)系的求解只能采用近似求解的方法。需要事先給定一些假設(shè)條件，首先我們假設(shè)弓形彈簧各段的材料性質(zhì)一致，其次假設(shè)受力過(guò)程中所施加的外力大小和方向已知，另外假設(shè)彎曲過(guò)程中弓形彈簧的中點(diǎn)位置沒有發(fā)生移動(dòng)，最后假設(shè)變形過(guò)程在安全系數(shù)范圍內(nèi)進(jìn)行。

2.弓形彈簧的設(shè)計(jì)與建模

弓形彈簧在工業(yè)上的應(yīng)用主要是作為支撐和控制變形位移量的工件。根據(jù)其在實(shí)際應(yīng)用中的受力情況，發(fā)現(xiàn)通常弓形彈簧的受力點(diǎn)有兩種。一種是外力作用在弓形彈簧的兩端，另一種是外力作用在弓形彈簧的對(duì)稱中點(diǎn)。不管是哪個(gè)位置作為受力點(diǎn)，弓形彈簧受力后都會(huì)出現(xiàn)長(zhǎng)度（端到端的直線距離）和寬度（中點(diǎn)的切線到兩端連線的垂線）方向的變化。通過(guò)控制這兩方向變化的大小就可以控制相應(yīng)所需的位移量，可以是某一個(gè)方向上的，也可以是兩個(gè)方向綜合作用下的。

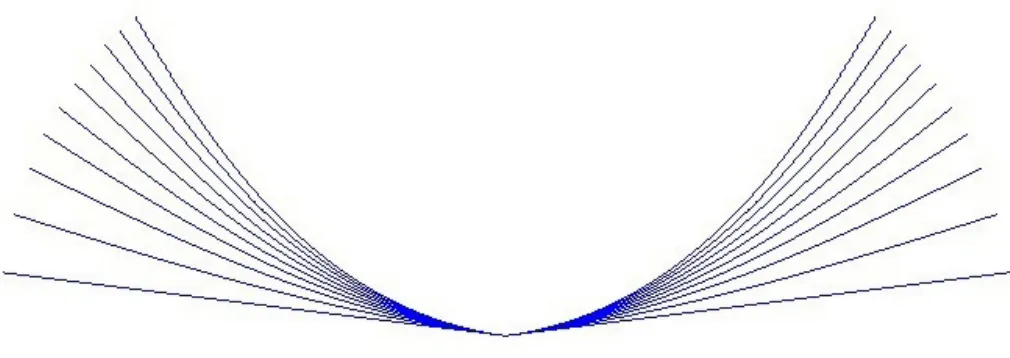
圖1 弓形彈簧受力變形過(guò)程

本文研究的受力點(diǎn)為在弓形彈簧兩端受大小相等的力。弓形彈簧為純彎曲薄片狀，厚長(zhǎng)比大于100。本文采用彎曲梁受力的分析過(guò)程來(lái)近似分析弓形彈簧的受力過(guò)程，為了便于分析，作出以下假設(shè)：材料為均勻的各向同性材料；變形過(guò)程中中點(diǎn)的位置不發(fā)生相對(duì)移動(dòng)；對(duì)稱部分的變形是同步的；弓形彈簧在手里變形時(shí)，其內(nèi)部應(yīng)變-應(yīng)力關(guān)系是線彈性的，并且彈性變形相對(duì)較小。

弓的內(nèi)力矩與二力軸的位移成正例【5】。顯而易見從弓的任何部分截取一段，在其上都有內(nèi)力矩M與Fy相等，F(xiàn)是端對(duì)端彈簧力，y是到載荷軸到中點(diǎn)的垂直距離。 為弓形彈簧一側(cè)的曲線段的切線（切點(diǎn)為弓形彈簧的末端）與水平線的夾角，定義為彎曲角。這個(gè)角度隨著弓形彈簧的受力會(huì)發(fā)生相應(yīng)的變化。因?yàn)閺椓Σ浑S切入的位置改變，發(fā)現(xiàn)。另外，根據(jù)曲率公式可知：

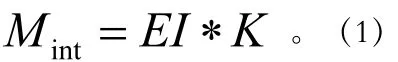
截取弓形彈簧上一個(gè)微小的片段，得：

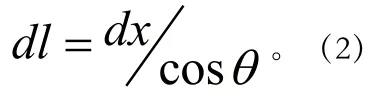
而曲率也可寫成：

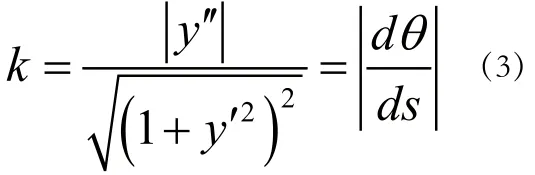
將公式（2）代入上式，得：

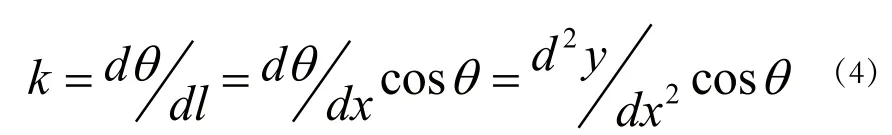
將公式（4）代入公式（1），得

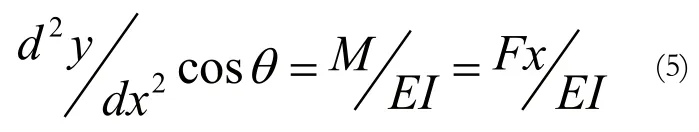
對(duì)公式（5）進(jìn)行兩次積分，得：

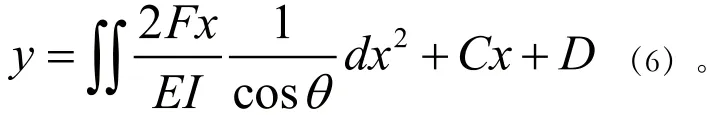
即：

假設(shè)弓形彈簧的中心對(duì)稱點(diǎn)在受力過(guò)程中沒有相對(duì)位移，則根據(jù)邊界條件：，得到，。那么公式（6）就可寫成：

上面這個(gè)公式表達(dá)了在假設(shè)條件下的弓形彈簧所受載荷與變形之間的關(guān)系。從中可以得到載荷與寬度變形、長(zhǎng)度變形以及長(zhǎng)寬綜合變形之間的關(guān)系。從這個(gè)公式中還可以看到，弓形彈簧的形狀會(huì)隨著載荷的變化而出現(xiàn)非線性的變化。

3.弓形彈簧的仿真模擬

由于弓形彈簧力與變形之間存在這非線性的關(guān)系，而且在公式中存在著四個(gè)未知量，所以用一般的數(shù)值算法很難進(jìn)行精確求解。為了得到弓形彈簧變形與受力之間的關(guān)系，本文采用MATLAB編程語(yǔ)言對(duì)弓形彈簧進(jìn)行建模【6】，運(yùn)用迭代的方式計(jì)算弓形彈簧彎曲部分的力學(xué)特性。改變其中的某些參數(shù)就可以看出得到不同性能的弓形彈簧的機(jī)械性能，從而用來(lái)分析各個(gè)變量對(duì)于弓形彈簧的機(jī)械性能影響程度。對(duì)于弓形彈簧來(lái)說(shuō)，初始狀態(tài)對(duì)其力學(xué)性能的影響大小可以通過(guò)下面的曲線知道，

下面是四條力與變形的曲線，初始參數(shù)EI=78，L=1m，dmax=0.29m，四條曲線的初始彎曲角分別為KAngle=0.05，0.1，0.15，0.2弧度。從曲線圖中可以看出，每條曲線的在變形小于0.02m的情況下，其斜率會(huì)有很大的不同，但是在變形大于0.05m時(shí)逐漸趨于同樣的斜率值收斂。從中可以看出初始彎曲角對(duì)弓形彈簧的影響還是比較大的，當(dāng)初始彎曲角比較小的時(shí)候，弓形彈簧在外力作用下比較容易變形，而初始彎曲角比較大的時(shí)候，會(huì)比較難變形。但是，當(dāng)變形量達(dá)到一定值的時(shí)候，初始彎曲角的大小對(duì)變形的影響就可以忽略不計(jì)了。而在變形量為0.02m至0.05m之間時(shí)，不同初始變形角的弓形彈簧均出現(xiàn)了曲線斜率的突變。初始變形角越小，這種突變出現(xiàn)的越早，也就是說(shuō)所需的外力越大。在經(jīng)過(guò)這個(gè)突變后，變形量的大小與外力

之間逐漸趨于正比關(guān)系。

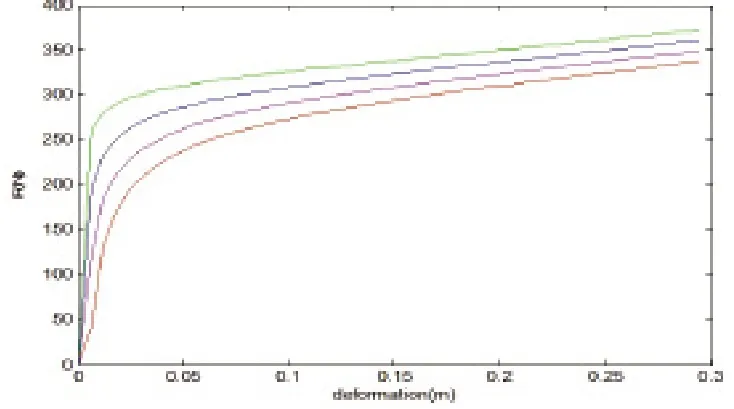
圖2 形變量與外力之間的模擬關(guān)系

4.試驗(yàn)結(jié)果對(duì)比分析

用彈簧鋼加工出一組長(zhǎng)度為1m，寬度為0.03m，厚度為0.005m，初始彎曲角為0.05弧度的弓形彈簧，在力學(xué)測(cè)試儀器上進(jìn)行力學(xué)性能對(duì)比測(cè)試。中點(diǎn)位置固定后，對(duì)兩端進(jìn)行加載，所加載荷為仿真實(shí)驗(yàn)所測(cè)得數(shù)據(jù)，可以得到相應(yīng)的實(shí)測(cè)變形量。將仿真變形量與實(shí)測(cè)變形量進(jìn)行對(duì)比，如表1。

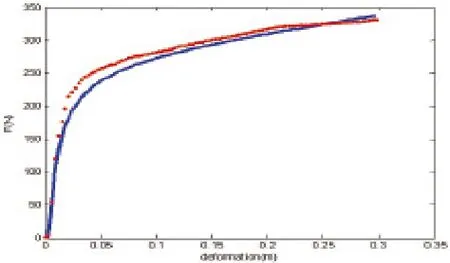
圖3 形變量與外力之間的實(shí)驗(yàn)關(guān)系

上圖中曲線代表仿真數(shù)據(jù)，點(diǎn)線代表實(shí)測(cè)數(shù)據(jù)，從中可以看到實(shí)測(cè)曲線與仿真曲線大致相同，兩者的差異相對(duì)來(lái)說(shuō)不是很大，最大的差異出現(xiàn)在變形量為0.03m，處，仿真值為193.1N,而實(shí)驗(yàn)值為217.5N，相對(duì)誤差達(dá)到了11%。這個(gè)最大誤差出現(xiàn)在弓形彈簧彈性的過(guò)渡期，也就是說(shuō)彈簧對(duì)變形的抵抗強(qiáng)度從強(qiáng)變?nèi)醯倪^(guò)渡期。經(jīng)過(guò)了這段線段后，誤差在逐漸減小，最小的誤差接近于0。

這個(gè)誤差變化產(chǎn)生的原因有幾個(gè)，其一是實(shí)驗(yàn)件加工中存在的誤差。其二是實(shí)驗(yàn)中測(cè)位移和力的準(zhǔn)確度不高。最主要的是因?yàn)樵诜抡娼Ｖ幸M(jìn)了假設(shè)的部分，并且對(duì)寬度沒有具體的限定。

5.結(jié)論

弓形彈簧并不是新型彈簧，只是對(duì)它的研究和應(yīng)用比較少，但這并不表明弓形彈簧沒有應(yīng)用價(jià)值。對(duì)一些跨度大，空間有限，變形量大的實(shí)際應(yīng)用方面還是有很大的使用前景。從上述模擬和實(shí)驗(yàn)的結(jié)果來(lái)看，可以采用避開弓形彈簧非線性變形的部分，利用它近視線性變形的部分進(jìn)行實(shí)際應(yīng)用，就可以合理有效地發(fā)揮其最大作用。目前急需對(duì)它進(jìn)行更全面和深入地研究。

【參考文獻(xiàn)】

1. Ihor Zanevsky。Compound archery bow asymmetry in the vertical plane[J]。Sports Eng ,2012 15:167-175

2.陳智等。一種弓形彈簧的設(shè)計(jì)與應(yīng)用[J]。石油機(jī)械，2010，38(8)，:71-73。

3. Dale A. Lawrenc。Bow Spring/Tendon Actuation for Low Cost Haptic Interfaces。First Joint Eurohaptics Conference and Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems , 2005:157-166。

4.凌榮江。汽車板簧的建模及非線性分析[D]。南京航天航空大學(xué)，碩士學(xué)位論文，2008。

5 付茂林。一類新的非線性動(dòng)力系統(tǒng)的穩(wěn)定性分析[J]。南華大學(xué)學(xué)報(bào)，2002，16（4）:15-17.6. 馬金奎.。基于MATLAB的彈簧優(yōu)化設(shè)計(jì)新方法[J]。機(jī)床與液壓，2004，12:99-101。