基于各向異性插值的全景圖像徑向展開算法

陶宏江，金龍旭

（中國科學院 長春光學精密機械與物理研究所，吉林 長春 130033）

1 引 言

折反射全景成像設備采用攝像機正上方放置折反射全景鏡頭達到擴大視野的目的，具有大視場、結構簡單、光能損失低、系統設計柔性好、無需運動部件掃描和搜索就可以實現實時360°成像等優點［1］。全景成像系統以及接近一個球面的全景視場信息觀察能力，在軍事和民用領域的應用前景都十分廣闊，目前已經在機器人導航、視頻會議、視頻監控、虛擬現實等眾多領域得到廣泛應用［2］。

然而，全景成像系統通過攝像機獲取的是圓形全景圖像，不符合人的視覺習慣，所以還需要對全景圖像進行展開，變成適合觀察分析的柱面全景圖像。

現在常用的展開算法依據場景中的物點坐標與成像平面內像點坐標映射關系實現圖像在展開［3］，但是由于展開的柱面圖像與全景圖像的像素點并不是一一對應關系，存在欠采樣現象，所以會產生圖像塊效應，降低展開圖像的圖像質量。本文分析了坐標映射展開法影響柱面圖像質量的原因，提出了結合各向異性插值的全景圖像徑向展開方法，該算法能夠有效的抑制塊效應、提高展開圖像質量。

2 基于坐標映射的柱面展開算法

2.1 坐標映射柱面展開算法的實現

基于坐標映射的柱面展開算法［4］的思想是，利用柱面展開圖中直角坐標和圓環狀全景圖極坐標之間的坐標變換，構建柱面圖中像素到圓環狀全景圖中像素的映射，再通過像素的填充完成柱面展開圖［5－6］，如圖1所示。

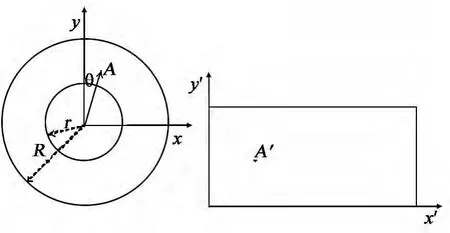
圖1 全景圖像展開示意圖Fig.1 Schematic forunwrapping panoramic images

圖1中，r表示圓環全景圖的內徑，R表示外徑，在外徑和內徑之間的區域為有效像素區。在圖像展開時，對于展開后柱狀圖中的任意一點A′（x′，y′），對應圓環全景圖中的點A（x，y），兩點間坐標關系可表示為

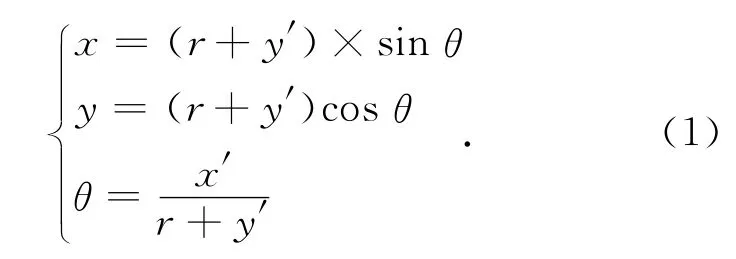
通過對柱面圖中每一點進行像素替換即可得到展開圖像。

2.2 坐標映射柱面展開算法的不足

由于計算機系統是一個離散的數字系統，這就導致了式（1）中的映射不是一個一對一的映射關系，即存在全景圖像中的一點對應柱面圖中多個點的情況。

不失一般性，假定圖像傳感器是正方式像素的陣列，全景相機成像時的示意圖如圖2所示。

圖2 全景相機成像示意圖Fig.2 Panoramic camera imaging

圖2中a表示傳感器一個像素單元的長度，Rm表示以o為原點的全景鏡頭光斑的半徑，可知沿A方向的傳感器感光像素數為個，而在B方向的傳感器感光像素數約為個，以為半徑的柱面展開圖有效像素近似分布如圖3所示［4］。

圖3 柱面展開圖有效像素近似分布Fig.3 Approximate distribution of the effective pixels of cylinder figure

通過分析可得出結論，在全景圖像的水平和垂直方向，柱面展開圖和全景圖像有一對一的映射關系，而在全景圖像的其他方向，展開圖像都有像素重復映射的情況，當方向角為π／2的整數倍時，像素重復映射最為嚴重，像素重復映射數近似為柱面展開圖中一列像素數的30%。

過多的像素重復映射是導致柱面展開圖像產生塊效應從而導致圖像質量下降的主要原因，而坐標映射柱面展開算法很難解決這一問題，因為它難以定位哪些像素是進行了多次映射的，針對這一問題，本文提出了全景圖像徑向展開算法。

3 全景圖像徑向展開算法

3.1 算法描述

全景圖像的徑向展開算法是基于數字圖像傳感器圖像采集原理和計算機圖形學算法的全景圖像展開方法，它的展開過程如圖4所示。

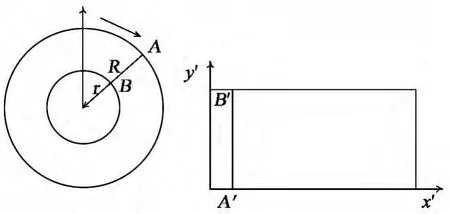
圖4 徑向展開過程Fig.4 Process of radial expanding

R是全景圖像外環半徑，r是全景圖像內環半徑，點A為全景圖像外環上的展開起點，B為全景圖像內環上的展開終點，A′為柱面展開圖中點A的對應點，B′為柱面展開圖中點B的對應點，線段A－B全景圖像自A 點起到B點結束的一條像素線段，線段A′－B′表示柱面展開圖中以A′點為基準的一列像素，徑向展開算法過程如下：

（1）首先使用Bresenham畫圓算法確定全景圖像外環在圖像中的像素位置，因為全景鏡頭和傳感器之間不會移動位置，所以這一過程只需要執行一遍；

（2）選擇展開的起點，本文選擇圓心位置正上方圓環外徑上的點，從起點開始，按順序以圓環外徑上的點執行步驟3中的直線掃描；

（3）從圓環外徑上的點開始，使用Bresenham直線算法沿半徑向圓心方向畫直線直到圓環內徑為止，把全景圖像中這條徑向上的點按順序對應到柱面如圖4中全景圖中的線段A－B對應到柱面展開圖中的A′－B′。

在僅使用Bresenham直線算法在全景圖像選擇線段復制到柱面展開圖中時，同樣會產生如圖3的像素缺失現象，本文使用基于Bresenham直線算法的線段拉伸算法以保證柱面展開圖中每一列具有同樣的像素數。

3.2 基于Bresenham直線算法的線段拉伸

Bresenham直線算法是計算機圖形學領域中使用最廣泛的直線掃描轉換算法，其具有只使用整數運算、只做加減法和乘2運算，實現方便，執行效率高的特點。

以第一象限為例，Bresenham直線算法以判斷誤差項d2－d1的符號來決定下一像素的取向，如圖5所示，當d2－d1＞0時，選擇右上方的點，否則選擇右側的點。

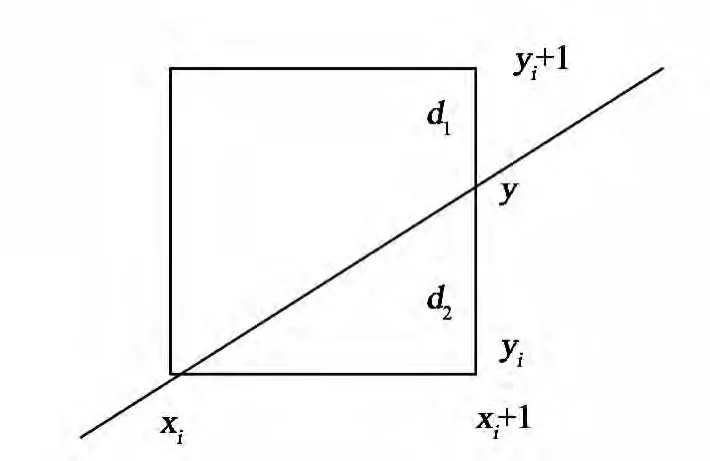
圖5 Bresenham直線算法簡述Fig.5 Bresenham straight－line algorithm outlined

結合圖2和圖3，可以得出結論：圖4中線段A－B拉伸所需要插入的像素個數與Bresenham直線算法向右上方選擇的次數有關，當直線每向右上方移動一點，就累積了槡2－1個像素的差異。

全景圖像的線段拉伸實現就是基于這一原理，以第一象限為例，算法過程如下：

（1）以Bresenham直線算法從全景圖像外環上的點向圓心畫直線，直到內環結束，計算直線上點的個數與全景圖像水平方向上R－r的差，即為圖像展開時需要插入的點的個數；

（2）重新執行Bresenham直線算法，在掃描過程中，當直線向右上方選擇時，對像素累積差異det加上槡2－1，如果直線向右選擇保持det不變；

（3）當累積像素差異det大于等于1時，如果已插入像素數大于等于第一步中計算出的總需要插入像素數，則不插入插值重構像素，否則即在柱面展開圖中對應位置增加一插值重構像素，同時det減1。

3.3 全景圖像的插值算法

全景圖像展開需要插入大量的插值像素，插入像素比例見圖3，像素插值的質量對柱面展開圖的視覺效果具有很大的影響，獲得高質量像素結果的主要手段就是濾除因圖像展開所帶來的圖像噪聲［6－8］，本文通過對全景圖像成像過程的分析，給出了基于各向異性插值［9－10］的全景圖像展開插值算法［11］，全景圖像成像過程如圖6所示。

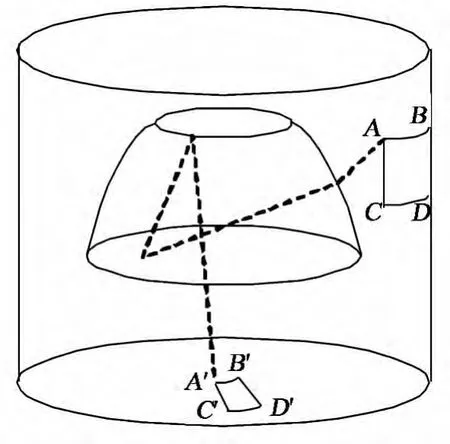
圖6 全景圖像成像過程Fig.6 Panorama image imaging process

上圖中圓柱為全景鏡頭的成像面，全景圖像的柱面展開也就是對全景鏡頭柱狀成像面數字化重構［6］，在柱狀成像面上有一待成像矩形區域AB－C－D，光線經過全景鏡頭雙曲面折射后再經過兩次反射在焦面上成像，成像面上的矩形A－B－CD 在焦面上成像為一段圓環A′－B′－C′－D′，成像面到焦面的平面映射示意圖如圖7所示。

圖7 成像面到焦面的平面映射示意圖Fig.7 Mapping schematic diagram of the image plane to the focal plane

通過上述分析可知，要在全景圖像的柱面展開圖中插值等效于在成像面中插值，也就是說成像面到焦面的映射等效于全景圖像的柱面展開到全景圖像的映射。

以焦面上全景圖像外圓環正上方點對應成像面的原點，成像面到焦面的映射關系為，成像面的x軸相當于焦面上全景圖像的外圓環方向，成像面的y軸相當于焦面上全景圖像的指向圓心的半徑。以第一象限為例，成像面上任一點M（mx，my），其在焦面極坐標上的位置為：

轉換為焦面直角坐標系中為：

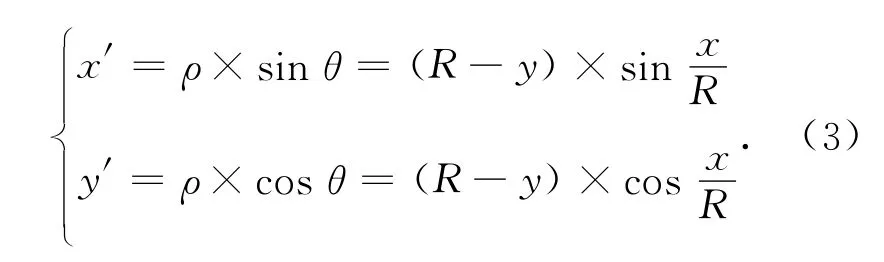
得出像素對應關系后，選擇高斯濾波器作為成像面上的插值濾波器［7］，濾波系數為：

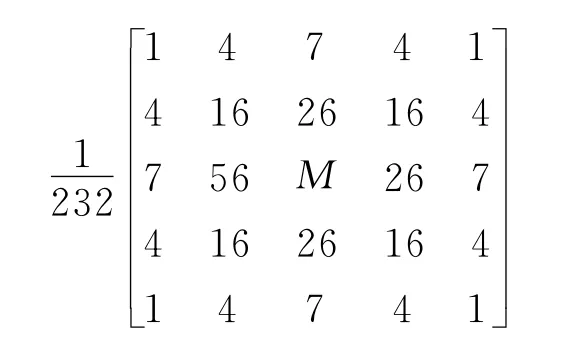
其中：M 為待插值點，坐標位置（mx，my），將以點M為中心的坐標系數矩陣通過成像面到焦面的映射關系映射到焦面上，這一映射過程是一個多對一的映射，焦面上映射后一個點上的濾波系數值是映射到這一點的所有成像面點的濾波系數值的和，構成由像面中極坐標位置決定的各方向系數不同的濾波數組［12］，最后通過映射后的各向異性濾波數組對待插值點進行求解得到插值結果。

4 實驗結果與討論

實驗系統使用2 048pixel×1 536pixel的CMOS傳感器作為圖像輸入源，使用本文算法對輸入圖像進行展開，輸入圖像和展開結果如圖8所示，展開圖像以輸入圖像正上方位置為起點，沿逆時針方向展開。由圖中可以看到在π／2的整數倍角度位置，圖像塊效應得到了改善，圖像質量得到了提高。本文算法和坐標映射展開算法的局部細節圖如圖9，相對坐標映射展開算法，本文算法結果在反光處集中度變高了，圖像質量獲得了改善。

圖8 實驗測試圖像和結果Fig.8 Image and result of experimental test

圖9 展開圖像細節Fig.9 Comparison of expanded image

對圖像的數值比較方法有很多種［13－16］，本文采用信息熵和平均梯度的方法比較圖像質量，如表1所示，結果表明本文算法除運行時間略低于坐標映射展開算法，在展開圖像包含的信息量和展開圖像邊緣輪廓清晰度方面都優于坐標映射展開算法。

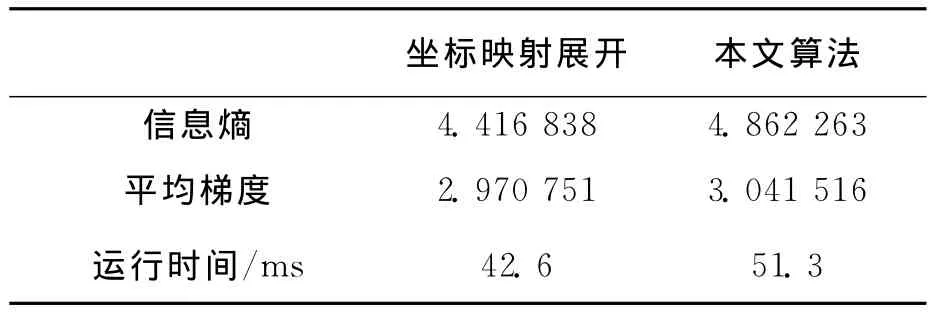
表1 實驗數據對比結果Tab.1 Comparison of experimental data

5 結 論

針對現有全景圖像展開算法適應性差，改進困難的矛盾，根據全景圖像成像原理結合計算機圖形學方法，提出了基于各向異性插值的全景圖形徑向展開算法。該算法具有靈活性強、實現簡單和執行效率較高等特點，實驗表明，該算法能夠改善全景圖像展開導致的塊效應，提高圖像質量。

［1］ 曾吉勇，蘇顯渝.折反射全景成像系統［J］.激光雜志，2004，25（6）：62－64.Zeng J Y，Su X Y.Catadioptric omnidirectional imaging system ［J］.Laser Journal，2004，25（6）：62－64.（in Chinese）

［2］ 原新，王亮，朱齊丹.基于全向視覺傳感器的圖像解算方法研究［J］.哈爾濱工業大學學報，2006，38（12）：2158－2161.Yuan X，Wang L，Zhu Q D.Image calculation research based on omni－directional camera［J］.Journal of Harbin Institute of technology，2006，38（12）：2158－2161.（in Chinese）

［3］ 陳旺，徐瑋，熊志輝，等.折反射全向圖像柱面展開校正算法研究［J］.中國圖像圖形學報，2009，14（12）：2559－2565.Chen W，Xu W，Xiong Z H，et al.Rectification of catadioptric omnidirectional images via cylindrical unwarping［J］.Journal of Image and Graphics，2009，14（12）：2559－2565.（in Chinese）

［4］ 田曉東.折反射全景成像系統分析與設計［J］.儀表技術與傳感器，2006（4）：48－50.Tian X D.Analysis and design of catadioptric panorama image system ［J］.Instrument Technique and Sensor，2006（4）：48－50.（in Chinese）

［5］ 何四華，邵曉方，楊紹清，等.雙曲面折反射全景成像柱面展開圖像質量分析［J］.激光與紅外，2012，42（2）：187－191.He S H，Shao X F，Yang S Q，et al.Analysis for the cylinder image quality of hyperbolic－catadioptric panorama image system ［J］.Laser ＆Infrared，2012，42（2）：187－191.（in Chinese）

［6］ 任文琦，王元全.基于梯度矢量卷積場的四階各向異性擴散及圖像去噪［J］.光學精密工程，2013，21（10）：2713－2719.Ren W Q，Wang Y Q.GVC－based fourth－order anisotropic diffusion for image denoising［J］.Optics and Precision Engineering，2013，21（10）：2713－2719.（in Chinese）

［7］ Aubert G，Kornprobst P.Mathematical Problems in Image Processing：Partial Differential Equations and the Calculus of Variations ［M］.New York：Springer，2006.

［8］ 陳仁喜，李鑫慧.基于各向異性插值模型的快速圖像修復方法［J］.計算機應用研究，2009，26（4）：1554－1556.Chen R X，Li X H.Fast image inpainting algorithm based on anisotropic interpolation model［J］.Application Research of Computers，2009，26（4）：1554－1556.（in Chinese）

［9］ 苗慧，宋光磊，張春紅，等.一種自適應各向異性的SAR圖像去噪算法［J］.遙測遙控，2011，32（1）：28－32.Miao H，Song G L，Zhang C H，et al.An adaptive anisotropic algorithm on SAR image denoising ［J］.Journal of Telemetry，Tracking and Command，2011，32（1）：28－32.（in Chinese）

［10］ 趙建.分數階微分在圖像紋理增強中的應用［J］.液晶與顯示，2012，27（1）：121－124.Zhao J.Fractional differential and its application in image texture enhancement［J］.Chinese Journal of Liquid Crystals and Displays，2012，27（1）：121－124.（in Chinese）

［11］ Groenewald A M，Arbard E，Otha E C.Related approaches to gradient－based thresholding［J］.Pattern Recognition Lett.，1993，14（7）：567－572.

［12］ Miller K S，Ross B.An Introduction to the Fractional Calculus and Fractional Differential Equations ［M］.USA：John Wiley ＆ Sons，1993.

［13］ 李艷，蘇萍，馬建設.立體投影質量的評價方法及系統［J］.液晶與顯示，2012，27（1）：31－37.Li Y，SU P，Ma J S.Evaluation method and system of stereoscopic projection quality ［J］.Chinese Journal of Liquid Crystals and Displays，2012，27（1）：31－37.（in Chinese）

［14］ 范媛媛，沈湘衡，桑英軍.基于對比度敏感度的無參考圖像清晰度評價［J］.光學精密工程，2011，19（10）：2485－2493.Fan Y Y，Shen X H，Sang Y J.No reference image sharpness assessment based on contrast sensitivity［J］.Optics and Precision Engineering，2011，19（10）：2485－2493.（in Chinese）

［15］ 劉希佳，陳宇，王文生，等.小目標識別的小波閾值去噪方法［J］.中國光學，2012，5（3）：248－256.Liu X J，Chen Y，Wang W S，et al.De－noising algorithm of wavelet threshold for small target detection［J］.Chinese Optics，2012，5（3）：248－256.（in Chinese）

［16］ 閻雪飛，許廷發，白廷柱.改進的固定點圖像復原算法［J］.中國光學，2013，6（3）：318－324.Yan X F，Xu T F，Bai T Z.Improved fixed point method for image restoration［J］.Chinese Optics，2013，6（3）：318－324.（in Chinese）