基于應變的X65懸空壓力管道失效長度分析
朱亞明,馬廷霞,張朋飛,陳紅霞
西南石油大學機電工程學院 (四川 成都 610500)
中石油西部管道公司所轄管線沿線地質地貌錯綜復雜,如蘭成渝管道,地形復雜,地震頻繁,河流多,且雨季長,經常出現埋地管道在洪水沖刷下形成局部懸空。地質災害頻繁發生,給管道的懸空長度、承載能力造成一定的影響,甚至發生斷裂,一旦發生危險,嚴重的可能造成油氣泄露污染環境,甚至可能燃燒爆炸,可見壓力管道的完整性直接關系到生產的安全[1-3]。X65管線鋼是油氣儲運中主要的集輸工具材料,具有良好的工藝和力學性能,管線鋼的應力-應變關系呈顯著非線性,因此精確描述管線鋼應力應變關系是管線鋼結構受力及穩定性分析等相關研究工作的基礎。本文對X65管線鋼的本構關系進行了研究并對其進行了修正。失效研究大多是基于應力的失效分析,研究表明在地震、滑坡、凍土等特殊工況環境下,懸空管道承受的應變和位移很大,雖已達到或超過應力判別的要求,但管道還能滿足輸送要求。用Abaqus軟件對X65懸空壓力管道進行有限元建模,對其進行基于應變的失效分析。
1 對X65管材的本構關系的研究
1.1 X65管材的本構關系
在萬能材料試驗機上,對X65(L450)鋼材試樣(10件)進行拉伸試驗,得到曲線(圖 1(a)),選取其中的一條典型的曲線(圖1(b))。
1.2 對X65管材理論本構關系研究及其修正
采用彈塑性理論建立其本構關系。由圖1可看出管線鋼進入塑性后,其應力應變表現為典型的非線性。在比例變形條件下,通過對增量理論的應力和應變增量關系的積分可得到全量理論的應力—應變關系。在此以全局二段式應力—應變模型為例分析。
第一階段為應力在條件屈服極限范圍內,即ε≤εp0.2(卸載后剩余0.2%的塑性變形所對應的應變,無量綱)時,采用傳統的Ramberg-Osgood本構模型來表示單軸非線性應力-應變關系;此模型視總應變ε總為彈性應變εe和塑性應變εp之和,其具體形式為:

圖1 X65(L450)管材的應力-應變關系曲線
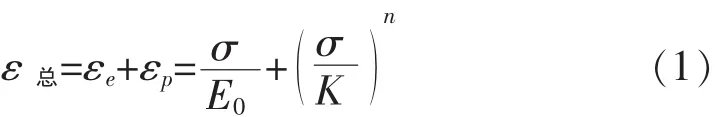
式中:σ為應力,MPa;K為應變硬化相關系數;E0為初始彈性模量,MPa;n為應變硬化指數。

式中:σs為屈服強度,MPa;ε0為初始應變 (ε0=σs/E0);n、r為 Ramberg-Osgood 參數。
X65管材中n=8,r=14,代入(2)得到X65管材的本構關系方程:

按照Ramberg-Osgood關系建立的曲線與X65管線鋼實驗本構關系曲線進行對比,如圖2所示。
由圖2知X65管材的應力—應變曲線在應變值比較低的情況下,方程(3)能夠準確地反應。但當應變高于條件屈服極限時的應變εp0.2以后,上述模型所求得的數值誤差較大,因此有必要對R-O模型做出修正。

圖2 X65管線鋼R-O模型與實驗實測值應力-應變曲線對比圖
第二階段為應變范圍在εp0.2<ε時,根據實驗數據,提出用條件屈服極限σp1.0來代替極限應力,在σp0.2和極限應力σp1.0間采用如下表達式[4],即:
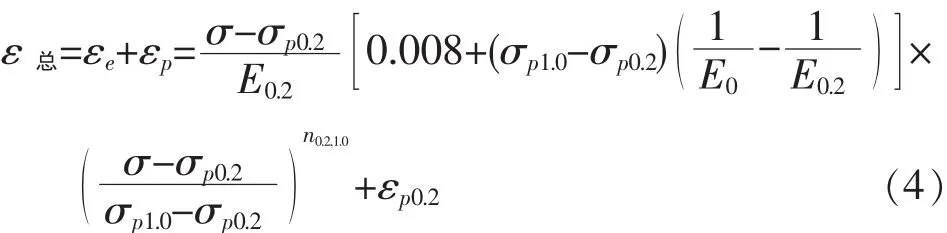
式(4)中,E0.2為應力等于σp0.2時的切線模量;εp0.2=0.2%,εp1.0=1%,與之對應的應力分別記為σp0.2和 σp1.0,n0.2,1.0為描述 σp0.2和 σp1.0間曲線段的應變硬化指數,其值可根據模型與實驗所得應力-應變曲線的符合程度求出。推導出此階段的應力應變關系式如下:

因此X65管材的本構關系具體表示為:

依據上述公式描述的應力-應變本構關系曲線如圖3所示。
由圖3,可以看到推導的公式與實驗曲線很好的擬合,即修正后的X65管材的Ramberg-Osgood關系式與實驗數據擬合得很好,此公式可以精確地反應X65管線鋼的應力應變關系。
2 懸空管道的應變極限
我國對于建立力學模型及懸空狀態下管道的基于應變失效的分析不多,但當管道遇到自然災害時,管道應力超過比例極限后的繼續變形,基于應力的設計已不再適用,此時基于應變的管道安全準則更為合理。挪威、加拿大等一些國家已經開始采用基于應變的設計準則[5]。基于應變的安全評估方法的關鍵,是確定管道在將要承受的應變及管道本身所能夠承受的應變極限,而這個應變極限可以通過有限元分析確定。
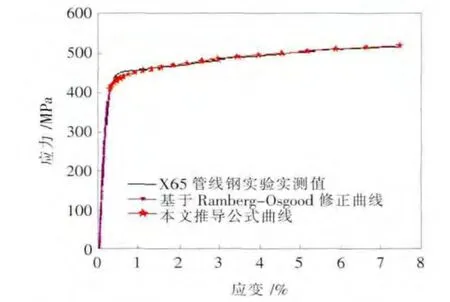
圖3 X65管線鋼實驗實測結果與各模型的應力-應變關系
2.1 拉應變極限
當管道存在缺陷時,拉伸應變達到或超過極限值,可能導致管道斷裂。為了防止薄膜斷裂,一次載荷、二次載荷或二者組合引起的拉伸應變應滿足以下因子化的載荷-阻力設計公式[6]:

式(8)中:εtf為縱向或環向的因子化拉伸應變;φεt為拉伸應變的阻力因子,可取0.7;εtcrit為管道的拉伸極限應變,由實驗確定,且應考慮缺陷、焊縫及熱影響區等,當缺乏具體信息時拉伸極限應變取0.75%,這是保守的取值,海底管線的取值為2%[7]。
2.2 壓應變極限
管線局部屈曲表現在管壁出現皺褶起紋,最終產生環管壁的裂縫。通過試驗研究 ,Hall和Newmark認為管線屈曲失效時的應變值為0.15t/R~0.20t/R。R為半徑 ,t為壁厚[8]。
應用基于應變的懸空管道失效判據,按拉應變極限,將 φεt=0.7,εtcrit=0.75%代入公式(8)得到 εtf≤0.525%;按壓應變極限,管線屈曲失效時的應變值為0.196 7%~0.26%。而在實際操作下,只要懸空管道進入塑性變形,就會對管道進行維護和搶修。因此本文采用極限懸空長度對應的最大應變值為0.525%,安全懸空長度對應的應變值為0.2%。
3 失效分析
3.1 工況概述
采用目前國際上先進的有限元分析程序Abaqus進行計算,懸空管道的力學建模借助大撓度梁理論、彈性地基理論、管-土互作用雙線性模型、Winkler彈性地基梁模型,考慮管道的幾何非線性和土壤的物理非線性[9-11]。由于結構與載荷在軸向與豎直方向具有對稱性,因此采用四分之一結構。對管道進行網格劃分,管體采用三維4節點減縮殼單元(S4R),土體采用 8節點線性減縮積分單元(C3D8R)。管道及土體和管道接觸部分網格劃分比較密集,遠離管道處的土體單元相對稀疏。
以X65管材為例,建立完全懸空管道的有限元計算模型,計算參數采用新疆烏鄯原油支干線段設計參數。管材塑性階段的本構關系由修正后的X65管材的Ramberg-Osgood關系式與試驗數據擬合的公式(7),代入應力值求得應變,見表1。
3.2 基于應變失效的懸空管道長度分析
本次分析分2組進行對比,2組數據都為X65管材,直徑為610mm的管子,在其他工況條件都相同的狀況下,第1組以管道內壓為變量,管道壁厚均為8mm,分析內壓為8MPa和10MPa時,在懸空長度為 50、100、150、200、300、400、520(560)、700m,時,得到應力應變關系,如圖4所示。第2組以壁厚為變量,管道內壓均為10MPa,分析在壁厚分別取8mm和10mm時的懸空長度與應變的關系,如圖5所示。
由圖4可以看到在懸空長度超過200m時,應變隨著懸空長度的增加呈線性增長,應力曲線斜率逐漸趨于零,這也驗證了基于應變的實效判別標準較為合理。在內壓為8MPa時,懸空長度為700m時,達到管道的屈服強度520MPa;以應變失效判別時,最大安全懸空長度為250m,極限懸空長度為430m。內壓為10MPa時,懸空長度為660m時,達到管道的屈服強度520MPa,以應變失效判別時,最大安全懸空長度為202m,極限懸空長度為350m。同時,由圖4知,在其他條件相同的工況下,內壓增大,管道應力應變值增加較快,管道的安全懸空長度和極限懸空長度將會減小。

圖4 內壓不同時懸空長度與應力應變關系圖

圖5 壁厚不同內壓相同的懸空長度與應變關系圖
由圖5同樣可以看到應變的增長隨著懸空長度的增大呈線性增長,在應變值為2.756‰~14‰間斜率增大使得應變增大更快。且在內壓相同的情況下壁厚越薄,應變越大。以應變失效判別,壁厚為8mm時,最大安全懸空長度為202m,極限懸空長度為350m。壁厚為10mm時,最大安全懸空長度為270m,極限懸空長度為431m。同時,由圖5在其他條件相同的工況下,壁厚減小,管道應變值增加較快,管道的安全懸空長度和極限懸空長度將會減小。
4 結論和建議
修正后的X65管材的Ramberg-Osgood關系式與實驗曲線擬合的很好,通過修正后的關系式可以更準確地得到X65管材的應力應變數據。
通過懸空長度與應力應變的關系曲線,驗證了基于應變失效的判別標準的合理性。
通過有限元分析,得到只有壁厚為變量時,最大安全懸空長度和極限懸空長度隨著壁厚的增大而增大;只有壓強為變量時,最大安全懸空長度和極限懸空長度隨著壓強的增大而減小。
當管道發生懸空,在安全懸空長度以內的管道可以等自然災害過后,再進行搶修;如果超出安全懸空長度時,建議立即對管道進行搶修。
[1]王為民,張文偉.黃土地區長輸管道地質災害分析及治理[J].油氣儲運,2001,20(4):28-31.
[2]馮慶善,陳健峰,艾慕陽,等.管道完整性管理在應對地震災害中的應用[J].石油學報,2010,31(1):139-143.
[3]O’Donnell H W.Investigation of flood induced pipeline failures on lower San Jacinto River[C].Proceedings of the Pipeline Division SpecialtyConference.New York,United States,ASME,2005.
[4]王孟鴻.鋼結構非線性分析與動力穩定性研究[M].北京:中國建筑工業出版社,2005.
[5]劉冰,劉學杰,張宏.基于應變的管道設計準則[J].天然氣工業,2008,28(2):129-131.
[6]Canadian Standards Association.CSA Z662-07,Oil and Gas Pipeline Systems[S].
[7]Det Norske Veritas(DNV).DNV-OS-F101,Submarine Pipeline Systems[S].
[8]高建,王德國,何仁洋,等.基于應變的懸空管道性能分析[J].管道技術與設備,2011(6):13-15.
[9]馬廷霞,吳錦強,唐愚,等.成品油管道的極限懸空長度研究[J].西南石油大學學報:自然科學版,2012,34(4):165-173.
[10]羅金恒,趙新偉,王峰會,等.地質災害下懸空管道的應力分析及計算[J].壓力容器,2006,23(6):23-26.
[11]楊毅,閆寶東,廖柯熹.輸油管道懸空管段應力計算[J].石油學報,2011,32(5):911-914.

