基于門限極值理論的湖泊水質參照狀態的確定
華祖林,汪 靚,顧 莉,褚克堅(1.河海大學淺水湖泊綜合治理與資源開發教育部重點實驗室,江蘇 南京 210098;2.河海大學水資源高效利用與工程安全國家工程研究中心,江蘇 南京 210098;3.河海大學環境學院,江蘇 南京 210098)
基于門限極值理論的湖泊水質參照狀態的確定
華祖林1,2,3*,汪 靚1,2,3,顧 莉1,2,3,褚克堅1,2,3(1.河海大學淺水湖泊綜合治理與資源開發教育部重點實驗室,江蘇 南京 210098;2.河海大學水資源高效利用與工程安全國家工程研究中心,江蘇 南京 210098;3.河海大學環境學院,江蘇 南京 210098)
在前人工作的基礎上,利用門限極值的廣義Pareto分布理論和超出閾值峰(Peak Over Threshold,POT)方法,提出了一種確定湖泊參照狀態濃度的新方法.該方法不僅能夠給出更為精確的置信區間,而且克服了廣義極值分布理論取用數據浪費等缺陷.將該方法應用到太湖的水質基準參照狀態中,通過POT方法對太湖8個站點1995~2006年總氮(TN),總磷(TP)和葉綠素a(Chl-a)的數據進行預處理,分別以-1.0mg/L, -0.05mg/L與-4μg/L作為它們觀測值相反數的門限值,結果表明觀測值的相反數符合廣義Pareto分布,驗證了方法的可行性.推薦采用25%分位點的值作為太湖總氮,總磷和葉綠素a的參照狀態,即太湖的參照狀態是:總氮0.66mg/L;總磷0.023mg/L;葉綠素a為1.27μg/L.最后分別得出了它們各自的95%置信區間,而且其精度明顯高于廣義極值分布理論結果.
湖泊水質基準;參照狀態;門限極值理論;置信區間
為了準確衡量人類活動對生態系統的影響,必須確定生態系統的營養物基準,而參照狀態濃度的確定是生態系統營養物基準制定過程中的核心環節之一.確定合理的參照狀態對制定營養物基準乃至整個生態系統的保護都有重要的意義.目前,人們公認的參照狀態濃度定義是由美國環境保護署[1]給出的,即“參照狀態是環境自然的,受到人類活動影響最小或環境系統可達到的最佳狀態”.
在當前情況中,特別是在經濟發達,人口稠密的區域往往很難找到符合參照狀態要求的湖泊,因此,國外研究者提出了參照湖泊法[2]、湖泊群體分布法[2]、古湖沼學反演法[2-3]、回歸分析法[2,4-5]、模型推斷法[2,6],三分法[7]等不同的建立參照狀態的方法:同時我國學者也在實踐中建立了國內不少湖泊的參照狀態濃度,并在理論上對方法提出了不少改進.如:鄭丙輝等[8]、陳奇等[9-10]根據太湖、巢湖和云貴高原湖泊的歷史數據采用頻率分析法建立了它們的參照狀態:李小平等[11]利用古湖沼學反演法建立了淀山湖的營養物基準:董旭輝等[12-14]利用類似的技術重建了太白湖等湖泊的營養物的歷史狀態;顧莉等[15]利用改進的形態土壤指數法推斷了太湖的總磷的參照狀態;張禮兵等[16]基于系統動力學推斷了巢湖的湖泊營養物參照狀態;華祖林等[17]提出的廣義極值法等.霍守亮等[18]總結了國內外學者在湖泊參照狀態上的工作;許秋瑾等[19]比較了東部湖泊和云貴湖區在營養物控制標準上的區別.表1歸納了常見的建立參照狀態方法及其優缺點比較.

表1 常見建立參照狀態方法Table 1 Popular methods for estimating the reference conditions of lakes
雖然確定湖泊參照狀態濃度的方法不少,但是,在實踐中,出于對成本和方法簡便易用性等問題的考慮,最常使用方法,如:參照湖泊法、湖泊群體分布法、三分法、頻率分析法等都是統計學方法.而從表 1可以看出這些統計學方法都有一些缺陷需要克服:湖泊群體分布法和參照湖泊法需要的數據量巨大且不太適用于污染比較嚴重的湖泊;三分法的分類標準較死板;頻率分析法雖然簡單,但是對受人類活動影響巨大的湖泊是可能高估湖泊參照狀態濃度的.更重要的是,以上這些統計學方法都未給出置信區間,因此難以評估其結果精度.
華祖林等[17]根據最小化人類對湖泊的影響以推斷湖泊參照狀態濃度的思想,利用廣義極值分布理論推斷了太湖總氮、總磷以及葉綠素 a的參照狀態濃度,并有效地給出了它們的置信區間.雖然廣義極值分布理論能夠給出湖泊參照狀態濃度的置信區間,但是由于這一方法在每年的觀測值中只取最小的一個觀測值,其余觀測數據均被舍棄,肯定造成觀測數據和信息的極大浪費.
針對多數統計學方法及廣義極值分布理論不同的缺陷,本文基于門限極值的廣義Pareto分布,采用超出閾值峰(POT)模型提出一種新的確定湖泊基準參照狀態的方法.該方法能很好的克服廣義極值分布理論的數據浪費和其他統計方法沒有給出置信區間的缺點,并運用該方法確定了太湖總氮、總磷和葉綠素a的參照狀態及其置信區間.
1 理論模型
從湖泊水質參照狀態的定義可以知道,對于太湖這樣受人類活動影響巨大的湖泊,其代表參照狀態的良好水質狀態是不太可能經常性的出現的.因此,為了最小化人類活動對湖泊水質的影響可以集中分析觀測值中優于一定水平的水質狀態以確定湖泊水質參照狀態.但是,需要注意的是一般常用的統計學方法并不適用于這種觀測值,而應該使用極值模型進行分析[20],門限極值理論就是極值模型的一種,并已經在相關學科領域表現良好[20-21].門限極值理論適用于對數據中較大值進行分析,而總氮、總磷和葉綠素 a等物質的濃度都是越小代表湖泊的狀態越好,因此需要取總氮、總磷和葉綠素a原始觀測值的相反數,以符合門限極值理論的要求,然后再進行分析.因此,本研究中總氮、總磷和葉綠素 a的負數是它們觀測值的相反數,這一步驟只是為了計算的需要而做的數學上的處理,是計算過程的需要[19-20],而相反數的值本身無特殊的意義.
具體主要思想是:若湖泊中特定物質如總氮,總磷和葉綠素 a等物質的月觀測值的相反數是平穩,無長時間相關性的;且其最大值構成的序列滿足廣義極值分布模型,則當 u→uend時有廣義Pareto分布成立:
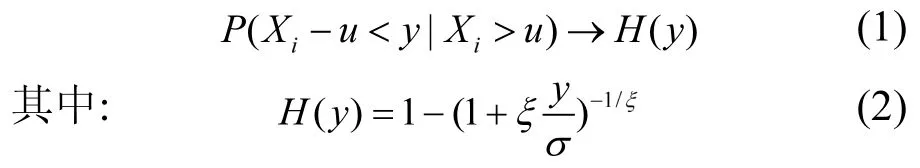
式中:Xi是觀測值相反數;uend是觀測值相反數Xi的右端點;y為一大于零的確定值;σ被稱為尺度參數;ξ被稱為形狀參數.u即是門限值,也就是說只有超過該值的觀測結果才參與模型的計算;特別值得指出的是門限值并不需要自己主觀指定,可以用很多方法確定,而在這里利用平均剩余壽命圖方法來確定.平均剩余壽命這個概念首先是來源于人壽保險和金融[20]等領域,即若定義 Xi的平均剩余壽命e(u)為:

式中:Nu是超出門限值u的觀測值相反數Xi的個數;u與 e(u)的關系圖就是平均剩余壽命圖.理論上可以證明若Xi滿足式(1)和式(2),則e(u)在其門限值附近是與u近似成線性[20-21];因此,可以用平均剩余壽命圖確定門限值u.
對于湖泊中的總氮、總磷等營養物的觀測值而言,該模型成立條件中的平穩性和無長時間相關性是比較容易滿足的,且可以用統計學方法檢驗其是否滿足;而其相反數的最大值滿足廣義極值分布理論這一點也已經在文獻[17]中得到論證.進一步,在實際應用中對于充分大的u0有:
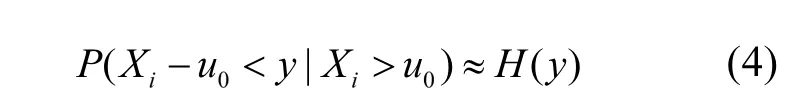
式(4)的2個參數有很多方法可以估計,最常用的就是極大似然法.主要思路是:假設 y1, y2,……,yk是k個超過閾值u0的觀測值,則H(y)的對數似然函數為:
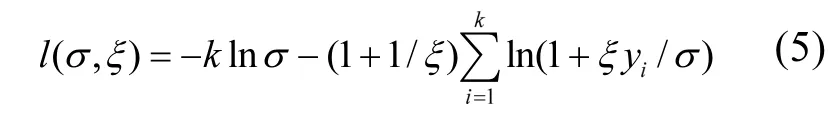
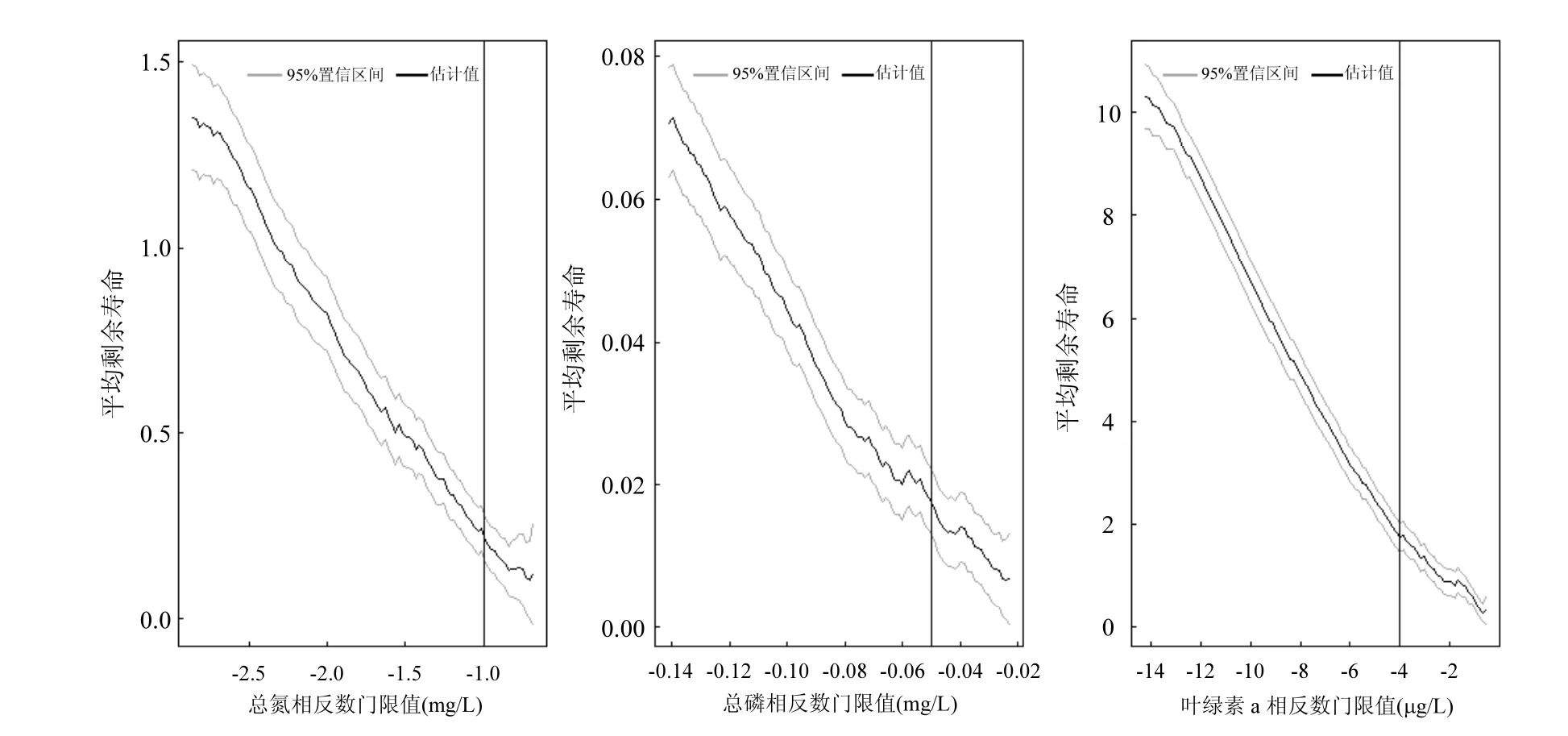
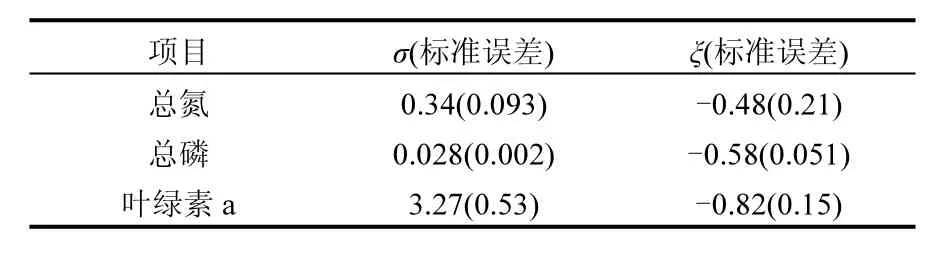
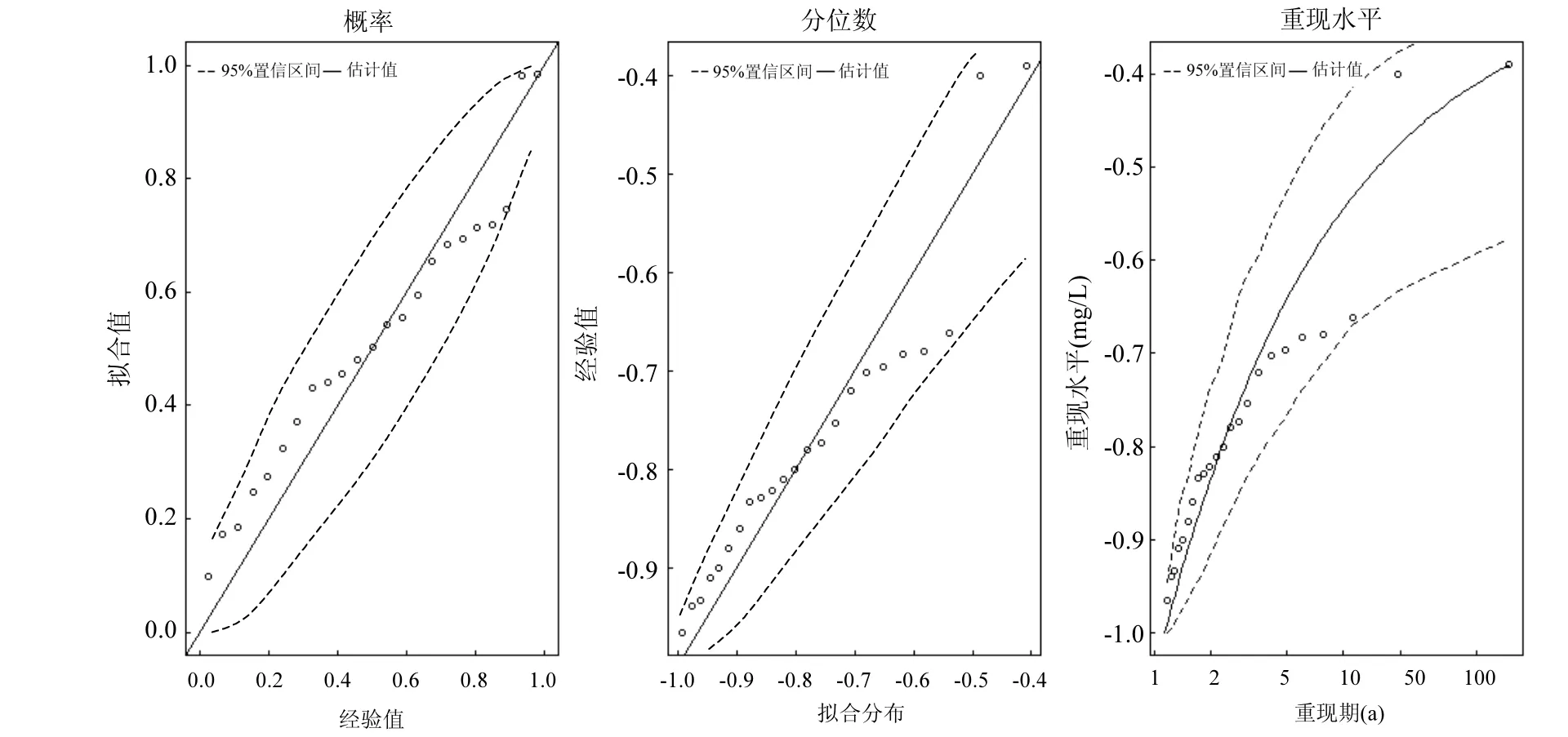
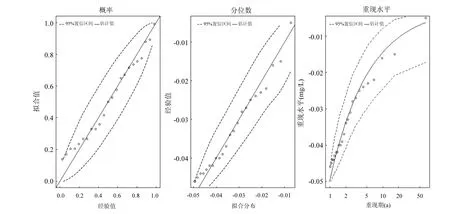
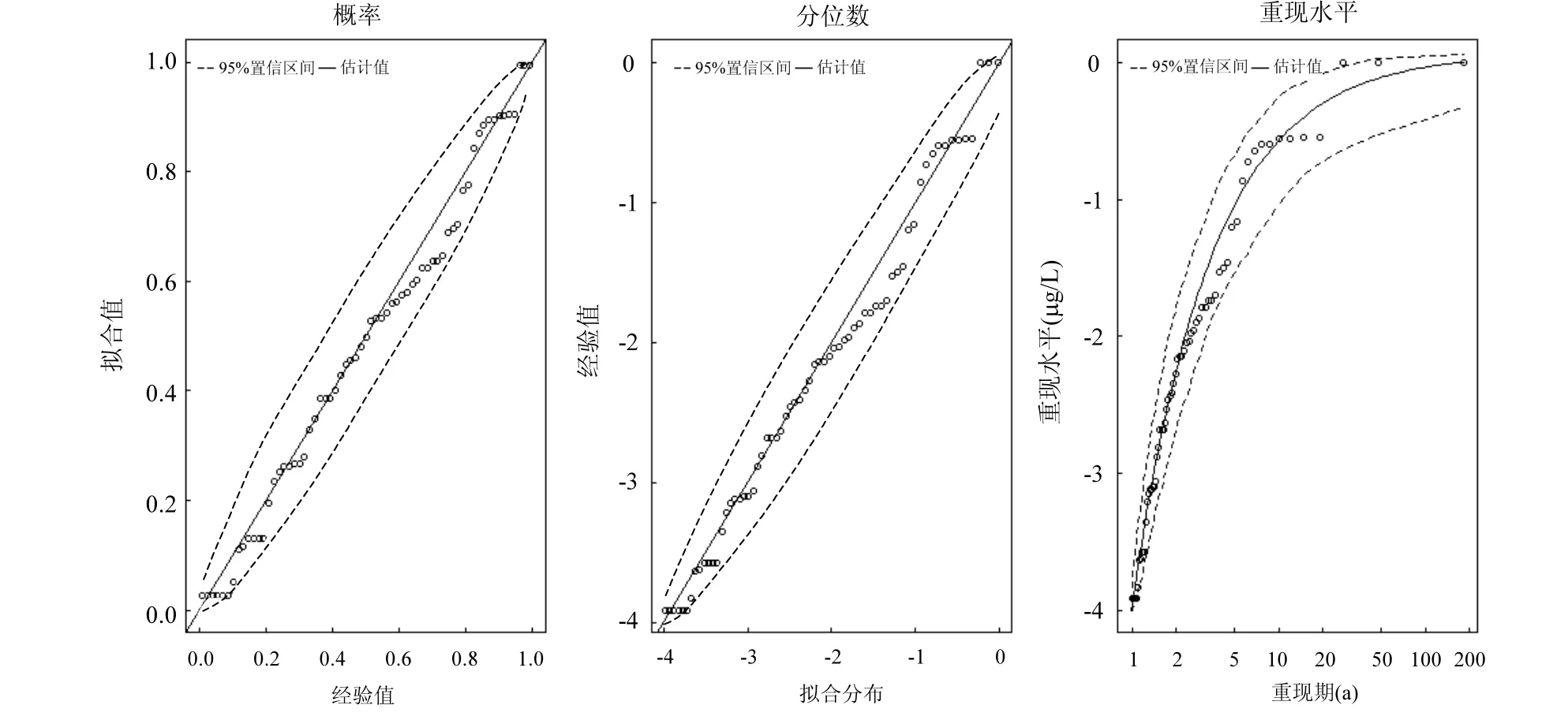
分別對σ,ξ求偏導,并令其等于零,則可以得到有關兩個參數的方程組進而求出 2個參數的值.在一般情況下這一方程組并無解析解,所以需要使用如 Guass迭代法等數值方法求解.得到出兩個參數值以后,對于0 式中:n為總觀測值的個數,Nu0為超過門限值 u0的觀測值相反數的個數.進而可以通過對數輪廓似然函數等方法估計置信區間,本文使用 Fisher方法估計置信區間. 2.1 數據來源 將門限極值模型應用于太湖參照狀態濃度的建立中,數據來源于“中國生態系統定位觀測與研究數據集—湖泊濕地海灣生態系統卷,江蘇太湖站(1991-2006)”[22].在本研究中將觀測的所有8個站點1995~2006年的數據都用于模型的建立,其中有極少數數據缺失,但是由于本模型并不基于時間序列的特性,因此少量數據的缺失并不影響模型的應用.根據前人研究結果,本文選用總氮,總磷,葉綠素a的觀測值進行分析,建立太湖的參照狀態濃度,每種物質有1145個數據. 2.2 數據預處理與POT方法 門限極值模型需要對每一個觀測數據取相反數,但是其廣義Pareto分布除了要求時間序列平穩且無長時相關性外,還要求超過門限值的觀測值不能連續出現,這一要求的本質是保證用于建立模型的觀測數據保持一定的獨立性.在現實中,超過給定門限值的觀測值往往會連續出現,如果時間序列中連續多個觀測值大于門限值,則這些觀測值就都會進入模型,從而使進入模型的觀測值之間具有較強的相關性,這樣就可能使該模型不再成立. 學者們提出很多不同的方法克服這一困難,比較常用的有馬爾科夫鏈方法,POT方法等[19].其中 POT方法思路清晰,計算結果優異[22],因此本文首先使用POT方法,根據一定的準則粗略的把連續觀測值分割成多個串,找出每個串的最大觀測值,然后再選擇適當的門限值,對這些最大值進行分析,構建門限模型,并進行統計檢驗. 目前為止,分割觀測值沒有規定的理論方法;本研究以保證分割后的序列能滿足統計理論要求和盡可能保留更多的觀測值為原則,經過反復試驗,確定以-2mg/L、-0.1mg/L和-15μg/L為標準分割太湖總氮、總磷和葉綠素a觀測值的相反數構成的序列依據:若連續4個月的觀測值低于這些給定的值,則這些連續的觀測值構成串,再將每一串觀測值中最大的數據取出參與極值門限模型的建立.值得指出的是,這里給定的這些分割標準遠遠的超出相關文獻中太湖參照狀態的范圍,因此這樣分割并不會影響最后的統計分析結果,又能保留更多的觀測值. 這樣處理以后得到太湖總氮、總磷和葉綠素a的觀測值中串的個數分別為77、97和127,顯然,這也是總氮、總磷和葉綠素 a的觀測值中真正參與建模的觀測值的個數. 3.1 門限值的選擇 對于門限模型來說,選擇一個恰當的門限值是非常重要的:若門限值太小,那么所選擇的數據可能嚴重偏離門限值模型:若門限值太大,那么超過門限值的觀測值數目就非常少,將影響所建立模型的可信度.學者們通過統計學上平均剩余壽命圖選取適當的門限值.當然,還需要參考所選取數值的環境學意義,綜合考慮才能得到好的門限值.圖1是總氮,總磷和葉綠素a的相反數通過預處理所形成序列的平均壽命.從圖1可見,在總氮和總磷的相反數的剩余壽命分別在-1.0mg/L與-0.05mg/L附近,是近似線性的,也就是說該門限值是滿足統計學要求的,且現行的湖泊總氮,總磷的三類地表水標準也是1.0mg/L與0.05mg/L,所以無論從統計學意義還是從環境學角度總氮和總磷相反數的門限值選為-1.0mg/L與-0.05mg/L是比較恰當的. 圖1 門限值選擇Fig.1 The Selection of a Threshold 對于葉綠素 a而言,根據太湖流域水資源保護局[24]推薦的湖泊富營養化評分與分類標準,結合圖1中葉綠素a的平均剩余壽命圖,確定選用-4μg/L作為葉綠素a相反數的門限值. 3.2 參照濃度的確定 表2 參數估計結果Table 2 The results of parameters estimation 表2是選擇門限值以后對總氮、總磷和葉綠素 a觀測值的相反數使用極大似然法估計參數的結果. 從表2可以發現,廣義Pareto分布的形狀參數及其 95%的置信區間都是負的,表明該模型有一個最大值,由于取了相反數,所以這意味著總氮,總磷和葉綠素 a的觀測值存在最小值.由于天然湖泊總氮、總磷與葉綠素a的濃度應該有最小值,所以這與實際情況是一致的.同時,這一結果也與廣義極值理論的結果一致[17].圖2~圖4分別顯示了總氮、總磷和葉綠素 a的模型參數檢驗及其95%置信區間的結果. 圖2 總氮相反數的模型檢驗Fig.2 Diagnostic plots of model fit to negative TN 從圖2~圖4可以看出,總氮,總磷的相反數都落在模型 95%置信區間以內,所以可以認為它們都符合門限極值模型;葉綠素 a雖然有一個值略微超出了重現期 95%的置信區間,但是超出的非常少,其它觀測值的概率圖、分位數圖以及重現水平圖都支持門限極值模型,再加上該觀測值出現在重現期很高的區域,不太可能使用該值附近的分位數作為參照狀態的依據,因此,可以認為葉綠素a也滿足門限極值模型是沒有問題的. 在選擇恰當的分位點作為湖泊參照狀態這個問題上,EPA[2]在參照湖泊法中推薦使用 25%的分位點的值作為湖泊的參照狀態;在國內,由于長江中下游的湖泊受到人類社會和經濟發展的影響較大,鄭丙輝等[8],陳奇等[9]學者在用頻率分析法,湖泊群體分布法等方法分析推斷太湖、巢湖的參照狀態時,采用所有觀測數據的 5%的分位點作為太湖和巢湖的參照狀態:華祖林等在用廣義極值理論推斷太湖參照狀態時,由于極小值已經代表現代太湖最好的狀態,他們也用 25%分位點的值作為參照狀態.在本研究中,考慮到門限模型理論選擇門限值過程已經去除了大部分水質不太好的情況,參與建立模型的觀測值本身就代表了水質良好的情況,使用 5%分位點的值作為參照狀態可能嚴重低估參照濃度,因此綜合考慮使用 25%分位點作為太湖參照狀態總氮、總磷和葉綠素a的濃度.表3是25%分位點的相關估計結果. 圖3 總磷相反數的模型檢驗Fig.3 Diagnostic plots of model fit to negative TP 圖4 葉綠素a相反數的模型檢驗Fig.4 Diagnostic plots of model fit to negative Chl-a 為了驗證結果的可靠性,將國內學者之前對太湖的參照狀態的研究與上述結果進行驗證與對比分析.同時,考慮太湖參照狀態研究結果不多,為了更好的驗證結果補充了與太湖情況相近的巢湖的相關研究結論,具體結果可見表4. 從表 4可以看到,鄭丙輝[8]等用頻率分析法給出了太湖總氮和總磷的參照狀態濃度分別為0.60mg/L及0.03mg/L,這一結果的總氮、總磷結果與本次研究得到的 25%分位點的值很接近.華祖林等[17]用廣義極值理論給出的太湖總氮與總磷的參照狀態濃度和 95%置信區間分別為0.71mg/L(置 信 區 間 為 :0.58~0.84mg/L)和0.025mg/L(置信區間為:0.018~0.033mg/L),顯然其結果是非常支持 25%分位點作為太湖參照狀態濃度的.顧莉等[15]用改進的MEI法給出太湖總磷的參照狀態濃度為 0.025mg/L,這一結果也本研究的結果非常接近.此外,20世紀60年代地理湖泊所對太湖調查[25]的研究表明,當時太湖總磷濃度在 0.01~0.05mg/L,其中位數為 0.03mg/L,考慮到20世紀60年代太湖的狀態良好,受人類活動影響較小,這一調查也支持將 25% 分位點結果作為太湖參照狀態濃度.陳奇等[9],張禮兵等[16]關于巢湖參照狀態的研究也給出了相近的結果. 表3 25%分位點的值及其95%置信區間估計Table 3 25thpercentile and 95% confidence intervals 表4 參照狀態結果Table 4 Reference conditions 先前的研究中關于葉綠素 a參照狀態的結果差異較大,鄭丙輝等[8]用頻率分析法給出太湖葉綠素a的參照狀態為4μg/L,高于本研究的結果,這可能是由于太湖在上世紀90年代以來藍藻的多次爆發,直接導致太湖葉綠素a濃度異常升高,從而引起頻率分析法對太湖葉綠素 a參照狀態的高估.華祖林等[17]給出的太湖葉綠素 a參照狀態濃度為1.81μg/L,置信區間為1.32~2.33μg/L,可以看作是對本次研究結果的支持.另一方面,不同方法建立的巢湖葉綠素 a參照狀態結果相差近10倍[9,16],這也表明在這一問題上爭議較大,但本研究給出的太湖葉綠素 a參照狀態結果在上述研究結果范圍內,表明本文給出的結論是可接受的.總之,用25%分位點作為太湖葉綠素a的參照狀態濃度是可以接受的.最后,需要注意的是,雖然廣義極值分布理論與本文的門限極值理論模型都能夠給出太湖總氮、總磷與葉綠素a參照濃度的置信區間.但是,門限極值理論由于能夠使用更多的觀測值參與建立模型,給出的置信區間精度明顯高于廣義極值分布理論的結果,這也是門限極值理論的優點之一. 門限極值理論在數學理論與方法更為復雜些,計算的工作量相對也大些,但對于計算機已經十分發達的今天,完全可編制計算程序,快速實現. 4.1 本文基于門限極值模型,提出了一種確定湖泊參照狀態濃度的新方法,該方法有效地克服了大部分已有的統計方法無法給出置信區間以及廣義極值分布理論對觀測數據造成很大浪費的缺點,推斷給出模型參數、營養物的參照狀態濃度和更為精確的置信區間. 4.2 以太湖為例,建立太湖的總氮、總磷和葉綠素 a觀測值的相反數構成的序列,驗證了其符合門限極值分理論布:并且和前人結果相印證,說明該方法是可行的.推薦將極值分布統計結果的25%分位點作為太湖參照狀態,即太湖總氮的參照狀態為0.66mg/L、總磷是0.023mg/L、葉綠素a為 1.27μg/L:它們相應 95%置信區間分別是: 0.55~0.77mg/L、0.022~0.025mg/L、0.84~1.70μg/L,這些置信區間長度都小于廣義極值分布理論的結果,這表明門限極值理論在精度上明顯優于廣義極值分布理論. [1] US EPA. Ambient water quality criteria recommendations:Information supporting the development of state and Tribal nutrient criteria, lakes and reservoirs in nutrient ecoregion II (EPA-822-B -00-007) [R]. Washington, D.C: US EPA, 2000: 6-30. [2] Gibson G, Carlson R, Simpson J, et al. Nutrient criteria technical guidance manual: lakes and reservoirs (EPA-822-B00-001) [R]. Washington, D. C: United States. Environmental Protection Agency, 2000:1-232. [3] Stockner J G, Benson W W. The succession of diatom assemblages in the recent sediments of Lake Washington [J]. Limnology and Oceanography, 1967,12(3):513-522. [4] Walter K D, Robert M O. A technique for establishing reference nutrient concentrations across watersheds affected by humans [J]. Limnology and Oceanography: Methods, 2004,2:333-341. [5] Vighi M, Chiaudani G. A simple method to estimate lake phosphorus concentrations resulting from natural, background, loadings [J]. Water Research, 1985,19(8):987-991. [6] Thèbault J M. Simulation of a mesotrophic reservoir (Lake Pareloup) over a long period (1983 -1998) using ASTER2000biological model [J]. Water Research, 2004,38: 393-403. [7] Walter K D, Edward C, Robert T A. Determining ecoregional reference conditions for nutrients, Secchi depth and Chlorophyll a in Kansas lakes and reservoirs [J]. Lake and Reservoir Management, 2006,22(2):151-159. [8] 鄭丙輝,許秋瑾,周保華,等.水體營養物及其響應指標基準制定過程中建立參照狀態的方法—以典型淺水湖泊太湖為例 [J].湖泊科學, 2009,21(1):21-26. [9] 陳 奇,霍守亮,席北斗,等.湖泊營養物參照狀態建立方法研究[J]. 生態環境學報, 2010,19(3):544-549. [10] 陳 奇,霍守亮,席北斗等.云貴高原湖區湖庫總磷和葉綠素a濃度參照狀態研究 [J]. 環境工程技術學報, 2012,2(3):184-190. [11] 李小平,陳小華,董旭輝,等.淀山湖百年營養鹽化歷史及營養物基準的建立 [J]. 環境科學, 2012,33(10):3301-3307. [12] 董旭輝,羊向東,劉恩峰.湖北太白湖400多年來沉積硅藻記錄及湖水總磷的定量重建 [J]. 湖泊科學, 2006,18(6):597-640. [13] 董旭輝,羊向東,王 榮,等.長江中下游地區湖泊現代沉積硅藻-總磷轉換函數 [J]. 湖泊科學, 2006,18(1):1-12. [14] 董旭輝,羊向東,潘紅璽.長江中下游地區湖泊現代沉積硅藻分布基本特征 [J]. 湖泊科學, 2004,16(4):298-304. [15] 顧 莉,李秋蘭,華祖林,等.確定太湖流域湖庫總磷參照濃度的改進MEI模型 [J]. 湖泊科學, 2013,24(3):347-351. [16] 張禮兵,霍守亮,周玉良,等.基于系統動力學的湖泊營養物基準參照狀態研究 [J]. 環境科學學報, 2011,31(6):1254-1262. [17] 華祖林,汪 靚.一種確定湖泊水質基準狀態濃度的新方法 [J].環境科學, 2013,34(6):2134-2138. [18] 霍守亮,陳 奇,席北斗,等.湖泊營養物基準的制定方法研究進展 [J]. 生態環境學報, 2009,18(2):743-748. [19] 許秋瑾,朱延忠,鄭丙輝,等.我國東部與云貴湖區富營養化控制標準與對比研究 [J]. 中國環境科學, 2011,31(12):2046-2051. [20] Coles S. An introduction to statistical modeling of extreme values [M]. 北京:世界圖書出版公司, 2008,45-73. [21] 史道濟.實用極值統計方法 [M]. 天津:天津科學技術出版社, 2005:4-65. [22] 秦伯強,胡春華.中國生態系統定位觀測與研究數據集—湖泊濕地海灣生態系統卷,江蘇太湖站(1991-2006)[M].北京:中國農業出版社, 2010. [23] 蘇懷智,王 峰,劉紅萍.基于 POT模型建立大壩服役性態預警指標 [J]. 水利學報, 2012,43(8):974-986. [24] 太湖流域水資源保護局.太湖流域及東南諸河省界水體水資源質量狀況通報 [R]. 2011. [25] 中國科學院南京地理研究所.太湖綜合調查初步報告 [M]. 北京:科學出版社, 1965:37. Estimation of the lake quality reference condition based on the threshold extreme theory. Liang1,2,3, GU Li1,2,3, CHU Ke-jian1,2,3(1.Key Laboratory of Integrated Regulation and Resource Development on Shallow Lakes, Ministry of Education, Hohai University, Nanjing 210098, China;2.National Engineering Research Center of Water Resources Efficient Utilization and Engineering Safety, Hohai University, Nanjing 210098, China;3.College of Environment, Hohai University, Nanjing 210098, China). China Environmental Science, 2014,34(12):3215~3222 A new method was established to calculate the lake nutrient reference condition based on the extreme threshold theory combined with the Peak Over Threshold. The new method not only revealed statistical inferences, but also overcame the weakness such as wasted observational data in generalized extreme value (GEV) theory. More accurate confidence intervals for parameters and substance concentrations could be obtained using this new method. The method was used to estimate the reference conditions of Taihu Lake. The observed data for total nitrogen (TN), total phosphorus (TP) and chlorophylla (Chl-a) at eight sites located in Taihu Lake during 1995~2006 were pre-treated by the Peak Over Threshold. The results revealed that negative values of TN, TP, and Chl-a, which the threshold values are ?1.0mg/L,?0.05mg/L, and ?4μg/L, fitted the generally Pareto model well. It was recommended to use 25thpercentile as reference conditions. Thus, the values of the reference conditions for TN, TP and Chl-a were 0.66mg/L, 0.023mg/L and 1.27μg/L, respectively. The 95% confidence intervals were also obtained, more accurately than using generally extreme theory. lake water quality criteria;reference condition;threshold extreme theory;confidence intervals X524 A 1000-6923(2014)12-3215-08 華祖林(1965-),男,江蘇江陰人,教授,博士,主要從事水環境模擬與污染物質輸移機制.發表論文100余篇. 2014-03-08 水體污染控制與治理科技重大專項課題(2012ZX07103-005);國家自然科學基金項目(51379060);江蘇省普通高校研究生科研創新計劃(CXZZ13_0271) * 責任作者, 教授, zulinhua@hhu.edu.cn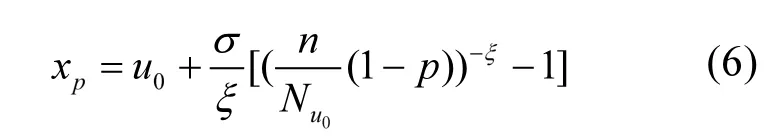
2 數據來源與處理
3 結果與分析
4 結論
HUA Zu-lin1,2,3*, WANG

