高壓渦輪全環非定常流動數值模擬

邵 飛 ，綦 蕾 ，羅建橋 ，劉東華

（1.北京航空航天大學能源與動力工程學院，北京 100191；2.中航工業動力機械研究所，湖南株洲 412002）

0 引言

渦輪內部流動受動靜干涉的影響，其流動本質上是周期性非定常的[1-3]，葉片排之間的相互作用對渦輪葉片通道內的流動產生不可忽視的影響，如尾跡、位勢作用、二次流和激波[4-8]等之間的相互作用，以及對流場的非定常擾動。尤其在高負荷跨聲渦輪中，在渦輪導葉出口存在很強的尾緣激波和反射波等各種波系，對流場中的非定常擾動更為明顯。從20世紀末開始，國內外學者已經開始密切關注高負荷跨聲渦輪中的非定常現象。Miller等[9]通過研究某跨聲高壓渦輪級下游的非定常流動，發現高壓渦輪級和下游靜葉之間具有復雜的3維相互作用；Davis等[10]對跨聲速高壓渦輪、過渡段和低壓渦輪進行數值模擬，詳細討論了高壓渦輪的動靜干涉、激波及其反射波對流場的非定常效應，以及對葉片表面壓力脈動的影響；鄒正平等[11]使用數值模擬方法研究了單級軸流渦輪內部上游葉片排尾跡和位勢作用對下游葉片表面負荷分布的影響，結果表明在渦輪級環境中，上游葉片排的尾跡對通道內部流動、邊界層流動損失的產生、發展和輸運以及下游葉片表面吸力面負荷分布均產生明顯的影響。

為了減小計算量以及獲得更加詳盡的細節流動，在非定常模擬計算中往往采用區域縮放法[12]對計算模型進行簡化，而模型中對各級葉片數的選取也僅從最大公約數的角度來考慮。Clack等[13]發現使用區域縮放法模擬出的2倍葉片通過頻率的擾動量級與未模化時的結果明顯不同，而后者與試驗結果更吻合。Yao[14]也通過對使用區域縮放法的算例進行數值計算并與試驗結果對比，證明了模化比例越接近于真實比例，計算結果越精確。因此，區域縮放法通過修改葉片幾何形狀導致非定常流動的預測精度受到污染，尤其是在各種擾動頻率的預測方面尤為突出。然而，對于全環渦輪內部非定常流動的數值計算研究相對較少[15]。

在具備大型并行機群硬件支持的條件下，本文嘗試利用CFD模擬真實情況下高負荷跨聲渦輪全環非定常內部流場，深入分析渦輪內部葉片排之間的非定常擾動，為高性能渦輪設計方法以及流場中的非定常擾動的預測提供參考。

1 研究方法

以某型高壓渦輪為研究對象，其幾何和氣動參數見表1。采用商用軟件CFX12.0求解3維非定常黏性雷諾平均N-S方程進行數值模擬，運用時間追趕的有限體積法進行數值計算。空間、時間離散分別采用2階迎風格式和2階后差歐拉格式，并運用多重網格技術加速收斂。湍流模型選用2方程k-ε模型。

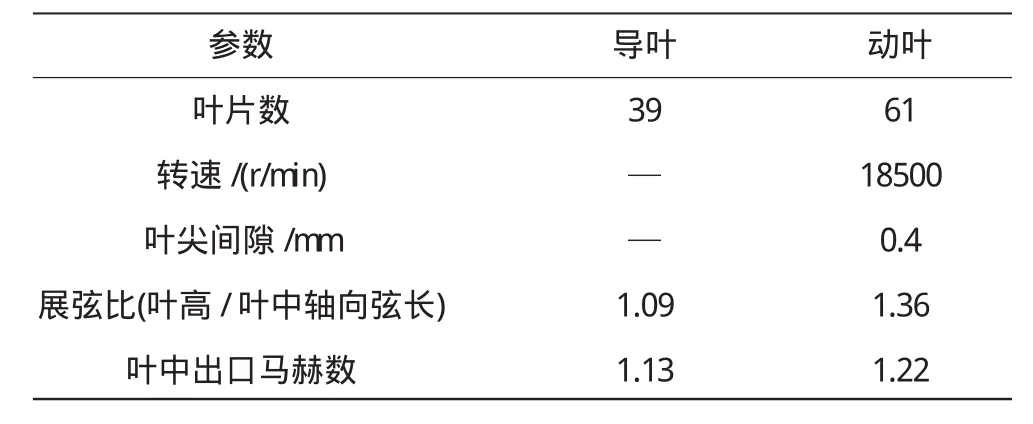
表1 高壓渦輪幾何和氣動參數

計算整體和布局網格如圖1所示。高壓渦輪定常計算網格總數為2092萬，包含高壓導葉網格數873萬（單通道網格數22.4萬）、高壓動葉1219萬（單通道網格數20萬）、導葉和動葉沿展向34個網格；高壓動葉葉尖間隙為0.4mm，展向給了7個網格節點。

采用1條槽縫來代替1排氣膜孔的方法來模擬冷氣流動，其中1條槽縫的面積近似等于1排氣膜孔面積的總和。冷氣邊界條件給定質量流量、冷氣流動方向角、冷氣總溫、冷氣湍流度和渦黏性比。在軸向間隙處，冷氣流動方向與旋轉軸正方向之間的夾角約為30°；進口湍流度為5%。

圖1 計算整體和局部網格

在計算中，進口邊界條件給定總溫、總壓和氣流角。其中總溫按照已知進口總溫沿展向的分布，總壓展向均勻分布，來流設為軸向,出口給定靜壓平均值。計算工質的設定根據油氣比計算變比熱模擬真實燃氣，壁面邊界條件設為固壁絕熱和無滑移條件。導葉與動葉的交界面以及單通道與其余通道之間的交界面均采用直接差值的方法。

在具體計算時，設定動葉旋轉1個非定常周期為800個物理時間步，動葉通過1個導葉通道約用20個時間步。每個虛擬時間步設為10。為方便判斷非定常計算是否穩定，在動葉前緣和尾緣附近分別設置監測點（如圖2所示），分別監測各點處流場的靜壓和軸向速度。在計算各狀態點時，首先計算2400個時間步長，得到穩定的計算結果，然后再讀取800個時間步長的瞬時結果并輸出其統計平均結果。定常與非定常數值模擬計算在大型并行機群上進行，使用8×10個核心（內存160G），計算耗時約1個月。

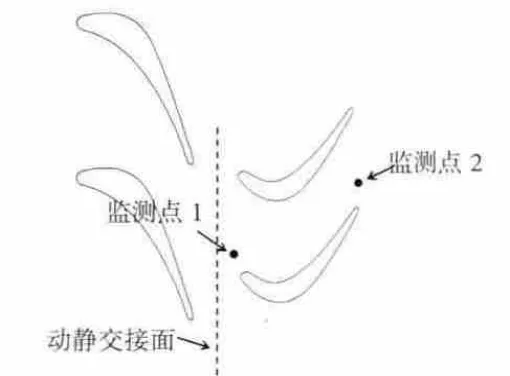
圖2 監測點位置（50%葉高）

2 結果分析

2.1 監測點變量隨時間的變化

非定常計算結果穩定后2個監測點處靜壓和軸向速度隨時間的變化如圖3所示。橫坐標表示時間，并以動葉旋轉1周的時間T做無量綱處理。從圖中可見，監測點的靜壓和軸向速度呈現出良好的周期性，說明非定常計算結果收斂較好。在動葉通過導葉通道時，監測點1處的靜壓和軸向速度基本呈現出周期性波動，在動葉旋轉1周后共歷時39個小周期性波動；監測點2處的靜壓和軸向速度同樣也存在周期性，與監測點1處不同的是，其在1個周期內存在4個較小的周期性波動。下文將對此作詳細分析。

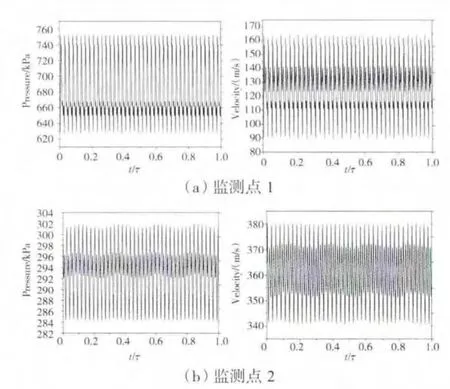
圖3 非定常計算監測點變量隨時間的變化

2.2 導葉非定常流動

高壓導葉葉根、葉中、葉尖表面等熵馬赫數分布如圖4所示。圖中藍線是時間平均值，黑、紅線分別是1個周期內當地等熵馬赫數的最大值和最小值。從圖中可見，葉片表面的非定常負荷脈動，吸力面靜壓最大脈動位置在0.8～1.0軸向弦長范圍內，而在其他位置葉片表面幾乎沒有壓力脈動。說明導葉通道內的流場受非定常效應的影響很小，范圍也僅限于導葉吸力面尾緣附近。從圖4（d）中的馬赫數云圖（時均結果）中可見，在導葉尾緣存在較強的燕尾波，其內尾波分支撞擊在相鄰導葉吸力面并發生反射。內尾波的存在導致下游動葉非定常效應對上游的影響受限于吸力面下游附近。

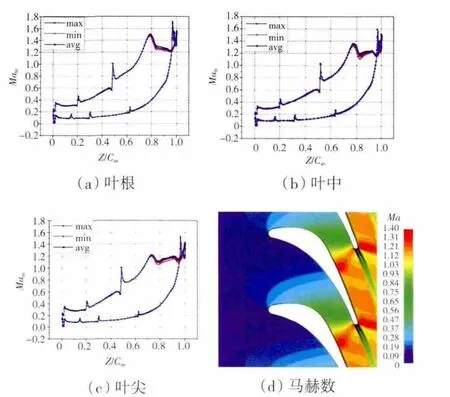
圖4 導葉表面等熵馬赫數分布及50%葉高馬赫數

導葉出口截面50%葉高處靜壓分布如圖5所示。橫、縱坐標分別表示導葉節距和時間，其中τ為動葉經過1個導葉通道的時間。

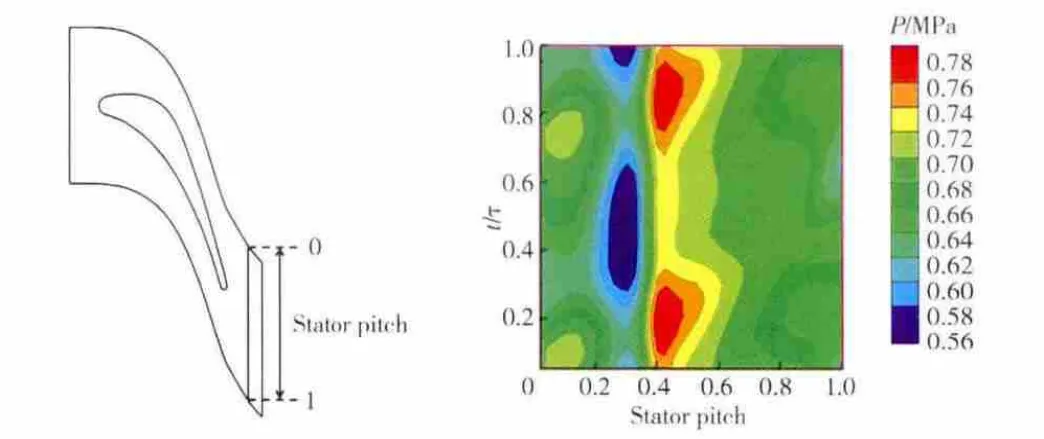
圖5 導葉出口截面50%葉高處靜壓分布

從圖中可見，在下游無動葉的情況下，靜壓分布不隨時間變化，圖中的等值線應該平行于豎直方向，而下游動葉排的周期性掃過導葉出口流場，使得在導葉出口激波位置發生周期性變化，同時也引起導葉吸力面尾緣附近的負荷脈動。在0.1節距位置處也出現靜壓周期性變化的現象，此處對應的位置為導葉尾緣激波的內尾波經相鄰導葉吸力面后產生的反射波，其位置也隨動葉的轉動而呈周期性變化。導葉尾緣激波的非定常變化將直接影響動葉表面的負荷分布。

2.3 動葉非定常流動

在動葉中采用靜壓系數來描述葉片表面的負荷分布

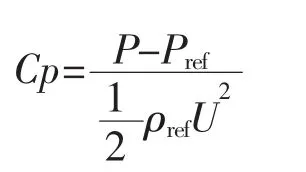
式中：Pref、ρref分別為時均結果動葉進口截面平均值；U為動葉各葉高處的牽連速度。

動葉的葉根、葉中、葉尖表面靜壓系數分布如圖6所示。從圖中可見，靜壓的脈動幅度相對較大，葉片表面負荷分布形式的變化也很大，意味著動葉表面受到很強的非定常氣動力作用。結合導葉出口處壓力場的時空圖可知，導致動葉表面很強的非定常效應主要有以下原因：（1）在上游導葉出口有很強的燕尾波，其外尾波分支周期性作用于動葉前緣，產生很強的非定常效應；（2）由于導葉負荷分布是后加載葉型，尾緣負荷很大，導致對下游的位勢作用很強；（3）導葉出口尾跡的作用。

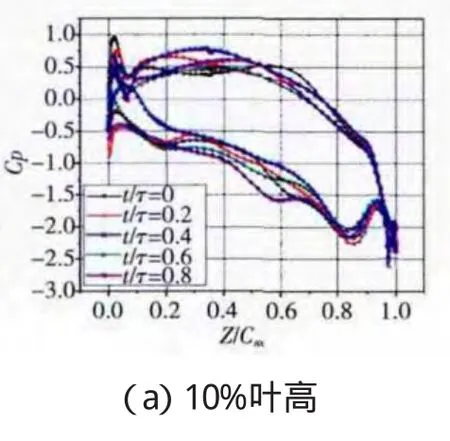
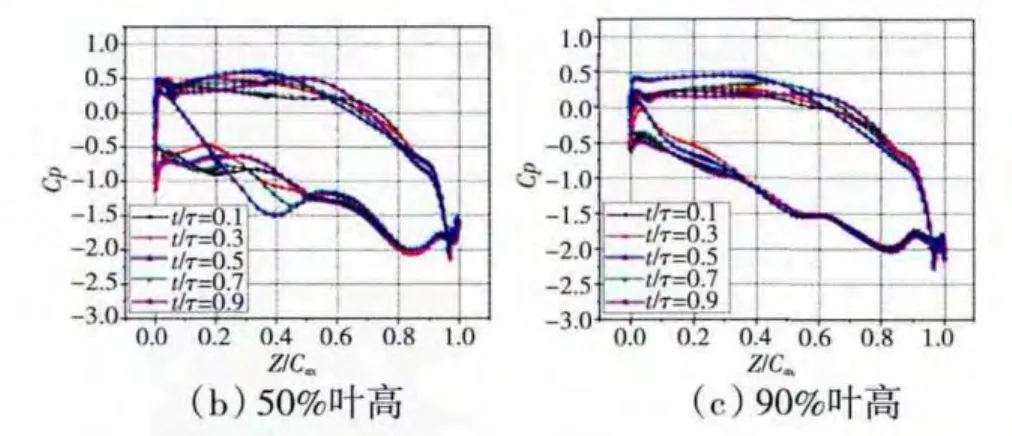
圖6 動葉表面靜壓系數分布

2.4 上游尾跡和激波對下游流場的擾動

不同瞬時時刻50%葉高位置擾動速度矢量在通道中的分布如圖7所示，其定義為瞬時與時均速度矢量之差。由尾跡形成的逆射流周期性地被下游葉片切斷之后繼續向下游傳播，并對氣流產生從壓力面到吸力面的相對輸運。在尾跡上、下游附近位置出現1對方向相反的渦，分別對尾跡下游和上游流場加、減速。對比t和t+0.25τ時刻，葉片最大厚度位置處在尾跡經過前后產生方向相反的擾動速度，會引起或者增加葉片表面壓力脈動，進而引起葉片負荷分布的變化。隨著尾跡的輸運，擾動渦對影響的范圍也逐漸擴大，但上、下游渦核心向下游輸運的速度明顯不同。在t+0.75τ時刻，尾跡下游的渦核心隨著尾跡輸運至動葉尾緣附近，而尾跡上游的渦核心則位于0.5倍的軸向位置處，意味著擾動渦對引起的葉片表面脈動與尾跡通過頻率一致，但葉片表面脈動滯后于尾跡的輸運。

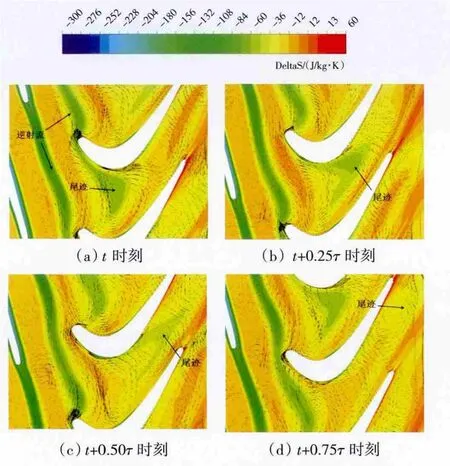
圖7 不同瞬時50%葉高位置擾動速度矢量及熵增分布

激波在葉片通道之間傳播的相對位置如圖8所示。激波A、C指在不同位置處的外尾波，B指內尾波及其反射波。

不同葉高動葉表面靜壓系數如圖9所示。橫、縱坐標分別為動葉經過1個導葉通道的周期數和動葉軸向弦長的無量綱數。從圖中可見，在動葉表面已知葉高任一位置的靜壓隨時間的變化過程。吸力面和壓力面的分隔點位于動葉軸向位置的最左端和最右端。導葉尾緣激波外尾波分支首先作用于葉片吸力面頂點附近，并隨時間變化逐漸向上游遷移直至動葉前緣，之后再作用于壓力面0.6軸向距離。內尾波分支則經相鄰導葉吸力面反射后也以類似方式作用于動葉吸力面。從激波相對動葉的運動軌跡可見，隨著動葉的旋轉，激波在吸力面是從下游向上游推進，反映在圖中為從左上到右下方向的壓力梯度對角線。吸力面在圖中顯示在0～0.4軸向位置由導葉尾緣激波引起較大的周期性變化的壓力波動，尤其是在0.1軸向位置附近，壓力隨時間的變化最為劇烈。

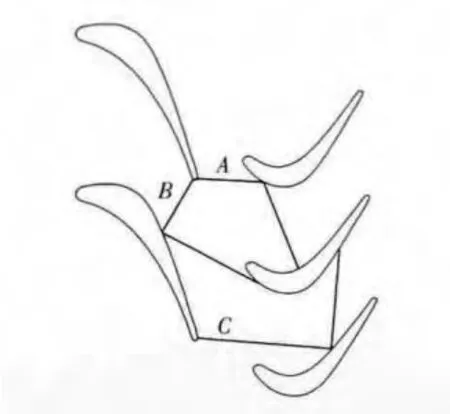
圖8 激波在葉片通道之間傳播的相對位置

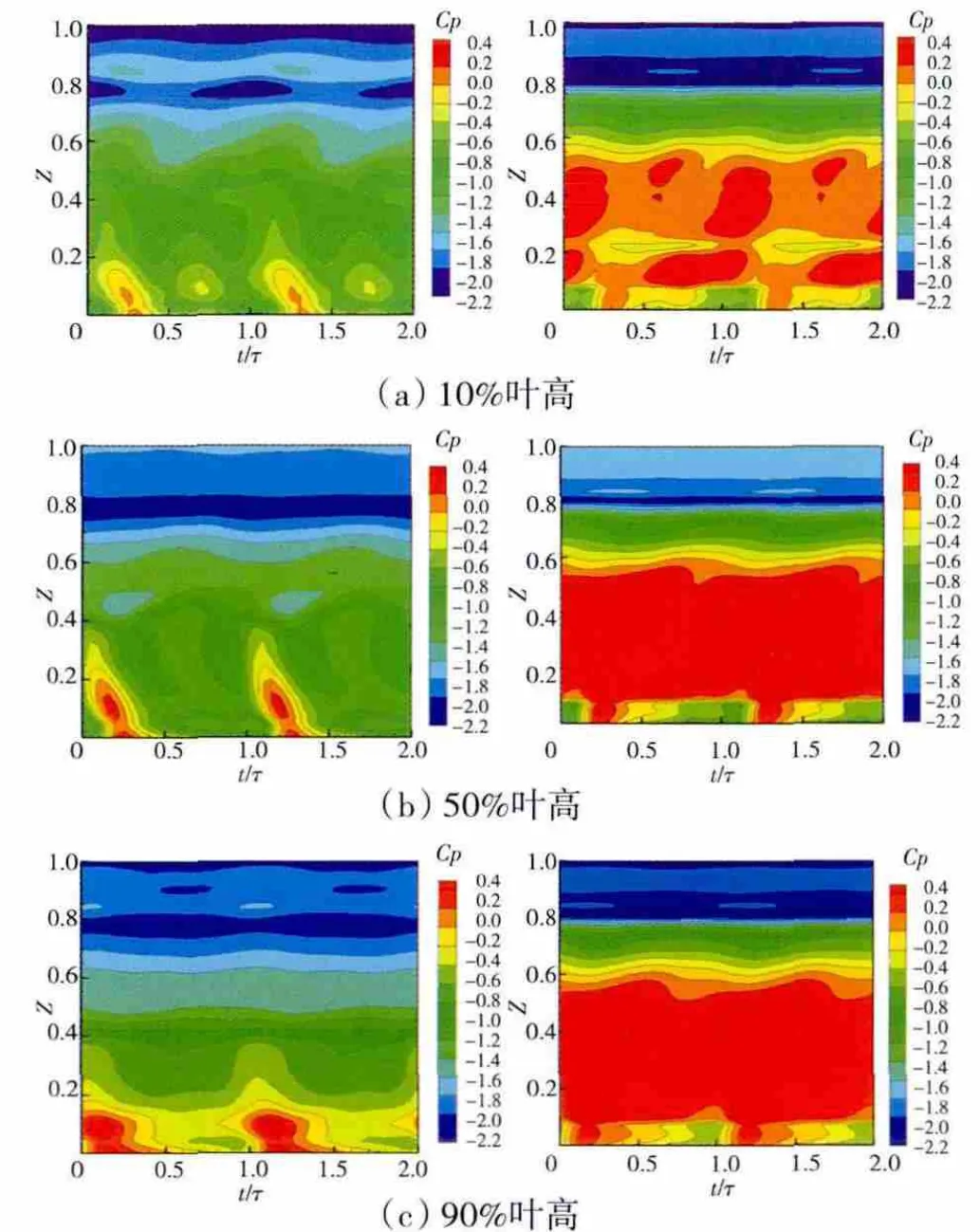
圖9 不同葉高動葉表面靜壓系數(左為吸力面，右為壓力面)

導葉尾跡通過動葉通道時，對其吸力面、壓力面的影響均為從上游向下游發展，在圖9中一致表現為從左下到右上方向的壓力梯度對角線。從圖9中可見，在壓力面0.1～0.6軸向位置處的壓力受尾跡作用影響，呈現周期性變化。在壓力面0.7軸向位置的下游的表面壓力受尾跡作用很小；在壓力面0.1軸向位置的上游仍會受到外尾波和內尾波的反射波的影響，此處激波在壓力面推進的方向與尾跡相同。

圖8中C處外尾波經過動葉壓力面后反射到相鄰動葉吸力面上，其運動方式在圖9中表現為從左上到右下方向的壓力梯度對角線，而圖9中顯示的方向是與壓力面相同方向的壓力梯度對角線。表明在吸力面0.5軸向位置下游受C處外尾波影響較小，受導葉尾跡的影響較大，在圖9中顯示的方向與導葉尾跡的傳播方向一致。

綜上所述，在動葉吸力面0～0.4倍軸向長度區域，激波引起明顯的高壓力梯度，而在0.5～1.0倍軸向長度區域，尾跡對吸力面的壓力影響較大，在10%葉高處可以較清晰地看到由內尾波的反射波引起的壓力梯度，而在其他葉高位置處，此反射波影響不大。在壓力面，除前緣附近受激波的影響外，葉片表面的壓力脈動主要受上游尾跡作用影響，在0.7～1.0倍軸向長度區域則受尾跡影響很小。圖中各葉高的時空圖均表面，導葉尾緣激波引起的動葉表面非定常壓力脈動幅度要大于導葉尾跡的，尾緣激波對下游動葉表面負荷分布的影響比導葉尾跡作用產生的影響更大。

從圖9中還可見由導葉、動葉幾何關系引起的不同葉高處激波相對于動葉的位置變化。對比10%、50%和90%葉高激波位置可見，在葉尖前緣位置最早受到導葉尾緣激波的影響，但激波強度相對不大，引起的壓力脈動幅度較小。經過約0.15個動葉通過周期后，導葉葉中位置的激波移動到動葉前緣位置，此時激波引起的壓力脈動幅度最大；最后受到激波影響的位置在動葉根部，激波強度與葉中相比有所減弱。

動葉進口距前緣約16%軸向長度位置沿各葉高處的靜壓分布如圖10所示。橫、縱坐標分別表示動葉節距的無量綱數和其經過上游1個導葉柵距的時間。在10%葉高位置，清楚可見在0.56軸向距離位置處，由激波和其反射波引起的壓力脈動。在50%葉高位置膨脹波對進口靜壓分布的影響較為明顯，膨脹波的位置是隨動葉與導葉的相對位置變化而變化的，故在圖中并沒有呈現與激波作用明顯相同（從左上到右下對角線）的趨勢。A-A和B-B位置處的靜壓系數隨時間的變化如圖11所示，分別反映了激波、反射波和膨脹波對壓力場分布的影響。

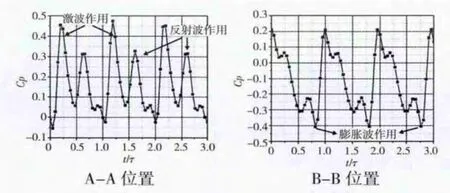
圖11 不同位置靜壓系數隨時間的變化

2.5 低頻擾動

從如圖3所示的監測點處各參數的時間變化可見，監測點1處的靜壓值和軸向速度由于動葉掃過導葉出口處的流場時，受到激波和尾跡的擾動而呈現出非常均勻地周期性變化。靜壓和軸向速度經過FFT變換后的頻譜如圖12所示。從監測點1的頻譜分析可以看出主頻（NPF）對應于轉子通過1個導葉通道的頻率，同時也是激波和尾跡作用于動葉通道內流場和葉片表面的頻率。另外，葉尾緣激波和尾跡的位置也存在由動葉周期性掃過導葉出口流場引起的周期性變化。

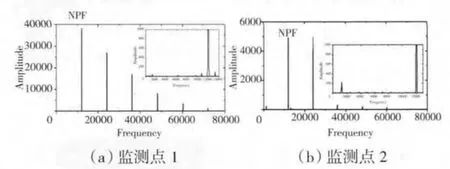
圖12 靜壓頻譜分析

受上述諸多因素的影響，動葉通道內的靜壓和軸向速度除了存在上述擾動外，還存在低頻擾動。從監測點2靜壓頻譜分析中清楚可見這種低頻信號，其頻率約為主頻的10%，即動葉完整旋轉1周出現4次周期性的波動。

動葉表面50%葉高位置選取8個關鍵點處的靜壓（無量綱）隨時間的變化如圖13所示。其中點1位于葉片前緣，點2、3分別位于激波最遠作用點的上、下游，點4、5分別位于動葉激波上、下游，點6～8分別位于壓力面前緣、葉中和尾緣附近。各點處的靜壓波動幅值均有所不同，幅值變化最大和最小的位置分別位于點1、8位置處。對比發現從點2到3位置，葉片表面靜壓波動程度明顯減小，而且在點3位置處清晰可見上述提到的低頻擾動。另外，在壓力面上點7位置處仍可以受到導葉尾緣激波的影響，其壓力波動的幅度與點6處的相比變化不大。激波向下游傳播時強度越來越弱，到點8位置處激波對葉片表面靜壓波動的影響消失，尾跡的影響也有所減弱，而低頻擾動仍然存在。從動葉出口的靜壓波動情況來看，低頻擾動對渦輪總體性能參數影響很小，而對局部細節的流場影響相對較大，如在點3位置處低頻靜壓脈動量占動靜干涉引起脈動量的8%。

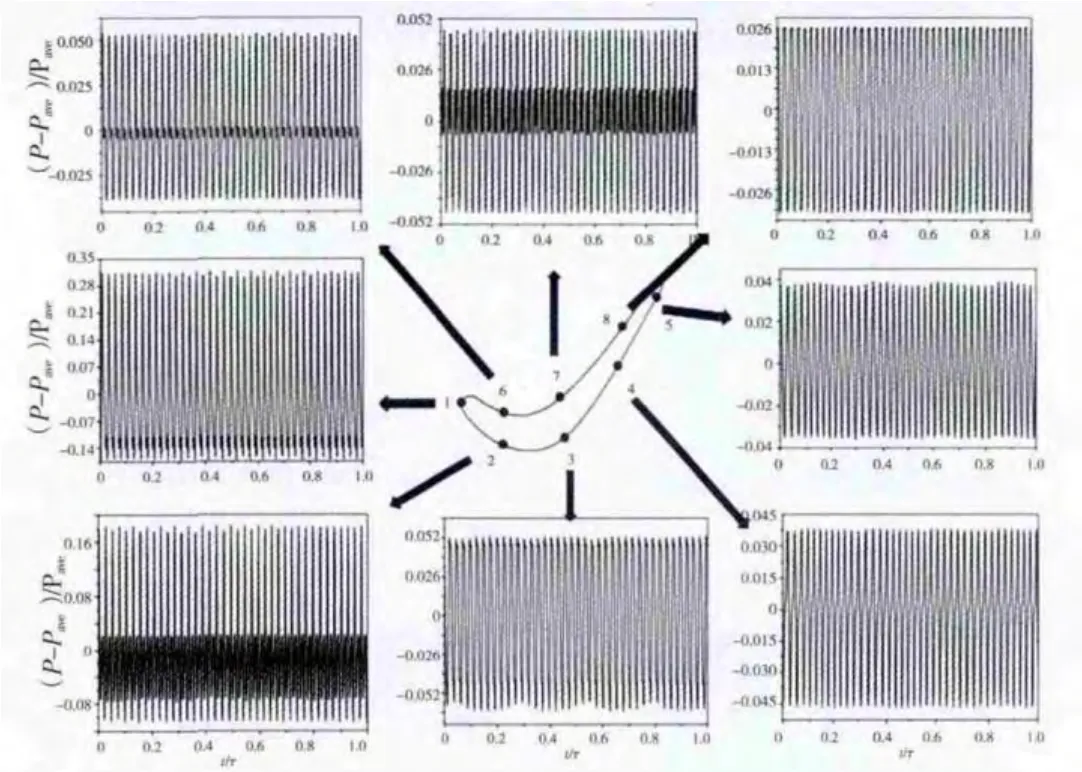
圖13 動葉表面各點的相對靜壓變化（50%葉高）

3 結論

（1）引起高壓渦輪內部非定常流動的因素主要有激波、位勢和尾跡作用等。計算結果顯示由導葉激波引起的非定常效應最為明顯，其作用在動葉葉片表面，引起強烈的壓力波動。尾跡對動葉內部流場的影響也是不可忽略的，動葉壓力面和吸力面0.5倍軸向弦長位置下游處的靜壓波動很大程度上是由于尾跡輸運導致的。

（2）從監測點處靜壓變化可見，在動葉通道內靜壓波動最大區域對應于導葉激波通過時刻，波動相對較小的區域對應于內尾波的反射波通過時刻，而尾跡的影響則很小。

（3）從監測點的變量及動葉葉片表面各關鍵點的靜壓變化數據可知，除了由導葉激波和尾跡引起的動葉通道及葉片表面靜壓周期性脈動外，還存在1種低頻擾動，其頻率遠小于動葉通過頻率。從動葉出口的靜壓波動情況來看，低頻信號對渦輪總體性能參數影響很小，而對局部流場影響相對較大。

（4）從全環非定常計算結果可知，采用區域縮放法按最大公約數簡化模型（如在本算例中模化為2∶3），在預測動葉通道內流場中的各種非定常擾動時必然產生較大誤差，模化后的流場抹消了流場中存在的低頻擾動。

致謝

感謝北京航空航天大學能源與動力工程學院鄒正平教授在本課題研究中給予指導和幫助！

[1] Sharma O P，Pickett G F，Ni R H. Assessment of unsteady flows in turbines [J]. Journal of Turbomachinery，1992，114（1）：79-90.

[2] Pollan G. Secondary flows and loss caused by blade row interaction in a turbine stage [J]. Journal of Turbomachinery,2006，128（3）：484-491.

[3]季路成，周盛.轉/靜干擾效應納入設計體系的途徑探索[J].工程熱物理學報，1999，20（5）：580-583.

JI Lucheng, ZHOU Sheng. Exploration of the rotor-stator interaction applying to design system[J]. Journal of Engineering Thermophysics，1999，20（5）：580-583.（in Chinese）

[4] Casciaro C，Treiber M，Sell M. Unsteady transport mechanisms in an axial turbine [J]. Journal of Turbomachinery，2000，122（4）：604-612.

[5] LaGraff J E，Ashpis D E，Oldfield，et al. Unsteady flows in turbomachinery[R]. NASA-CP-2006-214484.

[6]綦蕾.渦輪端區非定常相互作用機理及流動控制技術探討[D].北京：北京航空航天大學，2010.

QI Lei. Investigation of unsteady interaction mechanism and flow control in the turbine endwall regions[D]. Beijing: Beihang University，2010.（in Chinese）

[7] Kachel C E, Denton J D. Experimental and numerical investigation of the unsteady surface pressure in a three stage model of an axial high pressure turbine[J]. Journal of Turbo ma chinery，2004，128（2）：261-272.

[8] Giles M B. Stator rotor interaction in a transonic turbine [J].Journal of Propulsion and Power，1990，6（5）：621-627.

[9] Miller R J，Moss R W，Ainsworth R W，et al. The development of turbine exit flow in a swan-necked inter stage diffuser [R].ASME 2003-GT-38174.

[10] Davis R L，Yao J X，Clack J P，et al. Unsteady interaction between a transonic turbine stage and downstream components [J]. International Journal of Rotating Machinery，2004，10（6）：495-506.

[11]鄒正平,葉建,張永新，等.非定常流動對葉片表面負荷分布影響的數值模擬研究[J].燃氣渦輪試驗與研究，2006，19（1）：21-26.

ZOU Zhengping, YE Jian, ZHANG Yongxin, et al. Numerical simulation of unsteady flow effects on turbine blade loading distributions [J]. Gas Turbine Experiment and Research，2006，19（1）：21-26 .（in Chinese）

[12] Rai M M. Multi airfoil Navier-Stokes simulations of turbine rotor stator interaction [J]. Journal of Turbomachinery，1990，112：377-384.

[13] Clack J P，Stetson G M. The effect of airfoil scaling on the predicted unsteady loading on the blade of a 1 and 1/2 stage transonic turbine and a comparison with experimental results [R]. ASME 2000-GT-0446.

[14] Yao J X, Davis R L. Massively parallel simulation of the unsteady flow in an axial turbine stage [J]. Journal of Propulsion and Power，2002，18（2）：465-471.

[15] Vahdati M，Sayma A，Imregun M. Prediction of high and low engine order forced responses for an LP turbine blade [R].AIAA-98-3719.