Adaptive Angular Velocity Tracking Control of Spacecraft with Dynamic Uncertainties＊

Qiao Bing（喬兵），Liu Zhenya（劉振亞），Hu Bingshan（胡冰山），Chen Meng（陳萌）

1.College of Astronautic，Nanjing University of Aeronautics and Astronautics，Nanjing，210016，P.R.China；2.Institute of Aerospace System Engineering Shanghai，Shanghai，201109，P.R.China

1 Introduction

Angular velocity tracking of spacecraft has important applications in the area of space exploration.For example，rigid spacecrafts，such as satellites for surveillance or communication，often have to conduct large and rapid maneuvers for accurate slewing and／or pointing，which require the spacecraft to track the designed angular velocity profile according to the mission specification［1］.In the field of on－orbit servicing（OOS）which has been commonly accepted as the capacity to support the sustained development of the space technology for a nation，the autonomous rendezvous and docking are attracting more and more attention of the space community due to the concerns of efficiency，cost and safety.Major space agencies have implemented and is implementing technological demonstration missions for autonomous satellite on－orbit servicing，which include the engineering test satellite—VII（ETS－7）launched by Japanese Aerospace Exploration Agency（JAXA）in 2007［1－3］，the orbital express program developed by Defense Advanced Research Projects A－gency（DARPA）in 2007［4－5］，the dynamics of the equatorial ionosphere over SHAR（DEOS）program sponsored by Germany Space Agency［6］，and the on－going space docking project by China Academy of Space Technology.In such testing programs，the chaser，which is the servicing spacecraft designed to conduct OOS mission，is firstly required to track and rendezvous with an on－orbit client which is the spacecraft to be serviced and then to dock with it.For the successful docking to the client，the chaser must be able to track the angular velocity of the client in the presence of dynamic uncertainties.Therefore the angular velocity tracking is considered as an indispensable ability to the spacecraft.

Since the on－orbit dynamics of spacecraft is changing due to fuel consumption，failure deployment of a component into the expected configura－tion，docking with another spacecraft，capturing of an object，payloads added or removed，or other environmental effects，all the advanced control technologies based on known dynamics cannot be applied to the problem.Some on－orbit adaptation mechanism should be integrated into the satellite controller.Researchers in space community have devoted much effort to this challenging subject.To deal with the inertia uncertainties of an on－orbit satellite，Ref.［7］derived an adaptive controller，which was an effective PI controller with an integrator，to provide asymptotic tracking of arbitrary angular velocity even without mass distribution information.The quaternion－based adaptive full－state feedback controller［8］was proposed in which the transformed tracking error dynamics were used to compensate for uncertainties in the inertia matrix and a filter motivated by the Lyapunov－like stability analysis was used to generate angular velocities from attitude measurements.Ref.［9］applied a nonlinear passivity－based adaptive control strategy to angular velocity tracking for a spacecraft with unknown inertia parameters，and pointed out that the unknown inertia parameters could be precisely identified with persistency excitation condition.A nonlinear－optimal control strategy was devised in Ref.［10］using Hamilton－Jacobi formulation to deal with the attitude tracking problem of rigid－asymmetric spacecraft.To enable a service satellite to rendezvous and dock with a tumbling satellite whose dynamics model is unknown，Liang and Ma developed a Lyapunov based adaptive control law with dynamics uncertainty compensation capacity to guarantee the asymptotical angular velocity tracking for the priordock alignment and post－docking stabilization［11］.In the research described in this paper，an adaptive angular velocity tracking law with an adaptation mechanism to the dynamics uncertainties in inertia of the spacecraft is developed based on the Lyapunov analysis.The proposed adaptation mechanism enables the controller to track any desired angular velocity trajectories even in the presence of uncertainty inertia parameters，although it does not guarantee the inertia tensor be－ing precisely identified.

2 Problem Description

The attitude dynamics of a rigid spacecraft is governed by the following Euler equation

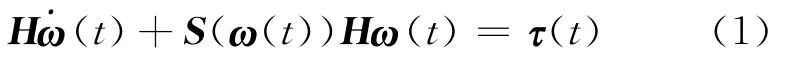
where H∈R3×3is the symmetric inertia matrix of the spacecraft given by

ω（t）＝［ω1t ω2（t） ω3（t）］T∈R3×1represents the angular velocity of the spacecraft，τ＝［τ1τ2τ3］T∈R3×1the resultant external torque caused by all attitude actuations acting on the spacecraft expressed in the spacecraft body frame，and S（ω（t））the skew symmetric cross product matrix ofω（t）given by

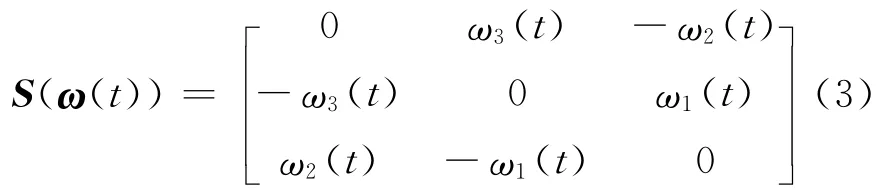
The objective of angular velocity tracking for the system described in Eq.（1）is to forceω（t）to track a desired angular velocity trajectory，ωd（t）.For this purpose，a nonnegative Lyapunov function candidate can be chosen as follows

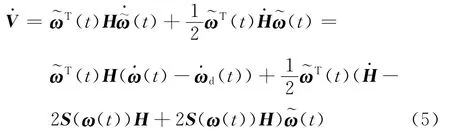
For a multibody dynamic system，the matrix－2S（ω（t）His skew symmetric，which makes（t）（－2S（ω（t））H）（t）＝0.Therefore Eq.（5）can be reduced as

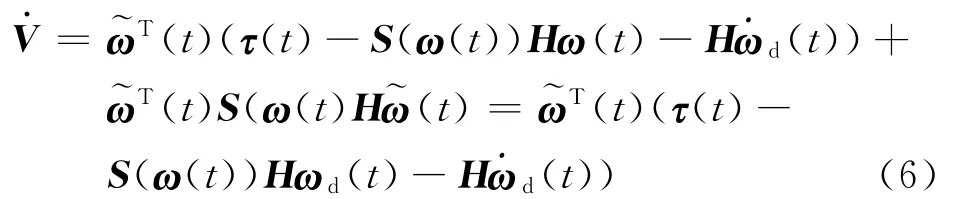
For the purpose of tracking the angular velocityωd（t），the following control law can be chosen

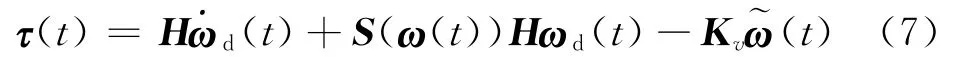
where Kvis the control gain matrix which is positive and symmetric.Substituting Eq.（7）into Eq.（6）results in the time derivative of Lyapunov function as

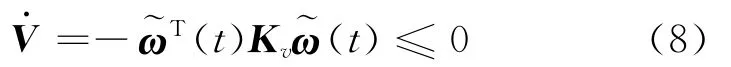
Eq.（8）means the tracking error（t）will converge exponentially to zero.In other words，it can be concluded that the control law given in Eq.（7）can guarantee the spacecraft to track any desired angular velocityωd（t）with an exactly known inertia tensor of the spacecraft.

In practice，however，it is difficult to obtain the accurate inertia tensor of an on－orbital spacecraft because its inertia parameters can change due to fuel consumption，failure deployment of a component into the expected configuration，docking with another spacecraft，capturing of an object，payloads added or removed，or other environmental effects.This fact indicates that the tracking law given in Eq.（7）can only be implemented based on an estimated inertia tensor of the spacecraft.

3 Adaptive Angular Velocity Tracking

In order to deal with the uncertainties of the spacecraft inertia parameters，some adaption mechanism should be incorporated into the tracking law given in Eq.（7）.To design such an adaptive tracking law，a nonnegative Lyapunov function candidate can be constructed as follows

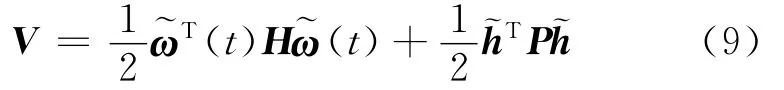
where h＝［h11h22h33h12h13h23］Tis the vector consist of the six unique elements of the inertia tensor of H，~h＝＾h－h(huán)，＾his the estimation of h，and Pis assumed to be a symmetric and positive－definite gain matrix.Differentiating the Lyapunov function given in Eq.（9）with respect to time，we can get

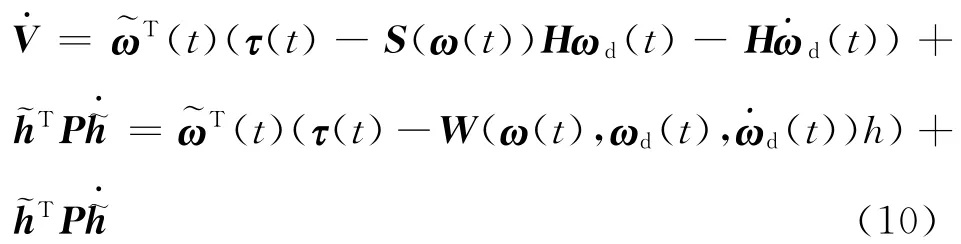
where Wis a 3×6matrix given by follows

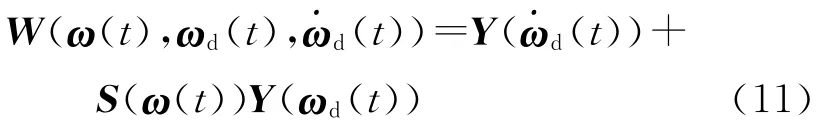
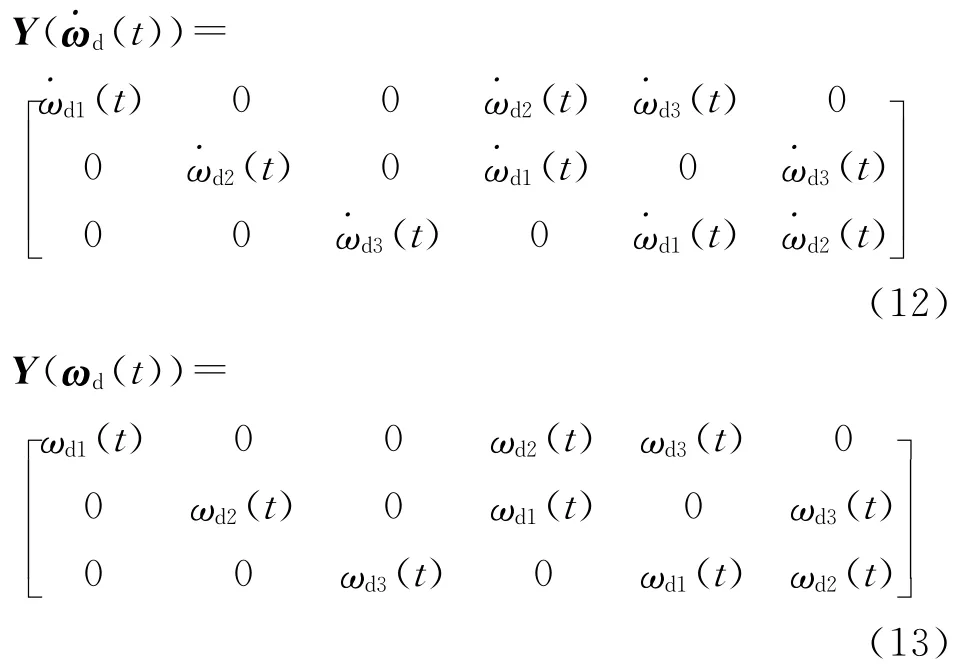
Implementing the tracking law given in Eq.（7）based on the estimated inertia tensor，we have

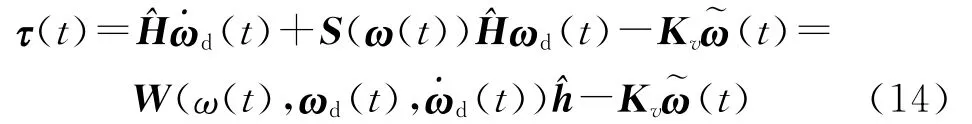
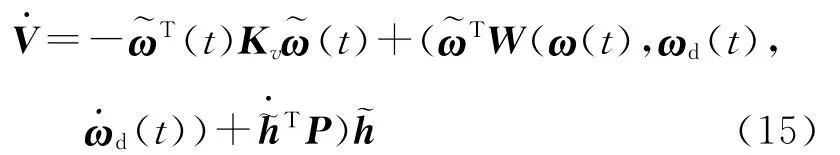
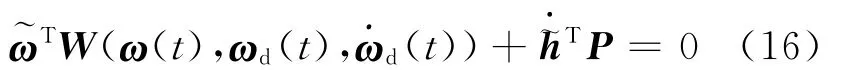
which leads to

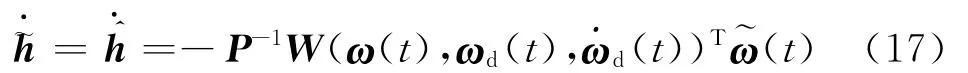
In this way，the resulting derivative of Lyapunov function will become the following

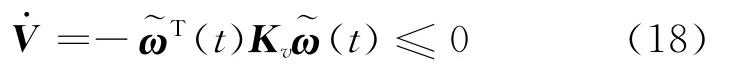
which implies that the tracking law given in Eq.（14）with the adaption law given in Eq.（17）will result in a stable closed－loop dynamics even in the presence of inertia uncertainties，and enables the spacecraft to track any prescribed angular velocity trajectory.However，－0，which is ensured by（t）－0according to Eq.（17），only in－dicates that the estimation error will converge to a constant but not necessarily zero.In other words，the adaption law given in Eq.（17）does not guarantee the unknown or uncertain inertia parameters converge to their true values.Although it is not a problem if the final concern is to make the spacecraft stably tracking a desired angular velocity profile，some conditions need to be satisfied if the inertia tensor of the spacecraft is expected to be accurately estimated.

4 Simulations and Results

To verify the angular velocity tracking scheme proposed in this paper，computer simulations are conducted on a 3Dspacecraft model which is assumed to have an inertia matrix expressed in its body fixed frame as follows

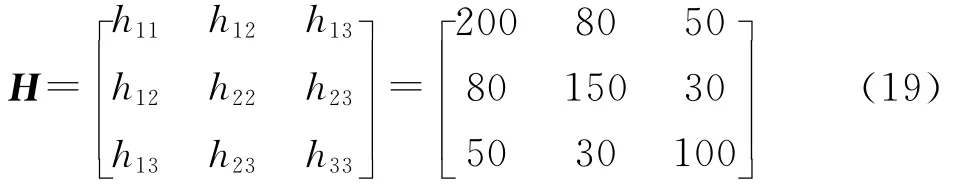
from which the vector consisting of the six unique elements of the inertia tensor can be figured out as

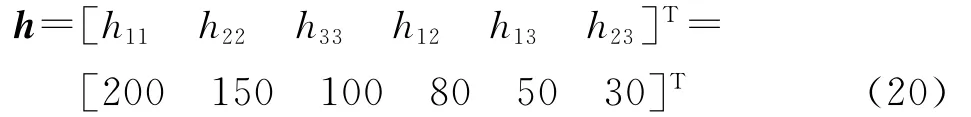
The angular velocity profile to be tracked is produced according to a simulated spacecraft out of control and its angular velocity is plotted in Fig.1.

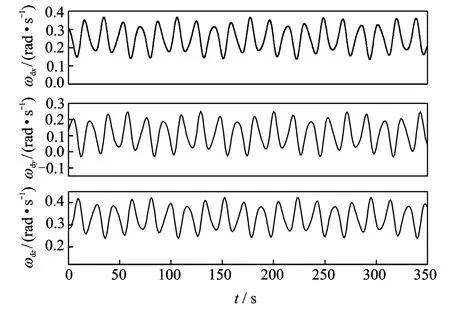
Fig.1 Angular velocity to be tracked

The angular velocity tracking simulations for both the spacecrafts with an exactly known inertia tensor and an uncertain inertia tensor are carried out and their results are described in the following parts.

4.1 Angular velocity tracking with known H

In this case，the tracking law given in Eq.（7）is applied with a control gain matrix Kv＝diag（10 10 10）.And the initial angular velocity of the spacecraft isω（0）＝［6 10 8］T（°／s）.Fig.2is the time histories of the angular velocities for the spacecraft，from which it can be found that the angular velocities of the spacecraft converge to the desired angular velocities after about 40s，and it means that the nonlinear tracking law given in Eq.（7）can control the spacecraft follow a desired angular velocity trajectories.Fig.3is the time histories of the control torques acting on the axes of the body fixed frame of the spacecraft.

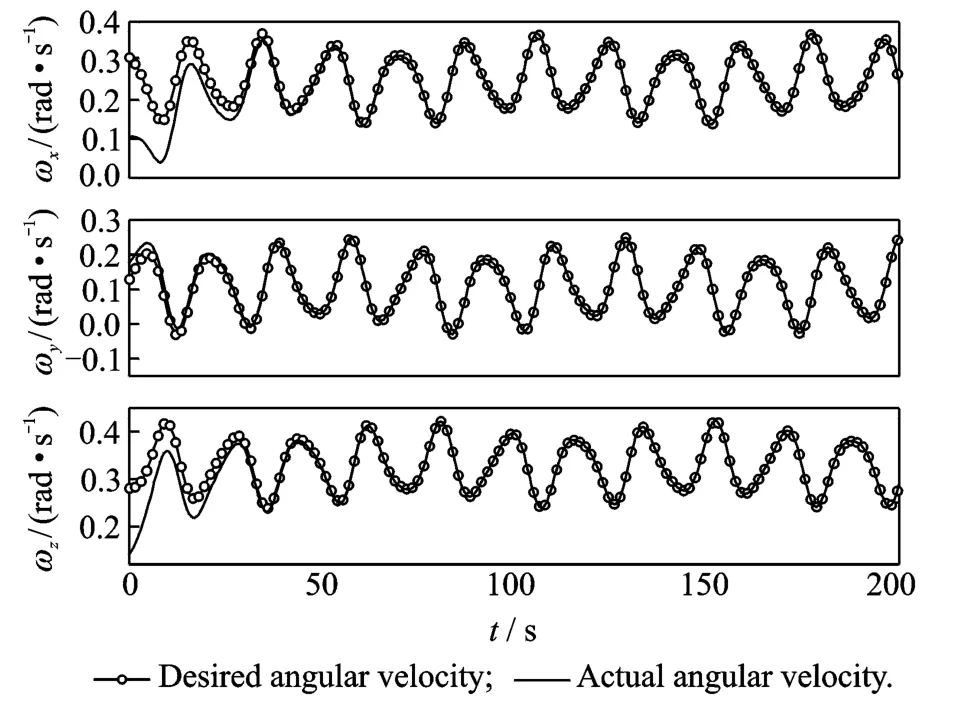
Fig.2 Time histories of angular velocities

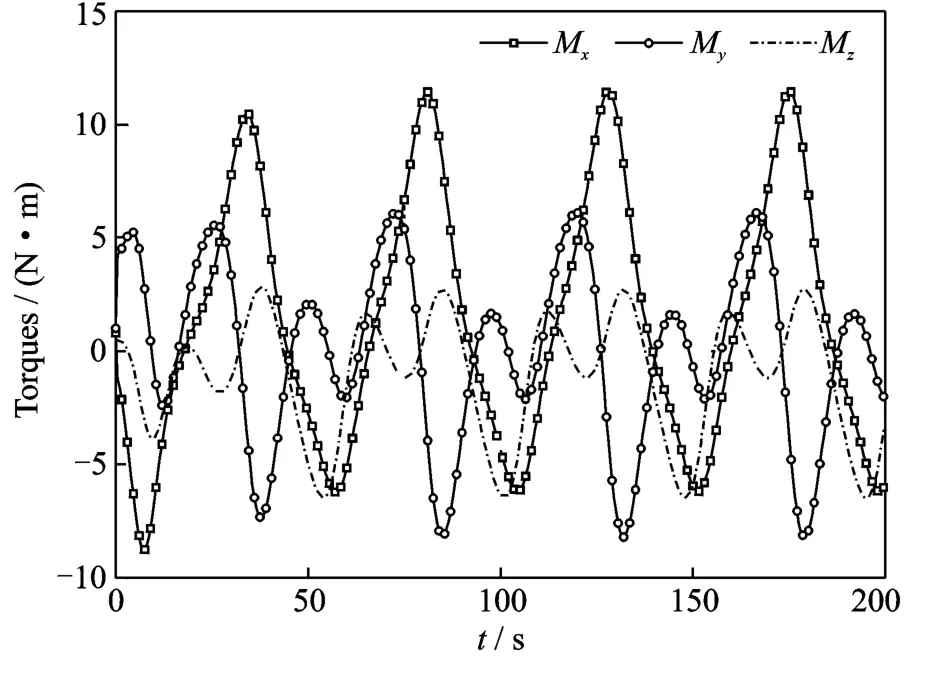
Fig.3 Time histories of control torques

4.2 Angular velocity tracking with unknown H

Suppose only an estimated inertia tensor matrix of the spacecraft is available as＾H，the six unique elements are＾h0＝ ［220 120 60 60 130 75］T（kg·m2）.The initial angular velocity isω（0）＝［6 10 8］T（°／s）.In this case，the control law given in Eq.（14），which is implemented based on the estimated inertia tensor of the spacecraft，is applied with the control gain matrix Kv＝diag（10 10 10）.To deal with the uncertainties in the inertial tensor，the adaptation mechanism of Eq.（17）is used with the gain matrix P＝diag（10－510－510－510－510－510－5）.The simulation results are illustrated in Figs.4—6.From Fig.4which displays the time histories of the angular velocity tracking of the spacecraft，we can see that the angular velocity of the spacecraft eventually converges to the desired angular velocity，which means that adaptive nonlinear control law given in Eqs.（14，17）can drive the spacecraft to follow a desired angular velocity profile.The six estimated unique elements of the inertia tensor of the spacecraft are plotted in Fig.5，which demonstrates that the uncertain inertia tensor of the spacecraft converges to a constant value in the process of control but is not its real value.This is acceptable because the main goal here is to drive the spacecraft to track a desired angular velocity profile as opposed to precisely identify the true value of the spacecraft inertia tensor.In other words，the adaptive nonlinear control law given in Eqs.（14，17）can make the spacecraft stably tracking a desired angular velocity profile though it does not guarantee the unknown or uncertain inertia parameters converge to their true values.The time histories of the control torques acting on the spacecraft are depicted in Fig.6.

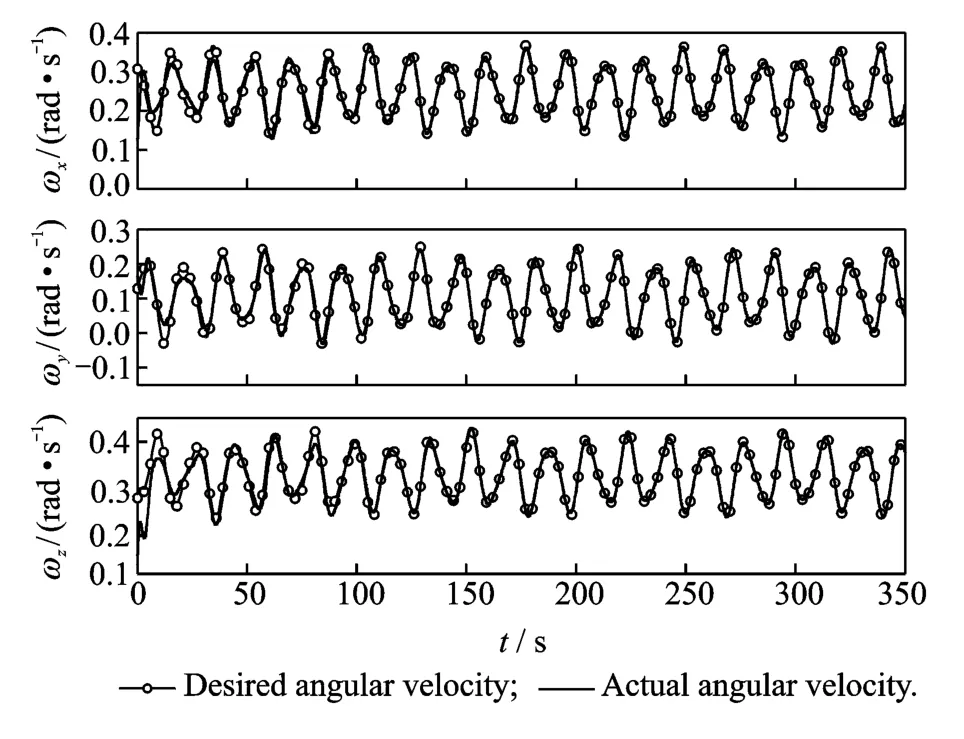
Fig.4 Actual and reference angular velocities

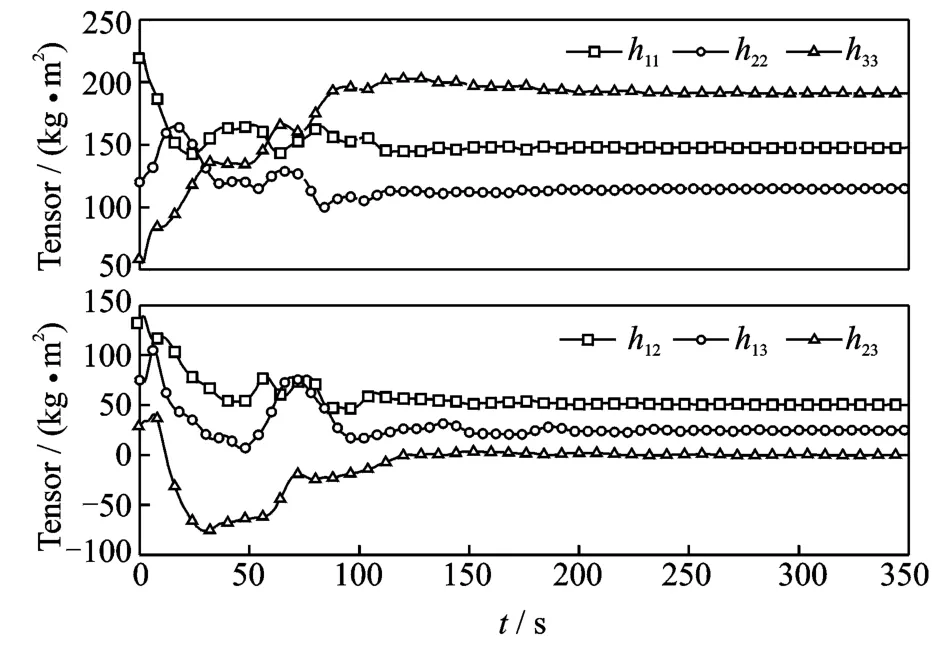
Fig.5 Time history of six estimated unique elements of inertia tensor of spacecraft

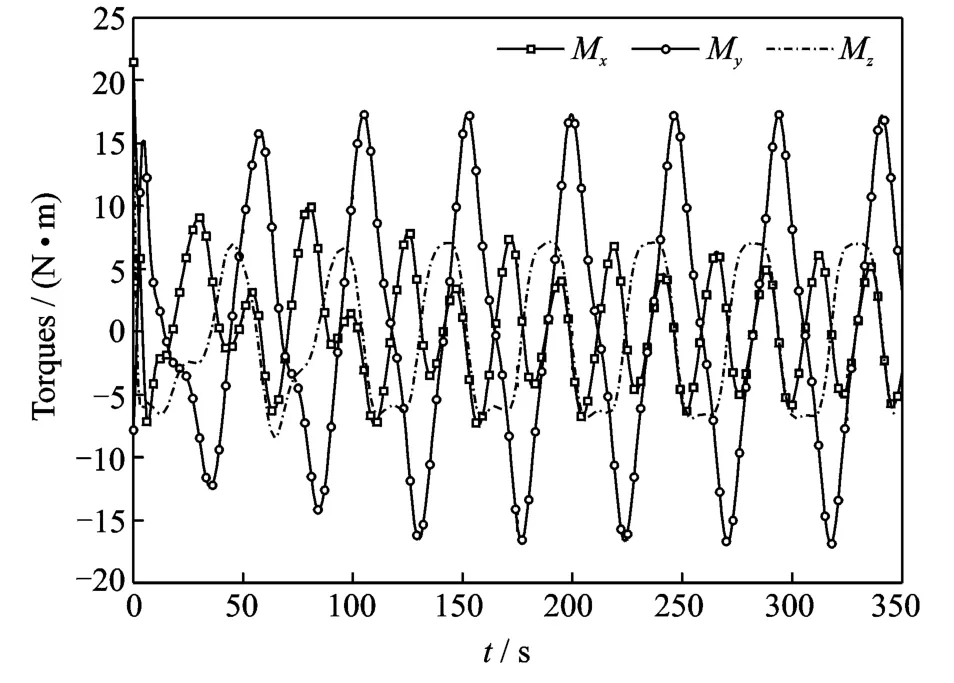
Fig.6 Time history of torque of spacecraft

5 Conclusions

This paper proposes an adaptive nonlinear control algorithm for the angular velocity tracking of spacecraft with dynamic uncertainties.With such an adaptive control method，the spacecraft can be controlled to track any arbitrary angular velocity trajectory even in the presence of uncertainties in inertia tensor so that the spacecraft can fly with no relative angular velocity to the target spacecraft or other objects to be served，which makes it possible for the spacecraft to conduct the subsequent operations such as docking，capturing or other on－orbit manipulation.Based on the assumption that the attitude dynamics of the spacecraft is precisely known，an angular velocity feedback tracking algorithm is firstly developed and the global tracking convergence of the control algorithm is proved through the Lyapunov analysis.To deal with the dynamic uncertainties of the spacecraft in its inertia tensor，a nonlinear adaptation mechanism is then designed based on Lyapunov method.With such an adaptation mechanism the spacecraft can track any desired angular velocity trajectories even an available uncertain inertia tensor.The analysis also shows that the adaptation mechanism does not guarantee the inertia tensor being precisely identified.Computer simulations on a 3Dspacecraft are carried out to verify the effectiveness of the proposed adaptive control policy and the simulation results demonstrate that the proposed adaptive control policy has good angular velocity tracking performance.

［1］ Oda M.Experiences and lessons learned from the ETS－VI1robot satellite［C］／／Proceedings of the 2000IEEE International Conference on Robotics a Automation.San Francisco，CA：IEEE，2000：914－919.

［2］ Oda M，Kawano S，Kibe K，et al.ETS－7，a rendezvous docking and space robot technology experiment satellite result of the engineering model development work［C］／／Proceedings of the 34th SICE Annual Conference.Hokkaido，Japan：IEEE，1995：1627－1632.

［3］ Kasai T，Oda M，Suzuki T.Results of the ETS－7 mission—Rendezvous docking and space robotics experiment［C］／／Proceedings of the 5th International Symposium on Artificial Intelligence，Robotics and Automation in Space.Nordwijk，Netherlands：ESTEC／ESA，1999：299－306.

［4］ Whelan D A，Adler E A，Wilson S B，et al.DARPA orbital express program：Effecting a revolution in space－based systems［C］／／International Symposium on Optical Science and Technology，International Socity for Optics and Photonics.San Diego，CA：［s.n.］，2000：48－56.

［5］ Seth D P.Orbital express：Leading the way to a new space architecture［C］／／Space Core Technology Conference.Colorado：［s.n.］，2002：19－21.

［6］ Rupp T，Boge T，Kiehling R，et al.Flight dynamics challenges of the German on－orbit servicing mission DEOS［C］／／Proceedings of the 21st International Symposium on Space Flight Dynamics.Toulouse，F(xiàn)rance：［s.n.］，2009：1－13.

［7］ Sanyal A K，Chellappa M，et al.Globally convergent adaptive tracking of spacecraft angular velocity with inertia identification and adaptive linearization［C］／／Pmceedings of the 42th IEEE Conference on Decision and Control.Maui，Hawaii，USA：IEEE，2003：2704－2709.

［8］ Costic B T，Damon D M，Queiroz M S，et al.A quaternion－based adaptive attitude tracking controller without velocity measurements［C］／／Proceedings of the 39th IEEE Conference on Decision and Control.Sydney，Australia：IEEE，2000：2424－2429.

［9］ Thienel J K.Estimation of spacecraft inertia parameters［C］／／AIAA Guidance，Navigation and Control Conference and Exhibit.Honolulu，Hawaii：AIAA，2008：1－8.

［10］Sharma R，Tewari A.Optimal nonlinear tracking of spacecraft attitude maneuvers［J］.IEEE Transactions on Control System Technology，2004，12（5）：677－682.

［11］Liang J，Ma O.Angular velocity tracking for satellite rendezvous and docking［J］.Acta Astronautica，2011，69（11）：1019－1028.