大位移水平井段巖屑運移實驗研究

相恒富 孫寶江 李 昊 牛洪波

（1.中國石油大學（華東），山東青島 266580；2.中石化勝利石油管理局鉆井工藝研究院，山東東營 257017）

大位移水平井由于具有較長的水平段位移，鉆具極易沉向井眼低邊，且鉆井液流向與重力方向垂直，導致井筒低邊易于形成巖屑沉積床。巖屑床的存在，導致環(huán)空內壁形成鍵槽、黏附卡鉆等問題，降低了鉆井效率，提高了鉆井成本［1］。確保井眼環(huán)空清潔是貫穿整個水平井鉆井過程的關鍵問題。傳統(tǒng)的水力參數(shù)設計理論，一般不考慮巖屑運移的影響，這在直井、井深不大的定向井和水平井應用時不會產(chǎn)生較大誤差，但在應用于大位移井時，由于斜井段和水平段很長，如果不考慮巖屑運移（巖屑床）的影響，將會產(chǎn)生較大誤差，同時過高的巖屑床也會帶來許多安全問題。另外，大位移井由于井深，循環(huán)壓耗大，受設備能力的限制，其水力參數(shù)的計算必須更加精確，水力參數(shù)的設計也會更加復雜，需要考慮的因素也會更多。

為了獲取大位移水平井巖屑床厚度與巖屑運移影響參數(shù)的關系，國內外學者進行了大量的實驗研究，獲得了一些經(jīng)驗性的模型和認識。Tulsa大學的Larsen在直井巖屑沉降速度基礎上，利用實驗求得修正系數(shù)，導出了適用于55～90°的定向井巖屑運移最小返速模型［2］。N. Malekzadeh［3］在 Larsen 模型基礎上，借助計算機迭代算法獲得了井斜角0～90°時井眼清潔最小環(huán)空排量預測方法，但是，由于鉆頭水馬力和允許的鉆井液循環(huán)當量密度ECD限制，很多時候達不到最小攜巖排量的要求，故水平井攜巖需考慮巖屑運移的影響。汪海閣等［4］通過大量室內實驗，得到了水平井段巖屑運移規(guī)律，采用多元參數(shù)統(tǒng)計方法回歸實驗數(shù)據(jù)，得到了水平井段環(huán)空巖屑床厚度的經(jīng)驗模型，但是該模型忽略了對巖屑運移有重要影響的巖屑粒徑、井斜角及井眼尺寸等因素的影響。Ozbayoglu等［5］應用量綱分析法，通過大量實驗回歸出無因次巖屑床面積模型，但模型并不包含井斜角、鉆桿旋轉和巖屑粒徑的影響。筆者在已有實驗和理論研究基礎上，重點考慮鉆桿轉速及偏心度、井斜角、巖屑粒徑和井眼尺寸對水平井巖屑運移的影響，建立了大位移水平井穩(wěn)態(tài)無因次巖屑床厚度方程。

1 大位移水平井巖屑運移實驗裝置設計

實驗研究目的是獲取鉆井液環(huán)空流速、鉆井液密度、鉆井液流變性（有效黏度、動切力、動塑比）、鉆桿轉速、鉆桿偏心度、巖屑粒徑、井斜角與環(huán)空巖屑濃度、巖屑床厚度的關系，獲取巖屑運移特征，修正攜巖判據(jù)。依據(jù)巖屑運移機理設計的水平井攜巖實驗裝置見圖1，整個系統(tǒng)由鉆井液循環(huán)系統(tǒng)、加砂系統(tǒng)、鉆桿旋轉及偏心系統(tǒng)、起升系統(tǒng)、巖屑分離系統(tǒng)及控制系統(tǒng)組成。

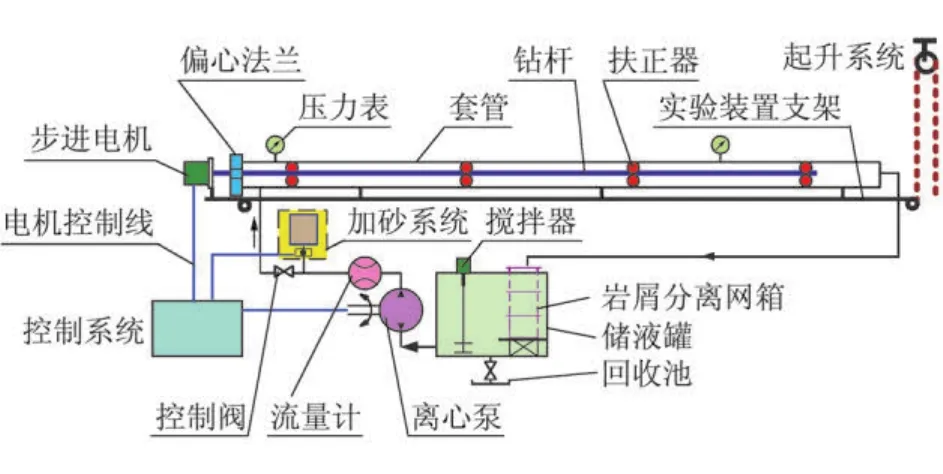
圖1 大位移水平井攜巖實驗裝置示意圖

水平井攜巖問題是復雜的固液兩相流問題，僅靠理論分析進行求解存在許多困難，模型實驗和量綱分析就是解決復雜問題的有效途徑。相似原理是進行固液多相流力學模型實驗的基礎，在滿足幾何相似的前提下，動力相似是實現(xiàn)流動相似的必要條件，即要求模型和原型中作用在巖屑上的各種力都成比例，用數(shù)學式可以表達為

式中，Ne為牛頓數(shù)，表示某種外力（可以是任何類型的力）與流體慣性力的比值；下標p和m分別表示是原型和模型的物理量，這就是實現(xiàn)流動動力相似的牛頓相似準則。

巖屑顆粒受重力、浮力、拖曳力、上舉力、塑性力、粒間離散力、相鄰巖屑支撐力以及鉆桿旋轉力綜合作用下，在環(huán)空形成懸浮層、推移層和巖屑床層3層運移形態(tài)。其中在巖屑運移方向上，起決定作用的力為拖曳力；在巖屑沉降方向上，起決定作用的力是上舉力、重力和浮力在垂直方向上的合力。但實際上，模型與現(xiàn)場設備滿足完全相似是很難實現(xiàn)的。因此，為使問題簡化，只考慮起主要作用的一種力，使其滿足牛頓數(shù)相等要求，而將其他一些次要的力忽略不計。這樣得到的結果是一種近似的動力相似，稱為局部相似。通過理論可以證明，顆粒在巖屑運移方向上的主要作用力，滿足顆粒雷諾數(shù)相似。已知顆粒雷諾數(shù)方程為

式中，ρ為鉆井液密度，kg/m3；v為巖屑與流體相對運移速度，m/s；d為巖屑當量直徑，m；μ為鉆井液有效黏度，Pa·s。由顆粒雷諾數(shù)相似可得

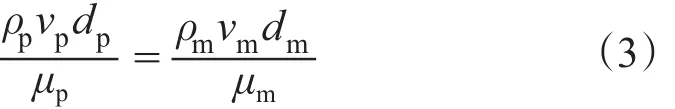
假設原型與模型用同樣的鉆井液，則ρp=ρm，那么

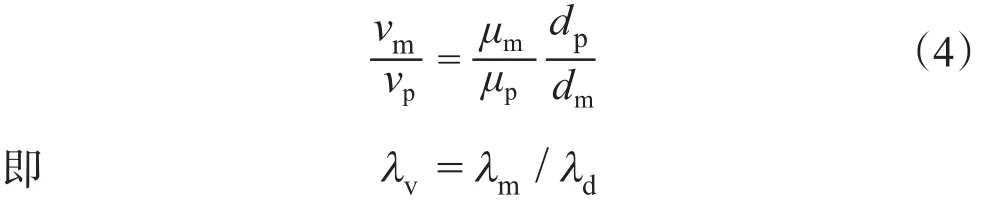
鉆井液有效黏度方程為

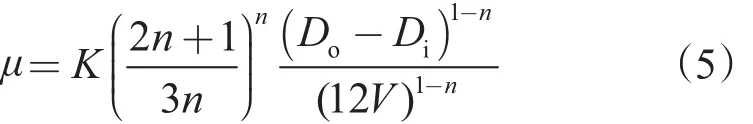
式中，K為稠度系數(shù)，Pa·sn；n為鉆井液流性指數(shù)，無因次；Do為井眼內徑，m；Di為鉆桿外徑， m；V為環(huán)空返速， m/s。

顯然，模型與原型的K、n相等，設Do、 Di按照幾何相似取值，模型與原型之比為λl，取模型與原型環(huán)空返速相同，則

由于水平井攜巖顆粒雷諾數(shù)一般滿足10＜Rep＜100［2］，則

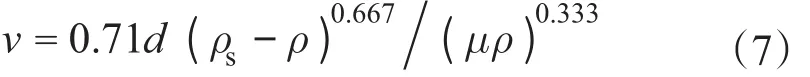
若取巖屑密度與原型一致，則

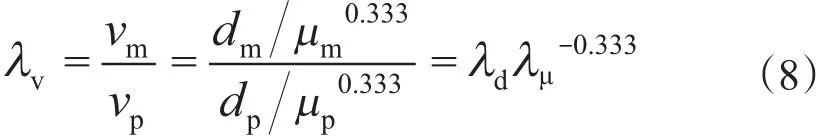
聯(lián)立式（4）、（6）、（8）有

設井眼內徑原型尺寸為139.7 mm，實驗井筒內徑為50.8 mm，則幾何相似比λl=50.8/139.7=0.364，鉆桿原型尺寸為73.9 mm，則根據(jù)幾何相似模型鉆桿外徑為26.5 mm，選取外徑25.4 mm、長度12 m的PPR管作為鉆桿。至此，大位移水平井攜巖實驗裝置的井眼尺寸和鉆桿尺寸均已得到。在環(huán)空井眼中，巖屑顆粒滿足顆粒雷諾數(shù)相似，模型中鉆井液密度、流性指數(shù)、稠度系數(shù)、巖屑密度和環(huán)空返速均與現(xiàn)場實際相同。

2 大位移水平井巖屑運移實驗及結果分析

2.1 實驗方案設計

實驗選取1～3 mm系列的石英砂模擬巖屑，密度為2.6 g/cm3；選用PAC-LV、XC、重晶石加水混合，配制4種系列的聚合物鉆井液，鉆井液流變性通過六速黏度計測量（表1）。

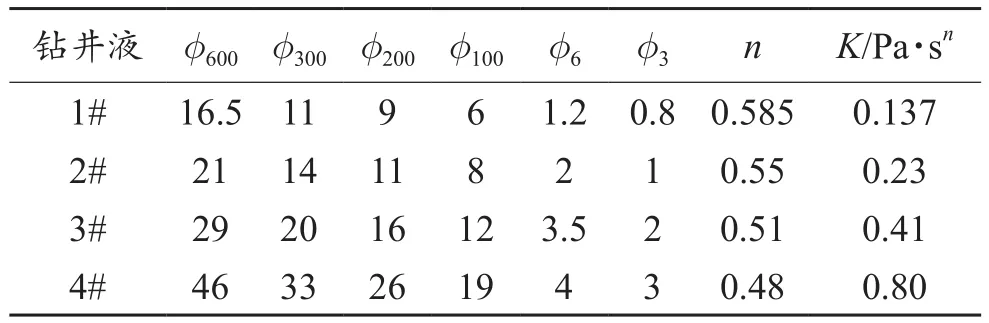
表1 實驗用鉆井液體系性能

實驗方案設計：環(huán)空返速取0.7～1.2 m/s，包含了層流和紊流2種狀態(tài)，鉆具轉速取0～120 r/m in，鉆桿偏心度分別取0、0.5、0.75，巖屑粒徑選取1～5 mm范圍，鉆進速度取10～50 m/h，鉆井液密度選取1～1.4 g/cm3。組合不同參數(shù)的取值確定實驗方案，完成了300多組實驗。

2.2 實驗結果分析

實驗將對環(huán)空返速、鉆桿轉速及偏心度、機械鉆速、井斜角、巖屑粒徑及鉆井液有效黏度對無因次巖屑床厚度的影響進行研究，以獲得無因次巖屑床厚度的回歸模型。考慮到井眼直徑不同，對水平井鉆井安全允許的巖屑床厚度要求不一樣，本文用無因次巖屑床厚度（巖屑床厚度/井眼內徑×100%）作為攜巖判據(jù)。

2.2.1 環(huán)空返速的影響 圖2為4種鉆井液下環(huán)空返速與無因次巖屑床的關系曲線，圖中點為實驗數(shù)據(jù)，曲線為實驗數(shù)據(jù)的逼近，其中巖屑選擇直徑3 mm的石英砂，鉆井液密度為1.0 g/cm3，鉆進速度45 m/h，環(huán)空平均偏心度0.5，井斜角90°，鉆桿轉速120 r/m in。由圖2可知，隨著環(huán)空返速的增加，無因次巖屑床厚度下降很快，這是因為環(huán)空返速增加，增大了環(huán)空鉆井液的紊流度，紊流的脈動特點和漩渦對形成的巖屑床有一種破壞作用；紊流的速度分布比較均勻、無尖峰，巖屑床表面的流體流速較快。鉆井液對巖屑床厚度的影響在低返速下顯著，在高返速下不明顯。

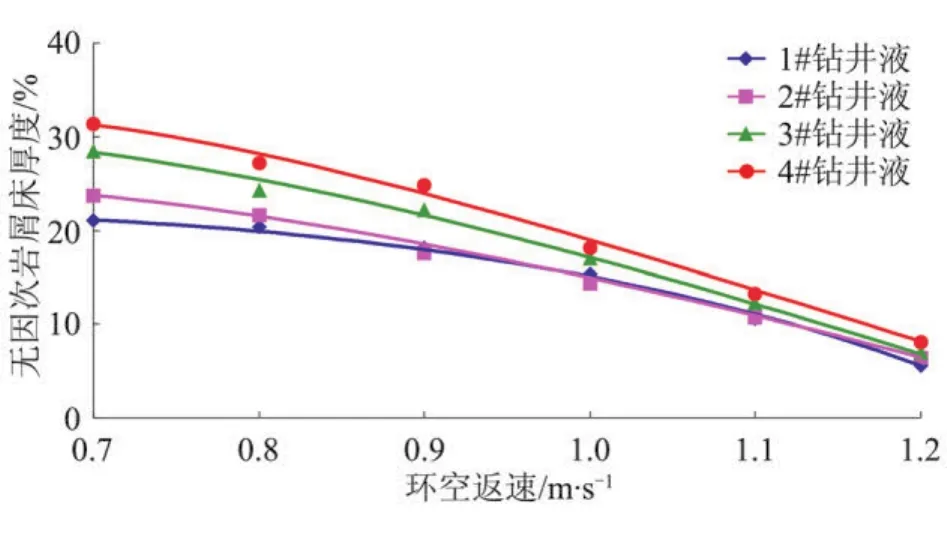
圖2 不同鉆井液時環(huán)空返速與無因次巖屑床厚度的關系

2.2.2 鉆桿轉速的影響 鉆桿轉速對巖屑床厚度的影響見圖3，可以看出，鉆桿轉速對巖屑床厚度的影響非常明顯，并且在大約20 r/m in轉速時存在一個明顯的拐點，小于20 r/m in時，下降趨勢特別大，大于20 r/m in時下降趨勢變緩。

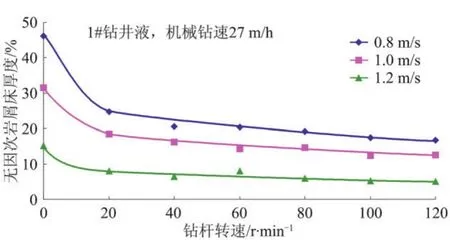
圖3 不同環(huán)空返速下鉆桿轉速與無因次巖屑床厚度的關系

2.2.3 鉆桿偏心度對巖屑床厚度的影響 在大斜度井及水平井鉆進中，由于重力下沉作用，鉆具極易躺在井眼的下側，形成偏心環(huán)空，給井眼的清洗帶來很大的困難。圖4表明，隨鉆具偏心度增大，無因次巖屑床厚度大大增加。造成這種現(xiàn)象的原因在于偏心造成環(huán)空中鉆井液返速分布不均勻，環(huán)空下部窄間隙處返速小，攜巖能力弱，環(huán)空上部寬間隙處返速大，攜巖能力強，但是由于重力作用，巖屑易于聚集到環(huán)空下部，故偏心度越大，攜巖能力越弱，巖屑床厚度越高。

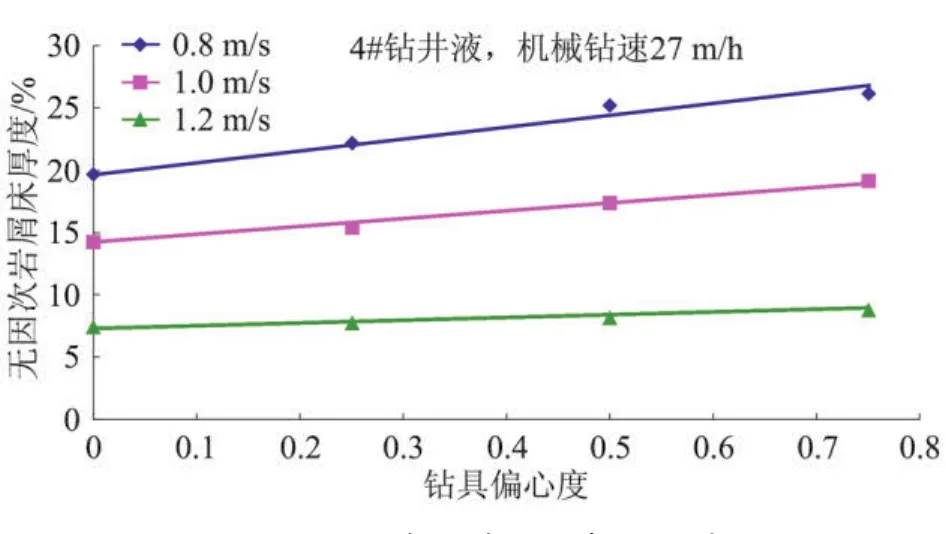
圖4 不同環(huán)空返速下鉆桿偏心度與無因次巖屑床厚度的關系

2.2.4 機械鉆速的影響 研究水平井攜巖判據(jù)的目的是保證安全鉆井和提高鉆井效率，而反映鉆井效率的參數(shù)為機械鉆速。圖5為不同環(huán)空返速下機械鉆速與無因次巖屑床厚度的影響曲線，采用3#鉆井液，巖屑選擇直徑3 mm的石英砂，鉆井液密度1.0 g/cm3，環(huán)空平均偏心度0.5，井斜角90°，鉆桿轉速120 r/min。由圖可知，隨著鉆進速度增大，巖屑床厚度增大，在環(huán)空返速小時，巖屑床厚度增大趨勢明顯，環(huán)空返速大時，增大趨勢變緩。

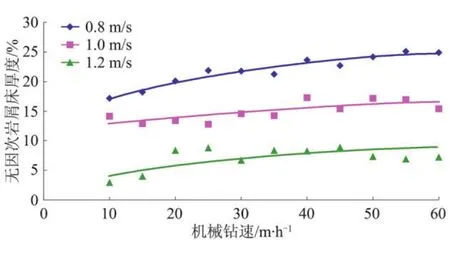
圖5 不同環(huán)空返速下機械鉆速與無因次巖屑床厚度的關系

2.2.5 井斜角的影響 選2#鉆井液，平均偏心度0.5，鉆桿轉速120 r/m in，鉆進速度46 m/h，巖屑粒徑3 mm，鉆井液密度1.0 g/cm3，得到井斜角與無因次巖屑床厚度的關系曲線（圖6），可以看出，井斜角在50～90°范圍有個拐點，約在65°左右，此處巖屑床高度最大，成為最難攜巖井段，原因在于此處易造成巖屑床下滑，之后隨井斜角增大，巖屑床高度緩慢降低，這與理論分析的結果吻合。

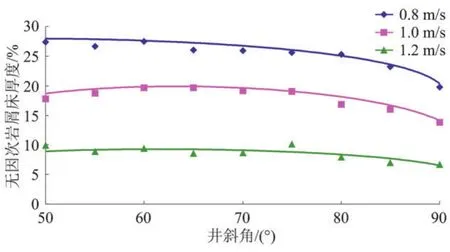
圖6 不同環(huán)空返速下井斜角與無因次巖屑床厚度的關系

2.2.6 巖屑粒徑的影響 巖屑粒徑對巖屑的運移影響也較大（圖7），而巖屑粒徑的大小同鉆頭類型、巖石類型、鉆壓、鉆桿轉速及巖屑運移效率密切相關。在實驗所選取的粒徑范圍內，小尺寸巖屑比大尺寸巖屑更難運移，因為小尺寸巖屑更易聚集，顆粒間作用力更大。

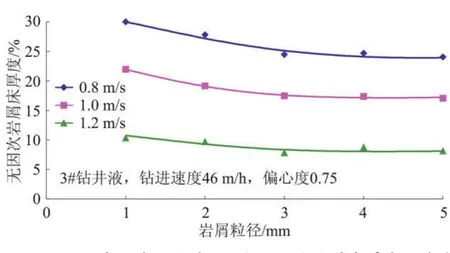
圖7 不同環(huán)空返速下巖屑粒徑與無因次巖屑床厚度的關系

2.2.7 鉆井液有效黏度的影響 鉆井液流變性能是影響水平井鉆井液攜巖效果極為重要的因素，也是一種主要的可控因素。在水平井中，鉆井液有效黏度對巖屑床厚度影響見圖8，可以看出，低黏度鉆井液對環(huán)空攜巖效果更佳，其原因在于，在水平井和大斜度井中，紊流攜巖效果更佳，低黏度流體易于在環(huán)空獲得紊流流態(tài)。

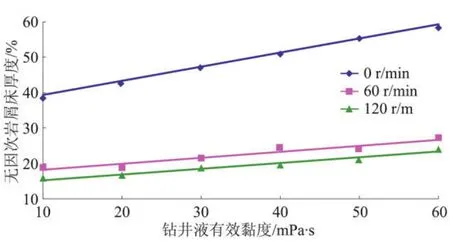
圖8 不同轉速下鉆井液有效黏度與無因次巖屑床厚度的關系

2.2.8 井眼尺寸的影響 鉆井實踐表明，井眼尺寸對巖屑運移也有明顯影響，根據(jù)文獻資料，得到了127 mm、216 mm和311 mm井眼巖屑運移規(guī)律（圖9）。

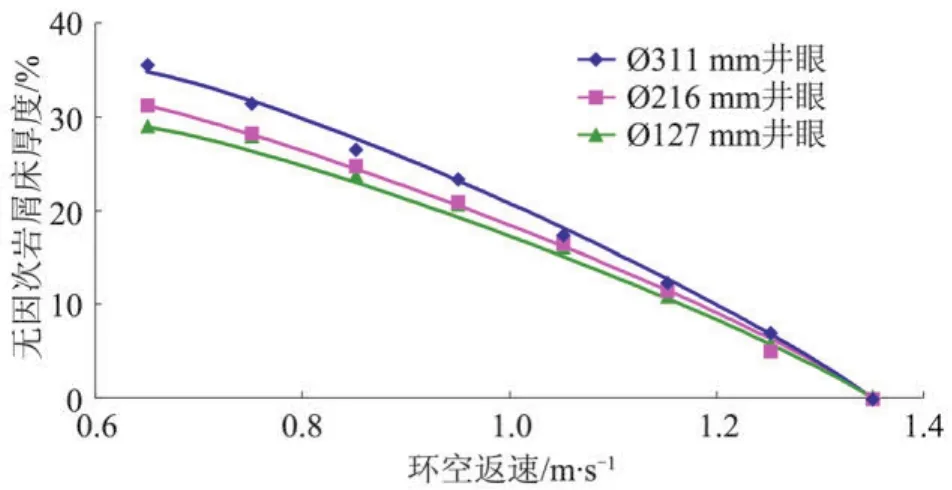
圖9 井眼尺寸與無因次巖屑床厚度的關系

3 巖屑運移模型推導

在實驗分析的基礎上，利用matlab軟件，采用非線性回歸方法獲得大位移水平井穩(wěn)態(tài)無因次巖屑床厚度方程

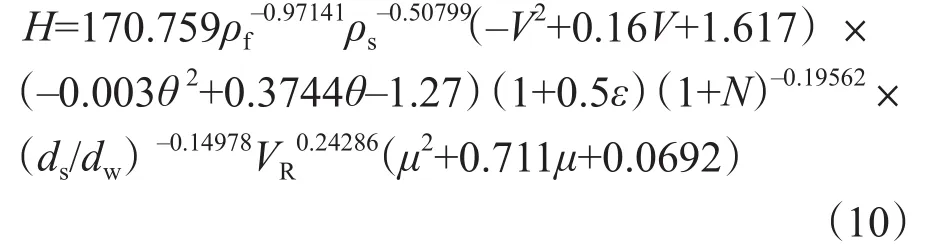
式中，H為無因次巖屑床厚度，%；V為環(huán)空返速，m/s；N為鉆桿轉速，r/m in；ε為鉆桿偏心度；ρf為鉆井液密度，g/cm3；ρs為巖屑密度，g/cm3；VR為鉆進速度，m/s；μ 為有效黏度，Pa·s；Do、Di、ds為井眼內徑、鉆桿外徑、巖屑粒徑，m；θ為井斜角，°；dw為環(huán)空間隙，dw=Do–Di。

冪律流體有效黏度使用式（5）計算，賓漢流體有效黏度使用下式計算

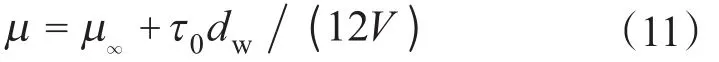
式中，μ∞為賓漢流體塑性黏度，Pa·s；τ0為賓漢流體動切力，Pa。

4 回歸模型驗證

水平井巖屑床厚度常用汪海閣公式［4］，但是與本文公式相比，汪海閣回歸公式不含井眼尺寸、巖屑粒徑、井斜角對無因次巖屑床厚度的影響，限制了其應用范圍。

為了驗證本文公式（10）的可靠性，與汪海閣公式進行了對比，計算時取文獻［4］所用的實驗條件，即井眼內徑127 mm，鉆桿外徑76.2 mm，偏心度取0.5，鉆桿轉速 120 r/m in，鉆井液有效黏度 40 mPa·s，巖屑粒徑3.4 mm，井斜角90°，鉆井液密度1.05 g/cm3， 巖屑密度2.6 g/cm3，計算結果見圖10。可以看出，兩者基本吻合，但也有一些差異，汪海閣回歸公式基本為一直線，而本研究公式則為一拋物線，因為本研究考慮了井斜角、巖屑粒徑及井眼尺寸對無因次巖屑床厚度的影響。

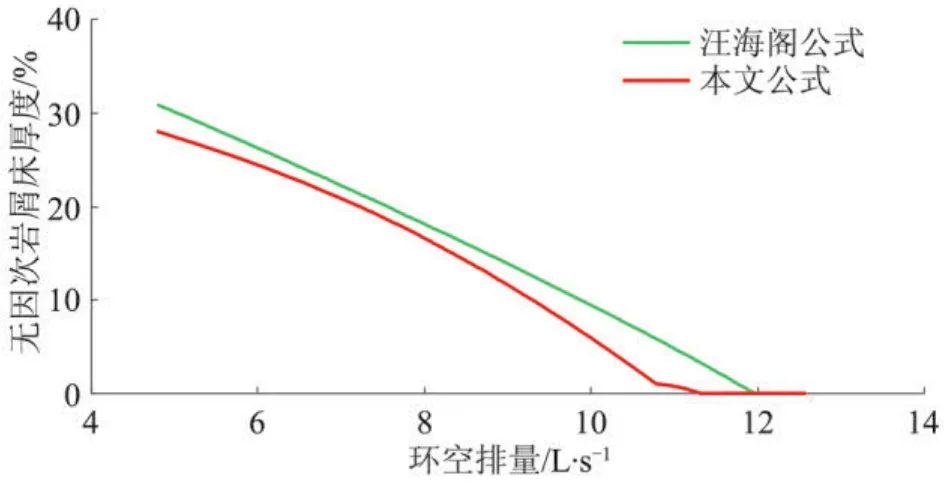
圖10 本模型與汪海閣公式對比

選取勝利油田樊154-平1井進行實例計算。該井套管內徑152.4 mm，鉆桿外徑88.9 mm，水平井段2 856～4 066 m，井斜角從 87.39°變化到 89.9°。其鉆井參數(shù)為：排量13 L/s，偏心度0.5，鉆桿轉速120 r/m in，其他參數(shù)見表2。通過表2數(shù)據(jù)對比發(fā)現(xiàn)，根據(jù)實測數(shù)據(jù)計算得到的9趟10個井段點最小排量（無因次巖屑床厚度10%時對應的排量）均小于實際排量，是安全的；通過計算循環(huán)壓耗與泵壓對比，發(fā)現(xiàn)循環(huán)壓耗與給定的泵壓相差很小，說明本方法能夠滿足現(xiàn)場施工的需要。

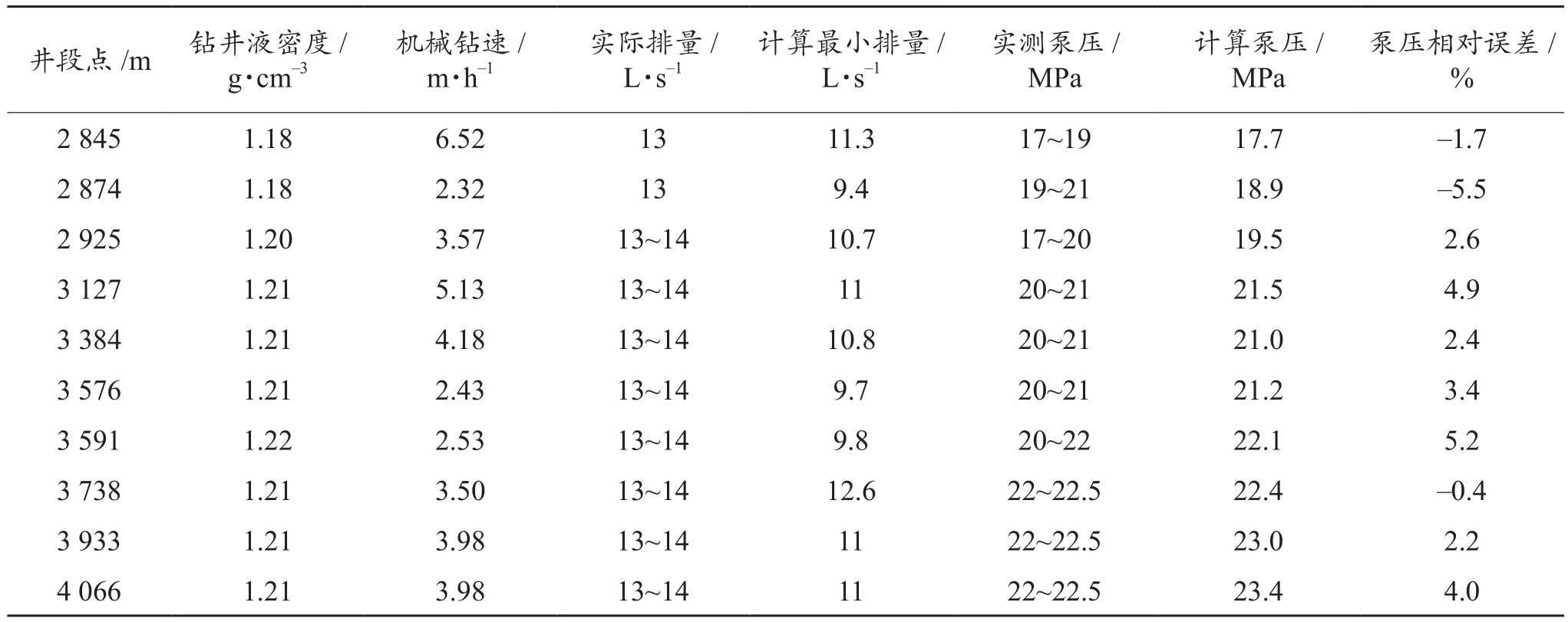
表2 水平井段10個井段點的鉆井參數(shù)及實測數(shù)據(jù)與計算數(shù)據(jù)對比

5 結論

（1）以顆粒雷諾數(shù)對水平井攜巖實驗裝置進行了相似系統(tǒng)設計，獲得了實驗裝置與原型的相似關系公式，模型與原型鉆井液密度、流性指數(shù)和稠度系數(shù)、巖屑密度、環(huán)空返速相同的條件下，巖屑粒徑相似比與幾何相似比和鉆井液流性指數(shù)有關。

（2）進行了大位移水平井攜巖實驗，獲取了不同攜巖參數(shù)與無因次巖屑床厚度的關系。

（3）根據(jù)實驗分析結果建立了大位移水平井穩(wěn)態(tài)無因次巖屑床厚度方程，該方程能夠反映環(huán)空返速、鉆井液密度及有效黏度、巖屑密度及粒徑大小、鉆桿轉速及偏心度、井斜角、機械鉆速和井眼尺寸等10個參數(shù)與無因次巖屑床厚度的關系，與現(xiàn)有模型相比，該模型能反映井斜角、井眼尺寸、巖屑粒徑的影響，應用范圍更廣，計算結果更精確，在保證井眼凈化前提下，可以優(yōu)化機械鉆速。

［1］ 張景富，俞慶森，嚴世才.側鉆井鉆井液攜屑能力試驗研究［J］.石油鉆采工藝， 2000， 22（2）：12-16.

［2］ LARSEN T I, PELEHVARI A A, AZAR J J. Development of a new cuttings transport model for high-angle wellbores including parameters［J］. SPE Drilling and Completion,1997, 12（2）: 129-136.

［3］ MALEKZADEH N, MOHAMMADSALEHI M. Hole cleaning optimaization in horizontal wells, a new method to com pensate negative hole inclination effects［R］.SPE 143676, 2011.

［4］ 汪海閣，劉希圣，丁崗.水平井段巖屑床厚度模式的建立［J］. 石油大學學報：自然科學版，1993， 17（3）：25-31.

［5］ OZBAYOGLU M E, SAASEN A, SORGUN M, et al.Effect of pipe rotation on hole cleaning for water-based drilling fluids in horizontal and deviated wells［R］. SPE 114965, 2008.

［6］ 姜洪閣. 鉆具旋轉對巖屑運移的影響規(guī)律研究［J］.內蒙古石油化工，2011（19）：139-142.

［7］ SALAZAR-MENDOZA, R, GARCIA-GUTIERREZ A. A two-region hydraulic averaging model for cuttings transport during horizontal well drilling［J］. Journal of Canadian Petroleum Technology, 2008, 47（3）: 55-61.

［8］ 郭曉樂，汪志明，龍芝輝. 大位移鉆井全井段巖屑動態(tài)運移規(guī)律［J］. 中國石油大學學報：自然科學版，2011，35 （1）：72-76.