解析有限開區間上單變量函數的一致連續
蔣 品 彭鎮靜 賈桂麗
(1.虞城縣高級中學,河南 虞城 476300;2.商丘學院,河南 商丘 476000)
討論有限開區間上單變量函數的一致連續,對數學分析的研究和學習,有很重要的意義。而單變量函數的一致連續對多變量函數的一直連續有重要的理論指導意義[1]。本文在有限閉區間上探討。
定義:設 f是 X 上的單變量函數.若?ε>0,?δ>0,使得當 x1,x2∈X,f(x1)-f(x2)<ε時總成立,則稱f是X上的一致連續函數[2]。顯然,若f是X上的一致連續函數,則f一定是X上的連續函數(反之通常不正確)。
作一個管子如圖1,存在這樣的一個管子,可以在一致連續函數曲線上平行移動。
下面是一致連續的三個重要的命題,分別是不一致連續的定義,一致連續的柯西定義和一致連續在開區間的一個重要命題.
命題1 (不一致連續的充要條件)X上的單變量函數f不一致連續??ε>0和{xn},{yn}?X使得(xn-yn)=0,并且 f(xn)-f(yn)≥ε 任意n∈N+。

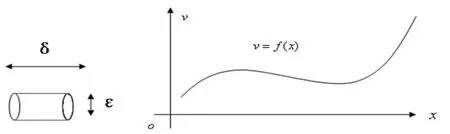
圖1
必要性 假定?ε>0和 {xn},{yn}?X,使得(xn-yn)=0, 并且≥ε,?n∈N+這 時,?ε>0,?xN,yN∈X, xN-yN<δ使 得≥ε.這說明f不是X上的一致連續函數.
命題2 若f是區間I上的一致連續函數,δ0>0是常數,則必存在M>0使得當x,y∈I,x-y ≤δ0時總成立 f(x)-f(y)≤M.

命題3 有限開區間(a,b)上的連續函數一致連續?存在有限單側極限 f(a+0)和 f(b-0).
證明 充分性 若f是(a,b)上的一致連續函數,即?ε>0,?δ>0,使得當 x,y∈(a,b),x-y <2δ時成立 f(x)-f(y) <ε,則當 x,y∈(a,b),0<x-a<δ,0<y-a<δ時有 f(x)-f(y)<ε.根據函數單側極限的Cauchy收斂原理,便知存在有限右極限f(a+0).同理,存在有限左極限f(b-0).

[1]華東師范大學數學系.數學分析[M].3 版.高等教育出版社,2003.
[2]呂通慶.一致連續與一致收斂[M].人民教育出版社,1981.

