一種二元高超聲速進氣道起動特性的尺度效應研究

凌 崗，李祝飛，肖豐收，姜宏亮，劉坤偉，高文智，楊基明

（1.中國科學技術(shù)大學近代力學系，合肥 230027；2.中國空氣動力研究與發(fā)展中心，四川綿陽 621000）

0 引 言

進氣道作為吸氣式高超聲速飛行器的主要部件，通過捕獲和壓縮空氣，為發(fā)動機燃燒室提供所需來流條件，其起動性能的好壞將直接影響推進系統(tǒng)能否正常工作。因此進氣道的起動性能是判斷高超聲速進氣道設計優(yōu)劣的一個關(guān)鍵指標［1］。

進氣道“起動”狀態(tài)，一般來說是指當進氣道內(nèi)部的流動現(xiàn)象沒有改變進氣道流量捕獲特性時，進氣道是起動的［2］。引起進氣道不起動的主要因素有：來流馬赫數(shù)過低，捕獲的流量難于全部通過喉道；激波邊界層等復雜干擾引起分離，造成流動壅塞；反壓過高，超出隔離段承受能力等等［3］。目前的研究對后兩者關(guān)注比較多。

在傳統(tǒng)的風洞實驗中，通常實驗模擬首先保證的是來流馬赫數(shù)相等，模型幾何相似，而在其他方面則可能會根據(jù)具體情況不得不適當放寬相似要求。例如受風洞尺寸的限制，實驗模型相對飛行器來說大多會有一定比例的縮小。在高超聲速進氣道相關(guān)研究中，為了充分體現(xiàn)內(nèi)外流耦合的特征，實驗模型往往需要采用機體與進氣道的一體化設計，這將進一步使得進氣道部分的尺寸受限而采用較大幅度的縮比模型。值得注意的是，對于不同尺度的進氣道模型，由于一體化耦合的復雜性，雷諾數(shù)、氣流熱力參數(shù)甚至壁溫等條件變化時，其流場結(jié)構(gòu)、邊界層轉(zhuǎn)捩位置、分離區(qū)大小等都會有一定程度的差別，從而影響進氣道的起動能力。由此可見，在高超聲速進氣道起動實驗中，尺度效應是不容忽視的問題。

尺度效應引起的差異，已引起國內(nèi)外學者的關(guān)注。在理論上，國內(nèi)外有不少研究指出了傳統(tǒng)風洞實驗模型設計縮尺比例由風洞尺寸決定的方法的不足，并提出了通過CFD對地面實驗結(jié)果進行修正，以得到與真實飛行條件下更為接近的數(shù)據(jù)［4－6］。Pulsonetti和Stalker在研究尺度對超燃沖壓發(fā)動機的影響時指出，不同尺度模型邊界層厚度的變化會對進氣道工作狀態(tài)產(chǎn)生一定的影響［7］。國防科學技術(shù)大學的金亮等研究了模型縮比尺度對飛行器整體性能的影響，指出內(nèi)流道摩阻系數(shù)不同會導致全尺寸模型與縮比模型阻力系數(shù)的不同［8］。南航的劉凱禮研究了不同尺度對進氣道動態(tài)迎角特性的影響，指出隨著進氣道尺度增加，放大后的進氣道動態(tài)迎角的影響也隨之增加［9］。在這些研究中，作者們大多關(guān)注的是進氣道縮尺效應對氣動特性的影響，而對于進氣道起動性能的研究尚未見到相關(guān)報道。

本文針對進氣道不同縮尺模型，開展自起動馬赫數(shù)的數(shù)值模擬，考察了這些縮尺模型之間起動性能的差異；同時對這種差異進行分析，期望找出其影響機理。在數(shù)值模擬的基礎(chǔ)上，選擇合適的模型進行必要的實驗考核和探討。

1 計算與實驗方法

為便于研究，減少過多復雜因素的干擾，選取了一種結(jié)構(gòu)簡單的二元進氣道模型。圖1（a）為采用的高超聲速二元混壓式進氣道模型示意圖。外壓段采用兩級壓縮，唇口為尖前緣設計，進氣道基準模型選用的內(nèi)收縮比為1.53，通過前后移動唇口位置可以改變進氣道內(nèi)收縮比。此構(gòu)型在本課題組前期研究中有一定的基礎(chǔ)，數(shù)據(jù)較為豐富，有利于結(jié)果的比較。基準進氣道構(gòu)型的具體尺寸參照相關(guān)文獻［10］。為提高計算效率，對三維計算域進行了半模等簡化，如圖1（b）所示。圖1（c）為實驗中所采用模型的照片。

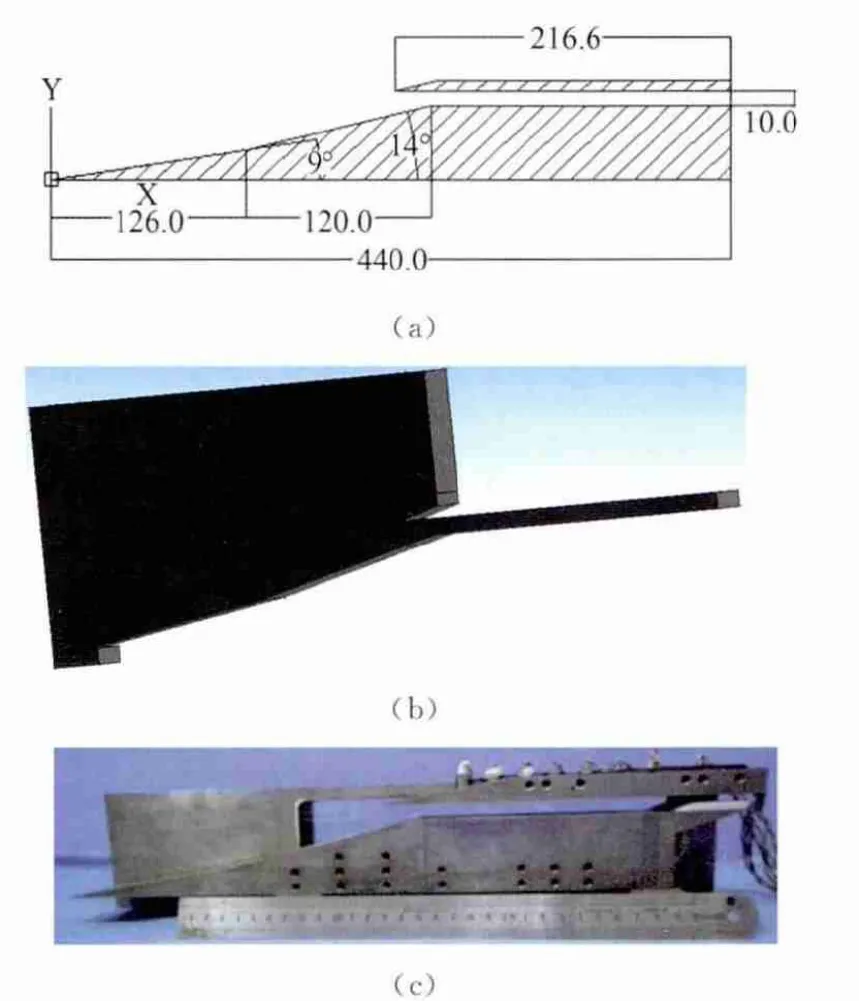
圖1 二元進氣道計算與實驗模型Fig.1 Diagram of 2Dhypersonic inlet and Computational domain

計算采用Fluent商用軟件進行N－S方程數(shù)值求解，湍流模型選擇S－A模型，通量格式采用AUSM格式。邊界條件采用壓力遠場條件、壓強出口條件和等溫無滑移固壁，粘性系數(shù)采用Sutherland公式計算。計算以低馬赫數(shù)（如M∞＝3）得到進氣道不起動流場，然后以上一步的收斂解作為初場，逐步增加來流馬赫數(shù)進行續(xù)算，直至進氣道起動，所對應的馬赫數(shù)即為自起動馬赫數(shù)［11］。為便于實驗驗證，本文采用激波風洞實驗中M∞＝5.9條件相同的動壓和總溫配置得到各來流馬赫數(shù)下的來流條件。在這種配置方法下，來流單位雷諾數(shù)Re1，∞約為5.1×106m－1。計算中涉及到變雷諾數(shù)的問題都是以此來流和構(gòu)型尺寸為基準條件（即表1中的1∶1尺度）進行的。

計算主要從兩個方面進行了考核，表1給出了數(shù)值模擬的主要內(nèi)容。算例1主要對不同縮比模型自起動馬赫數(shù)進行了模擬，以考核尺度效應對進氣道自起動馬赫數(shù)的影響。考慮到便于比較以及之后匹配雷諾數(shù)的方便，除基準模型外，計算中主要選擇了1∶2和1∶4模型進行數(shù)值模擬，另外，為增大考核范圍，還選擇了1∶10的模型進行對比。算例2主要考核雷諾數(shù)的影響，具體來說是通過提高1∶2模型的來流單位雷諾數(shù)使其和基準條件下1∶1模型的雷諾數(shù)相等來考核其起動能力。

表1 典型算例參數(shù)設置Table 1 Typical cases in the numerical simulation

計算中對1∶1模型分別給出了310萬和186萬左右兩種網(wǎng)格形式，近壁面處網(wǎng)格采用等比加密，壁面第一層網(wǎng)格高度5μm，計算得到兩種網(wǎng)格計算自起動馬赫數(shù)分別為4.6和4.7，變化很小。為減少計算量，采用網(wǎng)格較少的模型。另外，在來流M∞＝5.5時對比數(shù)值紋影與實驗結(jié)果，發(fā)現(xiàn)二者的流場結(jié)構(gòu)與實驗結(jié)果也吻合得較好（這在后文的實驗部分有所說明），表明計算結(jié)果具有較好的可信度。

2 結(jié)果討論與分析

2.1 不同縮尺模型的自起動馬赫數(shù)

在進氣道起動研究中，一般認為分離激波位于進氣道入口之后，沒有亞聲速溢流，即進氣道內(nèi)部的流動現(xiàn)象沒有改變進氣道流量捕獲特性時，認為進氣道處于起動狀態(tài)。圖2給出了1∶1模型不同馬赫數(shù)下的對稱面馬赫數(shù)分布和壁面極限流線圖。從圖中可以看出，在M∞＝3時，進氣道入口存在比較大的分離，分離激波在進氣道入口前，流道有明顯的壅塞，大量氣流從進氣道唇口外部溢出，進氣道處于不起動狀態(tài)。

在來流馬赫數(shù)增加到4.5和4.6時，分離激波位置雖然位于進氣道進口內(nèi)側(cè)，但由于流動的三維性，壁面極限流線圖上看到，實際上在側(cè)板和唇口交界處，仍有大量的氣流溢出，說明在這兩個來流馬赫數(shù)條件下，進氣道依然是不起動的。然而，當繼續(xù)增加來流馬赫數(shù)到4.7時，流場結(jié)構(gòu)卻出現(xiàn)了顯著的變化：對稱面馬赫數(shù)分布圖上看出入口處分離激波消失，進氣道內(nèi)部形成暢通的超聲速流道，壁面極限流線圖上也沒有明顯的溢流。表明在這個來流馬赫數(shù)下，進氣道已經(jīng)處于起動狀態(tài)。由此判斷，1∶1模型自起動馬赫數(shù)為4.7。同樣，對其他三種縮比模型自起動情況也進行了數(shù)值模擬。表2給出了各縮比模型自起動馬赫數(shù)比較情況。可以看出，隨著模型尺度的減小，進氣道自起動馬赫數(shù)有明顯的增加，特別是在模型縮小到1∶10時，進氣道很難實現(xiàn)自起動，自起動馬赫數(shù)已經(jīng)增加到了Mselfstart＝7.6。

圖2 1∶1模型不同來流馬赫數(shù)條件下流場Fig.2 The flow field in different Mach numbers of 1∶1model

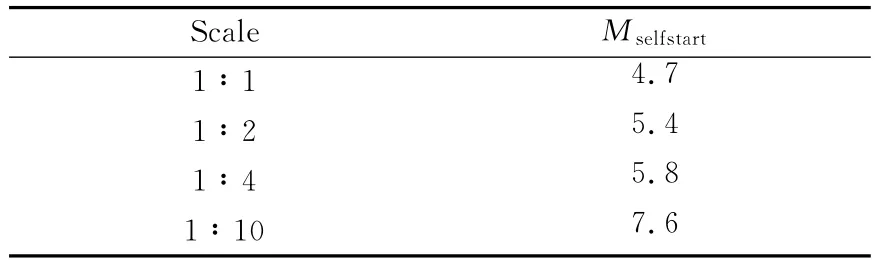
表2 各縮比模型對應的自起動馬赫數(shù)Table 2 Self－starting Mach number of different models

為分析導致不同縮尺模型自起動馬赫數(shù)不同的原因，對不同縮尺模型流場結(jié)構(gòu)進行了對比。為了突出尺寸的影響，這里固定單位雷諾數(shù)，并統(tǒng)一選擇M∞＝4.5的流場來比較各模型不起動狀態(tài)下的流場結(jié)構(gòu)。圖3分別給出了各縮比模型在M∞＝4.5時入口附近對稱面的馬赫數(shù)分布。從圖中可以直觀看到，隨著模型尺度的減小，進氣道入口處流動分離區(qū)隨之增大，分離激波逐漸被推向上游。

在相同單位雷諾數(shù)條件下，不同縮尺模型的雷諾數(shù)是不同的，而分離區(qū)的大小和雷諾數(shù)有很大的關(guān)系。因此有必要對雷諾數(shù)進行重點考察。

圖3 各模型M∞＝4.5對稱面馬赫數(shù)分布Fig.3 The Mach number contour in the symmetry plane of M∞＝4.5

2.2 雷諾數(shù)對進氣道起動性能的影響

為研究雷諾數(shù)的影響，對1∶2模型和1∶1模型雷諾數(shù)進行匹配。將1∶2模型單位雷諾數(shù)提高1倍，使其雷諾數(shù)和基準條件下1∶1模型雷諾數(shù)相等（主要通過改變來流密度來改變單位雷諾數(shù)）。圖4給出了提高單位雷諾數(shù)后1∶2模型在M∞＝4.5和M∞＝4.6條件下的流場。從圖中可以看出，M∞＝4.5時進氣道還處于不起動狀態(tài)，而在M∞＝4.6時，進氣道實現(xiàn)了起動，說明在此來流條件下，1∶2模型自起動馬赫數(shù)為4.6，遠低于原來（即雷諾數(shù)減半）的Mselfstart＝5.4，與1∶1模型的自起動馬赫數(shù)非常接近。

圖4 1∶2模型提高雷諾數(shù)后不同來流馬赫數(shù)條件下流場Fig.4 The flow field in different Mach number of 1∶2model after increasing Reynolds number

通過以上對比發(fā)現(xiàn)，在雷諾數(shù)提高以后，模型自起動馬赫數(shù)有所降低，即自起動能力有所增強。并且在相同雷諾數(shù)條件下，不同尺度模型的自起動馬赫數(shù)基本能保持一致。由此可以推斷，雷諾數(shù)確實是引起不同縮尺模型自起動性能不同的主要因素。

2.3 相關(guān)實驗結(jié)果討論

實驗在中國科學技術(shù)大學的激波風洞中進行，風洞可提供馬赫數(shù)5.5和5.9兩種典型的來流條件［12］，考核內(nèi)收縮比1.53和1.77的二元高超聲速進氣道模型的起動性能。M5.5來流總壓為0.78MPa，總溫為710K，單位雷諾數(shù)約為4.6×106m－1，而M5.9在基準單位雷諾數(shù)5.1×106m－1下的來流總壓為1.27MPa，總溫為810K。其中，內(nèi)收縮比1.77的進氣道模型由收縮比1.53模型唇口前移10mm得到（參見圖1（a））。采用在進氣道出口附近事先設置輕質(zhì)堵塊的方法，檢測進氣道的自起動能力［12］。

圖5為內(nèi)收縮比1.53進氣道模型在M∞＝5.5來流條件下自起動過程的紋影照片（t′對應于激波風洞實驗段流場開始建立的時刻）。輕質(zhì)堵塊的堵塞作用使得進氣道在風洞運行前期很快出現(xiàn)不起動，而當輕質(zhì)堵塊被吹出流道后，外壓縮面上的分離激波退回進氣道入口，并被喉道吞入，進氣道能夠重新建立穩(wěn)定的起動流場。表明內(nèi)收縮比1.53的進氣道在M∞＝5.5來流條件下，具有自起動能力。前文的數(shù)值模擬已經(jīng)指出，該進氣道的最小自起動馬赫數(shù)在4.7左右，實驗來流馬赫數(shù)高于其自起動馬赫數(shù)，進氣道能夠自起動。

圖6給出了內(nèi)收縮比1.53的1∶1模型在M∞＝5.5來流條件下的數(shù)值紋影，對比實驗結(jié)果可以看出，數(shù)值模擬的波系結(jié)構(gòu)與實驗結(jié)果吻合較好。

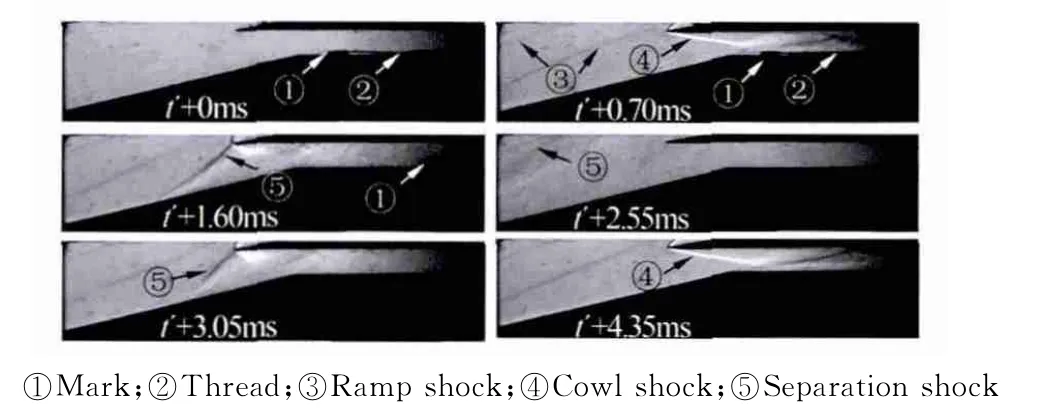
圖5 M∞＝5.5內(nèi)收縮比1.53進氣道自起動紋影Fig.5 Schlieren photographs of self－starting of the ICR＝1.53inlet at M∞＝5.5

圖6 M∞＝5.5內(nèi)收縮比1.53進氣道自起動數(shù)值紋影Fig.6 Numerical schlieren of self－starting of the ICR＝1.53inlet at M∞＝5.5

考慮到激波風洞所提供的來流馬赫數(shù)有限，為了進一步豐富實驗考核內(nèi)容，將模型的內(nèi)收縮比增大至1.77。

數(shù)值模擬表明（見圖7（a）），內(nèi)收縮比1.77進氣道的最小自起動馬赫數(shù)為5.8。圖7（b）給出了內(nèi)收縮比1.77進氣道模型在M∞＝5.5來流條件下，初始設置堵塊時的紋影照片序列。在堵塊被吹出流道后，進氣道入口始終被大范圍的流動分離區(qū)所占據(jù)，進氣道不能完成自起動過程。

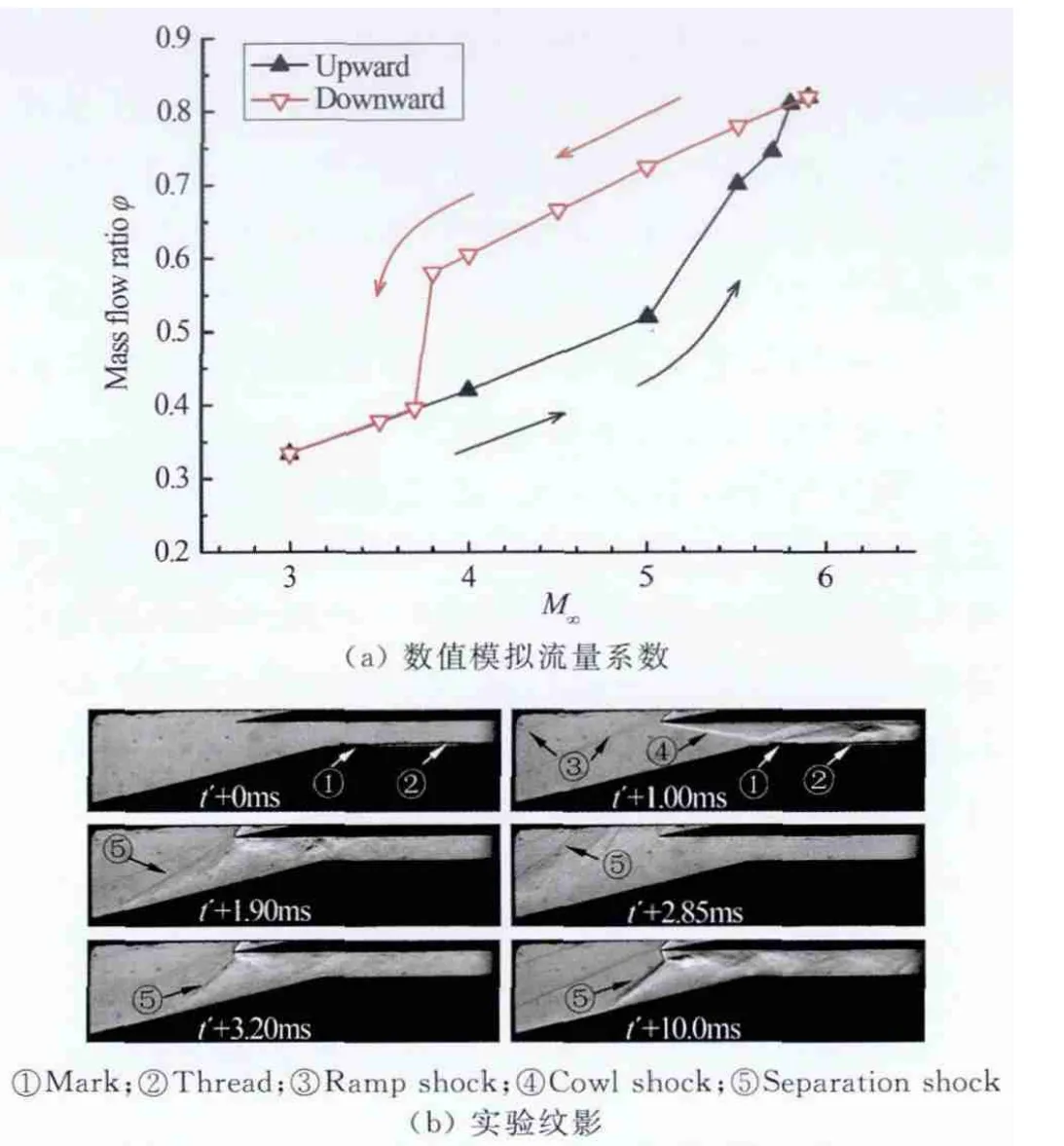
圖7 M∞＝5.5內(nèi)收縮比1.77進氣道不能自起動Fig.7 Self－unstarting of the ICR＝1.77inlet at M∞＝5.5

M∞＝5.9來流條件下，實驗結(jié)果如圖8所示，當流道恢復通暢后，進氣道能夠建立起動的流場結(jié)構(gòu)，表明內(nèi)收縮比1.77的進氣道在M∞＝5.9時，具有自起動能力。內(nèi)收縮比1.77進氣道在M∞＝5.5和M∞＝5.9兩種來流條件下的起動性能實驗結(jié)果與數(shù)值模擬的預報結(jié)果相符合，在一定程度上支持了數(shù)值模擬的合理性。

圖8 M∞＝5.9內(nèi)收縮比1.77進氣道自起動紋影Fig.8 Schlieren photograph of self－starting of the ICR＝1.77inlet at M∞＝5.9

另外，為研究雷諾數(shù)的影響，在M∞＝5.9來流條件下，對1.77內(nèi)收縮比模型在不同單位雷諾數(shù)下進行了試驗。圖9分別給出了單位雷諾數(shù)降低到原來的1／2和1／3的實驗紋影。在單位雷諾數(shù)降為1／2時，在堵塊被吹出流道后，進氣道入口始終有大范圍的流動分離區(qū)，進氣道不能實現(xiàn)自起動，然而有意思的是，當單位雷諾數(shù)繼續(xù)下降到1／3時，當堵塊被吹出，流道恢復暢通后，進氣道出人意料地建立了起動的流場結(jié)構(gòu)！這就意味著在更低的雷諾數(shù)下進氣道反而能夠起動。這與前文所得到的低雷諾數(shù)下不容易起動的結(jié)論完全相反。

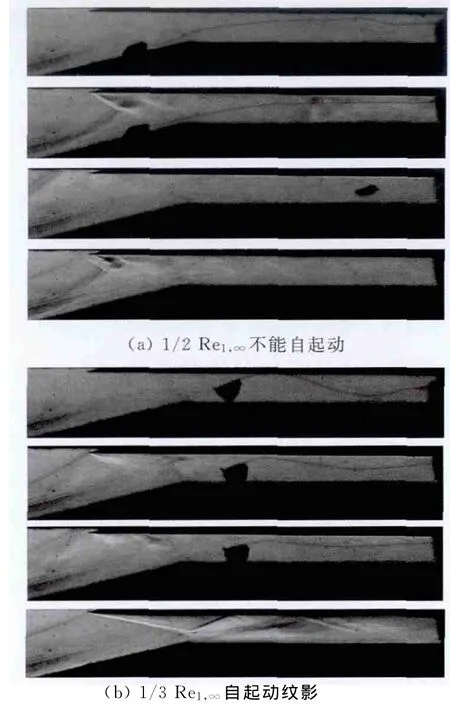
圖9 低雷諾數(shù)下實驗結(jié)果Fig.9 The experimental results under lower Reynolds number condition

3 來流流態(tài)對進氣道起動性能的影響

為了分析上述低雷諾數(shù)下進氣道異常起動的原因，這里對來流流態(tài)進行一定的數(shù)值模擬探討。考慮到模型尺度很小的低雷諾數(shù)流動時，流動很可能為層流狀態(tài)。已有的研究一般認為層流更容易引起流動分離，不利于進氣道的起動。但這一概念與本文的上述實驗結(jié)果已經(jīng)出現(xiàn)了難以自圓其說的矛盾。為弄清楚其中的原因，對進氣道不同來流流態(tài)下的自起動性能進行了數(shù)值模擬。為便于比較，數(shù)值模擬條件與實驗條件一致，進氣道內(nèi)收縮比為1.77，縮尺比例為1∶1。

圖10和11分別給出了湍流S－A模擬和層流模型在M∞＝5.9時的數(shù)值模擬結(jié)果。

從圖10中不難看出，在湍流狀態(tài)時，進氣道入口氣流呈壅塞狀態(tài)，壁面極限流線圖上也有明顯的溢流，顯然此時進氣道處于不起動狀態(tài)；而在層流狀態(tài)下，可以看到，盡管進氣道入口有較厚的邊界層存在，但其主體部分已經(jīng)形成暢通的超聲速通道，壁面極限流線圖上也沒有明顯的溢流，進氣道呈現(xiàn)出“起動”的特征。

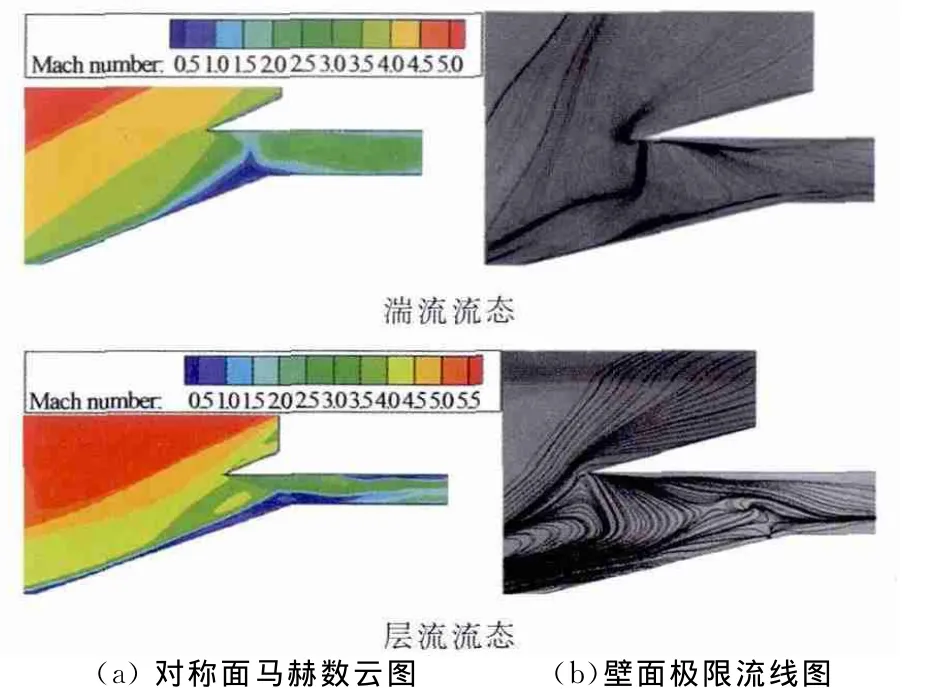
圖10 不同流態(tài)下數(shù)值流場Fig.10 The flow field of CFD in different flow model

為了更加清晰地和實驗結(jié)果進行對比，圖11給出了層流狀態(tài)下的數(shù)值紋影結(jié)果。對比圖9（b）的實驗結(jié)果可以發(fā)現(xiàn)，層流狀態(tài)下的數(shù)值紋影和實驗照片的波系結(jié)構(gòu)基本一致。特別是在圖9（b）的波系與下壁面的反射作用區(qū)域有一定的外移，表明該處存在相對較厚的局部低速流動區(qū)域；而圖11中對應的區(qū)域也存在著較為明顯的亞聲速低速流區(qū)，數(shù)值計算結(jié)果和實驗結(jié)果吻合較好。

圖11 層流狀態(tài)下數(shù)值紋影結(jié)果Fig.11 Numerical schlieren in laminar flow condition

這就是說，數(shù)值模擬結(jié)果可以得到低雷諾數(shù)下進氣道反而能“起動”的結(jié)果，而層流流態(tài)則在該“起動”過程中起著關(guān)鍵的作用。因此，通過實驗和數(shù)值模擬結(jié)果綜合考慮，作者對進氣道在低雷諾數(shù)下反而呈現(xiàn)起動狀態(tài)的傾向性解釋是，在低雷諾數(shù)下，來流偏向于層流流態(tài)，使進氣道呈現(xiàn)出一種“起動”狀態(tài)。當然，這種“起動”是否屬于真正意義上的起動，還有待于更深入的探討，探究其具體影響機理的工作也正在開展。

4 結(jié) 論

對進氣道在不同縮尺情況下的自起動性能進行了比較和分析，并開展了相關(guān)的實驗觀測，主要得到以下結(jié)論：

（1）在相同來流單位雷諾數(shù)下，不同縮尺模型在相同來流條件下自起動馬赫數(shù)會有差異，隨著模型尺度的減小，其自起動馬赫數(shù)升高；

（2）雷諾數(shù)是影響進氣道起動性能的重要因素，不同縮比模型在相同雷諾數(shù)下其自起動馬赫數(shù)基本保持一致；

（3）在模型縮比嚴重，雷諾數(shù)過于偏低時，實驗還觀察到進氣道的異常起動現(xiàn)象，對于其具體的形成機制還有待于進一步研究。

［1］ 范曉檣.高超聲速進氣道的設計、計算與實驗研究［D］.長沙：國防科學技術(shù)大學，2006.Fan Xiaoqiang.The design of the hypersonic inlet calculation and experimental research［D］.Changsha：National University of Defense Technology，2006.

［2］ Van Wie D M，Kwork F T，Walsh R F.Starting characteristics of supersonic inlets［C］.In 32nd ASME SAE，and ASEE，Joint Propulsion Conference and Exhibit.AIAA 1996－2914，1996.

［3］ David M Van.Wie.Scramjet inlet［M］.New York：AIAA，2000.

［4］ 陳謨.如何使用CFD來確定風洞實驗模型的縮尺比例［J］.宇航學報，2007，28（3）：594－597.Chen Mo.How to determine the scale ratio of wind tunnel test models by CFD［J］.Journal of Astronautics，2007，28（3）：594－597.

［5］ Weinberg S，Laganelli A，Martellucci A，et al.A plan for coupling wind tunnel testing with CFD techniques［C］.15thAerodynamics Testing Conference，1988，10.2514／6.1988－1996.

［6］ Boppe C.Future requirements of wind tunnels for CFD code verification［C］.14th Aerodynamic Testing Conference，1986，10.2514／6.1986－753.

［7］ Pulsonetti M V，Stalker R.A study of scramjet scaling［R］.AIAA 1996－4533.

［8］ 金亮，柳軍，羅世彬，等.數(shù)值模擬模型尺度與來流條件對實驗數(shù)據(jù)的影響［J］.空氣動力學學報，2010：00258－1825.Jin Liang，Liu Jun，Luo Shibin，et al.Numerical study on the influence of model scale and inflow conditions in wind tunnel experiment［J］.Acta Aerodynamica Sinica，2010：0258－1825.

［9］ 劉凱禮.高超聲速進氣道動／穩(wěn)態(tài)迎角特性研究［D］.南京：南京航空航天大學，2011.Liu Kaili.Research on aerodynamic characteristics of hypersonic inlets with dynamic／steady angle－of－attack［D］.Nanjin：Nanjing University of Aeronautics and Astronautics，2011.

［10］李祝飛，高文智，李鵬，等.二元高超聲速進氣道激波振蕩特性實驗［J］.推進技術(shù)，2012，33（05）：676－682.Li Zhufei，Gao Wenzhi，Li Peng，et al.Experimental investigation on the shock wave oscillation behaviors in a two－dimensional hypersonic inlet flow［J］.Journal of Propulsion Technology，2012，33（05）：676－682.

［11］游進，夏智勛，王登攀，等.高超聲速進氣道再起動特性及其影響因素數(shù)值模擬［J］.固體火箭技術(shù)，2011，34（02）：161－166.You Jin，Xia Zhixun，Wang Dengpan，et al.Numerical study on influencing factors of restarting characteristics for a hypersonic inlet［J］.Journal of Solid Rocket Technology，2011，34（02）：161－166.

［12］李祝飛，高文智，李鵬，等.一種進氣道自起動特性檢測方法［J］.實驗流體力學，2013，27（4）：14－18.Li Zhufei，Gao Wenzhi，Li Peng，et al.A test method for inlet self－starting ability detection［J］.Journal of Experiments in Fluid Mechanics，2013，27（4）：14－18.