基于T I N的土石方計算研究
徐 朱,方 強,翟 輝
(江蘇省地質調查研究院,江蘇南京 210018)
0 引言
近年來,隨著國民經濟不斷發展,各種工程項目越來越多,土石方計算越來越頻繁,而土石方量的計算對工程投資估算、工程量大小估算以及工程進度控制都能提供可靠依據。為了使工程技術人員脫離繁復的土方量手工計算,通過專家學者的不斷研究,率先在AutoCAD基礎上開發出了一系列成熟方法和程序,大大減輕了工程技術人員工作負擔,提高了計算速度。地理信息系統的出現,各種空間分析方法和手段的引入,使復雜的傳統空間分析任務變得更加簡單易行,特別是在ArcGIS中克立格插值[1,2]空間插值方法的幫助下,精確的TIN模型能快速模擬地面特征,使土方量計算的操作更加簡便、精度日益提高。
1 土方量計算的原理和方法
1.1 土方量計算的原理
土方量計算其實就是求取設計地面和自然地面之間物質的體積差。設計地面是按規則設計出來的,容易準確表達。而自然地面是由無數個點組成,人工采集的只能是有限的數據,表達自然地面特征也只能是無限的接近。假定自然地面是連續和漸變的,通過獲取有限的數據,也能模擬和近似表達真實的地面,微積分就是一種描述連續變化的方法[3,4],土石方的計算就是借鑒了微積分的思維方法,將地形分成若干微小單元,并將其地形特征簡化,以采集數據或空間插值數據近似表達各個單元的地形特征,分別計算各個微小單元的體積差,然后匯總求和,就得到了最后的土方量。這里也只是借用了微積分的思維方法,而不是具體運算程序,下一步是土石方計算的原理,如圖1所示。

圖1 土石方計算的原理
1.2 基于TIN的體積算法[5]
不規則三角網(TIN)是DEM的主要表現形式[6],是按照一定的規則將按地形特征采集的離散點連接成覆蓋整個區域的互不重疊的三角形,能很好地逼近原始地形表面,從而更好地表達真實的地面特征。基于TIN算法的土方量計算一般采用三棱柱法,利用場底和場頂之間的標高差建立三角網模型,然后利用泰森三角形的原理,把這個三角網模型分成若干個不規則的三棱柱,一個平面內,三點平均,從而計算三棱柱的體積,最后再將這若干個三棱柱加到一起,就是我們所求取的總的土石方量(填方量和挖方量)。
三棱柱法是沿地形等高線將每個方格的對角點連接起來劃分為兩個等腰直角三角形,根據各角點施工高度符號的不同,零線(即方格邊上施工高度為零、不填不挖的點的連線)可能將三角形劃分為兩種情況:三角形全部為挖方或全部為填方以及部分挖方和部分填方。
三棱柱法的計算公式是根據立體幾何體積計算公式推導出來的,比較精確。其計算方法如下:
下一步是全挖或全填的體積公式,如圖2所示:

上述公式(1)中,a是方格的邊長(m);h1、h2、h3是三角形各角點的施工高度(m)。
當劃分方格為部分挖方和部分填方時,零線將三角形劃分成底面為三角形的錐體和底面為四邊形的槭體,下一步是三棱柱法,如圖3所示。
錐體的體積為

槭體的體積為

上述公式(2)、(3)中,V錐是錐體的體積(挖方或填方)(m3);V槭是槭體的體積(挖方或填方)(m3);h1、h2、h3是三角形各角點的施工高度(均用絕對值代入),但h3常指錐體頂點的施工高度(m)。

圖2 三棱柱法(全填或全挖)

圖3 三棱柱法(部分填方和部分挖方)
2 實現步驟
在ArcGIS中,為了計算土方量,需要將設計地面和自然地面進行疊加,疊加后形成的交線就是回填區和開挖區的分界線。通過計算每一條分界線圍成的封閉區域的體積,就得到了每一個回填區和開挖區的體積,即為所求區域的填方量和挖方量。下一步是基于TIN的土方量計算流程,如圖4所示。
2.1 數據準備
土方量計算前首先準備高程點、等高線等數據,由于其格式一般是CAD的dwg格式,需要通過數據轉換,形成ArcGIS需要的Shapefile格式。
2.2 數據檢查
查看高程點、等高線的屬性數據中是否有高程字段并且高程字段非空。
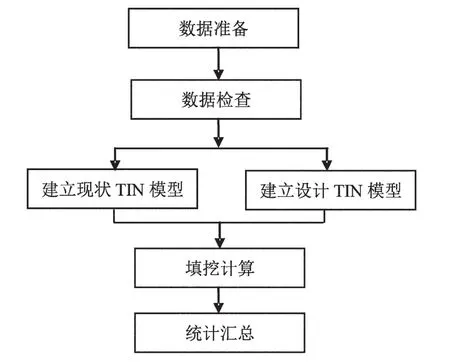
圖4 基于TIN的土方量計算流程圖
2.3 生成TIN模型
在ArcGIS中,使用3D Analyst模塊,選擇高程點和等高線數據通過克立格空間插值[7]進行TIN模型構建。需要注意的是,要先選擇好存放高程值的字段。根據設計前后地形,分別生成 TIN1和TIN2。
2.4 填挖計算
利用Cut/Fill工具對TIN文件進行填挖計算,最后會生成一個圖層,圖層上分色顯示回填區和開挖區的范圍。
2.5 統計匯總
生成的圖層屬性表中,正值表示要填充的土方量,負值表示要挖掉的土方量,通過統計,即可分別計算出填方量和挖方量。
3 工程實例分析
筆者參與了連云港市某廢棄礦山土地整治土石方計算工作,該地區地表凹凸不平,最低處高程66m,最高處高程100m,根據整治設計目標,采用了ArcGIS進行土方量計算。
3.1 數據獲取
收集該整治區的高程點、等高線數據,特別在地面起伏處,利用全站儀補測高程點數據,增加采集點密度,并將實測點輸入計算機。
3.2 TIN模型建立
利用ArcGIS系統的3D分析模塊根據現狀圖和設計圖中高程點、等高線數據按照10m×10m柵格單元進行插值,下一步是最后分別生成現狀TIN和設計TIN,如圖5和圖6所示。
3.3 計算工程填挖方
根據生成的設計前、后TIN表面,利用3D分析模塊下的Cut/Fill工具生成一個新的圖層,下一步計算產生的填挖方柵格圖,如圖7所示,該圖層的右下角圖例中,Net Gain表示凈填方,Net Loss表示凈挖方,Unchanged表示不填不挖。

圖5 現狀TIN(按高程分類顯示)

圖6 設計TIN(按高程分類顯示)

圖7 計算產生的填挖方柵格圖

表1 工程填挖方統計表
下一步是打開該柵格要素屬性表,如表1所示,其中表內字段Volume值大于零的表示凈填方,小于零的表示凈挖方,等于零的不填不挖,通過鼠標右鍵點擊Volume字段,可以統計柵格體積,總計為72 269,填方大于挖方。
4 結論與建議
基于TIN的土石方計算,是通過設計前后地形模型疊加找出回填區和開挖區的分界線,再對每一個封閉區域通過求取體積差來統計每一個回填區和開挖區的土方量,最后統計匯總得出總土方量的一種方法。相比其他傳統土方量計算方法,其計算簡單、快速,自動化程度高,適用于各種地形,特別是復雜地形。
因此,在應用TIN模型計算土方過程中有如下建議:①前期對數據進行檢查,高程字段非空,否則將產生錯誤;②生成的現狀TIN和設計TIN范圍應保持一致;③優先選擇閉合等高線參與TIN模型建立。
該方法對基礎數據要求較高,計算精度跟地形、坡度及柵格大小等因素有關,一般情況下,柵格越小,精度越高。這種方法簡單、可靠,適用范圍較廣,可推廣性較強。
[1]俞志新,李艷,黃明祥.地統計克立格插值法在工程土方計算中的應用[J].浙江水利科技,2003(4):37-38,47.
[2]陳勇.利用ArcGIS地統計分析進行土地平整土方量計算的研究[J].安徽農業科學,2007(1):70-71,103.
[3]程不時.突變論及其應用[J].科學通報,1978(9):513-522.
[4]欣欣.突變論模型[J].哲學動態,1990(2):20-21.
[5]周啟鳴,劉學軍.數字地形分析[M].北京:科學出版社,2006.
[6]THOMPAONJA,BELLJC,BUTLERCA.Digital Elevation Model Resolution:effect on terrainattribute calculation and quantitative sail landscape modeling[J].Geoderma 2001(1).
[7]湯國安,楊昕.ArcGIS地理信息系統空間分析試驗教程[M].北京:科學出版社,2006.

