基于密度核估計的貝葉斯網絡結構學習算法

韓紹金 ，李建勛

HAN Shaojin1，2，3,LI Jianxun1，3

1.上海交通大學 電子信息與電氣工程學院，上海 200240

2.中國人民解放軍63926部隊

3.教育部系統控制與信息處理重點實驗室，上海 200240

1.School of Electronic Information and Electrical Engineering,Shanghai Jiaotong University,Shanghai 200240,China

2.Unit 63926 of PLA,China

3.Key Laboratory of System Control and Information Processing,Ministry of Education,Shanghai 200240,China

1 引言

貝葉斯網絡（Bayesian Networks，BN）是融合了概率分布表的有向無環圖，它將樣本信息與先驗知識相結合，具有形象直觀的數據表達特點，以結構依賴和概率表示的形式分別描述了變量之間定性與定量依賴關系，理論基礎堅實，表述方式直觀，推理能力強大，是不確定性問題建模和推理的有效工具。

準確高效地學習貝葉斯網絡結構和參數，是有效利用貝葉斯網絡解決實際問題的基礎，是貝葉斯網絡理論研究的熱點，其內容包括確定貝葉斯網絡的結構（有向無環圖）和學習節點變量的條件概率分布，即為結構學習和參數學習。其中結構學習是貝葉斯網絡學習的重點和基礎，目前在結構學習的領域已經研究發展了許多經典實用的算法，如爬山法[1]，MMHC法[2]等，這些方法有扎實的理論支持，并且在各工程領域都得到了廣泛的應用，但這些方法的實現和應用都是基于大規模數據集（完備或者經補充后完備），而在實際工程應用中，受限于環境、材料、時間等因素，很多實驗往往不能夠多次重復，使得能夠獲得的實驗數據較少，樣本規模很小，這樣的小樣本數據集里能夠表達的信息不夠完整，許多數據的統計因子缺失，由此進行的貝葉斯網絡結構學習的準確性和可靠性無法保證。由此衍生出基于小樣本數據集的貝葉斯網絡結構學習問題的研究。目前研究比較多的集中在兩個方面，一種是研究基于小樣本數據集直接進行學習得到主體結構，然后利用數據修正等性質進行優化[3]，另一種是通過拓展數據集來增加樣本規模[4]，以此提高結構學習的可靠性。基于數據集的Bootstrap抽樣是常用的數據拓展方法，但傳統的Bootstrap抽樣是對數據集的可重復抽樣，沒有增加額外信息，學習效果無法得到實質性的改進。

在本文提出的算法中，將概率密度核估計的方法引入小數據集的拓展過程，將所得到的拓展數據集用于貝葉斯網絡的深入學習，還通過計算互信息度確認了節點次序，較好地改善了Bootstrap抽樣方法無法得到額外有效信息的缺點，彌補了K2算法需要確認節點先驗次序的不足，有效地提高了貝葉斯網絡結構的學習效果。

2 K2算法介紹

現有的貝葉斯網絡結構學習方法分成兩類，一類是基于評分搜索的學習方法，另一類是基于約束滿足的學習方法[5]。其中評分搜索的方法過程簡單規范，更被人們采用。Cooper提出的K2算法是簡單經典的方法之一。K2算法的基本思想是定義評價網絡結構模型優劣的評分測度函數，首先給定一個包含所有節點的變量順序δ和最大父親節點個數π。在搜索過程中，按給定順序逐個考察δ中變量，確定其父親節點，添加相應邊。對變量 Xj，假設已經找到的父親節點為πj。如果 Xj的父親節點個數還未達到最大值π，即|πj|＜π，則應繼續考察δ中排在 Xj之前而還不是 Xj父親節點的變量，在其中繼續尋找父節點，操作步驟為：從這些變量中選出使得新網絡評分Vnew達到最大的 Xi，然后將Vnew與舊網絡評分Vold比較：如果Vnew＞Vold，則 Xi為 Xj的父節點；當父親節點數到達最大值或者網絡評分無法提高時停止為Xj尋找父親節點。其評測函數定義為：

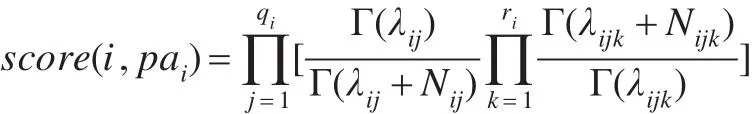
學習流程偽代碼為：

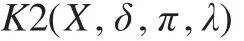
輸入：X={X1，X2，…，Xn}為一組變量，δ為一個變量順序，π為變量最大父親節點個數，λ為完整的數據集。

輸出：經過結構學習得到的貝葉斯網絡。

ζ=由按照次序排列的全部節點組成的無邊圖

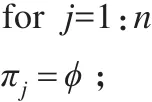
3 基于概率密度核估計的貝葉斯網絡結構學習算法

傳統的基于小樣本數據集的貝葉斯網絡結構學習問題通常采用Bootstrap[6-8]抽樣方法來完成小樣本的拓展，然后基于拓展后的數據集采用大規模數據集的結構學習算法完成學習。但由于Bootstrap抽樣方法產生的樣本只是來源于原樣本，因此極有可能得到的拓展樣本與原樣本極為相似，且不會改善小樣本集里的信息缺失的情況，特別在樣本容量極小的情況下，這樣的特性會使得概率分布集中于少量點，體現在學習得到的貝葉斯網絡里便是這些點對應的連接邊出現的概率較高，而原始小樣本缺失的數據信息所對應的連接邊無法得到補充。為改善Bootstrap抽樣方法不能補充缺失數據的問題，本文以概率密度核估計的方法對原始小樣本進行拓展得到大數據集，然后基于大數據集運用K2算法進行結構學習，由于概率密度核估計方法是估計概率密度分布后再進行重采樣，因此可以有效補充小數據集缺失信息，以此進行結構學習得到的模型更加全面準確。

3.1 概率密度核估計

密度核估計（kernel density estimation）是估計未知概率密度函數的方法，是非參數檢驗方法之一，由Rosenblatt[9]和Emanuel Parzen[10]提出。密度核估計方法不利用有關數據分布的先驗知識，對樣本的總體分布不作任何假設，是一種從樣本自身出發研究數據分布特征的方法，在統計學理論和應用領域均受到高度的重視。

設 X1，X2，…，Xn是從一維總體 X中抽出的獨立同分布樣本，X具有未知密度函數 f(x)，x∈R，則 f(x)的核估計為：

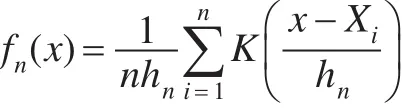
其中 K(·)為 R=(-∞，+∞)上的Borel可測函數，稱為核函數，在有意義的核估計里，核函數應當是概率密度函數，hn是個同n有關的正數，稱為窗寬或帶寬[11]。在獨立同分布的情況下，核估計量具有逐點漸進無偏性和一致漸進無偏性、均方相合性、強相合性、一致強相合性等，這使得核估計在非參數密度估計中占有重要地位。

3.2 概率密度核估計參數優化

概率密度核估計的效果，既與樣本規模n有關，也與核函數K(·)和窗寬h的選擇有關，在給定樣本的情況下，決定概率密度核估計性能好壞的變量就只有核函數K(·)和窗寬n。核函數的選擇不是密度估計中最關鍵的因素，因為選用任何核函數都能保證密度估計具有穩定相合性。因此在實際工程應用中，只需選擇滿足一定條件的核函數即可。核函數的確定一般需要滿足下列條件：（1）函數對稱且 ∫K(t)dt=1；（2）一階矩等于零，方差為有限值；（3）函數連續。常見的核函數有Epanechikov核、Parzen核、Triweight核等。見表1。

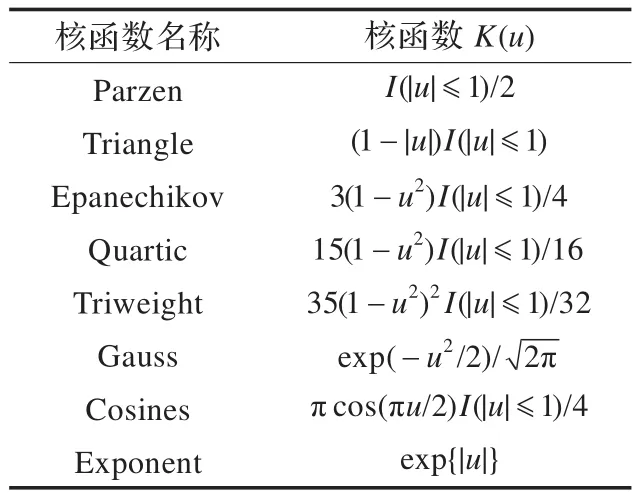
表1 常見核函數

常用來度量核估計性能的一種測度是積分均方誤差MISE，表達式為：

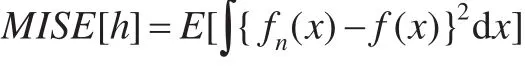
對其進行展開計算，并略去高階小量得到：

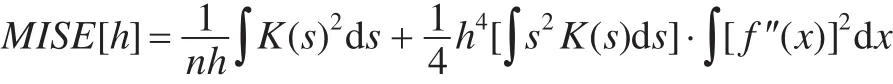
在上式中，第一項是估計的方差，第二項是偏差項。由此可知，當核函數固定時，若窗寬選得過大，偏差會隨之變大，但方差能夠得到抑制，此時x經過壓縮變換之后 fn(x)對 f(x)有較大的平滑作用，淹沒了密度的細節部分；若窗寬選得過小，偏差得到改善，但方差隨之增加，這是因為此時引起了隨機性影響的增加，fn(x)有較大的波動，f(x)的某些重要特性可能被掩蓋。因此窗寬的選擇需要同時考慮偏差和方差的影響。

3.3 基于貝葉斯網絡概率密度核估計的小樣本數據集拓展

貝葉斯網絡得到的數據集為多維數據，數據維度取決于網絡節點，且各維度之間存在相互關聯和耦合，因此在貝葉斯網絡的小樣本數據拓展中，必須將數據集作為多維自耦合的整體來考察。

設將要學習的貝葉斯網絡節點數為M，則可知得到的數據 X為 M 維變量，設 X1，X2，…，Xn為要得到的 X的樣本，則由上文可知數據集X的概率密度函數 f(X)的核估計為：

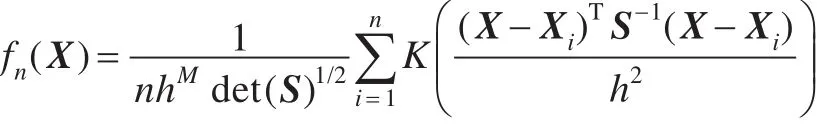
其中：X=(x1，x2，…，xM)T，Xi=(xi1，xi2，…，xiM)T(i=1，2，…，n)；h為窗寬，n為樣本容量；S是 M×M 維對稱樣本協方差矩陣[12]。

依潘涅契科夫[13]經過統計研究得出，當概率密度核估計的窗寬系數確定時，核函數的不同對MISE的影響很小。本文以標準高斯函數作為核函數。標準高斯函數密度函數為：

在核函數固定的情況下，窗寬隨數據規模的增大而減小。窗寬的確定應考慮數據集的密集程度變化，在數據集密集的部分，將窗寬選小一點，這樣可以有效保留數據細節，保證數據集的精確可靠；在數據集稀疏的部分，將窗寬取大一些，這樣可以剔除數據集毛刺，減小數據拓展開銷。最優窗寬的具體計算方法很多。這里使用LSCV法。LSCV是基于積分平方誤差（Integrated Square Error，ISE）最小準則的一種計算方法。對多維隨機變量X ，ISE為：

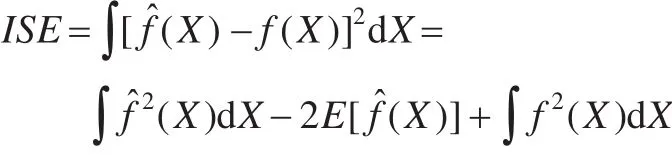
式中最后一項與窗寬無關。LSCV就是取式中前兩項進行最小化，即

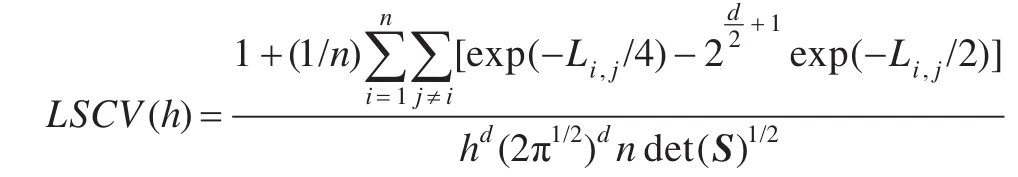
多維數據樣本集最簡單的形式是二維數據樣本，本文以此為例，驗證多維數據核估計效果，取均值矩陣M=，協方差矩陣，樣本采樣率（樣本集規模）N=300，得到仿真結果如圖1所示。

由圖可知，以二維數據樣本為例的多維數據核估計取得了良好效果，所得概率密度函數十分貼近給定函數。

3.4 基于互信息度的變量順序確定

傳統的K2算法需要指定一個包含所有節點的變量順序，而這個變量順序在實際問題中通常是無法先驗預知的。需要通過對樣本數據的學習來識別最佳變量順序，將其作為K2算法的輸入變量之一，然后再利用K2算法對樣本數據進行學習得到貝葉斯網絡。本文提出一種基于互信息度確認變量順序的方法。

圖1 維數據樣本集核估計效果

兩個變量之間的關聯程度可用互信息度表示，記為I[X;Y]，定義如下[14]：

其中H[X]表示隨機變量X的信息熵，H[X|Y]表示給定Y條件下變量X的信息熵，定義如下：

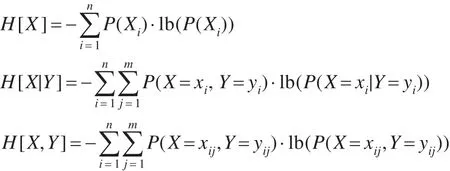
其中，n和m分別表示隨機變量X和Y的取值狀態個數，根據互信息的定義，互信息度具有對稱性，即I[X;Y]=I[Y;X]。

互信息度取值越大，表明兩個變量間的聯系越緊密，則兩個節點間有邊連接的可能性越大。基于這樣的性質，可以構建一條節點鏈，具體步驟為：

（1）計算得到兩兩節點的互信息度Ii[Xi;Yi]。

（2）對互信息度Ii[Xi;Yi]進行降序排列。

（3）依據排列順序，依次取出一對節點，判斷兩節點之間是否有邊連接或者連接后是否形成回路，如果都沒有，則在兩個節點之間增加一條邊。

（4）當所有節點都取完后，則形成一條節點鏈。

得到的節點鏈是一個無向節點鏈，作為K2算法的節點順序輸入，還需要確認節點鏈的方向，在樣本集中提取小規模樣本分別按照正向節點順序δ1和反向節點順序δ2的順序利用K2算法進行結構學習，最終學習分別得到分數Score1和Score2，如果Score1＞Score2，則取δ1作為變量順序輸入K2算法進行結構學習，反之取δ2作為結構變量高的順序。

3.5 基于概率密度核估計的數據集拓展和K2結構學習

由上文可知，概率密度核估計的方法在進行多維數據樣本的密度函數估計時取得了良好效果，在此基礎上利用重抽樣得到拓展數據集能有效克服Bootstrap抽樣方法樣本單一、數據集不確實的問題。

K2算法是網絡結構學習中有效的打分搜索方法，但該算法要求具備大規模樣本集以確保可以獲得正確的網絡結構，以及需要已知輸入網絡節點的邏輯次序。由于在實際應用中，多數情況下難以獲得大規模樣本集，也不是每個網絡都能夠得到先驗的節點順序，因此K2算法在工程實際的應用受到限制。本文將概率密度核估計、互信息度學習以及K2算法結合，提出基于小規模數據集學習的KI-K2貝葉斯網絡結構學習算法，算法流程如圖2所示。

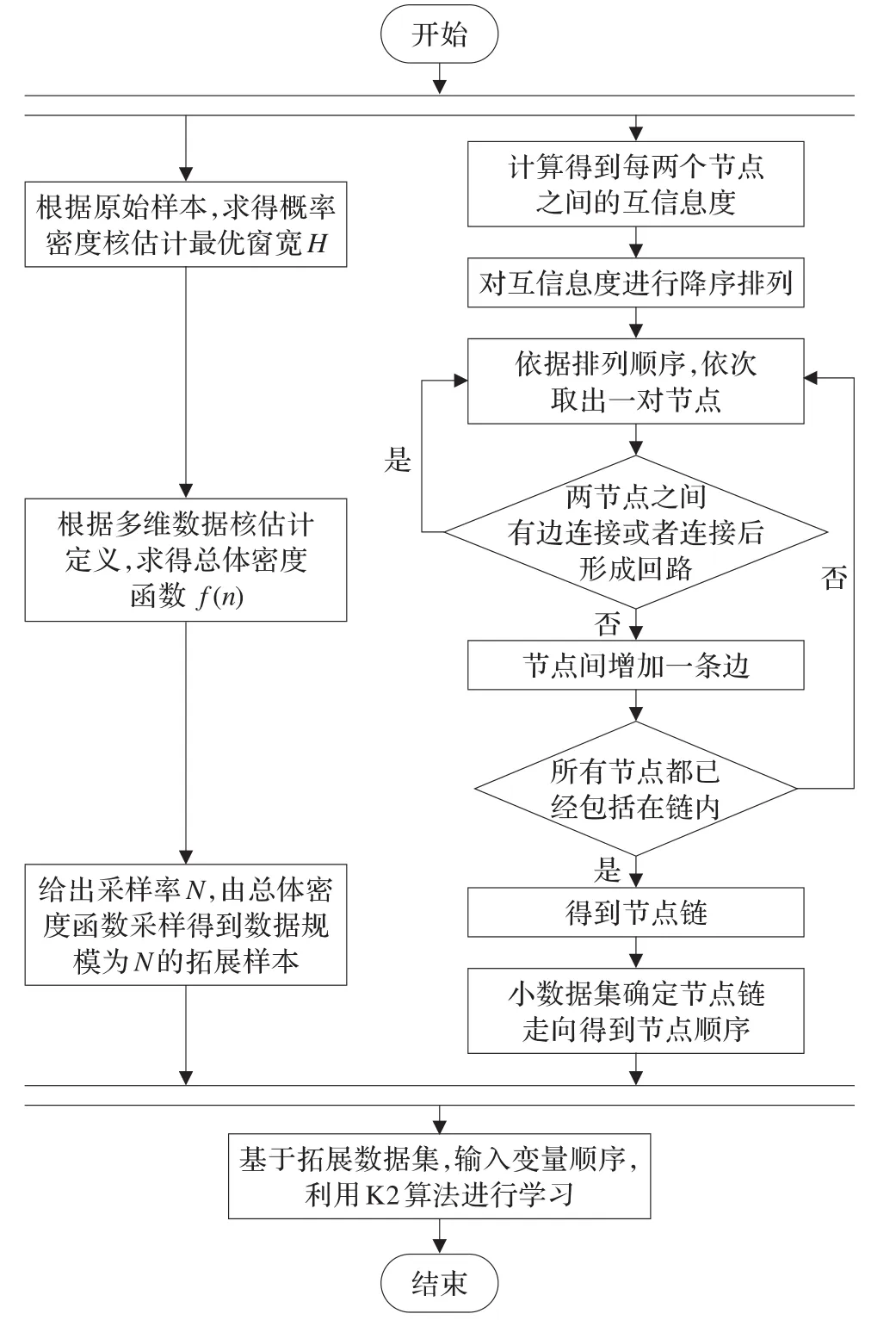
圖2 KI-K2算法流程圖

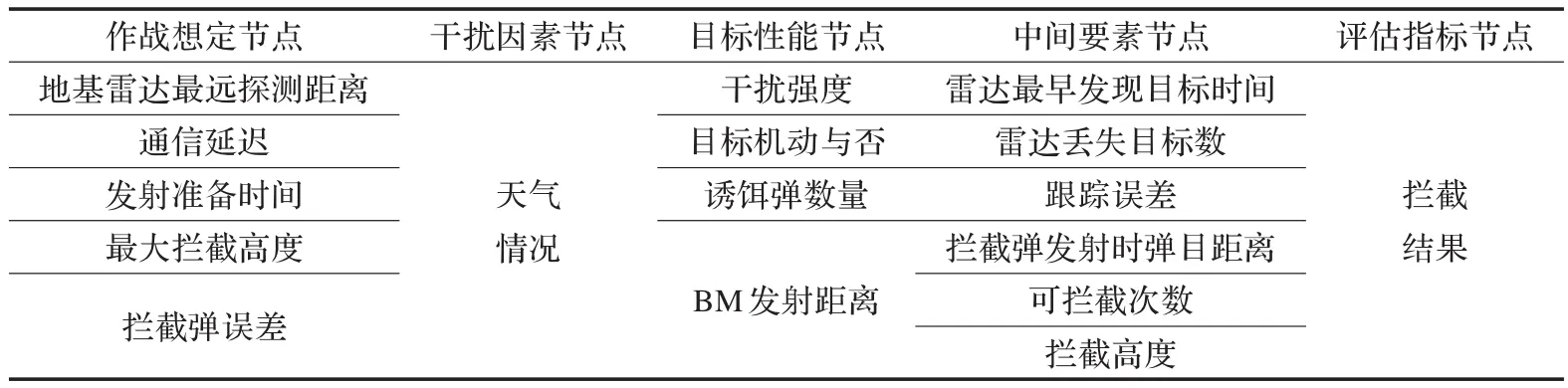
表2 數據設計表

KI-K2算法以概率密度核估計來進行原始數據集拓展，同時利用互信息度進行節點次序確認，然后與K2算法學習網絡結構相結合進行網絡學習，這種算法能夠充分發揮概率密度核估計在數據集拓展上的優勢，為后期網絡結構學習提供相對全面準確的樣本數據，同時將互信息度確認節點次序與K2算法相結合，能夠最大限度地保留獨立性測試高效與K2算法快速準確的特點，使得K2算法擺脫節點次序這一先驗輸入的限制，在實際工程問題中更具有實用性。

4 仿真驗證

以貝葉斯網絡為工具，來評估導彈攔截系統的效能，以此為實例來進行學習驗證本文提出的KI-K2算法的性能。

彈道導彈防御系統一般由搜索探測系統、指揮控制系統、跟蹤制導系統、攔截彈系統、評估系統組成[15]。評判其效能有以下指標：

（1）作戰能力。主要包括：預警探測能力、跟蹤能力、通信能力、攔截能力等。

（2）生存能力。

（3）可靠性。

假定攔截系統為PAC-3（“愛國者”-3）末段低層攔截系統，進攻彈為“潘興”-2中程戰術彈道導彈。仿真實例為PAC-3多次攔截1枚彈道導彈。可靠實驗數據表明，其貝葉斯網絡節點可設計如表2。

導彈攔截系統全因素貝葉斯模型如圖3所示。

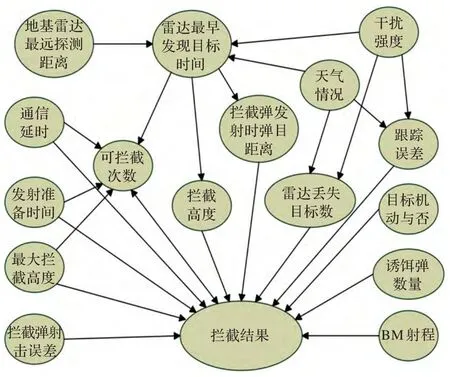
圖3 導彈攔截系統全因素貝葉斯模型

實驗過程中共選取實驗設計中的7個因素（見表3），并對每個因素取值進行離散化得到2個狀態。

表3 最終數據設計表

得到貝葉斯網絡如圖4所示。

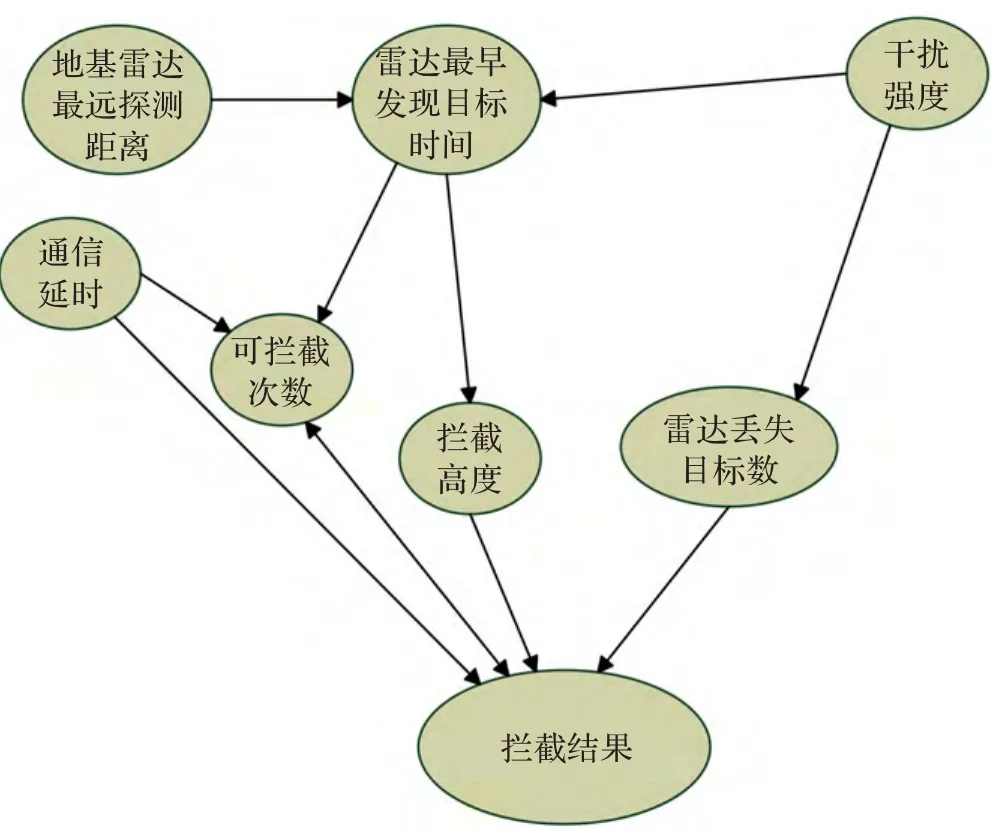
圖4 生成貝葉斯網絡

將均勻分布生成的隨機數與節點的條件概率對比便可實現對節點的采樣，基于給定的貝葉斯網絡結構，按照網絡結構順序依次對節點進行采樣便可生成對此網絡的一組隨機采樣數據。利用Matlab貝葉斯網絡工具箱里面的sample_bnet函數可產生規模為N的小數據集，然后基于數據集使用Bootstrap方法以及概率密度核估計的方法分別進行數據拓展，然后利用K2算法進行結構學習，最后進行比較。

本文采取的各個參數如下：Bootstrap抽樣為原數據規模10倍，密度核估計選取核函數為高斯函數。為減少偶然誤差，實驗重復進行10次，取平均值作為實驗結果輸出。

實驗環境為：硬件為Intel?CoreTMi5-2310 2.90 GHz 2.89 GHz；操作系統為Windows XP；編程軟件為matlabR2010a。

用IE代表學習結構比原網絡結構多的邊，ME代表學習結構比原網絡結構缺的邊，RE代表學習結構與原網絡結構相比反轉的邊，分別取原始樣本數N=1 000，500和100，得到仿真結果如表4～6所示。

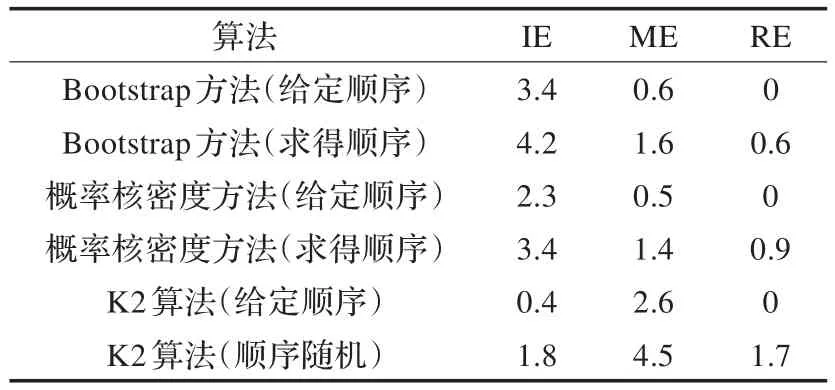
表4 原始樣本數N=1 000時各算法仿真效果

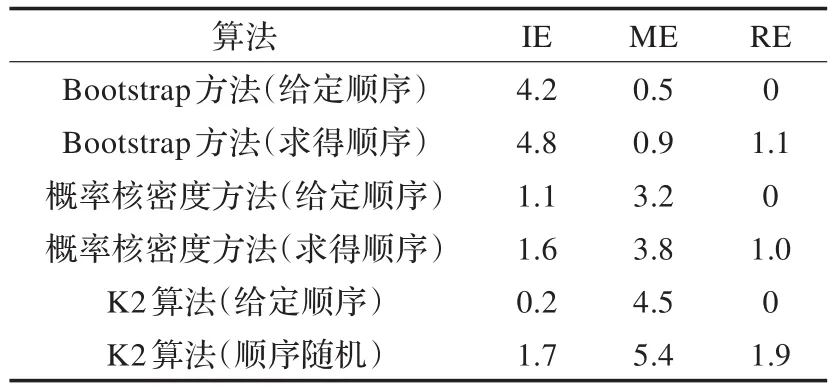
表5 原始樣本數N=500時各算法仿真效果

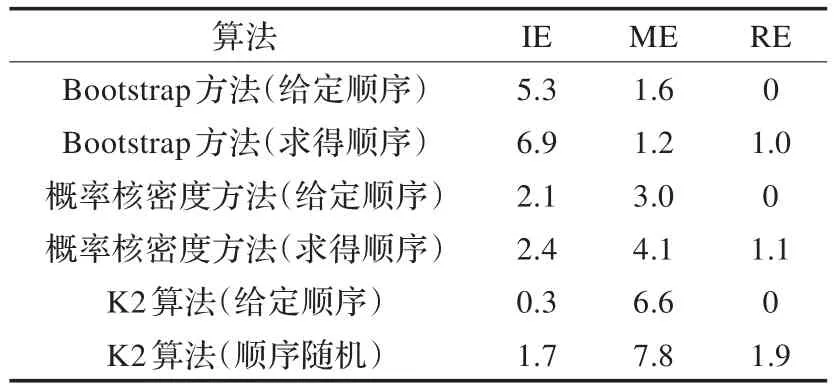
表6 原始樣本數N=100時各算法仿真效果

由實驗結果可知：

（1）小樣本數據集條件下，概率密度核估計拓展數據集后進行貝葉斯網絡結構學習效果比Bootstrap抽樣方法拓展數據后進行結構學習的效果好，隨著數據集減小，學習誤差增大，但該算法效果優越性越明顯。

（2）小樣本數據集條件下，給定先驗節點順序的概率密度核估計拓展數據集后進行貝葉斯網絡結構學習效果同樣優于給定先驗節點順序的K2算法，隨著數據集減小，學習誤差增大，但該算法效果優越性越明顯。

（3）小樣本數據集條件下，基于互信息度求得先驗節點順序的概率密度核估計拓展數據集后進行貝葉斯網絡結構學習效果與給定先驗節點順序的K2算法基本持平，優于隨機順序的K2學習算法，證明該算法確實有效，改善了必須指定節點順序的不足。

（4）采用指定節點順序的K2算法進行結構學習的話反向的邊一直等于0是因為K2算法得到了順序的變量邏輯結構，因此不會產生反向的邊。

5 結束語

本文提出了利用概率密度核估計方法對樣本數據集進行拓展，利用互信息度推算節點邏輯順序，然后基于拓展后的樣本數據集將確認的節點順序進行貝葉斯網絡結構學習的算法，最后通過仿真驗證可以看到，本文提出的算法具有較強的結構學習能力和良好的學習速度，在實際工程背景下是一種可靠高效的結構學習方法。

[1]Cooper G F，Herskovits E.A Bayesian method for the induction of probabilistic networks from data[J].Machine Learning，1992，9（4）：309-347.

[2]何德琳，程勇，趙瑞蓮.基于MMHC算法的貝葉斯網絡結構學習算法研究[J].北京工商大學學報：自然科學版，2008，26（3）：43-48.

[3]王雙成，冷翠平，李小琳.小數據集的貝葉斯網絡結構學習[J].自動化學報，2009，35（8）：1063-1070.

[4]Borchani H，Amor N B，Khalfallah F.Learning and evaluating Bayesian network equivalence classes from incomplete data[J].International Journal of Pattern Recognition and Artificial Intelligence，2008，22（2）：253-278.

[5]金焱，胡云安，張瑾，等.K2與模擬退火相結合的貝葉斯網絡結構學習[J].東南大學學報：自然科學版，2012，42（S1）：82-86.

[6]Efron B.Bootstrap methods：another look at the jackknife[J].The Annals of Statistics，1979，7（1）：1-26.

[7]陳峰，楊珉.Bootstrap估計及其應用[J].中國衛生統計，1997，14（5）：5-7.

[8]劉偉，龍瓊，陳芳，等.Bootstrap方法的幾點思考[J].飛行器測控學報，2007，26（5）：78-81.

[9]Rosenblatt M.Remarks on some nonparametric estimates of a density function[J].The Annals of Mathematical Statistics，1956，27（3）：832-837.

[10]Parzen E.On estimation of a probability density function and mode[J].The Annals of Mathematical Statistics，1962，33（3）：1065-1076.

[11]郭照莊，霍東升，孫月芳.密度核估計中窗寬選擇的一種新方法[J].佳木斯大學學報：自然科學版，2008，26（3）：401-403.

[12]李德旺，陳興，喻達磊，等.多維密度核估計的Bootstrap逼近[J].西南大學學報：自然科學版，2007，29（11）：34-37.

[13]Epanechnikov V A.Nonparametric estimation of a multidimensional probability density[J].Theory of Probability Application，1969，14（1）：153-158.

[14]Herskovits E.Computer-based probabilistic-network construction[D].Stanford：Stanford University，1991.

[15]禹磊，唐碩.基于貝葉斯網絡模型的導彈防御效能評估研究[J].飛行器測控學報，2012，31（5）：89-94.