灰色殘差模型在城市工業需水量預測中的運用
王鵬,黃顯峰,崔延松
(1.河海大學 水利水電學院,江蘇 南京 210098;2.南通大 學交通學院,江蘇 南通 226019)
0 引言
水是生命之源,也是工業生產活動中不可缺的重要資源,故工業需水量預測是直接影響到一個城市工業持續穩定發展的重要工作內容[1]。現有很多常用的需水量預測方法,如ARMA 方法、回歸分析法、指標分析法、灰色預測法、人工神經網絡法、系統動力學方法等[2]。但很多方法和模型需要大量的歷史數據資料,且對數據的要求很高,考慮的影響因子很多,各因子之間關聯復雜,限制了很多方法的使用,但其中不乏簡單易行的方法,例如灰色模型。
灰色模型具有建模原理簡單,計算方便,所需樣本少,預測精度高,不考慮影響因素和因子等特點[3-5],已成功應用到多個行業和社會領域的需求預測中。然而實踐過程中得到的預測結果卻不盡如人意,其原因是現實中的統計數據經常呈現出毫無規律,很難滿足指數規律,這樣的數據帶入傳統灰色模型無法滿足預測精度,也無法保證預測值的可信度;再者灰色模型不適合對客觀事物做長期預測,會出現系統誤差。故人們越來越渴求對灰色模型進行修正和改進,來更精確地對客觀事物進行長期預測。灰色殘差模型正是在這樣的背景下出現的一種改進的灰色模型,通過對殘差序列進行修正,使預測值滿足預測精度,為進行客觀事物的預測工作帶來了極大的便利。
1 預測模型構建原理
1.1 灰色模型原理
GM(1,1)是基于單變量一階常微分方程建立的,被稱為一階一元灰色方程,是最普遍使用的一種灰色模型。
假設初始數據序列x(0)={x(0)(1),x(0)(2),…,x(0)(N)},令x(1)(i)=,此式所表示的數據序列為初始數據序列的一次累加而得到,可稱為一次累加生成。顯然有x(1)(1)=x(0)(1) 。初始數據序列按一次累加生成得出:
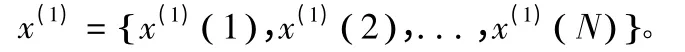
設x(1)符合一階常微分方程:
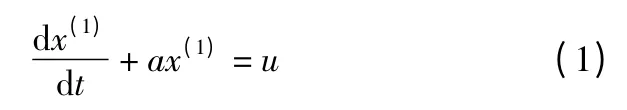
式中,a 和u 是常數,a 是發展灰數;u 是內生控制灰數,是對系統的常定輸入。
此方程符合初始條件:t=t0時x(1)=x(1)( t0)的解為:
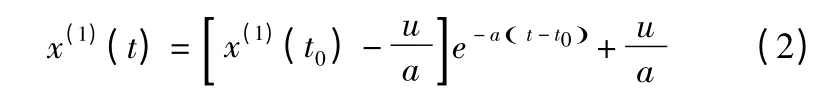
對等間隔取樣的離散值(t0=1)則為:
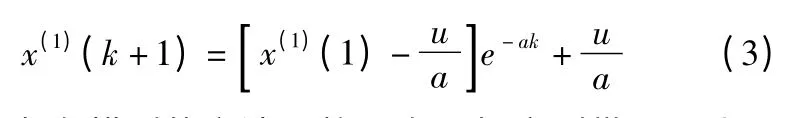
構建灰色模型的方法是將一次累加序列帶入最小二乘法來求得常數a、u。
因x(1)(1) 為初值,故將x(1)(2),x(1)(3),…,x(1)(N),分別代入式(1),用差分代替微分,又等間隔取樣,△t=(t+1)-t=1,故得:
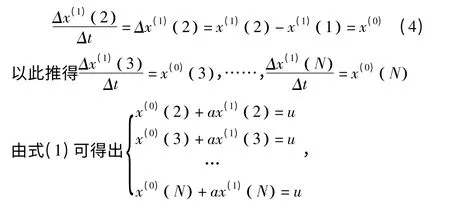
移項后轉化為向量的數量積形式:
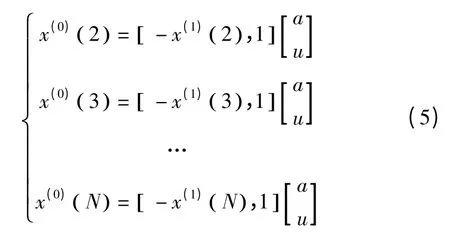
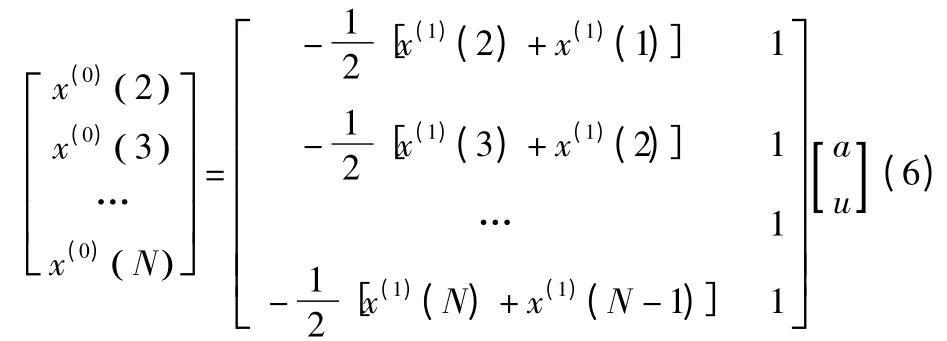
令y=(x(0)(2),x(0)(3),...,x(0)(N))T.T 表 示轉置。
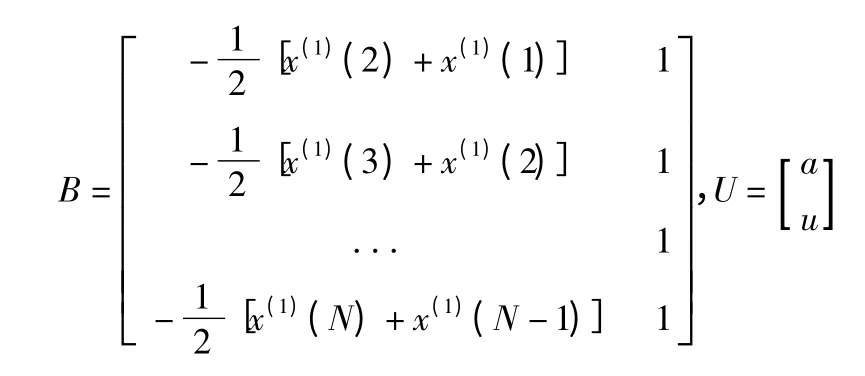
則式(6)可表示為矩陣形式:

式(7)的最小二乘估計為:
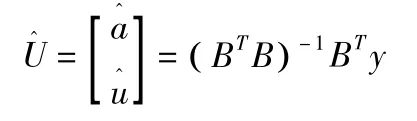
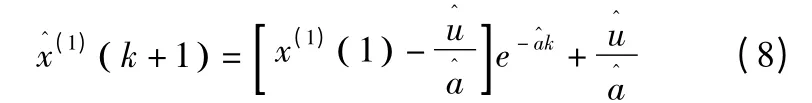
此方程為時間響應方程。
最后得到預測模型:
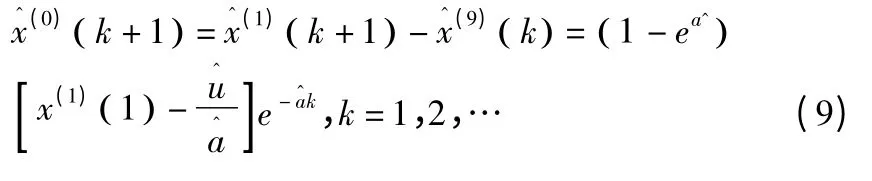
1.2 灰色殘差模型原理
由灰色GM(1,1)模型計算出的模擬值與初始數據有較大差異時,即誤差(或殘差)較大時,可將殘差序列建模,獲得滿意的殘差序列,之后將修正后的殘差模型來帶入到所求得的灰色GM(1,1)模型,這種融合了殘差模型及灰色GM(1,1)模型的新模型稱為灰色殘差模型。
將初始數據序列x(0)中代入時間響應方程,求得序列(j),j=i,i+1,……,n。可求得殘差 序列e(0)={e(0)(i),e(0)(i +1),…,e(0)(n)},經一次累加生成可求得序列e(1)={e(1)(i),e(1)(i +1),…,e(1)(n)},按照灰色預測建模步驟,可求得殘差序列的響應方程進行求導可得,得殘差修正后的模型為:
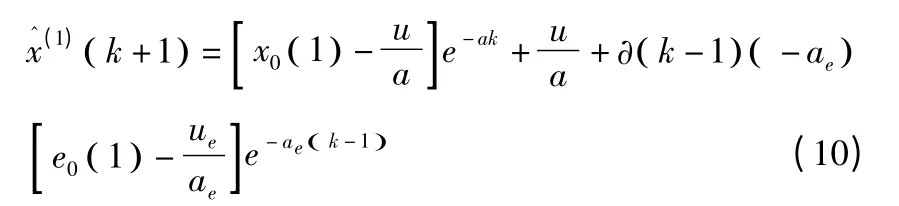
最終可求得經殘差修正后的預測模型:
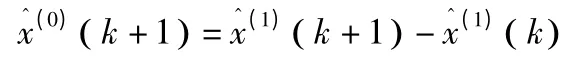
注:殘差序列e(0)中數據必須為非負數,如果有負數存在,可進行非負處理[8],如本文選取,將其加到殘差序列e(0)的各項中。
2 精度檢驗
精度檢驗包括殘差檢驗與后驗差檢驗,檢驗精度標準一般以后驗差檢驗指標中的后驗差比值C、小誤差概率P作為評定指標。
2.1 殘差檢驗
殘差:E (k)=x(0)(k)-x^(0)(k),k=2,3,…,N
相對殘差:
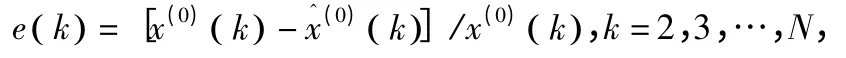
2.2 后驗差檢驗

2.3 檢驗精度標準
后驗差比值C 越接近0,小誤差概率P 越接近1,預測精度越高,檢驗精度標準見表1。

表1 檢驗精度標準
3 南通市工業需水量預測
對南通市1998—2012 年農業用水量進行分析核實的如表2 資料(以下單位均為億m3)。
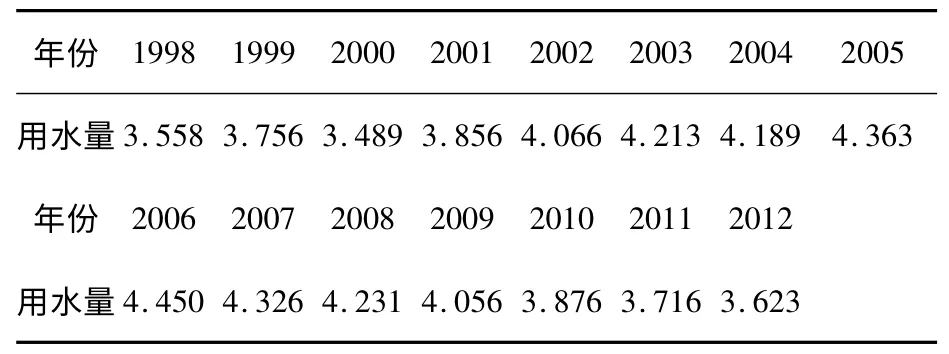
表2 南通市工業需水量1998~2012 年統計數據
3.1 建立灰色預測模型
以1998~2012 年工業用水量數據作為原始序列x(0),經一次累加生成x(1),由式(6)可求得B 和y,用最小二乘估計求出,可得時間相應方程:
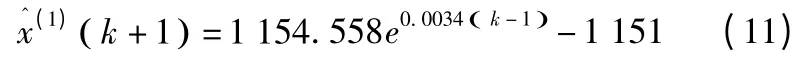
由后減還原可得預測值模型為:
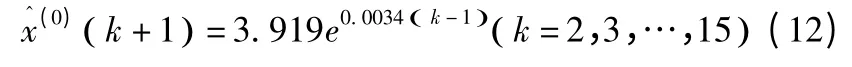
依據式(12)計算得到1999 年~2012 年的用水量模擬值見表3。
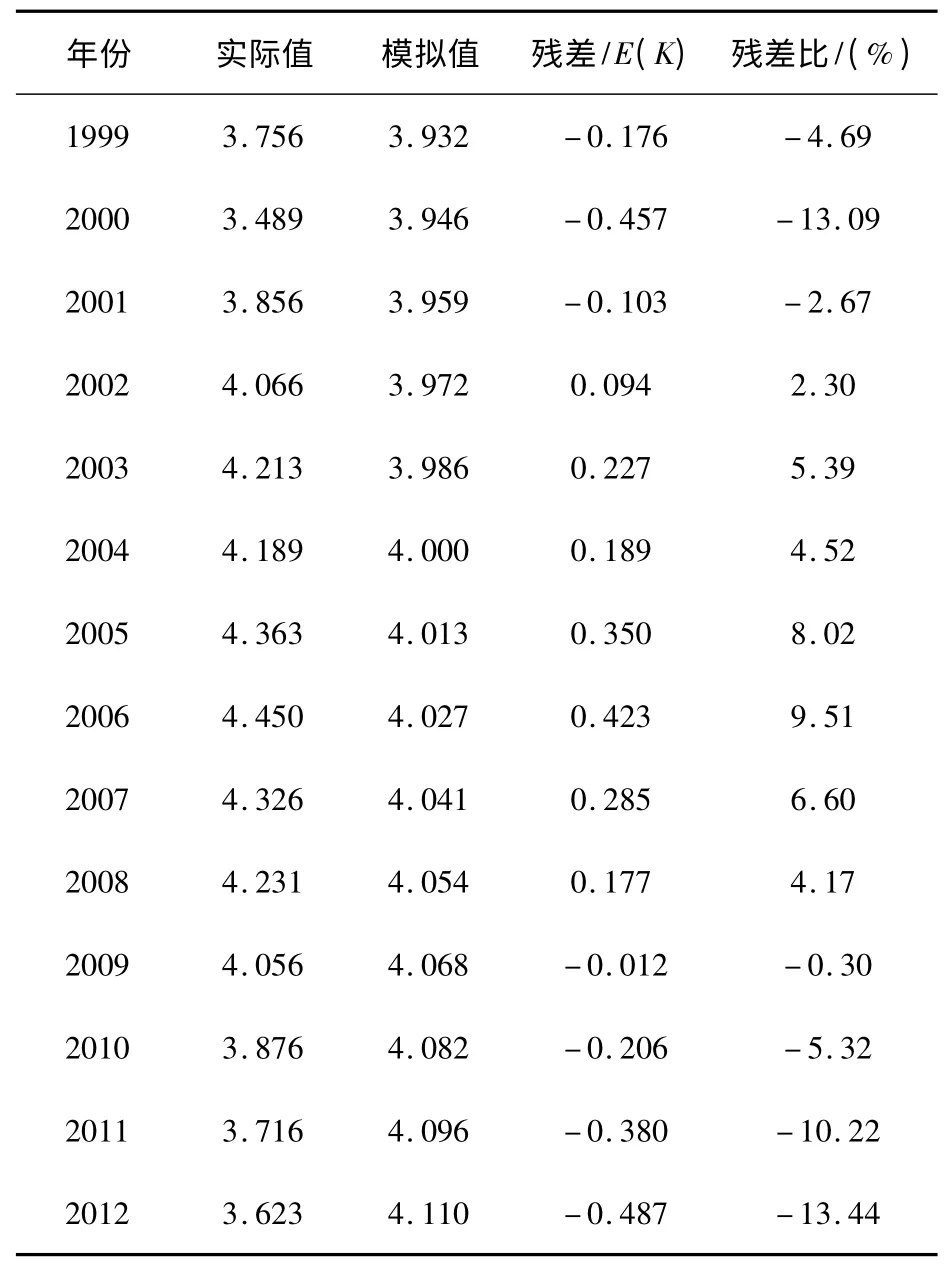
表3 GM(1,1)模型預測及精度分析
將表2 中數據帶入精度檢驗公式,得P=0.57,C=0.968,檢驗精度等級為“不合格”,未達到預測精度要求,故不能進行南通市未來年份工業用水量預測。
3.2 建立灰色殘差預測模型
建立灰色殘差模型,首先選擇殘差序列e(0)中的尾端的7個數據作為原始數據,即{0.423,0.285,0.177,-0.012,-0.206,-0.380,-0.487},由于殘差序列中存在負數,故應做非負處理,處理之后的序列經一次累加生成x(1),由式(6)可求得B 和y,用最小二乘估計求出,可得殘差序列的時間相應方程:
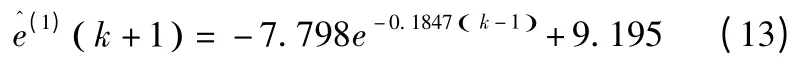
由后減還原得修正后的殘差值:
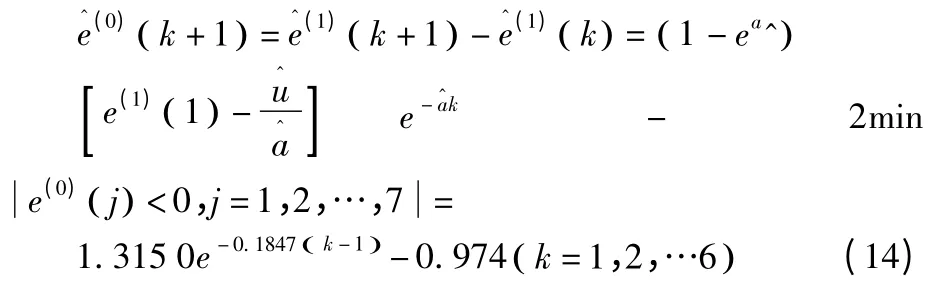
將式(12)和式(14)帶入到式(10)中,最終得到灰色殘差修正模型下的預測值:
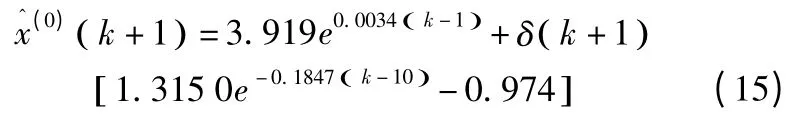
由殘差模型模擬出的2006—2012 年這7 年數據通過精度檢驗,可得P=1,C=0.152。檢驗精度等級為“好”,所以灰色殘差模型可作為南通市工業需水量預測模型。通過式(15)計算得南通市未來5 年內工業需水量見表4。
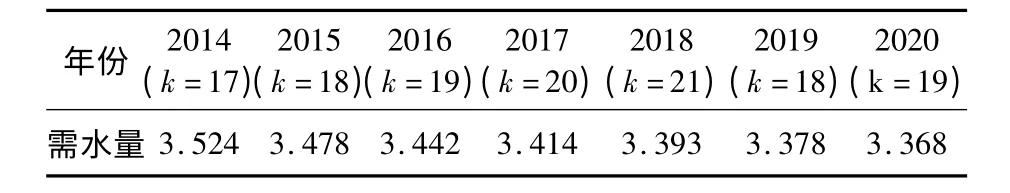
表4 灰色殘差模型預測2014—2020 年南通市工業需水量
4 結果分析
灰色殘差模型采用的數據是2006—2012 年南通市工業需水量,由于2006 年數據留作初值,故選取其余6 年的模型下的模擬值及其檢驗精度與灰色模型做分析比較,分析結果見表5,表6。
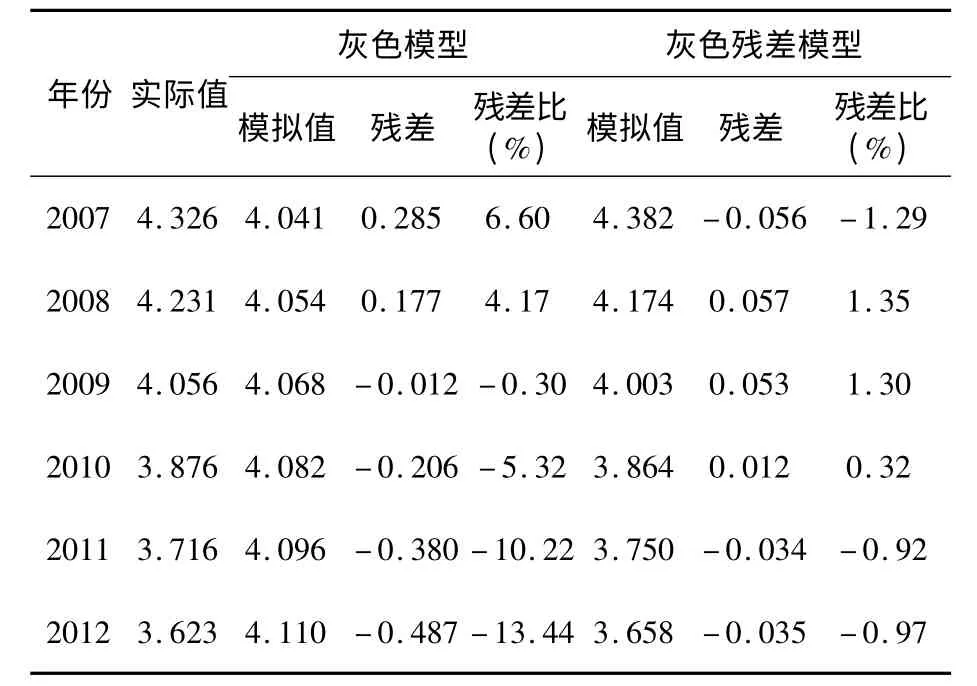
表5 兩種模型下預測值與誤差分析比較
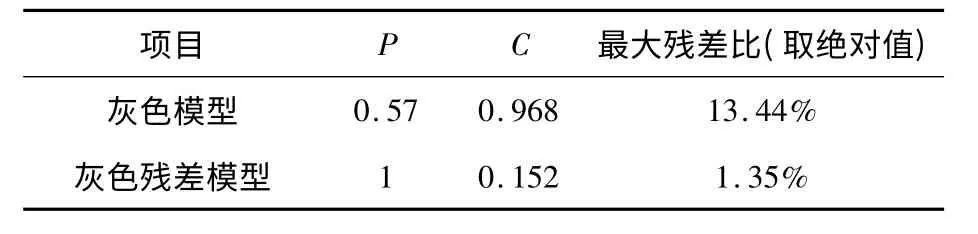
表6 預測精度對比
從上述比較中可看出,灰色殘差模型的各項預測精度指標均優于灰色模型,其預測精度等級為“好”,而灰色模型預測精度等級為“差”。
5 結論
1)工業需水量受工業產值、產品結構、工業用水重復利用率、工業用水價格、工業技術進步指數、政策性節水率、中水回用情況以及時間等因素的制約[9-10],變化較為復雜。因此,要想將所有影響因素一一羅列出來,并給出這些因素與需水量之間準確的函數關系十分困難[11]。而灰色模型預測出的需水量是呈指數變化的,總趨勢單調上升或下降,故此灰色模型中出現較大的殘差。
2)即使在原始數據變化較大的情況下,灰色殘差模型還是顯著地減小了灰色模型下的模擬值和實際值之間的殘差,使灰色模型達到滿意的預測標準,所以灰色殘差模型的適用范圍要更廣。但有時灰色殘差總不一定將能誤差減小到理想的范圍內,滿足預測精度標準,故現在出現了很多組合模型[12]結合了灰色等維遞補理論[13]或灰元[14]理論等,以其各自的特點來相互彌補各自的不足,同時配合殘差模型減小殘差,以求滿足預測精度。可以說灰色殘差模型的出現為灰色模型的應用提供了更廣闊的空間。總之,灰色殘差需水量預測模型為今后城市水資源綜合規劃和供水計劃的制定提供了極大的幫助。
[1]席洋,程水源,郭秀銳,等.灰色預測模型在城市需水量預測中的應用[J].環保科技,2007,13(1):25-29.
[2]張雅君,劉全勝.需水量預測方法的評析與擇優[J].中國給水排水,2001,17(7):27-29.
[3]楊建飛,劉俊民,陳琳.基于灰色殘差模型的灌區地下水最小埋深預測[J].人民黃河,2011,33(7):101-105.
[4]傅金祥,潘海賓,馬興冠.灰色殘差模型與遞補模型對比及在城市需水量預測中的應用[J].給水排水,2008,34(6):111-113.
[5]劉躍辰,王秋兵,錢鳳魁,等.灰色模型與回歸模型在農用地基準地價評估中的比較分析[J].農業工程學報,2010,26(Supp2):344-348.
[6]鄧聚龍.灰色預測與決策[M].武漢:華中理工大學出版社,1991.
[7]崔延松,魯紅衛,曹陽,等.貴州省工業需水量預測研究[J].中國水利,2014(6):31-33.
[8]李剛,黃同愿,閆河,等.公路交通預測的灰色殘差模型[J].交通運輸工程學報,2009,9(5):88-93.
[9]汪妮,孫博,張剛.改進的灰色模型在城市工業需水量預測中的應用[J].西北大學學報:自然科學版,2009,39(2):313-316.
[10]張雅君,劉全勝.北京工業需水量的多元回歸分析及預測[J].給水排水,2002,28 (11):53-55.
[11]王兵,王伯鐸,林積泉,等.高等學校污水再生利用的途徑與效益研究[J].西北大學學報:自然科學版,2007,37 (2):322-325.
[12]梁學玉,張鑫,孫天青.組合灰色預測模型在城市用水量預測中的應用[J].人民黃河,2010,32(4):79-80.
[13]胡德秀,楊杰.城市需水量的灰色非線性預測[J].陜西水力發電,1999,15(1):23-27.
[14]周振祥,周芳,等.維灰色遞補模型在GDP 預測中的應用[J].黃岡師范學院學報,2011,6(31):27-28.

